Rethinking 3D-QSAR

Abstract

The average error of pIC50 prediction reported for 140 structures in make-and-test applications of topomer CoMFA by four discovery organizations is 0.5. This remarkable accuracy can be understood to result from a topomer pose’s goal of generating field differences only at lattice intersections adjacent to intended structural change.

The purpose of 3D-QSAR, as of all industrial CADD activities, should be to provide guidance that furthers drug discovery, usually as quantitative predictions of the biologically critical properties of individual structures. Should it not follow that a new methodology providing surprisingly superior accuracy for such predictions deserves thoughtful consideration? Particularly in view of the many recent publications [1–8] whose very titles express substantial pessimism about many common practices and even the fundamental principle of QSAR?

Initial outcomes of topomer CoMFA trials

Results from each of the first seven “real world” make-and-test applications of topomer CoMFA, each undoubtedly prospective, have all been reported as “successful”. However, “success” is a somewhat vague and subjective outcome. As a starting criterion, there should be potency forecasts for multiple structures from the “successful model”, to minimize concern about chance agreement between prediction and result and to improve the sampling of prediction errors. Furthermore, since the purpose of CADD is to further drug discovery, another useful “success” is to identify the structures that are most likely to progress a current “best candidate” into the desired single compound satisfying all pre-clinical requirements. However, success in the discovery project itself, generation of a clinically promising drug candidate, remains much too dependent on unpredictable biological outcomes to be a more than anecdotal indicator of a “successful” CADD application.

A further challenge to the broader CADD community in assessing a claim of model “success” is that the structures and biological properties, either from which the model was derived or for which the successful predictions were made, are almost always made confidential by the guardians of intellectual property, at least for many years and often until any impetus sufficient to publish has vanished. An alternative possibility, though, is to obtain the model performance statistics themselves, in this instance for four of the seven reported topomer CoMFA successes. Their results appear in Table 1, where each of the four rows provides such statistics for a model from a different discovery organization (one biotech, two full-sized and one mid-size pharma).

Table 1.

Outcomes of make-and-test applications of topomer CoMFA by four discovery organizations

Ref.	TopCoMFA model properties					Make-&-test outcomes
	q2	SD	# Comp	N	pIC50 range	# Predicted	pIC50 SDEP	N top pIC50 quartile
[9]	0.220	0.66	3	122	3.3–7.3	7	0.54	2
[10]	0.593	0.49	8	270	4.2–8.8	2	0.36	2
[11]	0.518	0.63	5	358	NA	44	0.69	Most
NA	0.342	0.95	7	206	4.3–8.0	87	0.48	19
Total/Average						140	0.51

See text for explanation

The most important results may be found in its right hand block labeled “Make-&-Test Outcomes”. Particularly remarkable is the very low error of pIC50 prediction for the four biological properties of greatest interest, slightly greater than 0.5 whether averaged over the four distinct models or over the total of 140 predictions. This error value is furthermore consistent with an average pIC50 prospective prediction error of 0.6 for 148 structures predicted from 12 independent models, as previously reported [12]. An overall average prediction error of less than 0.6 over 288 structures and 16 models, including a standard deviation of 0.2 among those 16 independent error values, would seem rather substantive evidence for an extraordinary accuracy of pIC50 predictions that topomer CoMFA models yield, an accuracy which to the best of my knowledge is quite unprecedented. (As one point of comparison, it may be recalled that the rule-of-thumb value for the uncertainty of a measured pIC50 value is around 0.3.)

Also apparently unprecedented, though less reliably so, is the complete absence so far of any reported “unsuccessful” make-and-test applications of topomer CoMFA. Although common sense dictates that this perfect “success” record among the seven trials reported will not long continue, application of probability theory to these initial outcomes does allow some assessment of the likelihood that a next trial will also experience “success”. If this likelihood of success is actually 50%, the probability of observing four successes in the first four trials would be 0.5^4, or 0.0625, a value whose similarity to the conventional “95% confidence limit” supports expectation of at least a “50:50 chance” of success in a next trial. If the other three “successes” are also accredited, then the 95% criterion yields a lower bound to the true likelihood of success in the next trial as about 2/3, or “2–1”.

Performance with respect to the other above-proposed success criterion, the counts of the predictions that flagged the structures most likely to further project goals, taken here specifically as those having a pIC50 within (or better than) the most desirable quartile of the pIC50 range so far observed experimentally (in the right-most column of Table 1), also seems acceptable. Reportedly one of these application outcomes played a critical role in identifying a drug candidate that is now being licensed commercially, and two of the others significantly influenced their projects’ future strategies.

Those statistical modelers who emphasize q² magnitudes might have been discouraged by several of the q² values for the model derivations themselves, in the left-most column of Table 1. However, the values in the adjacent SD column suggest that one cause is a modest range of pIC50 values within several training sets, with their pIC50 prediction accuracies nonetheless seeming entirely satisfactory. Another factor leading to structurally conservative predictions (those most likely to produce the smallest errors of prediction) is sociological. The CADD scientist may have wisely included the widest possible structural variation in his training set, tending to lower the q² of the model. However when the model is applied to predictions in the “real world” context of a drug discovery project, make-and-test recommendations will seek to maximize the confidence of a synthetic chemist, who will usually be considering many other structural candidates for the investment of his bench resources.

Topomer CoMFA methodology

Essentially “topomer CoMFA” is conventional CoMFA using topomers as the alignments. A topomer, then, is defined [13] as a molecular fragment having a single internal geometry or “pose” (conformation plus position). The underlined words highlight the two means by which the topomer methodologies produce high shape compatibilities. By definition, a molecular fragment possesses at least one open valence, so a topomer is positioned in space, or “rooted”, simply by superimposing its open valence onto a fixed Cartesian vector. The single conformation of a topomer is determined only by its own topology (“2D” structure), and not by either direct comparison with other structures or intramolecular energy. Yet the overall goal is that similar fragment topologies should afford similarly shaped topomers. Thus, topomer valence geometries are generated by a 3D-model builder such as Concord, followed by canonically-determined adjustments to acyclic single bond torsions, stereochemistries, and ring “puckerings”. Topomer CoMFA simply uses topomers from the fragmented training set as the 3D-QSAR-requisite aligned input structures, and otherwise differs from “standard CoMFA” only in its use of multiple “CoMFA columns”, one for each set of fragments (aka “R-groups”). Since all of the steps in topomer generation are automatic and user inaccessible, a topomer CoMFA prediction is almost entirely objective, depending only on the 2D connectivity’s, user-specified fragmentations, and measured biological potencies of the training set structures.

Reconsidering 3D-QSAR

How can topomer CoMFA’s pIC50 predictions be so exceptionally accurate? Obviously it’s not a consequence of allegiance to the most frequent goal when assembling ligand descriptions for CADD analysis, maximum fidelity to any direct and presumably relevant experimental observables. Instead, a topomer conformation may for example even include so dismaying a physicochemical heresy as sterically overlapping atoms. There must exist some other causative factor for topomer CoMFA’s remarkable performance, such as the following reconsideration of 3D-QSAR now proposes.

To begin, it is recommended that the interested reader consciously tries to set aside her or his mental models of QSAR processes. Let us agree only that the goal in QSAR is to seek combinations of interpretable chemical structure descriptors whose differences afford sufficiently powerful and consistent models of differences in the biological response(s) of interest (as typically inferred from q²) to be of value in guiding decision making.

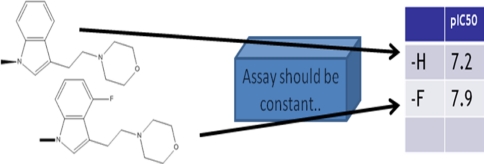
Figure 1 shows the simplest possible excerpt from a (fictitious) structure–activity table. What is the cause, the only possible cause assuming the biological assay to be reproducible, of the only observable response difference within this table excerpt, between a pIC50 of 7.2 and one of 7.9? Right—it’s the replacement of –H by –F. Assuredly the pIC50 change resulting from even such a simple replacement of one atom by another may have been mediated by some profound reorganization of the geometry of ligand-to-target bindings. Nevertheless the only cause of such a hypothetical reorganization would remain—the replacement of –H by –F. Admittedly such profound reorganizations might then yield a series of pIC50 observations whose differences have no discernable or consistent relationship to differences in their associated structural descriptors. However that circumstance should be revealed simply by tne lack of any model having acceptable q² values.

Fig. 1.

Generation of a very simple excerpt from an imaginary QSAR input table

In 3D-QSAR, the “interpretable chemical structure descriptors” are of course the ligand field values at pre-specified grid intersections. Here follows the most critical element of this reconsideration of 3D-QSAR. The differences among these ligand field values arise for only two distinct classes of reasons:

1. The direct and relatively unambiguous effects of the intentional changes to the ligand structures themselves. In the example of Fig. 1, the replacement of –H by –F would have an almost negligible effect on the local steric field, but a substantial effect on the electrostatic field. Of particular importance, these direct and unambiguous effects of an –H for –F change are extremely local, probably insignificant at more than a half-dozen lattice intersections (though the differential effects of –H and –F on partial charges elsewhere in the ligand might slightly complicate this particular example).

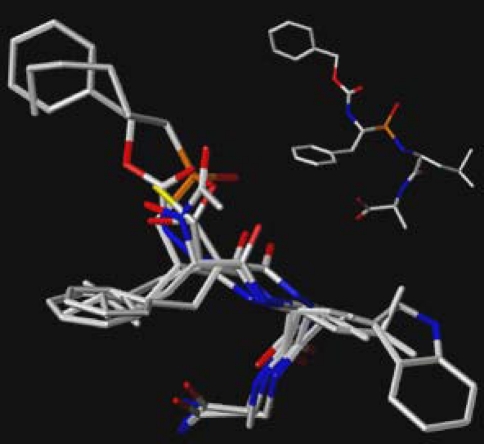
2. The indirect and relatively uncertain effects of this –H to –F difference between ligand structures on the geometries of their binding to the target. Of particular importance, even modest changes in the relative geometries of binding to target will affect the ligand field values at dozens or even hundreds of lattice intersections. Figure 2 shows one example of this phenomenon. A small combinatorial library, whose structures differ from one another only in a few atoms at each of their two ends, was docked into a target, the target then being removed. Evidently the peripheral structural differences after docking generated somewhat different locations for the actually identical atoms of the library’s constant core structure. As shown, even these slight differences in core atom locations generated substantial differences in the ligand fields at almost all the surrounding lattice intersections, differences which even if real can at most be the secondary causes (e.g., not the “first movers” of Aristotelian and medieval philosophy) of the differences in the biological properties of interest.

Fig. 2.

Example of the pose variations among structurally constant atoms that docking of structures varying only in their terminal groups can produce

So the reader will hopefully agree to this distinction between two fundamental causes of differences among the ligand field values that are the structural descriptors in 3D-QSAR—the primary, direct, and spatially relatively localized effects of the certain changes to the ligand structures themselves, contrasted with the secondary, relatively uncertain, and spatially quite diffuse effects of any resulting changes, even if modest, to the geometries of ligand-to-target binding.

Now, please recall a fundamental difference in the behavior of 3D-QSAR’s foundational statistical methodology PLS (partial least squares) from that of the far more familiar MLR (multiple linear regression). To detect relationships between differences in structural and biological properties, MLR is allowed to manipulate (scale and rotate) individual columns of structural properties, but PLS may only manipulate (scale and rotate) the entire block of structural properties. The adverse consequences of MLR’s individual column manipulations—chance correlation—are widely recognized. The adverse consequence of PLS’s restriction to manipulation of the entire descriptor block are not so well-known. With PLS, even a perfect correlation with the biological property that exists with only a few columns within the descriptor block may remain altogether hidden, because of the “inertia” of the other uncorrelated descriptors [14].

So 3D-QSAR relies on a statistical methodology which is insensitive to correlations involving only a few descriptor columns to analyze a descriptor matrix of ligand field values whose most direct, certain, and causative differences tend to be highly localized to a few columns. To the extent that field variation resulting from indirect, uncertain, and at most secondarily causative differences in ligand-to-target binding geometries competes, the effects of these direct, certain, and causative differences might even remain entirely undetected.

Although the topomer alignment protocol was developed with quite different applications in mind, it turns out that their consequences when applied to 3D-QSAR are ligand (fragment) poses that minimize the indirect and uncertain effects of any differences in ligand-to-target binding geometries. Topomer alignments are intended to generate differences in ligand field values only where those differences are directly caused by changes to ligand structures. Elsewhere their goal is to produce geometrical identities from structural identities and geometric similarities from structural similarities.

Discussion and summary

The remarkably successful outcomes of the initial make-and-test applications of topomer CoMFA models, rather than being mysterious, thus seem a straightforward consequence of how the topomer poses focus a PLS model onto the most assuredly controllable class of field differences, making its proposals for structural modification particularly likely to be productive. While the topomer poses also provide significant advantages in convenience, speed, objectivity, and functional versatility [15], any other 3D-QSAR methodologies that restrict field variations to the most direct effects of ligand structure variations should also tend to yield more successful predictions. (However, to minimize the risk of chance correlations, such restrictions should only be applied a priori, before any PLS modeling, rather than by some sort of iteration between PLS modeling and field manipulations.)

This reconsideration also may address several other long-standing surprises about the behaviors of 3D-QSAR and other CADD methodologies, such as:

• The superior statistical qualities of 3D-QSAR models based on poses that superimpose presumably critical ligand features, rather than docked conformations [16];

• The at best modest improvements in statistical quality afforded by greater accuracies in field calculations, such as finer grid resolution or improved atomic charges;

• The superiority of similarities among “2D descriptors” (such as the Tanimoto coefficients of fingerprints) in predicting biological similarities [17], compared to similarities among 3D similarities (as PLS is probably not the only analytical methodology that is seriously distracted by irrelevant variation among candidate descriptors).