Modular analysis of the probabilistic genetic interaction network

Abstract

Motivation: Epistatic Miniarray Profiles (EMAP) has enabled the mapping of large-scale genetic interaction networks; however, the quantitative information gained from EMAP cannot be fully exploited since the data are usually interpreted as a discrete network based on an arbitrary hard threshold. To address such limitations, we adopted a mixture modeling procedure to construct a probabilistic genetic interaction network and then implemented a Bayesian approach to identify densely interacting modules in the probabilistic network.

Results: Mixture modeling has been demonstrated as an effective soft-threshold technique of EMAP measures. The Bayesian approach was applied to an EMAP dataset studying the early secretory pathway in Saccharomyces cerevisiae. Twenty-seven modules were identified, and 14 of those were enriched by gold standard functional gene sets. We also conducted a detailed comparison with state-of-the-art algorithms, hierarchical cluster and Markov clustering. The experimental results show that the Bayesian approach outperforms others in efficiently recovering biologically significant modules.

Contact: dengmh@pku.edu.cn; fangtingli@pku.edu.cn; zhuyp@hupo.org.cn

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

With the recent advances in high-throughput technologies, researchers can now acquire data on molecular networks with unprecedented speed. As a result, enormous insight is gained with respect to cellular functions at a systems level (Costanzo et al., 2010; Lee et al., 2004; Uetz et al., 2000). Computational methodologies have been developed to analyze data and extract information on molecular networks, such as protein interaction networks (Collins et al., 2007a; Shachar et al., 2008; Sharan et al., 2005a, b; Yosef et al., 2009), transcriptional regulatory networks (Lee et al., 2002) and genetic interaction networks (Bandyopadhyay et al., 2008; Costanzo et al., 2010; Kelley and Ideker, 2005; Schuldiner et al., 2005).

Genetic interactions refer to the phenomenon whereby the mutation of one gene affects the phenotype associated with the mutation of another gene. In budding yeast, such interactions can be measured on a genome-wide scale (Collins et al., 2007b; Fiedler et al., 2009; Schuldiner et al., 2005; Wilmes et al., 2008) using the Epistatic Miniarray Profile (EMAP) platform. In EMAP, double deletion strains are systematically constructed by crossing a query strain, which carries a mutation of one gene, with a library of test strains, each one carrying a mutation of a second gene. The double mutant strains of different query genes are grown on plates for a predetermined period of time. Then the colony size of the double mutant strains is measured, and the extent to which a specific double mutation deviates from other double mutation strains of the same query gene is derived. Generally, one can assign an S score to each pair of genes. While a negative S score indicates a synthetic sick/lethal interaction, a positive S score indicates an alleviating interaction (Collins et al., 2006). So far, several studies have been carried out in Saccharomyces cerevisiae (Collins et al., 2007b; Fiedler et al., 2009; Schuldiner et al., 2005; Wilmes et al., 2008) and S.pombe (Roguev et al., 2008). These large-scale datasets shed light on cellular organization and gene functions, and they are especially effective in revealing protein complexes and modules participating in common pathways.

EMAP studies generally benefit from the following: (i) genome-scale study makes it possible to evaluate the extent of similarity between the genetic interaction profiles of two genes in an unbiased manner. (ii) Quantitative output makes it possible to detect subtle interactions. Current approaches in analyzing EMAP data often choose an arbitrary cutoff to determine whether an EMAP measure indicates a genetic interaction (Fiedler et al., 2009) and thus outputs a binary genetic interaction network. Hierarchical cluster analysis is another methodology commonly used in analyzing EMAP data, using the correlation between genetic interaction profiles as a measure of functional association. Cluster analysis has been proven efficient in predicting biological pathways and protein complexes (Schuldiner et al., 2005). Nevertheless, assigning a hard threshold loses too much EMAP quantitative information, while the simple clustering method, although effective for the most dominant pathways and protein complexes, is too stringent for pathways of moderate phenotypic effect.

Cellular functions and processes are carried out in a series of interacting events, and genes participating in the same biological process tend to interact with each other. Therefore, identifying gene modules composed of densely interacting gene sets is of great interest. Computational approaches predicting modules in physical protein interaction (PPI) networks have been successful in revealing biological pathways and protein complexes (Brohee et al., 2006; Scott et al., 2006; Sharan et al., 2005a, b). However, the current methodologies in analyzing genetic interaction networks do not efficiently address the important issue of module identification.

With the goal of identifying modules in genetic interaction networks, we extended the Bayesian method (Sharan et al., 2005a, b) to genetic interaction networks. This framework has already been demonstrated as an efficient algorithm to identify modules in PPI networks. However, the major difficulty in applying it to EMAP lies in the lack of a probabilistic score assigned to each interaction. To solve this problem, we applied a Gaussian mixture distribution to model the distribution of EMAP output, and, as a result, each interaction is weighted by posterior probability. We also conducted a detailed evaluation of our method, comparing it with gold standard functional gene sets. In addition, we compare our method with other state-of-the-art algorithms, including hierarchical cluster (HC) analysis (Collins et al., 2006) and Markov Clustering (MCL) (van Dongen et al., 2000). The experimental results show that our method recovers functional gene sets, and significantly outperforms the other two algorithms.

In addition to identifying modules in the genetic interaction network, another major contribution of our work is the use of a mixture model. Instead of arbitrarily choosing a threshold, the mixture model uses a soft threshold, which takes advantage of the quantitative nature of EMAP data to make further inference. The framework of mapping EMAP output into a probabilistic genetic interaction network through mixture modeling and identifying modules in the derived network can be easily applied to other EMAP datasets.

2 MATERIALS AND METHODS

2.1 Materials

The test datasets in this study are EMAP profiles of the early secretory pathway (ESP) (Schuldiner et al., 2005) and phosphorylation network (Fiedler et al., 2009) of the budding yeast. The ESP dataset consists of 424 genes with about 80 000 genetic interaction measurements. The phosphorylation dataset consists of 483 genes, with about 100 000 genetic interactions measurements.

For the ESP EMAP dataset, gold standard functional gene sets are defined by GO terms (Ashburner et al., 2000), KEGG pathways (Kanehisa and Goto, 2000) and MIPS protein complexes (Mewes et al., 2008).

For the phosphorylation EMAP dataset, a benchmark dataset with true genetic interactions is defined by merging interactions from the following two sources:

• Phosphorylation datasets from the literature, including kinase-substrate and phosphatase-substrate gene pairs and kinase-kinase, kinase-phosphatase and phosphatase-phosphatase gene pairs that share common substrates (Fiedler et al., 2009);

• MIPS small-scale interaction datasets (Mewes et al., 2008).

The MIPS small-scale interaction datasets are included in order to form an unbiased benchmark dataset. The numbers of interactions in each dataset are listed in Supplementary Table S1.

2.2 The Bayesian approach to identify modules

Given an interaction network in which the interaction of every two genes is weighted by a probability (see Section 2.3), the goal of our method is to identify modules in such network. The problem is formulated as follows (see Supplementary Table S6 for the notation table).

Let V be a set of genes, and genes in the set are denoted as lower case letters. Assume that genes in a module interact in pairs and that such interactions are independent of each other. Given that V is a module, the likelihood of the observed S scores in V is defined (Equation 1).

(1)

Applying the law of total probability, the probability of observing an interaction with score S_ab in a module, P(S_ab | Module) , can be derived (Equation 2), where T_ab means that interaction (a, b) truly exists, while F_ab means the opposite. The distribution of S scores only depends on whether or not an interaction is true (Equation 3). Thus, P(S_ab | Module) is simplified to Equation 4.

(2)

(3)

(4)

Since genes in a module are functionally related, they are likely to interact in the genetic interaction network. In another word, the probability that the interaction (a, b) exist when a and b belong to the same module, P(T_ab | Module), should be large. P(T_ab | Module) is set to 0.95 in our method.

As a background model, we assume a gene set V is sampled in a random network. A two-step sampling procedure is used to randomize the interaction network:

1. Choose a gene a with the probability 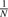, where N is the number of genes in the network;

2. Choose a second gene b with the probability proportional to the rank of P(T_ab | S_ab) in P(T_a· | S_a·) in descending order, and add (a, b) to the interaction network. P(T_a· | S_a·) is the probabilistic genetic interaction profile of gene a.

According to the network sampling procedure, the probability that (a, b) exists in the random network, P(T_ab | Background), is proportional to i_ab + i_ba. i_ab is the rank of P(T_ab | S_ab) in P(T_a· | S_a·), and i_ba is the rank of P(T_ab | S_ab) in P(T_·b | S_·b).

The background model has two desired properties: (i) when (a, b) and (c, d) have the same S score, the pair with lower rank in their corresponding profiles is assigned a greater chance of appearing in the random network. (ii) The distribution of the posterior probabilities of each gene in the random network is kept consistent with the observed network. The likelihood is similarly defined (Equation 5, Equation 6; B = Background).

(5)

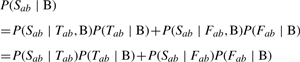(6)

The likelihood ratio of ‘Module’ and ‘Background’ can be computed by summing over all pair-wise interactions in the module (Equation 7). It can be computed if P(S_ab | T_ab) and P(S_ab | F_ab) are known (see Supplementary Method 1), which are derived from mixture modeling (see Section 2.3).

(7)

2.3 Mixture model

Genetic interaction between a pair of genes can be classified as positive, negative and non-interacting. Therefore, the S scores in an EMAP experiment are a mixture of three subpopulations: positive genetic interactions (S₊), negative genetic interactions (S₋) and null interactions (S₀). Assuming that each subpopulation is a Gaussian distribution, the Gaussian mixture model is applied to characterize the distribution of the S scores in an experiment (Equation 8).

(8)

α₋, α₀ and α₊ are the proportions of gene pairs of the particular interacting type, and S_* follows Gaussian distribution (Equation 9).

(9)

The parameters can be estimated through the EM algorithm. The posterior probability that a pair of genes with S score s has a true negative or positive genetic interaction can be derived (Equation 10).

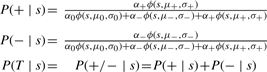(10)

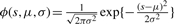, which is the Gaussian density function.

2.4 Prediction of positive triplet motifs

To demonstrate the advantage of the posterior probability over S score, both scores are applied to predict triplet motifs, and the results are compared. As the simplest motifs in a genetic interaction network, triplet motifs with three positive interactions tend to display genes that function in a series (Fiedler et al., 2009). Fiedler et al. scored such a triplet with the product of the S scores of each pair of genes (Equation 11).

(11)

To score a positive triplet motif composed of genes a, b and c, the sum of the log posterior probabilities of each pair of genes is used (Equation 12), assuming that interactions are independent of each other.

(12)

All triplets with three positive S scores are scored, and the precision of the two methods are compared (Equations 11 and 12). For each method, we took the top-k triplets, and the precision is defined as the proportion of true interactions in all interactions in top-k triplets. An interaction is regarded as a true interaction if it is present in the benchmark dataset (see Section 2).

2.5 Module-grown algorithm: a heuristic optimization of the log likelihood ratio

The goal is to identify modules that have the largest log likelihood ratio. However, the searching space is prohibitively large. Instead, the log likelihood ratio is optimized heuristically. Since modules must contain dense submodules, we first identified all four-cliques in a degenerated binary interaction network. Next, these four-cliques are greedily expanded to modules with moderate size.

First, we defined a threshold T as the 5% upper quantile of the log likelihood ratio of all edges in the genetic interaction network. The edges whose log likelihood ratio does not pass the threshold are deleted. Next, party nodes, with a degree no less than 50 in the derived discrete network, were deleted from the network. In the resulting network, there are 168 four-cliques, and these four-cliques are used as seeds to identify modules. Then, the four-cliques are expanded into a module in a forward procedure. At each iteration, the gene that adds the largest likelihood ratio to the current module is selected as a candidate member. If the average log likelihood ratio (ALLR) that the candidate gene adds is above the predefined threshold T, the gene is appended to the module. The iteration stops if no genes can pass the threshold or the module reaches the maximal size M. We set M to 10 in the current study. Finally, 168 modules are predicted in the ESP dataset.

2.6 Remove redundancy in predicted modules

A rough inspection revealed that many genes are present in multiple modules, thus causing redundancy in our prediction. We removed the redundancy through a merging approach.

1. Initial: suppose we have K modules.

2. Iteration: compute the ALLR (Equation 13) achieved by merging each two modules that share at least one gene. Then, merge the two modules that have the largest ALLR if the corresponding ALLR passes the threshold.

3. Termination: the iteration terminates if no genes are shared across modules, or the ALLR of merging any two modules is less than T.

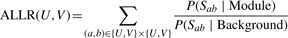
   (13)

2.7 Enrichment analysis

The enrichment analysis is carried out as a hypergeometric test, and the FDR level is set to 0.05 (see Supplementary Table S2).

2.8 Comparisons with other algorithms

The network clustering algorithms are evaluated by judging how well the predicted clusters are mapped to the MIPS protein complex, KEGG pathways and GO functional categories. Song et al. (2009) provided a basic framework to compare network clustering algorithms. The evaluation measures, including Jaccard measure, PR measure and semantic density measure, are described briefly here.

Let G = {G₁, G₂,…, G_n} be a set of annotated functional gene groups, and let C = {C₁, C₂,…, C_m} be a set of predicted clusters. N is the total number of genes in the network. The Jaccard similarity of two sets is defined in Equation 14. The Jaccard measure between the predicted clusters and the functional gene sets is defined in Equation 15, which is a weighted average over the size of each cluster.

(14)

(15)

The precision-recall (PR) measure of two sets is defined in Equation 16. The PR measure between C and G is similarly defined (Equation 17).

(16)

(17)

Besides the Jaccard and PR measures, semantic density is defined to consider the hierarchical nature of GO terms (see Supplementary Method 2).

3 RESULTS

3.1 Predicting modules in the genetic interaction network

The extent of functional correspondence of any two genes in a genetic interaction network can be characterized on two levels. First, the genetic interactions of one gene against the library of genes in the genome form a genetic interaction profile, and the similarity among genetic interaction profiles is indicative of the partnership of the pair of genes. Their similarity is measured as the Pearson correlation coefficient (PCC) of the genetic interaction profiles (Collins et al., 2006). Second, the discrepancy between the observed phenotype of the double mutation and the expected phenotype with regard to each single mutant is reflected from the EMAP measures. PCCs have been used as the similarity measure in cluster analysis (Schuldiner et al., 2005), which clusters together genes participating in common biological processes. Such clustering strategies tend to find groups of genes that act in a consistent manner across the entire library. This may be true for protein complexes, but it is not always applicable to genes in common pathways, especially if they participate in multiple pathways and functions. Moreover, such strategies often neglect gene pairs with strong S scores, but poor PCCs, which could also be informative, as discussed above.

Borrowing ideas from the analysis of PPI networks (Sharan et al., 2005a, b), we propose to identify modules from the genetic interaction network. ‘Module’ refers to a set of genes that are enriched for pair-wise interactions. In a Bayesian probabilistic framework, modules can be predicted from the probabilistic genetic interaction network (see Section 2). We have designed a new approach, rather than directly applying established cluster algorithms in PPI networks, because genetic interaction networks differ from PPI networks in their topological structures, which have a major impact on the performance of the algorithms (Song et al., 2009). In a genetic interaction network, the average network clustering coefficient is much larger (see Supplementary Table S5), regardless of the choice of cutoff.

Applying the algorithm in the ESP EMAP dataset, we predicted 27 modules (see Supplementary Text 1). Two of the modules are enriched in a MIPS protein complex, four are enriched in a KEGG pathway and 14 are enriched in GO terms (see Supplementary Table S2). The experimental results of our method is described, evaluated and compared with existing methods in Section 3.2.

3.2 Module prediction in the ESP EMAP dataset, compared with HC and MCL

To determine whether our approach has any advantage over existing methods, a detailed comparison was conducted. We considered two algorithms for comparison. The first one is HC analysis (Supplementary Method 3), which is widely used in analyzing genetic interaction networks to infer protein complexes and cellular pathways (Collins et al., 2006; 2007b; Costanzo et al., 2010; Schuldiner et al., 2005). The second one is MCL (Supplementary Method 4), which is based on simulating random walks in a network (van Dongen et al., 2000). A recent study compared several network clustering algorithms, and the authors concluded that MCL outperforms others in PPI networks (Brohee et al., 2006).

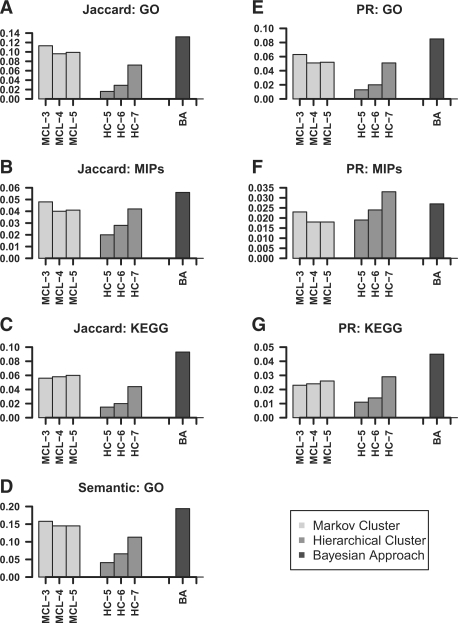
The framework provided by Song et al. (2009) is exploited for the comparison. The results demonstrated that our method outperforms both HC and MCL in Jaccard measure, PR measure and semantic density measure (Fig. 1). Moreover, our method significantly outperforms HC and MCL in all three measures with respect to GO terms and KEGG pathways (Fig. 1A, C, D, E, G). In PR measure, HC is slightly better than our method when mapped to MIPS protein complexes.

Fig. 1.

Comparison of the Bayesian approach (BA) with other methods (MCL and HC). Different inflation parameters (3, 4, 5) were used for MCL. Different cutoffs were used for HC (0.5, 0.6, 0.7). Comparison of Jaccard measure with respect to GO terms (A), KEGG pathways (B), MIPS protein complex (C); comparison of semantic density of GO terms (D); comparison of PR measure with respect to GO terms (E), KEGG pathway (F) and MIPS protein complex (G). In all three measures, the larger value corresponds to better performance.

In addition, we examined the overlap between the modules predicted by our method and the clusters predicted by HC. There are 13 modules that significantly overlap with the cluster method, while the others represent distinct discoveries by our method (see Supplementary Table S4).

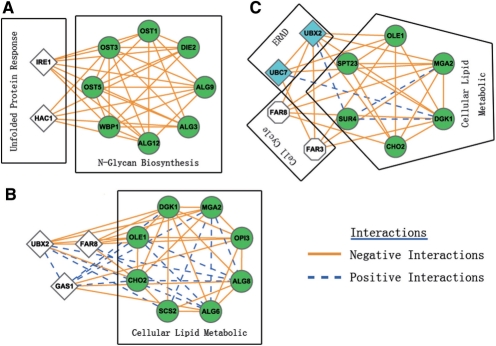
For cases in which our modules overlap with the clusters identified with HC (Schuldiner et al., 2005), our modules tend to contain additional information about pathway cross talk. For example, 8 genes in module 22 participate in the N-Glycan biosynthesis pathway in KEGG (Fig. 2A). The same eight genes are also clustered together by HC (Supplementary Method 3). However, our module includes two additional genes: Ire1 and Hac1. It is well known that these two genes work together to transcriptionally upregulate the genes involved in the unfolded protein response (UPR) pathway in response to misfolded proteins in the ER (Jonikas et al., 2009). When glycosylation is inhibited, the most commonly observed effect is the generation of misfolded proteins (Helenius and Aebi, 2001), suggesting cross talk between the N-Glycan biosynthesis pathway and the UPR pathway. Our method captured the extensive interaction and cross talk between the two pathways.

Fig. 2.

Examples of the modules identified in the ESP EMAP dataset. (A) The module is enriched in the N-Glycan biosynthesis pathway in KEGG; (B) the module is enriched in the cellular lipid metabolic process in GO; (C) the module possibly carries cross talk between pathways. The figure was produced using Cytoscape (Shannon et al., 2003).

There are a number of modules that are identified by our method, but missed by HC. For example, in module 15, 8 out of 11 genes are annotated as ‘cellular lipid metabolic process’ (Fig. 2B). The genetic interaction profiles among them are poorly correlated, so these genes are distributed into distinct subgroups by HC. Nevertheless, the dense interactions among these genes are revealed by our method.

More than 50% of the modules we predicted are supported by functional evidence from diverse sources. However, the other modules are also biologically informative. Other than working in the same biological pathways, genes in a module can often mediate cross talk between different pathways. For instance, in module 25 (Fig. 2C), MGA2 and SPT23 are transcriptional regulators of OLE1, which is a delta (9) fatty acid desaturase, which is required for monounsaturated fatty acid synthesis. OLE1 is short lived and regulated by ER-associated degradation (ERAD) (Braun et al., 2002). SEL1 and UBC7 in module 25 are involved in the ER-associated protein degradation pathway, and the dense interactions in the module can be explained by the cross talk between the OLE and ERAD pathways. This kind of information from EMAP data is hard to capture with cluster analysis.

3.3 Mixture modeling

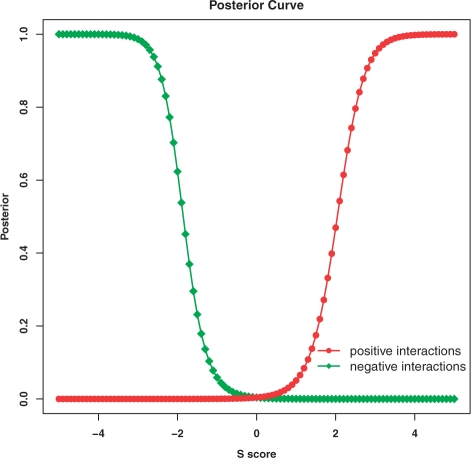
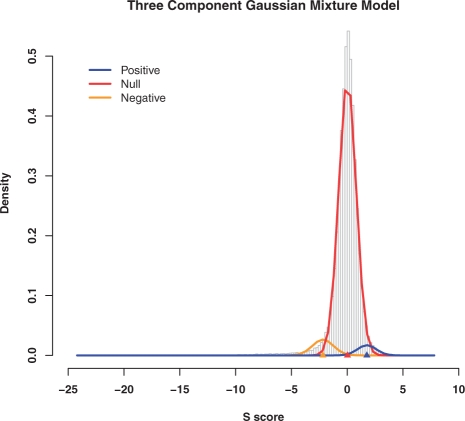
We applied a three-component Gaussian mixture model (see Section 2) to fit the distribution of S scores. For each pair of genes in the EMAP dataset, the posterior probability that the S score corresponds to a positive and negative genetic interaction is derived from the model. The S score versus posterior probability curve in the phosphorylation EMAP dataset is shown in Figure 3, and the fitting of mixture model on the same dataset is shown in Figure 4.

Fig. 3.

The mixture model was trained on the phosphorylation EMAP dataset. The positive and negative posterior probability curves are shown.

Fig. 4.

Fitting of the mixture model on the phosphorylation EMAP dataset. The gray bars are the histogram of the original S scores. The yellow, red and blue curves are the density of the negative, null and positive interactions, respectively. The triangles indicate the mean value of the respective normal distribution.

Our mixture modeling is a soft threshold technique. Alternatively, one can arbitrarily choose a cutoff and output a discrete genetic interaction network. However, there are two limitations with hard threshold. First, when a threshold such as 2.0 is chosen, scores from 0 to 2.0 are not regarded as significantly different. Second, the threshold is arbitrarily chosen. Therefore, we assign a posterior probability to each gene pair and output a probabilistic genetic interaction network. The probability represents the discrepancy between the observed double mutant phenotype and the expected phenotype. Such a probabilistic network carries the quantitative information of EMAP into further inference so that a moderately scored interaction can be detected, if supported by other evidence.

3.4 Prediction of positive triplet motifs

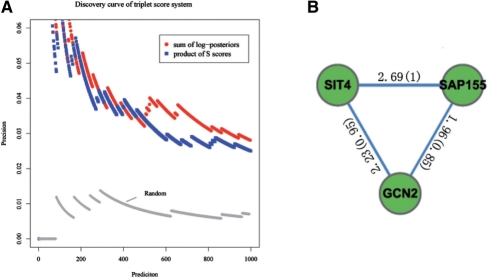
To illustrate the advantage of the soft threshold property of the mixture model, we predicted positive triplets with original S scores (Fiedler et al., 2009) and their posterior probabilities, respectively (see Section 2). We compared the precision of our method (Method 1) with the method in Fiedler et al. (2009) (Method 2) (Fig. 5A). The high-scoring triplets at different cutoffs for both methods are shown in the figure. Their performance is comparable, no matter whether an extremely stringent or a very loose cutoff is applied. When a moderate cutoff is used, our method catches more verified interactions, demonstrating its ability to detect subtle interactions. Actually, a stringent cutoff will result in a high false negative rate, which is not desirable in large-scale studies. In summary, our method outperforms the method using direct S scores.

Fig. 5.

Comparison of two methods in predicting triplet motifs. (A) Precision curve of both methods. Method 1 (red): a triplet is scored as the sum of log posteriors. Method 2 (blue): a triplet is scored as the product of S scores. Random (gray): the triples are randomly sampled in the genetic interaction network. The x-axis is the number of interactions in the positive triplets. The y-axis is the number of true positive interactions divided by the corresponding values of the x-axis. (B) An example triplet predicted by our method (Method 1). The values around the edges are the S scores of the corresponding interaction, and the values in the parentheses are the corresponding probabilistic scores.

Method 2 usually predicts triplets with extremely large S scores and misses those with three moderately large S scores. Our method, on the other hand, is not affected by extreme S scores, which could originate from either true interaction or noise. For example, the triplet (SAP155, GCN2, SIT4) is ranked among top 500 by our method (Fig. 5B). SIT4 is a phosphatase that functions in G₁/S transition in the mitotic cell cycle (Sutton et al., 1991). SAP155 forms a complex with SIT4 protein, and is required for the function of SIT4 (Luke et al., 1996). Plus, GCN2 is the substrate of SIT4 (Cherkasova et al., 2003). These evidences suggest SAP155, GCN2, SIT4 is a biologically significant triplet, and the pair-wise interactions in the triplet have large S scores (Fig. 5B). The rank of this triplet by Method 2 is below 1000, which is much lower than the rank by our method.

4 DISCUSSION

Large-scale genetic interaction networks can be measured in model organisms like Escherichia coli, S.cerevisiae and S.pombe (Dixon et al., 2009; Tong et al., 2004). As more and more experimental data are generated, it becomes very challenging to interpret the biologically significant results in a way that can be experimentally verified. In this article, we proposed a Bayesian approach to identify modules in a probabilistic genetic interaction network obtained by mixture modeling of EMAP data. Our evaluation and comparison with other state-of-the-art algorithms (HC and MCL) demonstrated that our method could identify modules with high efficiency. Also, the posterior probability derived from mixture modeling, which is based on a soft threshold, proved to be a better quantitative measure than the S score in predicting triplet motifs with biological significance.

We also found that high PCC and large posterior probability are both associated with functional similarity and that they can complement each other in biological modules. Higher efficiency can be expected if these two measures are combined to identify modules in the genetic interaction network. Therefore, in the future, we will focus on developing network clustering algorithms that combine PCC and posterior probability.