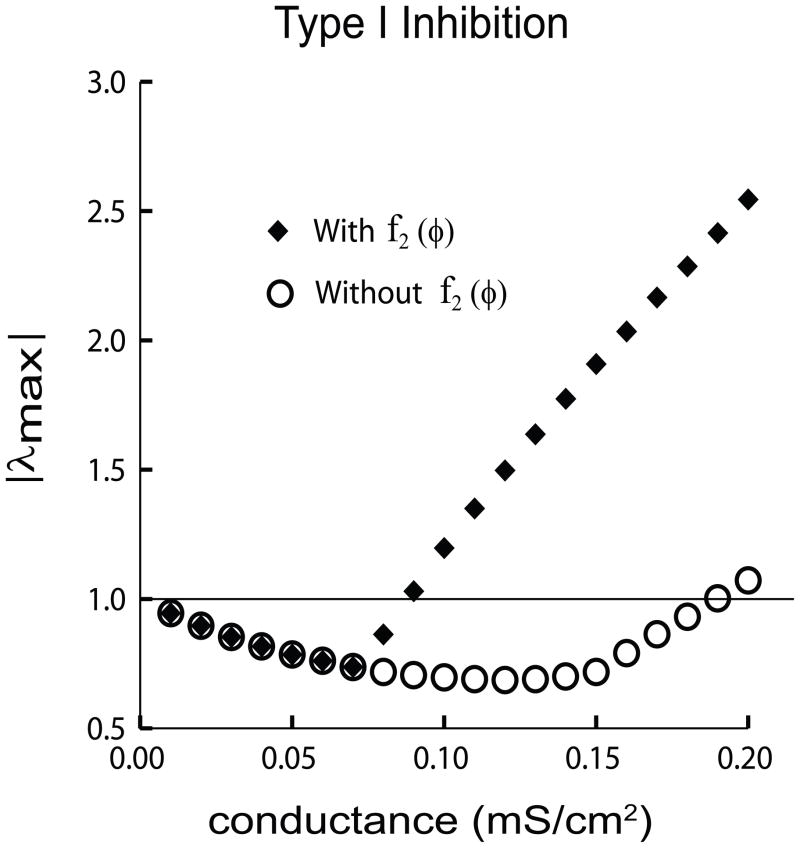
Fig. 5.
Importance of Second Order Resetting. Comparison of |λmax| for the case in which f2(φ) is neglected (without f2(φ), open circles) and the case in which it is considered (with f2(φ), filled diamonds) plotted against the synaptic conductance strength. For both cases, |λmax| is less than one up to .07 mS/cm2, predicting stability for the two cluster solution. In this range, the eigenvalue with the largest absolute value is |λ1|, which does not include a contribution from f2(φ). Beyond .07 mS/cm2 when f2(φ) is considered (filled diamonds), the eigenvalue with the the largest absolute value is λ2, which correctly predicts that the cluster mode loses stability for conductances greater than .08 mS/cm2. This diverges from the case where f2(φ) is ignored (open circles); neglecting f2(φ) incorrectly predicts stability up to .18 mS/cm2 (circles).