FIGURE 6.
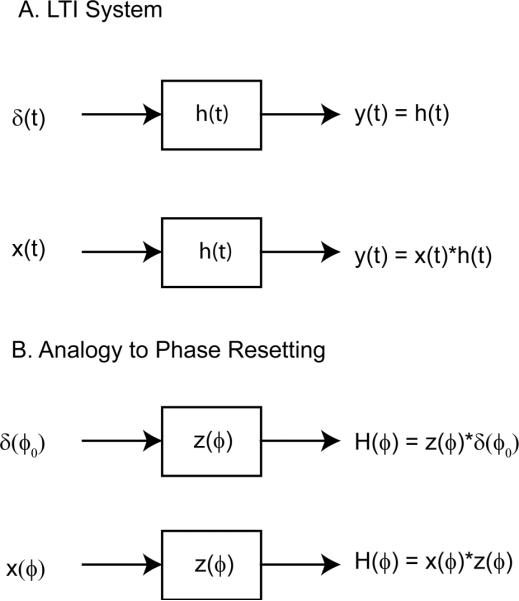
Analogy between linear systems theory and phase resetting theory under the assumption of weak coupling. (A) The output y(t) of a linear time invariant system (LTI) produced by an input waveform x(t) is the convolution (represented as *) between x(t) and the response h(t) of the LTI to a unit impulse, δ (t). (B) The phase response curve, H(ϕ) generated using an arbitrary input waveform x(ϕ) is obtained by convolving x(ϕ) with the infinitesimal phase response curve z(ϕ). The phase resetting is assumed to be time (phase) dependent but instantaneous such that a convolution can still be performed despite the absence of a time invariant shifting property.
