Macromolecular dynamics in red blood cells investigated using neutron spectroscopy

Abstract

We present neutron scattering measurements on the dynamics of haemoglobin (Hb) in human red blood cells (RBCs) in vivo. Global and internal Hb dynamics were measured in the ps to ns time and Å length scales using quasi-elastic neutron backscattering spectroscopy. We observed the cross over from global Hb short-time to long-time self-diffusion. Both short- and long-time diffusion coefficients agree quantitatively with predicted values from the hydrodynamic theory of non-charged hard-sphere suspensions when a bound water fraction of around 0.23 gram H₂O per gram Hb is taken into account. The higher amount of water in the cells facilitates internal protein fluctuations in the ps time scale when compared with fully hydrated Hb powder. Slower internal dynamics of Hb in RBCs in the ns time range were found to be rather similar to results obtained with fully hydrated protein powders, solutions and Escherichia coli cells.

1. Introduction

Ongoing research is dedicated to obtaining a coherent picture of the interactions and dynamical properties of proteins in their physiological environment. Cells are highly complex objects which are composed of organelles, tens of thousands of different proteins, RNA and DNA, lipids, polysaccharides and many other chemical components. Red blood cells (RBCs) in this sense are exceptional. They are highly specialized and relatively simple in their composition with the main macromolecular component, haemoglobin (Hb), making up 92 per cent of the dry weight. The concentration of Hb in RBCs is c = 0.33 g ml⁻¹ with a corresponding volume fraction of ϕ = 0.25 [1]. The hydrodynamic radius of Hb is approximately 32 Å [2], and the average distance between Hb molecules is in the order of 1 nm [1]. RBCs are therefore particularly well-suited model systems to study the physical properties of concentrated protein solutions in vivo.

From a biological point of view the properties of human RBCs are interesting to study as well because they exhibit a variety of remarkable properties. RBCs have been shown to undergo a passage transition through narrow micropipettes at body temperature [3]. The single cells were aspirated with a micropipette (diameter of the pipette tip approx. 1.5 µm) and, at temperatures lower than body temperature, all cells blocked the pipette. Above body temperature all aspirated RBCs passed through the narrow micropipette tip easily without any apparent resistance. The passage temperature was 36.3 ± 0.3°C, which is remarkably close to human body temperature [3]. It was found that the passage behaviour is caused by a reduction in the viscosity of the concentrated Hb solution in the RBCs [3]. The loss of viscosity and the passage transition in the micropipette experiments were found to be connected to perturbations and partial unfolding of the structure of Hb at body temperature [4]. Further studies revealed that the structural perturbations of Hb at body temperature lead to Hb aggregation above approximately 37°C [2], and concomitantly RBCs release cytosolic cell water to the outside blood plasma as observed in colloid osmotic pressure measurements [5]. A direct correlation between the structural perturbation temperature of Hb and the body temperature of a large variety of different species was reported, which further supported the biological relevance of the effect [2,6]. It was speculated that the partial loss of Hb structure causes an increase in surface hydrophobicity, which might result in stronger protein–protein interactions and thus lead to protein aggregation above body temperature [2,7,8].

Krueger and co-authors [1,9] studied the interactions of Hb in RBCs and concentrated solution and demonstrated that a hard-sphere potential plus screened electrostatics can approximately describe the protein–protein interaction potential. The same results were also obtained later for concentrated myoglobin solutions [10]. It might be of interest to note that studies on concentrated solutions of crystallins and lysozyme demonstrated that a delicate balance between hard-sphere and weak attractive interactions are crucial for the stability of these concentrated protein solutions [11–13]. In further experiments, Doster & Longeville [14] examined the diffusion of Hb in RBCs using neutron spin-echo spectroscopy. The authors had the idea to interpret the diffusion of Hb in RBCs using the theory of colloidal diffusion at high concentration. The neutron spin-echo technique is sensitive to molecular motions occurring in the ns and nm time and length scales. Doster & Longeville [14] compared the measured short-time and long-time self-diffusion coefficient of Hb with theoretical calculations of non-charged hard-sphere suspensions with direct and hydrodynamic interactions. It was necessary to include the hydration shell as a hydrodynamic coat to account for the discrepancy with colloidal theory. Furthermore, it was deduced that hydrodynamic and not direct interactions dominate Hb diffusion at high concentration.

Without hydration water, proteins would neither fold correctly [15–17] nor acquire the conformational flexibility which is considered relevant for biological activity [18]. Motions in proteins occur over a very large range of time scales from fast reorientations of amino acid side chains in the ps range, to slower motions of the protein backbone in the ns time scale and to very slow processes of protein subunits and folding processes in the µs and ms range [19]. Fast fluctuations in the ps and ns time scales are considered to act as lubricants and to enable much slower physiologically important motions [20]. Hydration-dependent internal protein dynamics has been studied with incoherent neutron scattering in several model systems mainly as hydrated powders, including myoglobin [21,22], lysozyme [23–25] and α-amylase [26–28]. In incoherent neutron scattering experiments, the single particle motions of hydrogen (H) atoms are detected. H atoms are indicators of average protein dynamics as they constitute approximately 50 per cent of the atoms and are uniformly distributed in the macromolecules [29]. Hydration water not only enables protein dynamics but participates actively in protein function. Around 60 additional water molecules are bound in the hydration layer of the oxygenated form of Hb as compared with the deoxygenated state of Hb [30]. The additional water molecules were found to be thermodynamically important for regulation of Hb activity. The study carried out by Colombo and co-workers [31] was done in an aqueous solution at a Hb concentration of 64 mg ml⁻¹. Further studies revealed that binding of the extra water molecules is the rate-limiting step of Hb activity. Therefore, an important question is whether protein dynamics is adapted to the specific hydration level in cells.

In this paper, we present a study of Hb dynamics in RBCs in the ps to ns time- and Å length scales using high-resolution quasi-elastic neutron scattering (QENS). The aim of the study is to demonstrate how QENS allows the measurement and separation of internal protein dynamics and global macromolecular diffusion in whole cells. The QENS technique provides complementary information to fluorescent correlation spectroscopy [32,33] or neutron spin-echo spectroscopy [14,34,35], which are sensitive to different time–space windows of protein fluctuations.

2. Material and methods

2.1. Sample preparation

Samples of human venous blood from healthy adults were drawn into tubes containing heparin to prevent blood coagulation. RBC samples were prepared as described in Stadler et al. [7]. During the sample preparation, the RBCs were gassed with CO to increase the stability of Hb and the glycocalyx matrix was removed. The cells were washed several times with D₂O 4-(2-hydroxyethyl)-1-piperazineethanesulphonic acid (HEPES) buffer (137 mM NaCl, 4 mM KCl, 1.8 mM CaCl₂, 0.8 mM Na₂HPO₄, 0.2 mM NaH₂PO₄, 0.7 mM MgSO₄, 8.4 mM HEPES and 4 mM NaOH) at pD = 7.4 and 290 mOsm to reduce the neutron scattering contribution of the buffer. The washing steps were repeated until the level of H₂O was estimated to be below 0.1 vol.%. The shape of the cells was checked with optical microscopy after the washing steps. The cell pellet was sealed in a flat aluminium sample holder of 0.2 mm thickness for the neutron scattering experiment. It was checked by weighing that there had been no loss of sample material during the experiment.

2.2. Dynamic light scattering experiments

Samples for the dynamic light scattering experiments were prepared from a drop of blood taken from the finger tip. The RBCs were washed with H₂O HEPES buffer and lysed with distilled water. The sample for dynamic light scattering experiments was not gassed with CO. Before the dynamic light scattering experiments, the dilute Hb solution in H₂O buffer (0.1 M KCl, 61.3 mM K₂HPO₄, 5.33 mM KH₂PO₄, pH 7.4, 290–300 mOsm) was centrifuged at 20 000 relative centrifugal force and filtered using 0.25 µm nitrocellulose filters. UV/VIS absorption spectroscopy was used to determine the concentration of the Hb solution. The Hb was found to be in the oxy-state as evidenced by the characteristic bands in the absorption spectrum, and the protein concentration was 0.4 mg ml⁻¹. The protein concentration was determined using extinction coefficients of 13.8 mM⁻¹ × cm⁻¹ at 541 nm and 128 mM⁻¹ × cm⁻¹ at 405 nm for oxy-Hb; the molar concentration is per haem group [36]. Dynamic light scattering of dilute human Hb solution was measured on a Wyatt DAWN-EOS instrument (Wyatt Technology, Santa Barbara, CA) and corrected for temperature-dependent D₂O viscosity using literature values [37]. The diffusion coefficients were calculated using the Astra 5 software package from the manufacturer. Around 5 ml of sample was measured per experiment.

2.3. Neutron scattering experiments

Neutron scattering was measured on the high-resolution neutron backscattering spectrometers IN10 and IN16 at the ILL (http://www.ill.eu/instruments-support/instruments-groups/yellowbook/) and IRIS at the ISIS spallation source (http://www.isis.stfc.ac.uk/instruments/iris/). To minimize multiple scattering, RBC samples with high transmissions were used (0.95 on IN16 and IRIS and 0.9 on IN10). The instruments IRIS, IN10 and IN16 are characterized by energy resolutions ΔE of 17, 1 and 0.9 µeV (FWHM), respectively, which correspond to slowest observable motions in the order of of approximately 40 ps and 1 ns, respectively. Neutron scattering was measured in the range of 0.49 ≤ q ≤ 1.6 Å⁻¹ on IN16, 0.5 ≤ q ≤ 1.45 Å⁻¹ on IN10 and 0.48 ≤ q ≤ 1.6 Å⁻¹ on IRIS, where q is the modulus of the scattering vector. The instrumental energy resolution was determined with a vanadium measurement. The scattering contribution of the empty aluminium sample holder was subtracted from the measured data. Neutron detectors were grouped on IN16 and IRIS to obtain better statistics. Incoherent scattering of D₂O solvent contributes partially to the measured intensities: free and interfacial water dynamics are out of the Å-ns space and time window of IN10 and IN16 and contribute only as a flat background to the measured spectra [38]. Experimental data are dominated by Hb motions on the IRIS spectrometer, and the incoherent contribution of D₂O on IRIS is estimated to be smaller than 4 per cent at q < 1.3 Å⁻¹ [7]. Gaspar et al. [39] evaluated the coherent and incoherent scattering contributions of concentrated protein solutions in D₂O solvent. In a completely dry myoglobin powder the authors found an incoherent scattering fraction of approximately 90 per cent and a coherent scattering fraction of approximately 10 per cent between 0.5 and 1.5 Å⁻¹. For a concentrated myoglobin solution of 360 mg ml⁻¹, the authors reported an incoherent scattering fraction of around 80 per cent and a coherent scattering fraction of around 20 per cent between 0.5 and 1.5 Å⁻¹. The coherent scattering fraction of D₂O in the 360 mg ml⁻¹ solution therefore has to be approximately 10 per cent in that scattering vector range. In RBCs the protein concentration is 330 mg ml⁻¹ and the values should be comparable.

3. QENS data analysis

The scattering function of internal protein dynamics S_I(q,ω) can be written in a simplified form as an elastic term and a single Lorentzian that represents internal protein diffusive motions [29]

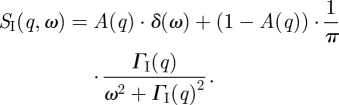3.1

The prefactor A(q) is called the elastic incoherent structure factor (EISF), q is the modulus of the scattering vector and Γ_I(Q) are the half-widths at half-maximum (HWHM) of the Lorentzian. The q-dependence of the EISF contains information about the geometry of localized motions, and the scattering vector dependence of Γ_I(q) provides information about the diffusion coefficients and residences times of diffusive motions.

Global macromolecular diffusion consists of translational and rotational diffusions of the protein. The scattering function of global protein diffusion S_G(q,ω) is the convolution of the scattering functions of translational and rotational diffusions assuming that rotational and translational diffusions are uncorrelated. It was shown theoretically by Perez et al. [40] that rotational diffusion of a protein leads to an additional broadening of the measured HWHM. The scattering function S_G(q,ω) could be approximated by a single Lorentzian with the half-widths Γ_G(q),

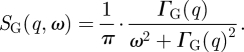3.2

The line-widths and the apparent diffusion coefficient D_app of the protein are related by Γ_G(q) = D_app · q² [40]. The apparent diffusion coefficient D_app was compared with D₀, which is the translational diffusion coefficient of the protein at infinite dilution. The identical value of D_app/D₀ = 1.27 was obtained for myoglobin and haemoglobin [7,40]. The calculation of the contributions of rotational and translational diffusions to the measured spectra is described in appendix A.

Furthermore, it is assumed that internal protein dynamics and global protein diffusion are uncorrelated in concentrated protein solutions. The scattering function S(q,ω) then is the convolution between S_I(q,ω) and S_G(q,ω), S(q,ω) = S_I(q,ω) ⊗ S_G(q,ω) [41]. The scattering function reads as

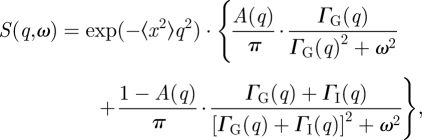3.3

where the exponential represents a Debye–Waller factor for fast molecular vibrations. S(q,ω) plus linear background was convoluted with the instrumental resolution function and fitted to the measured QENS spectra in the energy range of −14 ≤ E ≤ +14 µeV for IN16, −12.4 ≤ E ≤ +12.4 µeV for IN10 and −0.5 ≤ E ≤ +0.5 meV for IRIS using the Dave software package [42].

Gaspar et al. [43] demonstrated that the half-widths of internal motions Γ_I(q) are a weaker parameter than the EISF. The authors could fit measured QENS spectra equally well with constant or freely varying line-widths as a function of the scattering vector. As a test we fixed the line-widths of internal motions to the q-independent average value of Γ_I(q) = 0.2 meV. The obtained line-widths Γ_G(q) of global Hb diffusion were then found to increase linearly with q² as expected but did not intercept zero at q²→0. A non-zero intercept at q²→0 of global protein diffusion is difficult to interpret with global Hb diffusion. On the other hand, when the line-widths Γ_I(q) were allowed to vary freely, we obtained line-widths Γ_G(q) that pass through zero as expected for global protein diffusion.

4. Results and discussion

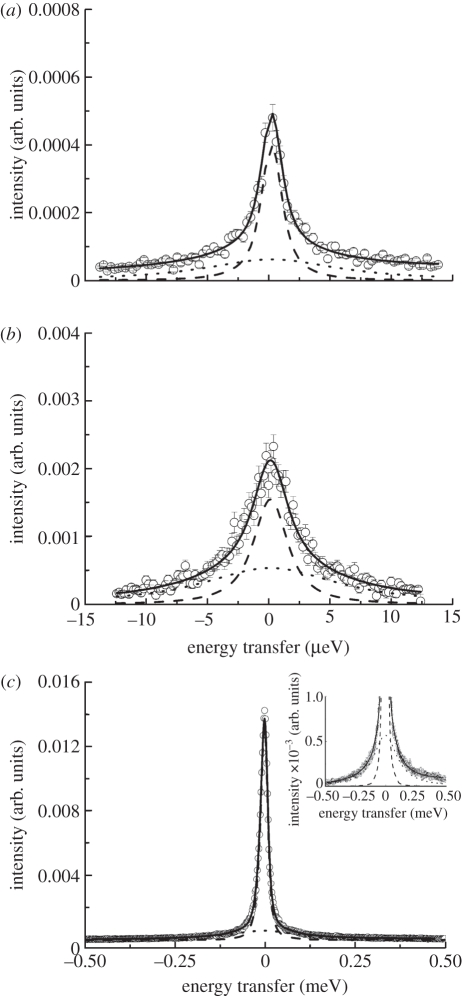
In the following we present and discuss the results of our experiments. Typical QENS data measured on the neutron spectrometers IN16, IN10 and IRIS are shown in figure 1. The measured spectra were well described with a narrow and a broad Lorentzian for global macromolecular diffusion and internal Hb dynamics, respectively. First, we discuss the results about global Hb diffusion. Our interpretation follows the ideas of Doster & Longeville [14].

Figure 1.

Experimental QENS data of Hb in RBCs measured on (a) IN16 at 11.9°C and q = 1.3 Å⁻¹, (b) IN10 at 19.1°C and q = 1.45 Å⁻¹ and (c) IRIS at 16.9°C and q = 1.37 Å⁻¹. The solid black line is the total fit, and the dashed and the dotted lines represent, respectively, the narrow and broad Lorentzians used for data analysis. The inset in (c) on the right-hand side shows a magnification of the spectrum measured on IRIS to illustrate the quality of the fit. The instruments IRIS, IN10 and IN16 are characterized by energy resolutions ΔE of 17, 1 and 0.9 µeV (FWHM), respectively.

4.1. Global macromolecular diffusion

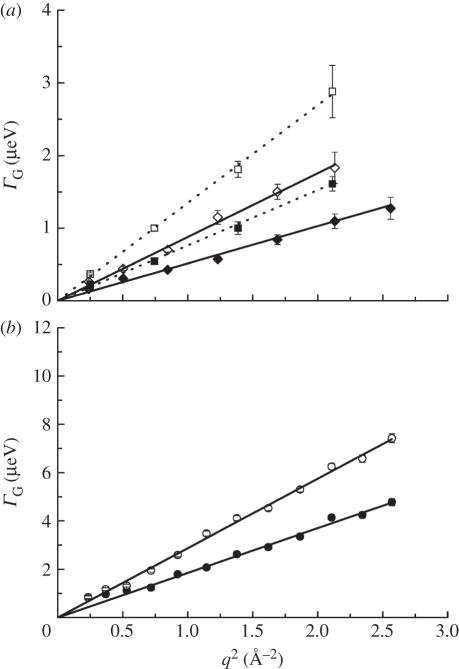
The measured HWHM for global Hb diffusion are presented in figure 2. Apparent diffusion coefficients D_app were determined according to Γ_G(q) = D_app · q² in the range of 0.24 ≤ q² ≤ 2.56 Å⁻² for IN10 and IN16 data, and in the range of 0.72 ≤ q² ≤ 2.57 Å⁻² for IRIS data. The line-widths Γ_G(q) of global Hb diffusion increase linearly with q² up to around 2.6 Å⁻². This behaviour is a clear sign of continuous global diffusion of Hb. The D_app contains a component of both translational and rotational diffusions of Hb. It was shown previously [7,40] that rotational diffusion of Hb leads to an additional broadening of the spectra by a factor of 1.27. Therefore, the apparent diffusion coefficients D_app were divided by 1.27 to obtain the global translational diffusion coefficient D of Hb. The essential steps in the calculation of the contributions of rotational and translational diffusions to the experimental spectra are outlined in appendix A. All obtained values of D are compared in figure 3. The line-widths obtained from the measurements with IN16 and IN10 intercept zero (figure 2a), which indicates that on time scales of approximately 1 ns global Hb diffusion does not sense confinement of neighbouring proteins. The Γ_G(q) measured on IRIS appear to converge towards a plateau at small q² and low temperature (figure 2b). The feature indicates a cage effect of the neighbouring molecules on Hb diffusion in the ps time scale and has been observed before [7]. Multiple scattering might lead to a deviation from linear behaviour at small q². However, as the transmission of the sample was 0.95 multiple scattering should be completely negligible. An alternative explanation could be that small uncertainties of the resolution function might result in a plateau at small q², as the HWHM are only approximately 10 per cent of the energy resolution of IRIS. An observation time-dependent diffusion coefficient is obtained. Unruh et al. [44] observed a similar phenomenon. The authors studied the motions in liquid medium-chain n-alkanes using QENS with observation times from 1.1 to 900 ps and molecular dynamics simulations. The study revealed a time-dependent diffusion coefficient, and there was no need to use the obtained half-widths at low-resolution for the analysis of the high-resolution data. To check the validity of our interpretations, we have also performed a complementary analysis in time–space (see electronic supplementary material). The obtained diffusion coefficients in time–space and in energy–space are identical within the error bars. If the diffusion coefficient measured with IRIS is visible with IN16/IN10, we would obtain a mixture in time–space of the IRIS and the IN16/IN10 energy–space results. This is not the case and our check therefore demonstrates the validity of our analysis.

Figure 2.

Half-widths at half-maximum of the Lorentzians of global Hb diffusion in RBCs measured with QENS on (a) IN16 (diamonds), IN10 (squares) (open square, 36.5°C, open diamond, 26.9°C; filled square, 19.1°C; filled diamond, 11.9°C) and (b) IRIS (open circle, 36.9°C; filled circle, 16.9°C). The straight lines are linear fits to the data. In (a) the solid lines are fits to IN16 and the dotted lines are fits to IN10 data. The linear increase of the line-widths with q² is a clear sign of continuous global Hb diffusion. The diffusion coefficients of Hb were determined from the slope of the linear fits. IN10 and IN16 are sensitive to motions in the time scale of approximately ns, whereas IRIS detects motions in the time scale of approximately 40 ps.

Figure 3.

Diffusion coefficient D of Hb in RBCs as a function of temperature. The diffusion coefficients were measured with QENS on IRIS (circles), on IN16 (diamonds), on IN10 (squares) and with neutron spin-echo spectroscopy on IN15 (triangle) [14]. D₀ was measured with dynamic light scattering and scaled data points are given as small empty circles. The thin dotted and the thin dashed line show the theoretical values of short-time 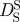and long-time self-diffusion 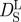of Hb at a volume fraction of ϕ = 0.25 with hydrodynamic interactions (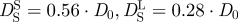) [47]. The thick dotted and the thick dashed line represent the theoretical values for short-time and long-time self-diffusion of Hb assuming that a hydration layer of 0.23 gram H₂O per gram protein is bound to the surface of Hb. Experimental data agree well with the theoretical considerations when the bound hydration water layer is taken into account (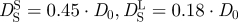) [47].

Studies on average macromolecular dynamics in Escherichia coli cells [45] and in concentrated myoglobin solutions [46] using high-resolution neutron backscattering spectroscopy reported that the measured line-widths of global macromolecular diffusion deviate from linear behaviour and tend towards saturation at large q². Jump-diffusion of the macromolecules was discussed as a possible explanation [45,46], as this mechanism would result in a saturation of the line-widths at large q². On the other hand, a distribution of diffusion coefficients could also be responsible for the deviation of the line-widths from linear behaviour [46]. Importantly, any kind of non-localized diffusion leads to line-widths that tend towards zero with Γ_G(q) = D_app · q² at small q²-values. Jasnin et al. [45] studied average macromolecular dynamics in E. coli using the IRIS spectrometer. Global macromolecular diffusion in E. coli was too slow and could not be resolved with IRIS. Prokaryotic cells, such as E. coli, are very complex objects which contain a vast amount of large macromolecular assemblies, such as ribosomes with a molecular mass of 2.5 MDa. Average macromolecular dynamics in E. coli are therefore difficult to attribute to a certain component. Hb is the main macromolecular component of RBCs with a rather small molecular mass of 65 kDa. It is reasonable to assume that global diffusion of Hb is significantly faster than that of large macromolecular complexes in E. coli, which would explain why Hb global diffusion in RBCs is visible on IRIS.

Tokuyama & Oppenheim [47] evaluated the short-time 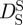and long-time 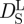self-diffusion coefficients of concentrated non-charged hard-sphere suspensions with hydrodynamic and direct interactions as a function of the volume fraction ϕ and of the diffusion coefficient at infinite dilution D₀. Short-time self-diffusion corresponds to particles that move in a static configuration of the neighbouring particles at times t < τ_D, with the structural relaxation time τ_D. The long-time limit of self-diffusion is reached at t > τ_D. The values of the short- and long-time self-diffusion coefficients are equal only in dilute solution. At higher concentrations short-time self-diffusion is always faster than long-time self-diffusion. We measured the diffusion coefficient D₀ of Hb at infinite dilution with dynamic light scattering. The theoretical values of 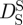and 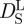of Hb at a volume fraction of ϕ = 0.25 (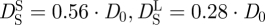) are given in figure 3 [47]. It is obvious that the measured diffusion coefficients are too small and do not agree with the theoretical values. Full hydration of myoglobin corresponds to a value of h ∼ 0.39 gram H₂O per gram Mb [18]. It is believed that the critical hydration, to allow the onset of anharmonic motions in myoglobin (Mb), is around h_Mb = 0.35 gram H₂O per gram Mb [22]. Hb has a larger radius of gyration than Mb (Hb: R_G ∼ 24 Å; Mb: R_G ∼ 16 Å) and a smaller surface to volume ratio (S/V) [10,48]. Approximating Hb and Mb as spherical particles, the critical hydration of Hb should be around h_Hb = (S/V)_Hb/(S/V)_Mb×h_Mb = 16 Å/24 Å×0.35 gram H₂O per gram Mb = 0.23 gram H₂O per gram Hb. It is known that the density of protein hydration water is approximately 10 per cent larger than the bulk solvent [49]. The partial specific volume ν of Hb plus hydration water is then ν = (0.75 + 0.23/1.1) ml g⁻¹ = 0.98 ml g⁻¹, which corresponds to an effective volume fraction of Hb plus hydration water of ϕ = c · ν = 0.32 with the concentration c = 0.33 g ml⁻¹ of Hb in RBCs [14,50]. The measured self-diffusion coefficients of Hb with IN16, IN10 and IRIS agree with high accuracy with the theoretical values of Hb plus the hydration shell (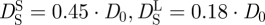; [47]). In a study on the short-time limit of Hb diffusion in RBCs we estimated that the structural relaxation time τ_D is of the order of several hundred ps [7]. Therefore, IRIS is sensitive to motions which are faster than τ_D and short-time self-diffusion is detected. The high-resolution instruments IN16 and IN10, and neutron spin-echo spectroscopy [14], measure motions which are longer than τ_D, and the long-time limit of Hb self-diffusion is observed. We showed previously that, although approximately 90 per cent of cell water in RBCs has properties similar to bulk water, a small fraction of approximately 10 per cent cellular water exhibits strongly reduced dynamics and was attributed to water molecules which are bound to the surface of Hb [51]. The ratio of water per Hb in RBCs is h ∼ 2.3 gram H₂O per gram Hb and an approximately 10 per cent fraction corresponds to a bound water fraction of approximately 0.23 gram H₂O per gram Hb, which is identical to the value reported in this article. Furthermore, Doster & Longeville [14] measured the diffusion of Hb in whole RBCs using spin-echo spectroscopy in the ns and nm time and length scales. The authors demonstrated that the presence of the hydration shell leads to a reduction in the diffusion coefficient of Hb. Garcia de la Torre [52] calculated hydrodynamic properties of proteins from atomic structures. It was demonstrated by comparing the calculated and experimental values that a hydration shell of h ∼ 0.27 gram H₂O per gram Hb is bound to the surface of Hb. Our result is reasonably close to that value.

4.2. Internal haemoglobin dynamics

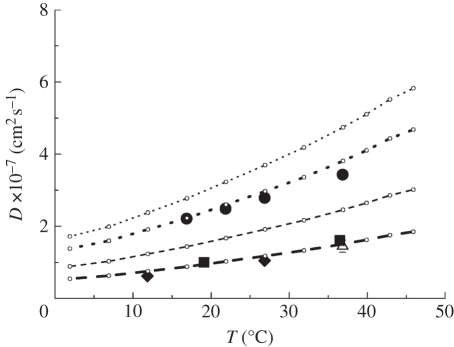
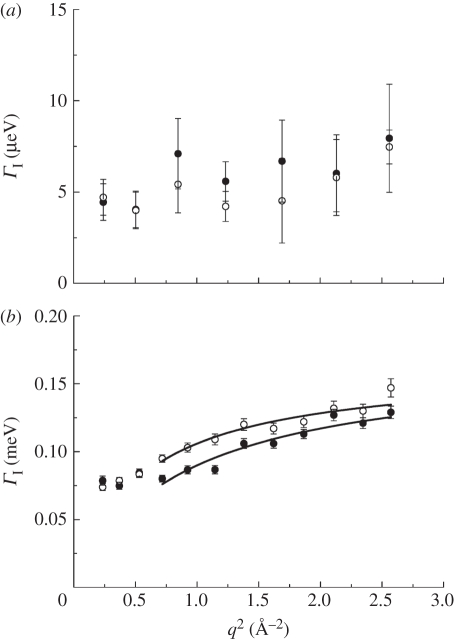
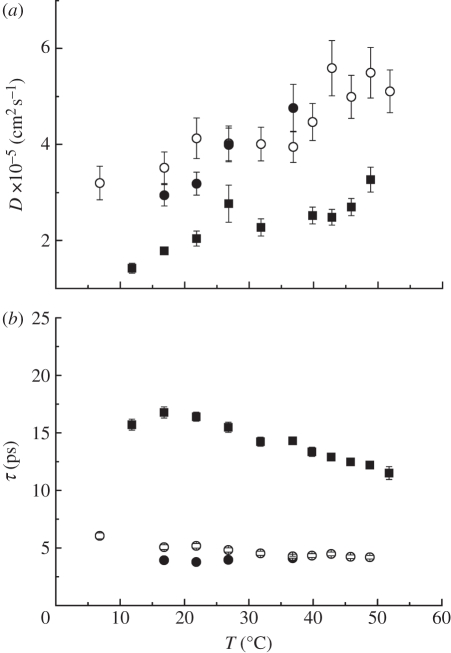
We now turn our attention to the results concerning internal protein dynamics. Detailed information about protein internal motions can be extracted from the scattering vector dependence of the quasi-elastic broadening and the EISF. The HWHM of internal protein dynamics measured on IN16 and on IRIS are given in figure 4a,b. The Γ_I(q) measured with IRIS show typical behaviour of localized jump-diffusion. The half-widths tend towards a constant value at small q², which indicates confining effects of local boundaries. Diffusive jumps with a finite jump-length lead to a plateau in the line-widths at large scattering vectors. In the q²-range of 0.72 and 2.57 Å⁻² the Γ_I(q,ω) measured on IRIS could be well described with a jump-diffusion model given by 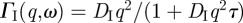[41]. The parameters of the jump-diffusion model are the residence time before a jump τ and the jump-diffusion coefficient D_I of protein internal motions. In figure 5, the jump-diffusion coefficients and the residence times of internal Hb dynamics in RBCs are compared with jump-diffusion coefficients and residence times of internal Hb dynamics as hydrated powder (h = 0.4 gram D₂O per gram Hb) and as concentrated solution (h = 1.1 gram D₂O per gram Hb). The corresponding hydration level in RBCs is h ∼ 2.5 gram D₂O per gram Hb. The results of the experiments with the hydrated Hb powder and concentrated Hb solution have been published before and are given here for comparison [8]. The Hb powder and solution were measured on neutron time-of-flight spectrometers with energy resolutions of 50 and 100 µeV, respectively. All data were analysed in the same way. The results demonstrate that an increase in the hydration level from one hydration shell in the Hb powder to around three hydration layers in the concentrated Hb solution increases the jump-diffusion coefficients and strongly reduces the residence times of internal protein dynamics in the ps time scale. A further increase in the hydration level to around six hydration layers per Hb in whole RBCs neither enhances the jump-diffusion coefficients nor reduces significantly the residence times as compared with the concentrated Hb sample. The rate of internal jump-diffusion in the ps time scale appears to be already fully developed in the concentrated Hb solution. The observed motions in the ps range could correspond to diffusive jumps of amino acid side chains and attached methyl groups [53].

Figure 4.

Half-widths at half-maximum of the Γ_I(q) of internal Hb dynamics as a function of q². Data in (a) were measured on IN16 (open circle, 26.9°C; filled circle, 11.9°C) and (b) on IRIS (open circle, 36.9°C; filled circle, 16.9°C). The scattering vector dependence of the line-widths contains information on the observed motions in Hb. Solid lines in (b) are fits with a jump-diffusion model in the q²-range from 0.72 to 2.57 Å⁻².

Figure 5.

(a) Diffusion coefficients of internal motions in Hb as a function of temperature. Results from fully hydrated Hb powder, solution and Hb in RBCs at different hydration levels are compared. (b) Residence times of internal jump-diffusion as a function of temperature of the different samples. Hb in RBCs was measured on IRIS at ISIS (energy resolution 17 µeV), concentrated Hb solution on TOFTOF at FRM-II (resolution 100 µeV) and hydrated Hb powder on FOCUS at PSI (resolution 50 µeV; filled circle, Hb in RBCs; open circle, Hb h = 1.1 gram D₂O per gram Hb; filled square, Hb h = 0.4 gram D₂O per gram Hb).

The half-widths of internal protein dynamics from the experiment on IN16 are independent of the scattering vector within the error bars, as shown in figure 4a, and have average values of 5.8 ± 1.4 µeV at 11.9°C and 6.2 ± 1.0 µeV at 26.9°C. The line-widths determined with IN10 are 5.5 µeV at 19.1°C and 4.2 µeV at 36.5°C. The Γ_I(q) on each individual spectrum of IN10 had large errors. The average value was used for all spectra at one temperature and held constant during fitting of IN10 data; the obtained values are rather imprecise and are given only for completeness. The line-widths obtained on IN16 and IN10 are in agreement with other studies which investigated protein dynamics in the ns time scale using high-resolution quasi-elastic neutron scattering. Fitter et al. [54] studied hydrated bacteriorhodopsin and obtained half-widths of 5.5 µeV; Orecchini et al. [55] investigated hydrated β-lactoglobulin powder and found half-widths of 16 µeV; Busch et al. [46] found line-widths of 10 µeV of myoglobin in concentrated solution; and Jasnin et al. [45] measured average dynamics in whole E. coli and obtained line-widths of approximately 7 µeV. If we exclude the lactoglobulin case, the values of the measured line-widths are rather similar, although the hydration levels in the investigated systems are different. We recall that correlation times τ and line-widths Γ are inversely related by τ_cor = 1/Γ. This seems to indicate that correlation times of motions in globular and membrane proteins in the ns time scale are rather similar in hydrated protein powders, solutions and in whole cells. As the observed line-widths on IN16 and IN10 are independent of the scattering vector, a different class of motions is observed using the high-resolution instruments. Rotational motions lead to line-widths which are independent of the scattering vector [41], and the observed dynamics might be attributed to slow rotations of side chains or relaxations of the protein backbone.

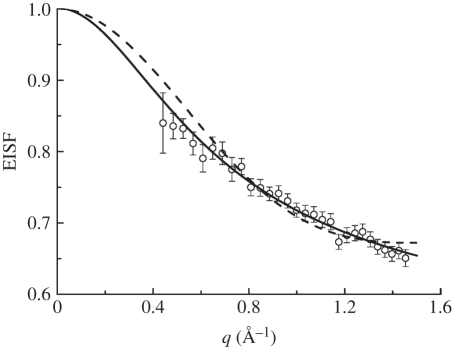
Information about the geometry of motions can be extracted from the measured EISF. Only four and six data points are available on IN10 and IN16, respectively. This is too few and does not allow an accurate analysis. Therefore, we limit our discussion to the results of the experiment using the IRIS spectrometer. The EISF obtained with IRIS at 26.9°C is shown in figure 6. The EISF was interpreted with the model of Volino & Dianoux [56] for diffusion in a sphere. The diffusion in a sphere model can be written as 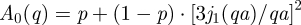, where j₁(qa) is the first-order spherical Bessel function of the first kind, a is the sphere radius and A₀(q) is the EISF. The hydrogen atoms which appear immobile and mobile within the instrumental energy resolution are represented by the fractions p and (1 − p), respectively. The obtained sphere radius a increases from 2.8 ± 0.1 Å at 16.9°C to 3.3 ± 0.1 Å at 36.9°C. The immobile fraction p has an average value of 0.67. These values reasonably agree with the results on macromolecular dynamics in E. coli, which found a = 3.1 Å and p = 0.61 at 6.9°C, and a = 3.4 Å and p = 0.56 at 26.9°C [45].

Figure 6.

Elastic incoherent structure factor of Hb in RBCs measured on IRIS at a temperature of 26.9°C. The dashed line is a fit with the model for diffusion in a sphere. The solid line is a fit with the model for diffusion in a sphere with a Gaussian distribution of sphere radii.

To take into account the heterogeneity of internal protein dynamics, Perez et al. [40] extended the diffusion in a sphere model and introduced a Gaussian distribution of sphere radii f(a) instead of a single sphere. The Gaussian distribution is defined as 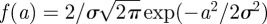, with the standard deviation σ as the free parameter. The mean value of the sphere radius is given by 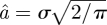. A neutron scattering study using specific isotope labelling in order to investigate the dynamics of specific amino acids in bacteriorhodopsin demonstrated the heterogeneity of internal protein dynamics [57]. The obtained average sphere radius 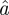increases from 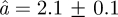Å at 16.9°C to 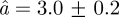Å at 36.9°C. The immobile fraction p has an average value of 0.50 and increases only slightly with temperature from p = 0.47 ± 0.02 at 16.9°C to p = 0.55 ± 0.01 at 36.9°C. Using the same model, we have quantified the average amplitudes of motion in concentrated Hb solution [8]. The average sphere radius was found to increase from 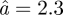Å at 6.9°C to 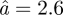Å at 36.9°C, while the immobile fraction was constant with temperature p = 0.38 [8]. Within the error bars the obtained average sphere radii of Hb in RBCs and of Hb in concentrated solution are similar when we exclude the value at 36.9°C, which is larger in Hb in RBCs than in the Hb solution. Although the energy resolutions of the instruments used for both experiments are different (17 and 100 µeV, respectively) the observed motions look similar. This might be either because the same motions are seen using the IRIS and the time-of-flight spectrometers or because different classes of motions in the order of 40 ps and several ps are similar. The second possibility would also imply that the corresponding hierarchical structures in the energy landscape are similar.

The model for diffusion in a sphere approximately describes the measured EISF. Better fits can be obtained when a Gaussian distribution of sphere radii is used. It should be noted that both the diffusion in a sphere model and the Gaussian distribution can only be simple and rough representations for the heterogeneity of internal protein dynamics. In any case, models are never wrong, they are just more or less appropriate.

5. Conclusion

In summary, we measured the global self-diffusion and internal dynamics of Hb in RBCs, in vivo, using high-resolution quasi-elastic neutron backscattering spectroscopy. It is demonstrated that global protein diffusion and internal dynamics can be separated and interpreted quantitatively. The cross over from the short- to the long-time limit of Hb self-diffusion could be observed. It is demonstrated that the diffusion of Hb at high concentration in RBCs can be described with concepts of colloid physics. Experimental data are in quantitative agreement with hydrodynamic theory of non-charged hard-sphere suspensions when it is assumed that the hydration shell moves with the protein. It is shown that interfacial protein hydration water has a strong influence on global protein diffusion under physiological conditions in cells. The same result was obtained by Doster & Longeville [14] using spin-echo spectroscopy. Experiments with whole RBCs using micropipette aspiration and colloidal osmotic pressure measurements [3,5] indicated that the cellular environment might have similarities to a colloidal gel. It was suggested that the trigger for the formation of the gel could be Hb–Hb interactions, which are influenced by the molecular properties of Hb [2,6]. Recently, we studied Hb–Hb interactions in concentrated solution using small-angle neutron scattering and showed that Hb molecules associate into a large-scale superstructure at high concentration [58]. In this article, we observe a slowing down of the atomistic diffusion of Hb, which might indeed lead to gel-like properties on a macroscopic scale. It is demonstrated how incoherent neutron scattering can contribute to the understanding of cellular phenomena on a macroscopic scale.

Internal Hb dynamics was also measured and could be separated from global Hb diffusion. The internal motions of Hb were compared with results obtained with hydrated powder and solution samples. Different types of motions were brought into focus by using neutron spectrometers with specific energy resolutions. Hydration water was found to have a strong influence on motions in the ps time scale. Jump-diffusion coefficients of internal Hb fluctuations are significantly enhanced and residence times of the internal diffusive jumps are reduced in RBCs as compared with fully hydrated Hb powder. Slower internal dynamics of Hb in RBCs in the ns time range were found to be rather similar to results obtained with fully hydrated protein powders, solutions and E. coli cells. Still missing is a combined analysis of the data measured with different spectrometers, which should be done in a future study. Future work might also be dedicated to investigating protein dynamics in whole cells under different environmental conditions.

Appendix A. Global Hb diffusion: contribution of rotational and translational diffusions

Global protein diffusion consists of translational and rotational protein diffusions around the centre of mass. Free translational diffusion is described by the scattering function

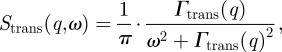A 1

with the diffusion coefficient Γ_trans(q) = D₀ · q² [41]. It was shown theoretically by Perez et al. [40] that rotational diffusion of a protein leads to an additional broadening of the measured HWHM. Rotational and translational diffusions of the protein are assumed to be uncorrelated. In that case, the scattering function of global protein diffusion S_G(q,ω) is the convolution of the scattering functions of translational and rotational diffusions

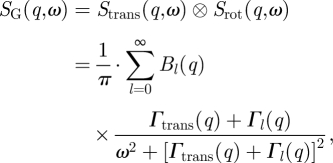A 2

with Γ_l = l (l + 1) · D_rot and the rotational diffusion coefficient D_rot [40]. The integrals in the terms B₀(q) and B_l(q) are extensions of the Sears [59] model for rotation on the surface of a sphere. They describe the distribution of hydrogen atoms within the protein

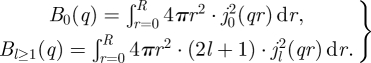A 3

The terms j_l are the lth-order spherical Bessel function of the first kind and R is the radius of the Hb. The terms B_l(q) were integrated numerically and the obtained scattering function S_G(q,ω) could be perfectly approximated by a single Lorentzian with the apparent diffusion coefficient D_app and the HWHM Γ_G(q) = D_app · q². The apparent diffusion coefficient D_app was compared with D₀, which gave the relation of D_app/D₀ = 1.27 [7,40].