Figure 2.
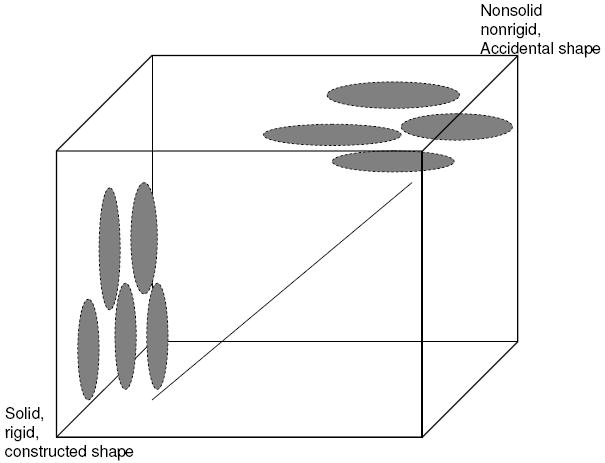
A hyperspace of categories. The ellipses represent categories with particular. generalization patterns (constrained in some directions but allowing variability in others). Packing Theory predicts that near categories in the space will have similar generalization patterns and that there should be a smooth gradient of changing category generalizations as one moves in any direction in the space. Past research shows that categories of solid, rigid and constructed things are generalized by shape but categories of nonsolid, nonrigid, and accidentally shaped things are generalized by material. Packing Theory predicts a graded transition in feature space between these two kinds of category organizations.
