Mechanistic Complexity in Organo–SOMO Activation

Singly occupied molecular orbital (SOMO) activation provides a pathway for asymmetric α-addition to aldehydes.[1] The scope of SOMO activation includes the allylation, enolation, vinylation, styrenation, chlorination, polyene cyclization, and arylation[2] of a range of aldehydes. This union of organocatalysis with single-electron oxidative coupling is an intricate process involving the complex balance of catalyst, oxidant, radicophile, base, temperature, heterogeneous reaction conditions, and H₂O. To examine the role of each component in this complex process, a series of spectroscopic and kinetic studies were carried out to study the asymmetric allylation of 1 shown in Equation (1).[1a] The data described herein show three important features: 1) Oxidation of the intermediate enamine is rapid and preferential to oxidation of the catalyst, 2) H₂O concentration is critical for catalytic efficiency, and 3) the kinetic role of ceric ammonium nitrate (CAN) is masked by a physical phase-transfer process.

(1)

The mechanism of the system is challenging to study since it is heterogeneous, but findings from initial work show that the presence of H₂O is important for reaction success.[1a] Additionally, one of the key design features of the process involves reaction of the catalyst (3) with the substrate to form an intermediate enamine that is preferentially oxidized in the presence of catalyst or substrate. Previous studies show that enamines[3] are more readily oxidized than amines.[4] To further explore the selectivity of the oxidation, a series of amines and enamines derived from imidazolidinone catalysts were studied using stopped-flow spectrophotometry in an attempt to determine the impact of the structure on the rate of a single-electron oxidation. A range of single-electron oxidants based on Ce^IV, Cu^II, and Fe^III were explored. In each case, enamine oxidation was faster than the mixing time of the stopped-flow spectrophotometer even at reduced temperatures (−10°C). Conversely, oxidation of the catalyst was slower than the time-scale of the stopped-flow system (1000 s). Although these findings did not provide the structure–reactivity relationships initially desired, they indicated that oxidation of the enamine is significantly more rapid under homogeneous conditions than oxidation of the catalyst.

Since the SOMO system is mechanistically complex, reaction progress kinetic analysis (RPKA) was employed to study the reaction in Equation (1). This approach, described by Blackmond, provides an elegant method for the study of mechanistic properties under synthetic conditions.[5] To utilize RPKA, two factors are necessary: 1) a detailed understanding of the stoichiometry of the reagents used, and 2) an understanding of the concept of excess. Excess (e) is defined as the difference in initial stoichiometric concentrations of a reagent (CAN) and the monitored substrate (1) [Eq 2].

$$[e]={[\text{CAN}]}_0-2{[\mathbf{1}]}_0$$ (2)

The “same excess” protocol[5] determines whether the active catalyst concentration remains constant throughout the reaction. Initially, the SOMO reaction (run 1, Table 1) was performed in the absence of H₂O with exhaustively dried reagents in excess with respect to 1 (0.25 M) and the free amine of 3 at 20 mol% loading (0.05 M). A second reaction was performed at the half-life of the SOMO system (run 1–50%, Table 1) using the same excess for all reagents with respect to 1 as in run 2, Table 1 and the same concentration of 3 (0.05 M). The two reactions were monitored starting 15 min after addition of 1 and were tracked until completion by gas chromatography (GC) through the drawing of aliquots from the reaction mixture. While GC analysis does not provide as high a data density as calorimetric or spectroscopic methods, these techniques were not amenable to the SOMO system due to its heterogeneity and timescale. An exponential function was fit to the decays produced from GC analysis to extract the kinetic properties of the SOMO system and the error was determined from the uncertainty in the fit (see the Supporting Information). All data that fit to first-order exponential decays display first-order kinetics in [1]. The results of these reactions are shown in Figure 1 as a plot of rate versus [1].

Table 1.

“Same excess” conditions for SOMO-activated reaction (1).

Run	[1]	[CAN]	[2]	[NaHCO3]	[3]	[4]
1[a]	0.250	0.600	0.625	0.375	0.050	0.000
1–50%	0.125	0.350	0.500	0.250	0.050	0.125
2[a]	0.125	0.350	0.500	0.250	0.050	0.000
3[b]	0.250	0.600	0.625	0.375	0.050	0.000
4[b]	0.125	0.350	0.500	0.250	0.050	0.000

^[a]Run under anhydrous conditions.

^[b]Run in the presence of 0.500M H₂O.

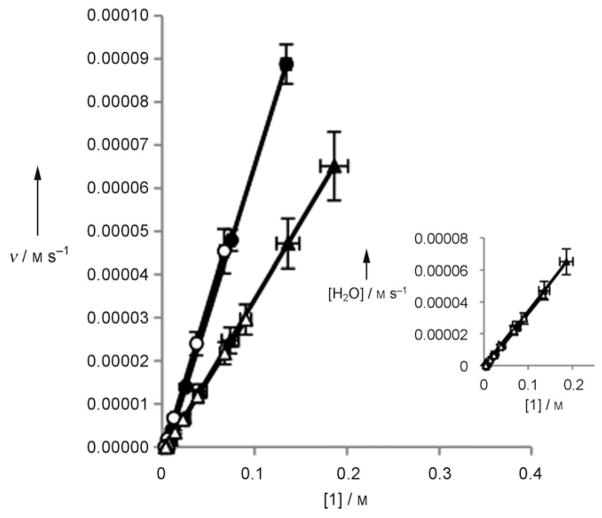
Figure 1.

Rate vs. concentration of 1 for anhydrous same excess experiments for run 1 (▲) and run 2 (△) and same excess experiments with H₂O for run 3 (●) and run 4 (○).

The runs under anhydrous conditions (1 and 2) do not overlay with each other. Under nondeactivating conditions, the two lines overlay because they represent the same reaction initiated at different points. The lack of overlay in this case indicates that runs 1 and 2 are not following the same kinetic profile, consistent with deactivation of 3. When the same excess reactions were repeated with two equivalents of H₂O (runs 3 and 4), the profiles overlay with each other (Figure 1), demonstrating that H₂O is vital for inhibiting the deactivation of 3. Additionally, the shapes of the decays in Figure 1 provide further insight into the mechanism. The straight lines observed for runs 3 and 4 under optimal conditions show a constant change in rate which is consistent with a first-order decay of 1. Run 1 has an initial linear decay, but the slope changes towards the end of the reaction. This varying slope of the curve is indicative of a higher-order process, which is consistent with a change in the concentration of 3 due to deactivation. Mathematical modeling of the process supports this supposition (see the Supporting Information). Run 2 has a constant change in rate because the run uses 40 mol% of 3. Under these conditions, each catalyst molecule is only used twice, providing insufficient opportunity to observe the impact of the deactivation through change in the concentration of 3. The observed change in rate for run 1 at the beginning of the reaction agrees with this assertion.

The use of H₂O in asymmetric organocatalytic reactions is well-established;[6] it ranges from substoichiometric quantities to the bulk medium in which reactions are performed. MacMillan et al. first observed that an addition of 5% H₂O increased the rate and enantioselectivity of imidazolidinone-catalyzed Diels–Alder reactions.[7] The groups of Ward[8] and Pihko[9] observed that the presence of at least one equivalent of H₂O improved yields in proline-catalyzed aldol reactions of ketones and aldehydes carried out in DMF. Pihko et al. observed that not only did H₂O appear to accelerate the rate of the reaction, but increasing H₂O concentrations also decreased a side reaction involving proline. Detailed mechanistic analysis by Blackmond et al. fully characterized the off-cycle process proposed by Pihko et al. and showed that H₂O reverses this side reaction, preventing deactivation of proline.[10] Additionally, the groups of Armstrong and Blackmond showed that while the active concentration of the catalyst is maintained by H₂O, it in fact suppresses the rate of the aldol reaction, possessing a reaction order of −0.7.[10]

To further elucidate the role of H₂O in organo–SOMO activation, its impact on enamine formation was examined outside the reaction conditions. When 1 and 3 were combined in dry, deuterated acetone, no enamine was observed by ¹H NMR spectroscopy over the course of 7 h (see the Supporting Information). A catalytic amount of dry CAN (3 mol%) was added resulting in an equilibrium of 1, 3, and enamine 5 (see Scheme 2). Addition of H₂O (2 equiv) shifted the equilibrium towards 1 and 3, greatly reducing the intensity of the signals belonging to 5. Further addition of H₂O eliminated detectable amounts of 5. These data show that H₂O impedes formation of 5. This observation in concert with the kinetic results explains the role of H₂O under activating conditions. While vital for maintaining the concentration of 3, H₂O hinders the rate of reaction. This dual role of H₂O was similarly reported for proline-catalyzed aldol reactions.[8]

Scheme 2.

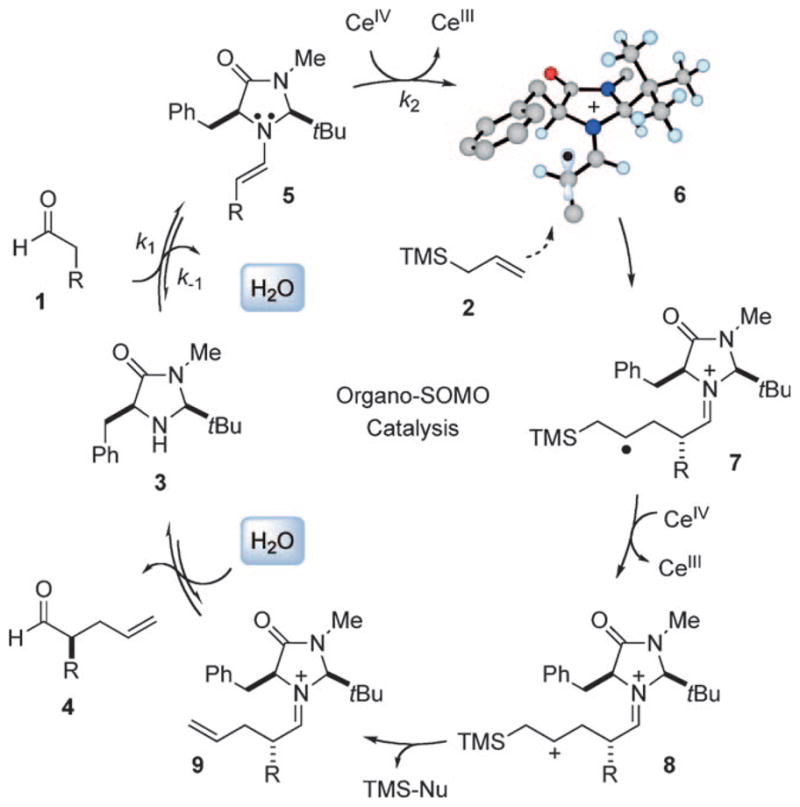
Proposed catalytic cycle for SOMO activation. The structure of 6 shown was obtained by DFT calculation.

Enamine 5 was not detected through GC analysis during the course of the reaction. To determine the stability of 5 using this method, two benchtop reactions were performed employing conditions different from those of the SOMO reaction: equivalent amounts of 1 and 3 were reacted in the presence of either CAN (3 mol%) or Ce(NO₃)₃·6H₂O (3 mol%). Both reactions provided 5 in isolable quantities demonstrating that both oxidation states of cerium are effective Lewis acids for enamine formation. Analysis of the GC data showed that 5 is detectable using this technique; however, its peak was not observed during reaction progress kinetic studies. This finding is consistent with the results of homogeneous rate experiments showing that 5 is oxidized immediately upon formation. As a consequence, 3, which is detected during the course of the reaction, is the resting state of the cycle and is not oxidized to any appreciable extent under reaction conditions.

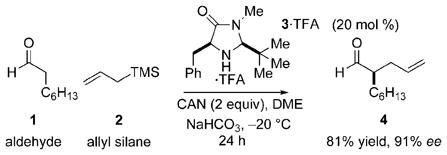
Having examined the formation of 5 and the impact of H₂O outside of the reaction conditions, it was necessary to assess the effect of the H₂O concentration on the rate of reaction utilizing a “different excess” experiment. This type of experiment allows for the determination of the reaction orders of both the substrate and the reagent in question.[5] Employing dried anhydrous reagents and solvent, a same excess experiment was performed in the presence of four equivalents of H₂O (runs 5 and 6, Figure 2). Clearly, the rate of reaction decreases with increasing H₂O content; however, the overlay of runs 5 and 6 in Figure 2 shows that the concentration of 3 remains constant. This finding is consistent with the behavior of other organocatalytic systems that proceed through enamine formation.[6] Additionally, the rates of runs 4 and 6 were multiplied by their respective constant concentrations of H₂O and plotted versus the concentration of 1 in the inset of Figure 2. Overlay in this plot indicates that the reaction is approximately inverse first order in H₂O. This rate order is similar to that of H₂O in proline-catalyzed aldol reactions.[8b]

Figure 2.

Rate vs. concentration of 1 for studying the effect of H₂O on the reaction rate for runs 3 (●), 4 (○), 5 (▲), and 6 (△); and (inset) rate/[H₂O] vs [1] for determining the rate order of H₂O for runs 3 (●), 4 (○), 5 (▲), and 6 (△).

Next, the rate orders of the other species in solution were deduced using the same method. Under reaction conditions similar to those of run 4, three separate reactions were performed in which the concentrations of CAN, NaHCO₃, and 3 were changed, respectively, the results of which are given in Table 2. These data show that the reaction is approximately first order in 3 and that CAN and NaHCO₃ show zero-order behavior. This observation for CAN is unexpected; however, solid CAN is observed in the reaction mixture throughout the entire process, suggesting that the solution is saturated in oxidant. As a consequence, it is possible that the true kinetic role of CAN is masked by a physical phase-transfer process that controls the concentration of CAN in solution. If this supposition is correct, addition of excess CAN will not increase the concentration of CAN in solution. As a result, no observable effect on the rate of reaction will be detected. To test this, the solubility of CAN was examined under reaction conditions in the absence of 1 using UV/vis spectroscopy. In the absence of H₂O, the concentration of CAN in the solution is 0.03M. However, upon addition of H₂O (2 equiv), [CAN] increases to 0.39 M. It is important to note that these values are most likely the upper limits of CAN solubility at −20°C. The SOMO reaction is run in a highly concentrated slurry (Table 1) and is assembled at −78°C, a temperature at which CAN is totally insoluble. When the system is warmed to reaction temperature, CAN is in competition with 1, 2, 3, and NaHCO₃ for available solvent.

Table 2.

Rate orders of CAN, NaHCO₃, 3, and H₂O.[11]

Entry	1	2	3	4
Reagent	CAN	NaHCO3	3	H2O
Order	0	0	1	−1

Taken together, the kinetic and NMR studies yield the following results: 1) The rate of reaction is approximately first order in 1 and 3 as well as inverse first order in H₂O under optimal conditions for catalysis. 2) At low concentrations of H₂O (below 2 equiv), the catalyst is deactivated. 3) Zero-order kinetics are observed for CAN and NaHCO₃. 4) Under reaction conditions, it is possible that the concentration of CAN in solution remains constant through the course of the reaction due to its limited solubility. 5) Intermediate enamine 5 is not detected by GC analysis during the course of the reaction. The question that remains is: Could the oxidation of 5 be rate-limiting despite the zero-order kinetics obtained for CAN? Scheme 1 shows the initial two steps of the reaction for the formation of enamine 5 and its subsequent oxidation. Equation (3) is the expression for the overall rate of reaction.

Scheme 1.

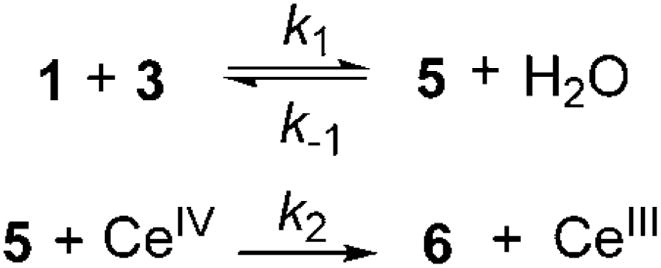
Equilibrium of enamine formation coupled with single-electron oxidation through Ce^IV.

$$-\frac{d[\mathbf{1}]}{dt}=\frac{k_1{k}_2[\mathbf{1}][\text{CAN}]}{k_{-1}[{\text{H}}_2\text{O}]+k_2[\text{CAN}]+k_1[\mathbf{1}]}{[\mathbf{3}]}_{\text{total}}$$ (3)

If the reaction is zero order in CAN, 3 is the resting state of the cycle, and the formation of 5 is rate-limiting, the final rate equation is Equation (4). This equation is inconsistent with

$$-\frac{d[\mathbf{1}]}{dt}=k_1[\mathbf{1}]{[\mathbf{3}]}_{\text{total}}$$ (4)

kinetic results showing the reaction is inverse first order in H₂O. If we assume that the oxidation of 5 is rate-limiting and that k₁[1] ≪ [1] (because 3 is the resting state of the cycle), Equation (3) simplifies to Equation (5). Under optimized

$$-\frac{d[\mathbf{1}]}{dt}=K_{\text{eq}}{k}_2\frac{[\mathbf{1}][\text{CAN}]}{[{\text{H}}_2\text{O}]}{[\mathbf{3}]}_{\text{total}}$$ (5)

reaction conditions, RPKA shows the change in rate with respect to [1] is constant, which is consistent with constant [3]_total, [Ce^IV], and [H₂O] throughout the reaction, providing the straight line defined by Equation (6).

$$-\frac{d[\mathbf{1}]}{dt}=k_{\text{obs}}[\mathbf{1}]$$ (6)

Scheme 2 provides a graphical representation of the full catalytic cycle based on the mechanistic analysis described above. Reaction of 3 with one equivalent of 1 produces enamine 5 and an equivalent of H₂O. The equilibrium is shifted towards 5 by the Lewis acid (Ce^IV or Ce^III) and is reversed by H₂O. The enamine is then oxidized by Ce^IV to give radical cation 6 as the rate-limiting step. Coupling of 2 and 6 produces intermediate 7. A second equivalent of Ce^IVoxidizes 7 to 8, which undergoes β elimination of the silyl cation through reaction with a nucleophile present in solution according to a known nucleophilic displacement mechanism,¹² providing iminium intermediate 9. Finally, 3 is released by the addition of one equivalent of H₂O to 9, generating product 4 and a proton which must be absorbed by a base to prevent protonation of 3.

The catalytic mechanism of Scheme 2 ideally only requires one equivalent of H₂O which is generated upon formation of 5 and consumed through hydrolysis of 9. The final question that remains is: Why are two equivalents of H₂O necessary for optimal catalytic efficiency? CAN is oxophilic and hydrophilic, so it is likely that H₂O produced during the course of the reaction under anhydrous conditions is sequestered through coordination to the metal, preventing release of 3. This coordination is typified by a dark red color which is observed when two equivalents of H₂O are added to the reaction mixture.[13] Under anhydrous conditions, the color is far weaker due to the order of magnitude decrease in available H₂O. Excess H₂O also plays a significant role in maintaining the limiting amount of soluble CAN necessary for the oxidation of 5. Under anhydrous conditions, CAN has limited solubility. Addition of H₂O to the slurry of CAN under reaction conditions increases the homogeneous concentration through coordination to the metal. It is this coordination that removes H₂O from the catalytic cycle. While further addition of H₂O increases the solubility of CAN, it reverses the formation of 5, thereby decreasing the rate of the reaction.

From a practical standpoint, these findings imply that the reaction can be optimized by carefully drying reagents and titrating a known amount of H₂O into the system. To test this supposition, a reaction was run where all reagents and the solvent dimethoxyethane (DME) were thoroughly dried. Before initiation of the reaction, H₂O (2 equiv) was added. This method resulted in a significantly shorter reaction time (8 h) and an increase in yield (89%, 86% ee).[1a]

Overall, these studies demonstrate the inherent mechanistic complexity of the SOMO catalysis. Utilization of RPKA in conjunction with spectroscopic studies allowed for the detailed determination of the kinetic properties of a reaction containing organocatalysis, phase transfer, single-electron oxidation, and free-radical chemistry. Additionally, this work, in concert with the studies of the groups of Blackmond and Armstrong on the proline-catalyzed aldol reaction[10] and the recent work of Wennemers et al. on organocatalytic conjugate additions,[14] shows that a thorough understanding of the role of H₂O is necessary for all organocatalytic processes that proceed through an enamine intermediate, regardless of the catalyst structure and the nature of the major bond-forming event. We are currently examining the mechanism of other SOMO-activated processes to further understand the effect of solvent and H₂O on the phase-transfer process that controls the homogenous concentration of the oxidant. The results of these studies will be reported in due course.

Experimental Section

DME was dried over sodium benzophenone ketyl. 1, 3, CAN, and NaHCO₃ were dried through azeotropic removal of H₂O with benzene. 2 was dried using activated 3 Å molecular sieves. Dried solvents and reagents were stored in a drybox containing an Ar atmosphere and a platinum catalyst for drying. Detailed experimental protocols are contained in the Supporting Information.