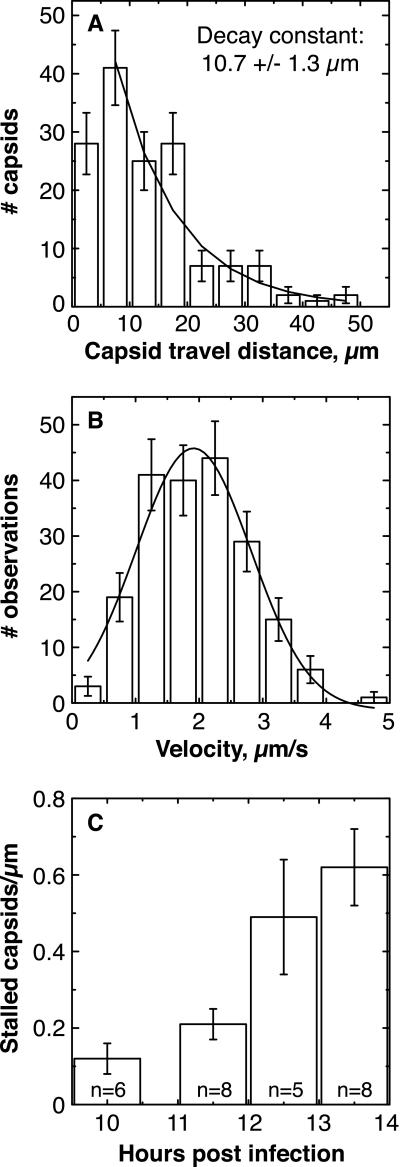
Figure 3.

Analysis of capsid movement. (A) Histogram of lengths of anterograde runs. Error bars are expected uncertainty, assuming Gaussian statistics N). The smooth curve is the best fit decaying exponential (reduced χ² = 1.24; P = 0.28); bin 1 was excluded from the fit because our temporal resolution was insufficient to resolve short runs. An exponential distribution is consistent with processivity-determined runs. The maximum length of observed runs was experimentally limited by the size of the observation window (30–50 μm). (B) Histogram of velocities of anterograde runs. Each data point used in the histogram was the average velocity of a moving capsid, calculated by dividing the spatial length of the run by its temporal duration. Error bars are expected uncertainty, assuming Gaussian statistics 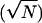. The smooth curve is the best fit Gaussian (reduced χ² = 1.02; P = 0.40) with a mean of 1.979 ± 0.063 μm/s and a width of 1.621 ± 0.121 μm/s. (C) The number of stalled capsids per micrometer of axon increased with time postinfection. This number was determined by examining approximately 30 μm of each axon during an entire recording, usually approximately 2 min in duration. The n value in each bar is the number of different axons examined. Error bars indicate the experimentally determined standard error. Early data were pooled, resulting in the uneven spacing of bars along the abscissa.