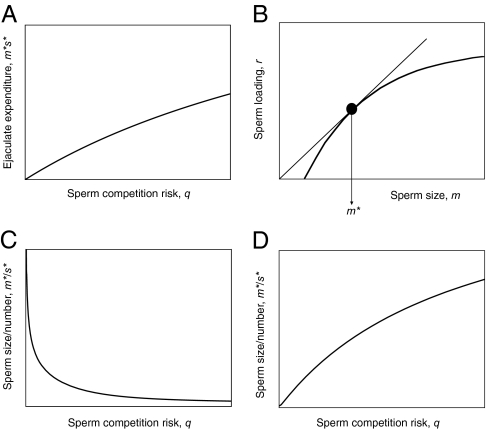
Fig. 1.

Theoretical predictions for sperm size–number relationship with increasing risk of sperm competition. (A) The ESS total sperm expenditure (product of sperm size and number, m*s*) always increases across the risk range sperm competition risk, q, as observed in passerine birds and Drosophila (Fig. 3 A and B). (B) Sperm loading factor, r, determines a sperm’s competitive ability and must increase at a decreasing rate with m. The tangent to the curve r(m) gives the marginal value theorem solution for ESS sperm size, m*, at a given level of sperm competition risk, q. If sperm density increases the intercept of r(m), or decreases its slope, a higher ESS sperm size is generated. (C) The “default expectation” (as observed in passerine birds; Fig. 3C)—a decreasing relationship between the ratio of sperm size/number, m*/s*, and sperm competition risk, q, is expected when (i) r(m) is unaffected by the sperm density, or where (ii) increasing sperm density decreases the intercept of r(m) or increases the slope of r(m), or where (iii) increasing sperm density only generates weak increases in the intercept of r(m) or weak decreases in the slope of r(m). (D) An increasing relationship between the ratio of sperm size/number, m*/s*, and sperm competition risk, q (as observed in Drosophila; Fig. 3D), is expected only when increasing sperm density sharply decreases the slope or increases intercept of r(m) and is more likely to occur in sperm displacement systems such as those found in insects.