Electrostatic Clustering and Free Energy Calculations Provide a Foundation for Protein Design and Optimization

Abstract

Electrostatic interactions are ubiquitous in proteins and dictate stability and function. In this review, we discuss several methods for the analysis of electrostatics in protein–protein interactions. We discuss alanine-scanning mutagenesis, Poisson–Boltzmann electrostatics, free energy calculations, electrostatic similarity distances, and hierarchical clustering of electrostatic potentials. Our recently developed computational framework, known as Analysis of Electrostatic Similarities Of Proteins (AESOP), incorporates these tools to efficiently elucidate the role of electrostatic potentials in protein interactions. We present the application of AESOP to several proteins and protein complexes, for which charge is purported to facilitate protein association. Specifically, we illustrate how recent work has shaped the formulation of electrostatic calculations, the correlation of electrostatic free energies and electrostatic potential clustering results with experimental binding and activity data, the pH dependence of protein stability and association, the design of mutant proteins with enhanced immunological activity, and how AESOP can expose deficiencies in structural models and experimental data. This integrative approach can be utilized to develop mechanistic models and to guide experimental studies by predicting mutations with desired physicochemical properties and function. Alteration of the electrostatic properties of proteins offers a basis for the design of proteins with optimized binding and activity.

Introduction

Electrostatic interactions play a key role in many biological processes.10,26,42,44,49 Proteins are comprised of ionizable amino acids, which contain titratable groups whose ionization states are dependent on their physicochemical properties and the physicochemical properties of the surrounding environment. The distribution of whole and partial charges throughout the three-dimensional structure of a protein determines its electrostatic properties, and governs how the protein will interact with its binding partners. It is well known that several intermolecular forces, including van der Waals, hydrophobic, and electrostatic interactions, contribute to association and stability of protein complexes. For excessively and oppositely charged proteins, association is divided into recognition and binding, according to the two-step model (Fig. 1a).25,28,38,49 In the recognition step, long-range electrostatic interactions cause electrostatic steering, accelerating the formation of an encounter complex and orientation of complementary binding sites. In the binding step, the protein interface is desolvated and side chains are optimally rearranged through short-range interactions (polar and nonpolar) to stabilize the bound complex.

FIGURE 1.

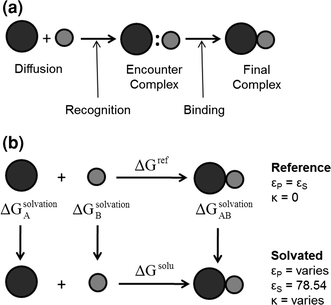
(a) Scheme illustrating the two-step model of protein association. (b) Thermodynamic cycle for calculation of electrostatic free energy of association and solvation. The top horizontal process represents association in a reference state (without water and ions) and the bottom horizontal process represents association in a solvated state in the presence of ions. Three vertical processes show solvation of each free protein (A and B) and the protein complex (AB). The dielectric coefficients ε_p and ε_s correspond to protein and solvent, respectively. The ion accessibility parameter, κ, depends on ionic strength

In recent years, computational methods have rapidly evolved and become an integral part of the analysis of protein–protein interactions. Depending on the accuracy of the underlying physics, algorithm efficiency, and parameterization, computational techniques can provide an excellent complement to experimental techniques and methods. Since the advent of computational analysis of proteins and their interactions, researchers have shown interest in developing methods to accurately calculate electrostatic forces between proteins. Molecular dynamics (MD) simulations1,12,26,45 often incorporate explicit solvation, in which proteins are surrounded by water molecules and ions. These complete atomistic models offer an accurate picture of the electrostatic forces and energetics involved in protein–protein interaction, but are computationally expensive, especially for large systems. Alternatively, implicit solvation models offer a more efficient analysis of electrostatics, since solvent molecules are not explicitly modeled and dynamic effects are not directly incorporated.1,11,12

In this review, we present an overview of a new computational framework for electrostatics calculations. This review is not intended to be comprehensive in nature and focuses mainly on improvement, validation, and application of electrostatic calculations from work in our group, with representative applications. Our Analysis of Electrostatic Similarities Of Proteins (AESOP)24 computational framework incorporates alanine-scanning mutagenesis, Poisson–Boltzmann (PB) electrostatics, electrostatic free energy calculations, and hierarchical clustering in an effort to understand and compare the electrostatic nature of protein families, including homologs and mutants. We present herein the computational basis for AESOP, and specific applications that exemplify its predictive capability for protein design and optimization.

Methods

Alanine-Scanning Mutagenesis

Our computational methods for evaluation of electrostatics begin with an atomic-resolution three-dimensional structure of a protein or protein complex. Structures are obtained from the protein data bank (PDB),4 as determined by either X-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy. For proteins without an experimentally determined structure, we can use homology modeling to model the structure of the protein based on a sequence alignment using proteins with known structure and similar sequence as templates. Two most convenient criteria for similarity are (a) an identity of at least 25% for a sequence size greater than 100 amino acids and (b) an expectation (E) less than 10⁻⁴, which gives the likelihood that similarities are due to chance.29

Alanine-scanning mutagenesis has long been regarded as an important experimental tool in probing protein function by delineating the contribution of the mutated amino acids in specific biological processes. In AESOP, we use computational alanine scans to observe the effects of specific ionizable amino acids on the electrostatic potential distribution and associative properties of proteins and protein complexes. Mutations of charged residues at physiological pH (arginine, lysine, glutamic acid, aspartic acid, and histidine) to alanine introduce perturbations in the electrostatic potential distribution of the protein, with minor alterations in protein structure or integrity. AESOP utilizes the R software package36 for structure editing, calculation, and electrostatic analyses. AESOP performs alanine mutations by simply removing the side chain atoms of ionizable residues, with the exception of Cβ. For electrostatics calculations, we typically limit alanine scans to mutants of ionizable residues only, since these mutations have the largest effects on Coulombic interactions and electrostatic potentials. However, AESOP can be used to analyze mutation of any residue to alanine, since dipole moments and partial charges can alter the distribution of electrostatic potential. In addition, mutation of any residue can affect the shape of the dielectric and the ion accessibility surfaces of the proteins (see below). Besides alanine, mutations to any other residue are also possible.

PB Electrostatics

PB calculations represent the forefront of electrostatic analysis using implicit solvation in proteins.2,19,26 Since solvent molecules and ions are not explicitly modeled, PB calculations can efficiently determine electrostatic potential distributions and electrostatic free energies of proteins. AESOP utilizes the grid-based Adaptive PB Solver (APBS)3 for all electrostatics calculations. At low ionic strengths (including physiological ionic strength of 150 mM), the linearized PB equation provides a sufficient approximation for the calculations of electrostatic potentials of proteins, given by (in SI units):

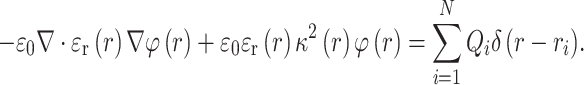1

In Eq. (1), φ(r) is electrostatic potential in units of k _B T/e (k _B the Boltzmann constant, T the absolute temperature, and e the magnitude of electron charge), ε _r(r) the dielectric coefficient (relative electrostatic permittivity with respect to vacuum), ε ₀ the electrostatic permittivity of vacuum, κ ²(r) the ion accessibility parameter for ±1 counter ions (related to a modified inverse Debye screening length), Q _i the fixed protein ith charge at atom position r _i (to a total of N charges), and the δ function denotes the position of charges. The ion accessibility parameter allows for the incorporation of ionic strength into the calculation of electrostatic potential. In PB calculations, dielectric coefficient, ion accessibility, and charge must be defined at each grid point, in order to solve for electrostatic potential. Charges are assigned based on the atomic structure, and dielectric and ion accessibility values are assigned based on solvent accessible and ion accessible molecular surfaces, respectively. Typically, the solvent and ion accessible surfaces are calculated by the union of the center points of spherical probes with 1.4 and 2.0 Å radii, corresponding to the molecular radii of water and ions, respectively.

PB calculations are highly sensitive to parameter selection. Previous analyses have shown that free energy values calculated using PB electrostatics vary significantly with protein dielectric and choice of dielectric boundary,13,15,39,42,43 thus it becomes important to determine the proper selection of parameters, based on the application. In addition, since proteins are calculated in a discretized space, electrostatic potential calculations are sensitive to grid resolution.15

Electrostatic Similarity and Clustering

It is of interest to compare the distribution of electrostatic potential for different proteins. It is a well-known principle of biochemistry that protein structure is directly related to function. AESOP is centered on the idea that electrostatically similar proteins will have similar associative properties, and in turn will yield a similar biological function. Many methods of comparing electrostatic properties of molecules have been developed, and recently applied to proteins. Carbo et al. 6 developed a similarity index to compare the electron density of small molecules. More recently, additional electrostatic similarity indices (ESIs) by Hodgkin and Richards,18 Reynolds et al.,37 and Petke34 have been developed to compare the electrostatic potential distribution of two molecules.

While ESI measures were originally developed for the comparison of small molecules, Wade et al. adapted the measures and paved the way for application to proteins.5,47,50,52 Certain issues arise when dealing with such large biomolecules, most importantly how to treat the protein interior. Large or globular proteins tend to have polar character on their surfaces, whereas the interior or core is largely hydrophobic in nature due to solvent exclusion. When very low dielectric coefficients are used to model the protein interior, the electrostatic potential values in that region are much larger than observed outside the protein. Some similarity indices are highly sensitive to large values in the protein interior, and thus give disproportionate weight to these values. Wade et al. proposed the use of a skin region (Skin) when comparing grid points for calculation of similarity indices,47 such that only those values of electrostatic potential that fall between a radius of 3–7 Å from the protein surface are included in the calculation. This comparative scheme eliminates electrostatic potential values inside the protein, as well as those outside the Debye length (~7 Å at 150 mM ionic strength), which are thought not to have a significant effect on protein–protein association. Our group has examined the efficacy of a shell comparative scheme (Shell), which includes all potential values outside the solvent-accessible surface of the protein, and a whole-box scheme (WB), which includes all potential values calculated within the entire grid.22 The results of our analysis are discussed below.

In order to compare proteins and protein mutants based on electrostatic potential distribution and electrostatic similarity, AESOP utilizes hierarchical clustering21 with average linkage to generate dendrograms of mutants for comparison. ESIs (discussed above) are converted to electrostatic similarity distances (ESDs), in which identical electrostatic potentials have ESD = 0, with ESD increasing with increasing dissimilarity.

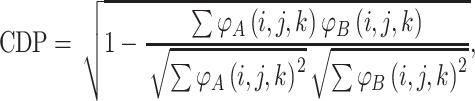2

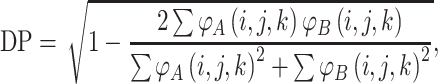3

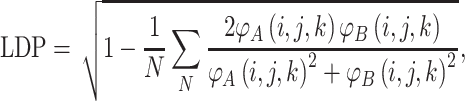4

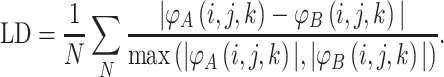5

In Eqs. (2)–(5), φ _A(i,j,k) and φ _B(i,j,k) represent the calculated electrostatic potential at grid point (i,j,k) for two compared proteins (A and B), respectively, and N represents the total number of grid points used in electrostatic calculations. The equations above compare dot products (correlation dot-product: CDP; dot-product: DP; and localized dot-product: LDP) and difference (localized difference: LD) with different normalizations, according to the ESIs mentioned above.5,6,18,34,37,47 The ESDs given above are used in AESOP to cluster mutants and homologous proteins based on electrostatic similarity,22 and a comparative analysis of their application is discussed later.

Free Energy Calculations

PB electrostatic potential calculations can easily be translated into electrostatic free energy values for proteins. APBS calculates free energy based on the distribution of electrostatic potential within and surrounding the protein, according to:

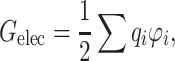6

where q _i and φ _i are the charge and electrostatic potential at each grid point, respectively. For protein complexes for which an atomic-resolution structure is available, we can calculate association free energy values based on a thermodynamic cycle, shown in Fig. 1b. Intuitively, protein association can be represented by the bottom horizontal process (ΔG ^solu), with solvent (ε _S = 78.54) and ionic strength (I = 150 mM) being modeled. It is well known that while electrostatic interactions between proteins are often favorable, their stabilizing effect is counterbalanced by desolvation.17 The effects of desolvation of each free protein and complex are incorporated into free energy calculations via the vertical processes in Fig. 1b. The top of the cycle depicts each protein and their association in a reference state (ΔG ^ref), in which solvent and ions are not modeled. In order to incorporate the effects of both association and solvation, ΔΔG ^solvation values are calculated, which incorporate both horizontal binding and vertical solvation processes. The described free energy values are calculated according to:

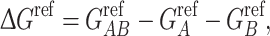7

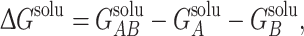8

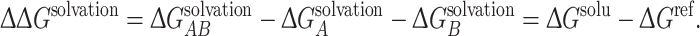9

Since APBS uses a grid-based method to solve the linearized PB equation, whole and partial atomic charges in the protein are distributed to neighboring grid points for calculation. This discretization can lead to self-energies and grid artifacts. In order to separate free energies into association and solvation components, care must be taken to eliminate grid artifacts and erroneous self-energies that arise as a result of numerical solution of the PB equation. Subtraction of the top horizontal process (reference state) from the bottom horizontal process (solvated state) will likely cancel these artifacts, presuming the structures of the separated components and their positions within the grid are identical to their respective coordinates in the complex in each case. In order to accurately calculate free energy of association in a solvated state, the APBS external program Coulomb is typically used to calculate nongrid-based free energy of each protein based on Coulombic potential, according to:

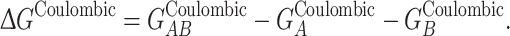10

An adjusted free energy quantity can be calculated for association in a solvated environment by incorporating nongrid-based Coulombic energy calculations, as shown below:

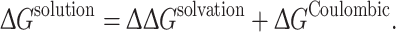11

The free energy values in Eqs. (9)–(11) are incorporated into AESOP to compare the relative association of proteins and protein mutants, in the absence of erroneous self-energies and grid artifacts.9,15 PB free energy calculations represent a method of quantitatively predicting biological activity, which is an important factor in the design and optimization of proteins.

Applications

Protein Design Using Electrostatics

Based on the two-step model for protein association, it can be reasoned that mutations that alter the electrostatic character of a protein can have a dramatic effect on binding without resulting in substantial structural changes. This hypothesis is based on the essential role of long-range electrostatic interactions during recognition of excessively and oppositely charged proteins, and has major implications for protein design. By utilizing this hypothesis and the perturbative methods of the AESOP framework, it is possible to computationally design protein analogs with tailored associative properties. We applied this approach to the design of novel analogs of the viral protein, VCP,41,52 which is an important example of viral mimicry used for immune system evasion. VCP is the complement control protein (CCP) of the vaccinia virus, and is composed of four excessively charged CCP modules. CCP modules are small compact domains consisting primarily of beta-sheets, which are stabilized by two disulfide bonds. CCPs are typically composed of multiple CCP domains connected by flexible linkers. VCP is capable of mimicking human complement regulators to initiate factor I-mediated degradation of C3b, one of the central proteins of complement activation. VCP has a highly related homolog, SPICE, which is produced by the more potent variola (smallpox) virus. Despite having a nearly identical sequence that differs by only 11 amino acids, VCP and SPICE differ by up to 1000-fold in their ability to regulate the complement system. In order to rationalize this significant gain in function, we computationally generated a series of VCP analogs based on charged amino acid substitutions found in SPICE. Simple Coulombic calculations were initially used to determine the effect of the mutations on the electrostatic potential of VCP, and visual comparison was used to identify analogs predicted to have function similar to SPICE.41 Experimental binding and functional assays were performed and confirmed the predicted activities of a series of 12 computationally predicted constructs.41 Among them, a VCP analog consisting of only two glutamic acid-to-lysine mutations was found to have similar activity to SPICE. A more rigorous analysis, including MD simulations, PB electrostatics, ESD clustering, covariance analysis of correlated and anti-correlated modular motions, and apparent pK_a calculations, was also performed to further elucidate the correlations between the overall positive charge of VCP and binding ability.52 The clustering results comparing the VCP analogs and SPICE reconfirmed our earlier predictions that changes in the electrostatic potential of VCP are responsible for the improved function of SPICE.52

We have also applied this design approach to the study of another CCP, Kaposica of Kaposi’s sarcoma-associated herpesvirus, which has a function similar to VCP and SPICE.35 In this analysis, we used homology modeling to generate a structure for Kaposica, which was used to analyze the electrostatic potential of the entire protein and each of the four CCP modules individually. PB electrostatic calculations were used to design a series of mutants with the goal of altering the overall positive potential of Kaposica or of each of its modules and linkers. One novel approach employed in the design of Kaposica analogs included charge reversal of individual CCP modules, which was used to elucidate the importance of the electrostatic character of each module. This was achieved by performing PB electrostatic calculations on each CCP module alone to determine which combination of basic-to-acidic mutations would produce a predominantly negative spatial distribution of electrostatic potential, while introducing the fewest changes. These electrostatic calculations guided experimental studies in which the designed analogs were synthesized and analyzed. The binding ability of the Kaposica analogs was evaluated using surface plasmon resonance, while factor I cofactor activity for C3b/C4b and C3-convertase decay accelerating activity were measured to examine the functionality of each analog. Comparison of electrostatic calculations and experimental data provided evidence in support of the importance of the electrostatic potential of individual CCP modules, and the use of electrostatic calculations in protein design.

Validation and Improvement of Electrostatics Calculations

Due to the complexity of biomolecular electrostatics, several assumptions and approximations, such as implicit solvation as discussed above, are often used. Another such approximation that is often made when performing electrostatic perturbation calculations is to ignore the effects of dynamics before and after mutation. To evaluate the effects of dynamics on electrostatic calculations of the AESOP framework, we performed an analysis on the barnase–barstar complex which incorporated alanine-scanning mutagenesis, electrostatic clustering and free energy calculations, as well as MD simulations.22 Since ionizable residues are typically solvent exposed, structural changes following mutation are expected to only occur locally and are therefore considered to be negligible. However, we observed that slight structural rearrangements in the barnase–barstar complex, which occurred during a 10-ns MD trajectory, resulted in ~100 kJ/mol difference in the solvation free energy of association. In contrast, we also observed that the conformation of the parent structure had little to no effect on the correlation of free energies of association with experimental binding abilities nor on the clustering results, since each mutant was compared relative to the same starting structure. Post-mutation relaxation, incorporated by using 5 ns MD simulations for each experimentally tested mutant, only provided minor improvement in the correlation of free energies of association with experiment. This study showed, at least for the barnase–barstar complex, that a rigid-body assumption is reasonable.

In addition to dynamic relaxation considerations, the selection of parameters in PB calculations is a subject of controversy in protein electrostatic analysis, particularly how to treat the protein interior. Researchers have reported the use of internal protein dielectric coefficients ranging between 2 and 40, and sometimes higher depending on the system.42 Other groups have suggested the use of a radially dependent dielectric function, in which a very low value is used to represent the central core of the protein, and values become higher toward the protein surface.33,43,48 Recently, we performed PB free energy calculations using dielectric coefficients of 2, 10, 20, and 40 for the protein interior.15 In addition, we examined the effects of ionic strength, PB linearization, and grid resolution on calculated free energy values. We calculated ΔG ^Coulombic, ΔG ^solution, and ΔΔG ^solvation values for alanine mutants of five different protein complexes with available experimental binding and kinetic data, obtained from the Alanine Scanning Energetics Database.46 These complexes represent a diverse dataset, varying in size, net charge, and biological function. Our results showed that for excessively and oppositely charged proteins, both ΔG ^Coulombic and ΔΔG ^solvation values correlated well with experimental data for all values of protein dielectric. Solution free energy values typically did not correlate well at low protein dielectric (ε_P = 2), but the correlation increased significantly as protein dielectric was increased. The strongest correlations were observed using ε_P = 40, which provides support for using higher dielectric values (ε_P ≈ 20–40), particularly for calculations involving protein complexes. The higher dielectric coefficient likely accounts for the highly polar protein interfaces that become buried upon complex formation, as well as minor structural rearrangements and surface alterations upon mutation. Our data also showed that Coulombic energies usually performed comparably to PB free energies, suggesting the use of ΔG ^Coulombic as an efficient initial predictor of relative protein association.15

Finally, we evaluated several comparative grid schemes (WB, Shell, and Skin) and ESD measures that have been proposed for electrostatic clustering analysis.22 We performed a thorough comparison of nine comparative grid scheme/ESD combinations for the electrostatic clustering of barnase alanine-scan mutants. Since free energies of association are the good predictors of binding ability, the clustering methods that are able to closely group mutations with similar free energies of association are thought to provide the best predictions in the absence of a cocrystal structure. Figure 2 contains dendrograms for the clustering of barnase mutants based on four clustering methods, and the colored circles indicate the relative free energy of association for each mutant. Inspection of these dendrograms shows that WB–DP is unable to properly cluster mutants with similar predicted effects on binding, while the remaining three methods perform equally well. This is due to the fact that DP relies on taking the product of electrostatic potential values, which gives disproportionate weight to values in the low-dielectric region of the protein interior, rather than the region of interaction outside the solvent-accessible surface of the protein. The WB–LD method provides accurate predictions without needing to define skin boundaries, and therefore provides a simpler and more efficient approach. Also, it should be noted that in this study, we used single-alanine mutations, which introduce small changes in electrostatic potential distribution, but may have substantial effects on binding depending on the location of the residue substitution. The results from such a comparison based on the electrostatic clustering of homologous proteins, which include multiple mutations and sometimes low sequence identity, may be quite different due to a substantial increase in the differences between electrostatic potentials.

FIGURE 2.

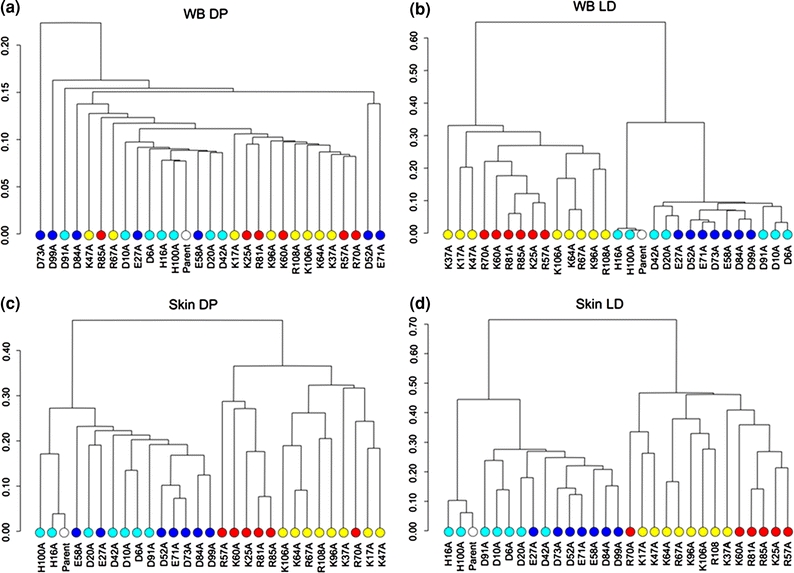
Dendrograms for the electrostatic clustering of barnase alanine-scan mutants based on: (a) WB–DP; (b) WB–LD; (c) Skin–DP; and (d) Skin–LD. Electrostatic potentials were calculated using ionic strengths corresponding to 0 mM ion concentration and ε_P = 2. Colored circles indicate the free energy change upon mutation for each alanine mutant relative to the parent (white circle). The color code is as follows: red for −500 to −201 kJ/mol, yellow for −200 to −1 kJ/mol, cyan for 1 to 200 kJ/mol, and blue for 201 to 400 kJ/mol

Clustering and Free Energy of Single-Alanine Mutants

Our group has utilized AESOP for clustering and free energy calculations of numerous systems, particularly protein complexes involved in complement immunity, including unpublished work. A specific example of clustering and free energy calculations involves EfbC and Ehp, proteins secreted on the surface of Staphylococcus aureus which contribute to immune evasion by the bacterium. Both proteins bind complement fragment C3d, and disrupt several processes in complement immune activation and regulation.14,40 Since EfbC and Ehp are excessively basic (+7e and +11e) and bind to an acidic region on C3d, electrostatics is shown to strongly influence association. The results of our work for C3d–EfbC are shown in Fig. 3.14 It is evident that mutations of acidic residues to alanine (acidic mutants) and basic residues to alanine (basic mutants) cluster together, respectively. In addition, we observe a high degree of correlation between clustering and free energy (ΔΔG ^solvation), as free energy values are similar within each cluster in the dendrogram. Our results also show that mutations located away from the protein–protein interface can significantly enhance complex association, suggesting that the global distribution of electrostatic potential surrounding the protein will govern the formation of an encounter complex between C3d and EfbC. In addition, our analysis with EfbC-homolog Ehp indicates that electrostatic potential may be responsible for its increased potency (based on experimental data)16 compared to EfbC. We plan to utilize our initial electrostatic analysis of C3d–EfbC and C3d–Ehp in the design of a therapeutic to combat S. aureus infection.

FIGURE 3.

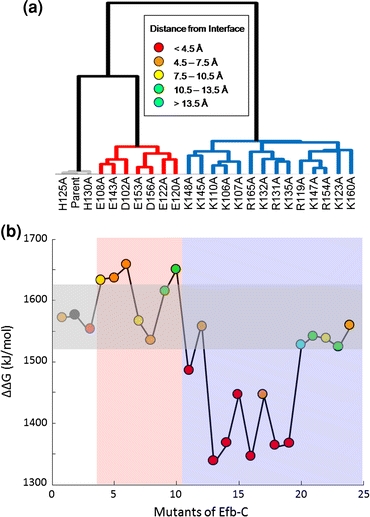
Clustering and free energy results for C3d–EfbC. (a) Clustering of EfbC mutants at 0 mM ion concentration and ε_P = 2. The color of the line to each mutant in the dendrogram indicates the type of mutation. Mutations of positive amino acids are in blue, mutations of negative amino acids are in red, and mutations of neutral amino acids are in gray. (b) Free energy (ΔΔG ^solvation) values of C3d–EfbC complex mutants at 0 mM ion concentration and ε_P = 2. The white, red, and blue vertical regions correspond to the line coloring of (a). The colored circles within the plot represent the distance of each amino acid to C3d, as indicated in the legend. The black circle represents the parent complex. A horizontal shaded box indicates mutations with a free energy value of ±50 kJ/mol of the parent

We applied a similar analysis to several other protein systems as well. Specifically, we recently examined the C3d–CR2 interaction.9,24 The results gave credibility to the recent controversy over the cocrystal structure of C3d–CR2.20 With the incorporation of recently published experimental data, the correlation between calculated and experimental free energies is poor, despite excessive charge playing a role in complex formation. Our results are consistent with the possibility that the published structure is not physiological, but rather an artifact of crystallographic conditions. Similarly, calculations with a docking model structure of Epstein-Barr virus glycoprotein 350–CR2 (gp350–CR2) yielded a similar finding (unpublished results). Relatively poor correlations between calculated and experimental free energy values brought the integrity of the model into question, especially considering the model was constructed using experimental data as constraints. The C3d–CR2 and gp350–CR2 show the efficacy of AESOP through negative results.

Clustering of Homologous Proteins and Domains

The AESOP analysis of homologous proteins poses different challenges due to an increase in the electrostatic diversity among protein analogs, when compared to alanine scan mutants. Substantial differences in amino acid composition (sequence identity), local structure, and charge distribution are possible within homologous families, despite having quite similar functions. One such system to which the AESOP framework has been applied is a family of Arabidopsis lipid transfer proteins (LTPs).7 In this study, electrostatic clustering was used to elucidate the unique functionality of one specific analog, Arab_LTP5. The unique character of Arab_LTP5 was believed to be due to its excessive positive charge (+14e), and the effects of this excessive charge could be manifested in Arab_LTP5’s amino acid sequence, charge distribution, or spatial distribution of electrostatic potential. Figure 4 provides examples of three different types of clustering in which LTP/LTP-like proteins were compared on the basis of (a) sequence similarity, (b) three-dimensional charge distribution, and (c) electrostatic similarity (Shell–DP method). These dendrograms show that neither sequence similarity nor charge distribution is sufficient for comparing this homologous family of proteins. Of these three types of comparisons, only the comparison of spatial distributions of electrostatic potential was able to illustrate the unique character of Arab_LTP5.7

FIGURE 4.

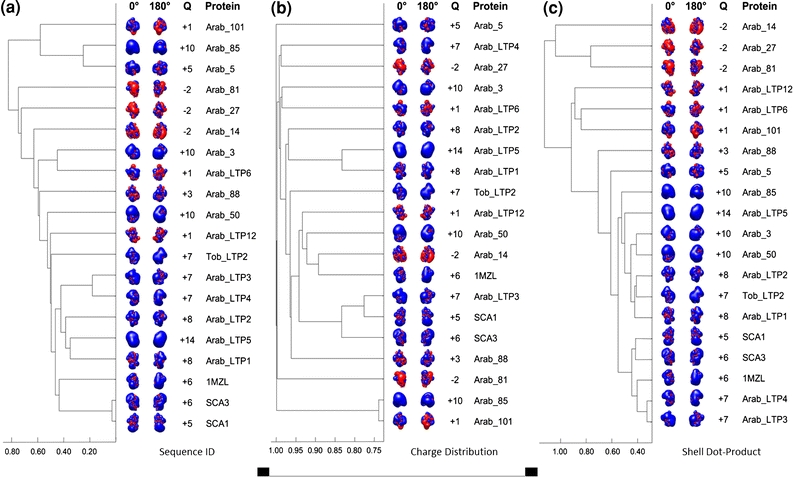
Dendrograms for the clustering of 20 LTP/LTP-like proteins based on (a) sequence identity; (b) charge distribution; and (c) ESD Shell–DP. Electrostatic potentials were calculated using ionic strengths corresponding to 50 mM ion concentration and ε_P = 2. Isopotential contours at two axial rotations are included for each LTP/LTP-like protein. The color code for the isopotential contours is blue for positive and red for negative electrostatic potential. Isopotential contours are plotted at ±1 k _B T/e

We have also applied the AESOP methods to another type of homologous protein family, the homologous CCP domains of complement regulator factor H.23 In this study, homology modeling and electrostatic calculations were used to analyze the electrostatic diversity of the CCP domains of factor H, with the goal of further developing our model for the role of electrostatics in complement regulation. Figure 5 illustrates the clustering results for electrostatic comparison of the 20 CCP modules of factor H based on the WB–LD clustering method. The dendrogram of Fig. 5 was generated using homology models for 9 CCP domains, while the remaining 11 structures originated from a combination of NMR and X-ray crystallographic structures obtained from the PDB. The use of the AESOP clustering methods allowed for the prediction of factor H contacts, including specific interactions with C3b macroglobulin (MG) domains and nonspecific interactions with polyanion-rich surfaces, which are important for factor I-mediated degradation of C3b.23 Electrostatic clustering analysis also provided insight into the pathobiology of involvement of specific factor H modules in disease.

FIGURE 5.

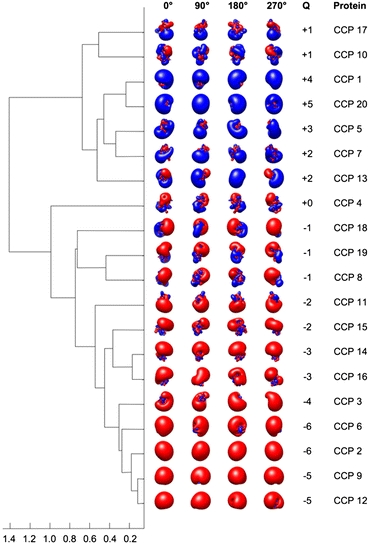
Dendrogram for the electrostatic clustering of the 20 CCP modules of factor H based on WB–LD. NMR or X-ray crystallographic structures were used for 11 CCP domains and homology models were used for 9 CCP domains. Electrostatic potentials were calculated using ionic strengths corresponding to 0 mM ion concentration and ε_P = 2. Isopotential contours at four axial rotations are included for each CCP module. The color code for the isopotential contours is blue for positive and red for negative electrostatic potential. Isopotential contours are plotted at ±1 k _B T/e

Ionization Free Energy and pH Dependence

We have applied electrostatic methods for determining pH and ionic strength dependence for protein properties, such as net charge (titration curves), stability (folding–unfolding transition), and association.32 We have studied the pH and ionic strength dependence of charge and stability of C3d and CR2 and of the C3d–CR2 complex, an important protein complex that acts as a link between innate and adaptive immunities.30,32,51 Calculations were based on a thermodynamic cycle for pH-dependent association, in which association free energy is decomposed into a process that incorporates the ionization properties of amino acids and a process with neutral amino acids.32,51 The results showed good agreement between calculated ionization free energies of association and experimental pH- and ionic strength-dependent association kinetics, and provided a decomposition of electrostatic and nonpolar contributions to association free energies.51 An earlier study30 had postulated the effects of long-range electrostatics in C3d–CR2 association using crystallographic structures. The study by Zhang et al. 51 used MD simulations to assess the significance of electrostatic potential fluctuations and CR2 modular motions in binding, and provided the detailed matrix of short/medium-range intra- and inter-molecular interaction energies. In addition, that study51 showed that ionization free energies of association for a series of C3d and CR2 mutants were predictive of relative experimental binding abilities. A subsequent study9 showed good correlations between calculated ionization free energies of association and electrostatic free energies of association at physiological pH. The difference between the two free energy calculations was that the former includes the pH dependence of ionization and takes into account the apparent pK_a values of amino acids, whereas the latter used the presumed ionization states of ionizable amino acids at physiological pH. The presumed ionization states are charged aspartic and glutamic acids, lysines and arginines, and charged termini, whereas histidines, tyrosines, and nondisulfide-bonded cysteines are neutral, unless selected to be charged based on apparent pK_a pre-calculation. It is well known that the pK_a values of ionizable amino acids within the protein can be shifted significantly compared to those of free amino acids in solution. The magnitude and direction (positive or negative) of the shifts depends on the local electrostatic (Coulombic and solvation) microenvironment. These types of shifts are particularly important for amino acids involved in binding and catalysis. Many reviews on ionization properties of proteins and the calculation of apparent pK_a values have been published, including one of ours with examples from systems we have with worked in the past,49 and we will not elaborate further here.

We have studied the pH and ionic strength dependence of stability of the 10th type III domain of human fibronectin (FNfn10).27 This type of calculation is possible by using a thermodynamic cycle that models the pH dependence of the folding–unfolding transition in a charged and neutral state, by taking into account the pH dependence of amino acid ionization when calculating charges.27,32,49,51 In agreement with experimental data, the calculations showed that at high ionic strength, FNfn10 is more stable at low pH compared to neutral pH.27 This was attributed to unfavorable interactions in a triplet of acidic residues that become weaker at high ionic strength, as Coulombic interactions are screened by solvent ions, or at low pH, as acidic amino acids become neutralized. Upon mutation of the central acidic residue, the calculations showed increased stability in agreement with experimental data.27 This study demonstrates the utility of electrostatics-based computational predictions for the design of proteins with tailored stabilities. In the case of FNfn10, higher stability provides a better scaffold for the attachment of novel antibody mimics (termed monobodies). The same study served as a medium to compare the effect of backbone and side chain flexibility on calculated pH- and ionic strength-dependent stabilities and to assess the accuracy and precision of calculated apparent pK_a values. This was accomplished by using an NMR ensemble of structures for the calculations and NMR-derived pK_a values of acidic amino acids for comparison with experimental data.27 We have also examined the titration curves and pH dependence of stability of two homologous plant proteins, SCA1 and SCA2, and discussed the findings in view of experimental data and functional models.8

In summary, calculated titration curves provide pH dependencies of charges and protein isoelectric points. Calculated stability curves provide the pH range of protein functionality. Calculated stability curves for protein complexes provide the pH dependencies of ionization free energies of association. The calculated pH-dependent processes discussed here take into account the ionization states of amino acids, which depend on favorable and unfavorable Coulombic interactions and favorable solvation or unfavorable desolvation effects. PB-based calculations of ionization properties are an excellent predictive medium of the effect of mutations in protein function, especially when the processes of binding and catalysis are involved, and in protein design when pH and ionic strength dependencies are of importance.

Electrostatic Design of Peptide-Based Inhibitors

PB electrostatic calculations are a useful tool in peptidic and peptidomimetic inhibitor design, in cases where design is based on peptides derived from native protein sequences. This is possible when the native proteins are excessively charged and binding to receptors is driven by electrostatic complementarity. The interaction of HIV-1 gp120 with the human receptor CCR5 takes place through a positively charged variable loop (V3 loop) in gp120 and a negatively charged N-terminal domain in CCR5. This electrostatic mechanism contributes in mediating viral entry and modulating biological activity in the human host cell. The V3 loop has variable positive net charges, depending on HIV-1 strains, thus it is of interest to examine the effect of charge on the inhibition of gp120–CCR5 interaction. We have shown using a series of V3 loop-derived peptides that there is an excellent correlation between calculated electrostatic potentials and experimental binding and inhibition data.31 We studied a series of peptides with variable excess of positive net charge in the range of +1 to +9, and found that as the positive electrostatic potential increased, the peptide binding and inhibition ability increased. Interestingly, a peptide with scrambled positive charges showed similar binding affinity and inhibitory activity as the parent peptide from which it was derived.31 The parent peptide had sequence from a viral strain and net charge +5, whereas the modified peptide had similar sequence, but with scrambled positions for lysine and arginine residues to a total net charge of also +5. In both cases, parent-viral and modified peptides, the patterns of spatial distributions of electrostatic potentials were similar. Given the notorious flexibility and mobility of the V3 loop, which is evidenced by the lack of observation of usable electron densities in crystal structures of free gp120, and our findings, we suggested that a possible avenue for anti-HIV drug design may not be based on structure but on the electrostatic properties of the V3 loop sequence. This approach may be an efficient way to design a drug which will account for the ability of HIV to mutate, by simultaneously targeting the numerous strains with variable sequences and flexible structures, but with positive charges at the V3 loop.

Perspectives

In this review, we discussed a number of tools for the analysis of electrostatics in proteins and protein complexes. The newly developed AESOP computational framework provides an integrative approach for elucidating the role of specific charged residues important for protein interaction and function. We have illustrated how different applications of AESOP have both improved calculation of electrostatic effects in proteins and shown the efficacy of computational methods to elucidate implications of electrostatics in binding and biological function. This computational framework can be used to analyze electrostatic data for mechanistic studies to understand basic biological function. It can also be used to guide experimental studies by providing a basis for the design of protein mutants and homologs with optimized functions. Such studies form a foundation for the design of protein therapeutics and biotechnology products.