Deformation of biological cells in the acoustic field of an oscillating bubble

Abstract

In this work we develop a theoretical framework of the interaction of microbubbles with bacteria in the ultrasound field using a shell model of the bacteria, following an approach developed previously [P. V. Zinin et al., Phys. Rev. E 72, 61907 (2005)]. Within the shell model, the motion of the cell in an ultrasonic field is determined by the motion of three components: the internal viscous fluid, a thin elastic shell, and the surrounding viscous fluid. Several conclusions can be drawn from the modeling of sound interaction with a biological cell: (a) the characteristics of a cell’s oscillations in an ultrasonic field are determined both by the elastic properties of the shell the viscosities of all components of the system, (b) for dipole quadrupole oscillations the cell’s shell deforms due to a change in the shell area this oscillation depends on the surface area modulus K_A, (c) the relative change in the area has a maximum at frequency $f_K\sim \frac{1}{2\pi }\sqrt{K_A/(\rho a^3)}$, where a is the cell’s radius and ρ is its density. It was predicted that deformation of the cell wall at the frequency f_K is high enough to rupture small bacteria such as E. coli in which the quality factor of natural vibrations is less than 1 (Q < 1). For bacteria with high value quality factors (Q > 1), the area deformation has a strong peak near a resonance frequency f_K; however, the value of the deformation near the resonance frequency is not high enough to produce sufficient mechanical effect. The theoretical framework developed in this work can be extended for describing the deformation of a biological cell under any arbitrary, external periodic force including radiation forces unduced by acoustical (acoustical levitation) or optical waves (optical tweezers).

I. INTRODUCTION

The frequencies of the normal modes of vibration for a spherical virus particle were estimated by Ford in 2003 [1]. Subsequent theoretical studies [2–4] led to the successful detection of the normal oscillations for low-frequency vibrational modes of bacteriophage M13 in water by Raman spectroscopy [5]. It was also demonstrated that by using a visible femtosecond laser, it is feasible to inactivate viruses such as the bacteriophage M13 through impulsive stimulated Raman scattering [6].

Normal vibrations of bacteria have also been considered recently [7]. Theoretical calculations indicate that high-quality resonances are possible for several types of bacteria that have radii greater than 5 µm. The calculations also show that it is more likely that Gram positive bacteria would have resonances than Gram negative bacteria because the cell wall (shell) of the Gram positive bacteria is much stiffer than that of Gram negative bacteria [7]. The frequency of the natural oscillations of bacteria are in the MHz frequency range and therefore such oscillations cannot be detected by Raman or Brillouin scattering [8]. Despite the fact that the quality factor for specific types of bacteria are relatively high, these resonances have not been readily observed in biological cell experiments [7]. Resonance oscillations of the cells were observed by Miller who imaged standing wave (high-quality resonance oscillation) in the cell wall of algae in a 1 MHz ultrasonic wave [9]. An explanation of why mechanical resonances of cells are difficult to excite by a plane acoustic wave was provided by Ackerman [10,11]. For drops, this problem was addressed by Marston and Apfel [12,13]. They found that the sound scattering cross section of the cells and drops at the frequency of the shape resonance was fairly small. For instance, for a D. carota cell the wavelength, λ, of the sound wave in water at the resonance frequency was estimated to be 1.67 mm [7]. This is 55 times greater than the radius of the D. carota cell: 30 µm. Since the cross section of the sound scattering by a small particle such as a bacterium is proportional to the fourth power of the ratio (a/λ)⁴, the effect of the sound wave on the bacteria at the frequency of the shape resonance is negligible. Marston and Apfel proposed to use modulated acoustic radiation pressure for efficient excitation of the quadrupole resonance of drops [13]. In their experiments, the acoustic radiation force in the field of standing ultrasonic wave was modulated in a such way that the wavelength of the carrier wave was close to the radius of the drop and the frequency of modulation was close to the frequency of the quadrupole surface resonance of the drop. Ackerman predicted that mechanical resonances of cells could be excited in the presence of microbubbles [14]. His idea was to excite shape vibrations of the red blood cell by an external force that (a) acts with frequency close to the resonance frequency of the cell and (b) that is uniform at the length comparable with the size of the cell [14]. A small stable bubble oscillating near a cell (at the resonance frequency of cell) may be a source of such excitation. The field generated by such a microbubble in acoustic wave decays with the distance from the bubble. The aim of this work is twofold: (a) to investigate possible biological effects in bacteria produced by microbubbles oscillating in the vicinity of a bacterium in the ultrasonic field and (b) to investigate the possibility of excitation of the resonance vibration in a bacterium by vibration microbubble. To achieve these goals, we develop a theoretical model of the interaction of microbubbles with bacteria in the ultrasound field. The model can be used for (a) studying effects of the mechanical resonances of bacteria (tension and deformation in the bacteria shell) in the vicinity of bubbles or ultrasound contrast agents in the surrounding liquid, (b) investigating the possibility of cell disruption at resonance frequency, and (c) understanding the effect of resonances on sonoporation in the ultrasound field relating the area deformation in the ultrasound field and enlarged diameter of pores in the cell’s shells (membranes).

II. MODEL

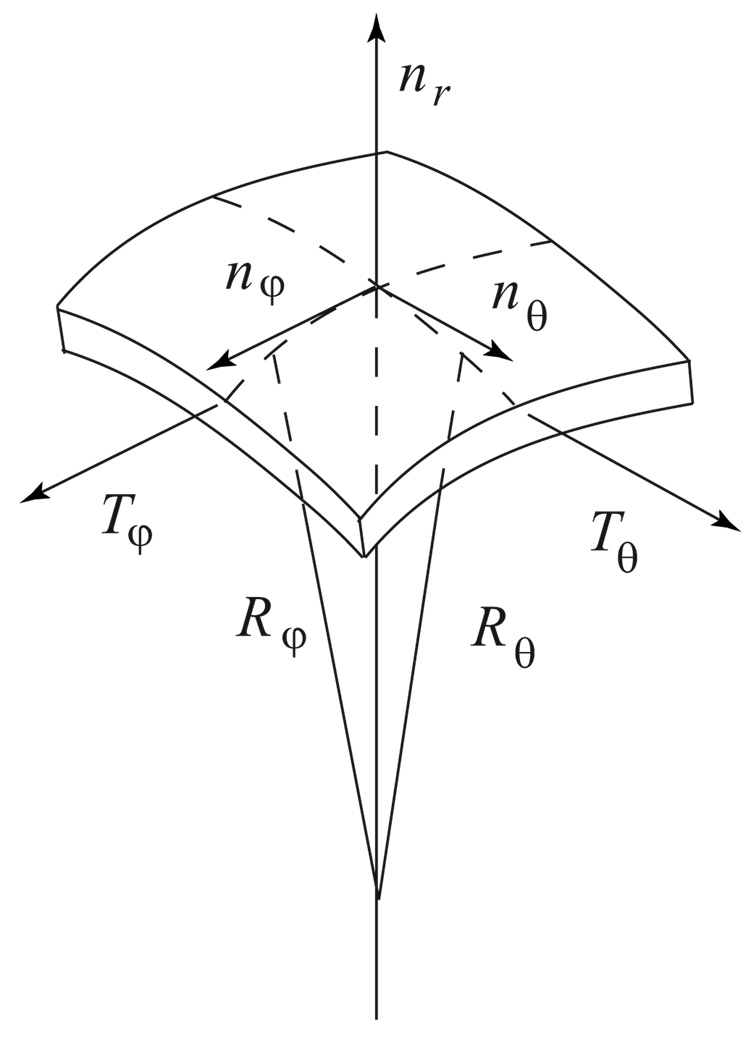
Modeling of the sound interaction with biological cells includes four theoretical approaches: (a) theory of sound scattering by liquid viscous drops [15,16], (b) theory of natural oscillations of viscous drops [17], (c) theory of shells and plates [18,19], and (d) theory of elasticity of biological membranes [20,21]. To describe the viscoelastic response of the cell to the sound field generated by a vibrating microbubble we will use the “shell model” of a cell (Fig. 1) described in detail elsewhere [7,22]. The shell model of the cell was successfully applied to analyze mechanisms of sound attenuation in blood and in erythrocyte suspensions [22]. A similar model was used for description of shape oscillations of drops in the presence of surfactants [23,24] and for modeling the recovery of nonadherent cells after micropipette extension [25]. Within the shell model, a bacterium is assumed to have a spherical shape of radius a (Fig. 2). A spherical shape of the cell is assumed for two reasons. First, it is possible to obtain an analytical solution for spherical objects [26]. Second, many bacteria indeed have a spherical shape (cocci). The cellular shell does not have uniform thickness [21], it is a stratified system which is composed of at least three layers differing in mechanical properties: bilipid membrane, external shell, and internal polymer network. Each layer makes a unique contribution to the resistance of the shell undergoing different types of deformation. However, for the cells considered in this study, the thickness of the shell h is much less than the characteristic size of the cell a: h ≪ a. For thin shells the equations of motion include the total values of the internal forces distributed over the thickness of the shell [19]. Within such an approximation the flexural moments and the intersecting stresses in the membrane may be neglected [19]. Within the shell model, the motion of the cell is composed of three components: the motions of the internal fluid, and the surrounding fluid, and the deformation of cell shell [22].

FIG. 1.

Stresses on the element of the spherical shell in the spherical coordinates (r, θ, φ).

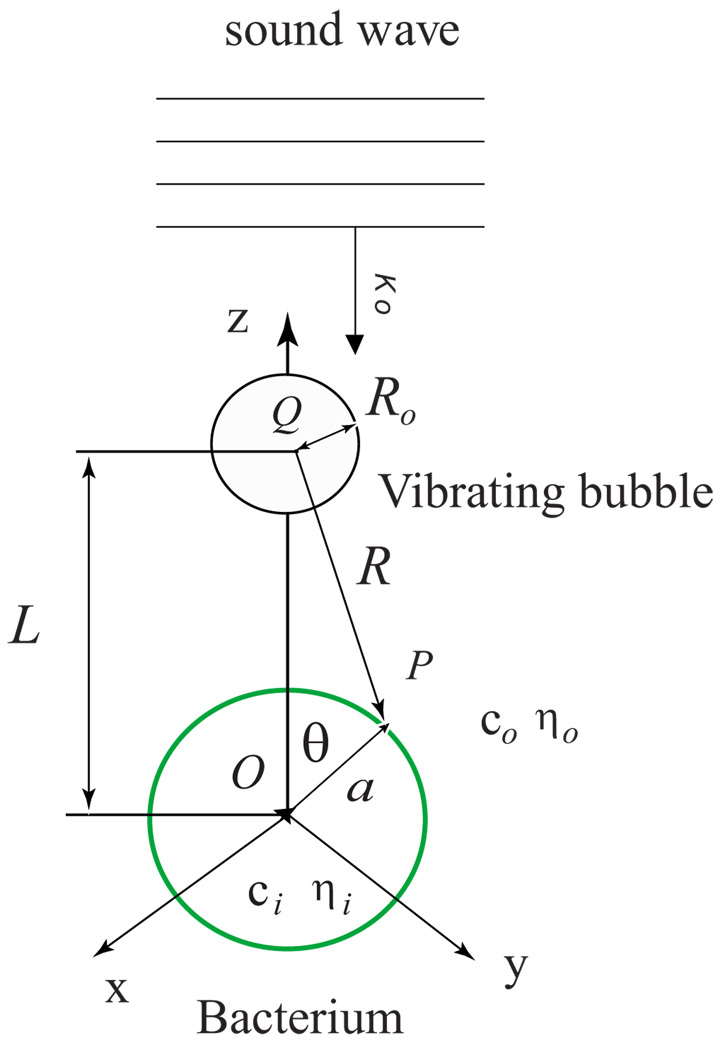
FIG. 2.

(Color online) Diagram of the interaction of a vibrating bubble with bacteria in ultrasound field. Following notations were introduced in the text and shown in the figure: xyz are Cartesian coordinates; θ is the zenith angle in the spherical coordinate system; a is the radius of the cell; R_o is the equilibrium radius of the bubble; L is the distance between center of the cell (O) and center of the bubble (Q); P is a point on the cell surface; R is the distance between center of the bubble and point P; k_o is the wave vector of the incident plane sound wave; c and η are sound velocity and viscosity of the corresponding liquids.

A. Wave equations

The fluid within and outside the cell is characterized by a density ρ, a velocity of sound c, a compressional or bulk viscosity ς, and a shear viscosity η. The values corresponding to the internal fluid will be designated by the subscript i and the values associated with the external fluid by o. The motion of the fluids is described by the particle velocity fields V_i and V_o and the pressures p_i and p_o, which are determined by a standard system of equations consisting of the equation of continuity, the Navier-Stokes equation and the linearized equation of state [27]. Following linear acoustic assumptions, we assume that perturbation of the fluid density ρ′ and pressure p′ caused by cell vibrations are small in comparison with static values of the density ρ and pressure p: p_total = p+p′; ρ_total=ρ+ρ′; p′ ≪ p; ρ′ ≪ ρ. In this approach, the equation of continuity can be written as [15]

$$\frac{\partial \rho \prime }{\partial t}+\rho \text{div}(\overrightarrow{V})=0,$$ (1)

the Navier-Stokes equation as

$$\rho \frac{\partial \overrightarrow{V}}{\partial t}=-\text{grad}(p\prime )+\eta \mathrm{\Delta }\overrightarrow{V}+(\varsigma +\eta /3)\text{grad div}(\overrightarrow{V}),$$ (2)

where Δ is the Laplacian, t is the time and the linearized equation of state is

$$p\prime =c^2\rho \prime .$$ (3)

The velocity field in the fluid may be represented as a superposition of two parts: potential part described by a scalar field Φ, and vortical part described by a vector field A⃗ [15,16,27]

$$\overrightarrow{V}=-\text{grad}\mathrm{\Phi }+\text{rot}\overrightarrow{A}.$$ (4)

Solutions for the potentials Φⁱ and Φ^o are sought in the form of the diverging and standing spherical waves and for A⃗ⁱ and A⃗^o in the form of viscous shear waves, which exponentially attenuate on both sides of the shell due to viscous dissipation. Substituting Eq. (4) into Eqs. (1)–(3), the wave equations can be expressed as

$$(\mathrm{\Delta }+k^2)\mathrm{\Phi }=0,$$ (5)

$$(\mathrm{\Delta }+{\chi }^2)\overrightarrow{A}=0,$$ (6)

where k = ω/c, $\chi =\sqrt{(i\omega \rho )/\eta }$, and ω is the angular frequency.

We introduce a system of spherical coordinates r, θ and φ; with the origin at the center of the shell (Fig. 1). The analysis of a shell of an arbitrary shape poses considerable mathematical difficulties; therefore, we limit the work in this initial study to the vibrations of a spherical shell. The V_r and V_θ components of the vector velocity V⃗ can be written in the spherical coordinate system as

$$V_r=-\frac{\partial \mathrm{\Phi }}{\partial r}+\frac{1}{r}{\mathrm{\Delta }}_{\theta }A,$$ (7)

$$V_{\theta }=-\frac{1}{r}\frac{\partial \mathrm{\Phi }}{\partial \theta }-\frac{1}{r}\frac{\partial (\mathit{\text{rA}})}{\partial r},$$ (8)

where

$${\mathrm{\Delta }}_{\theta }A=\frac{1}{\text{sin}\theta }\frac{\partial }{\partial \theta }(\text{sin}\theta A).$$ (9)

B. Boundary value problem

In the thin shell approximation, the cell wall is considered as an infinitely thin elastic layer. The boundary conditions evaluated at r = a include the kinematic conditions, the continuity of the velocities and the total stress balance [17,22,24]. It is assumed that both surfaces of the shell move at the same velocity, which is the velocity of the shell itself:

$${\overrightarrow{V}}^i{|}_{r=a}={\overrightarrow{V}}^o{|}_{r=a}=\frac{\partial \overrightarrow{W}}{\partial t}$$ (10)

or

$$V_r^o=V_r^i,V_{\theta }^o=V_{\theta }^i,$$ (11)

where W is the shell displacement. The radii of curvature of the cell’s shell are much larger than the thickness of the membrane structure (h / a ≪ 1). Due to the small thickness of the shell, the equation of motion of the shell can be replaced by the equilibrium equations (Fig. 1). The equations of mechanical equilibrium for an element for this spherical shell may be expressed in the following form [19]:

$${\sigma }_{\mathit{\text{rr}}}^o-{\sigma }_{\mathit{\text{rr}}}^i-\left(\frac{T_{\theta }}{R_{\theta }}+\frac{T_{\phi }}{R_{\phi }}\right)=0,$$ (12)

$${\sigma }_{\theta r}^o-{\sigma }_{\theta r}^i+\frac{1}{a}\left[\frac{\partial T_{\theta }}{\partial \theta }+\text{cot}\theta (T_{\theta }-T_{\phi })\right]=0,$$ (13)

where T_θ, T_ϕ are the normal tensions in the shell and R_θ, R_φ are the local radii of curvature. The components of the tensor of viscous stress acting on the shell on part of the fluid ${\sigma }_{\mathit{\text{rr}}}^o,{\sigma }_{\mathit{\text{rr}}}^i,{\sigma }_{\theta r}^o,{\sigma }_{\theta r}^i$ have the following forms [15]:

$${\sigma }_{rr}={\left[-p\prime +2\eta \frac{\partial V_r}{\partial r}+\left(\varsigma -\frac{2}{3}\eta \right)\text{div}\overrightarrow{V}\right]}_{r=a},$$ (14)

$${\sigma }_{\theta r}=\eta {\left[\frac{1}{a}\frac{\partial V_r}{\partial \theta }+\frac{\partial V_{\theta }}{\partial r}-\frac{V_{\theta }}{a}\right]}_{r=a}.$$ (15)

Equations (12) and (13) must be supplemented by relationships between the deformations and the internal forces in the shell. The equations of motion are written in an instantaneous, local system of coordinates associated with the perturbed surface; therefore, its radii of curvature R depends on the relative movement of the shell W (V = ∂W/∂t). Primarily two forces resist deformation of the shell of the cell: constant tension T_o and the force of surface elasticity. The resistance to the change in the surface area is characterized by the area compression modulus K_A and the resistance to the shear deformation by modulus μ [20,21]. The relationship between the tensions T_θ, T_φ and the strains e_θθ and e_φφ for a thin spherical shell have the following form [21,28]:

$$T_{\theta }=K_A(e_{\theta \theta }+e_{\phi \phi })+\mu (e_{\theta \theta }-e_{\phi \phi })+T_o,$$ (16)

$$T_{\phi }=K_A(e_{\theta \theta }+e_{\phi \phi })-\mu (e_{\theta \theta }-e_{\phi \phi })+T_o.$$ (17)

Here (e_θθ+e_φφ) = e_S is the relative change in the area of the element of the surface. For bacteria, the moduli μ and K_A are similar in magnitude [20,29]. For cells without walls, the surface shear modulus is smaller than K_A: μ ≪ K_A, by many orders [21]. The strains are expressed in terms of the displacement W_r and W_θ:

$$e_{\theta \theta }=\frac{1}{a}\left(W_r+\frac{\partial W_{\theta }}{\partial \theta }\right),$$ (18)

$$e_{\phi \phi }=\frac{1}{a}(W_r+W_{\theta }\text{cot}\theta ).$$ (19)

The radii of curvature of a perturbed spherical shell are expressed as

$$\frac{1}{R_{\theta }}=\frac{1}{a}\left(1-\frac{W_r}{a}-\frac{1}{a}\frac{{\partial }^2{W}_r}{\partial {\theta }^2}\right),$$ (20)

$$\frac{1}{R_{\varphi }}=\frac{1}{a}\left(1-\frac{W_r}{a}-\frac{1}{a}\text{cot}\theta \frac{\partial W_r}{\partial \theta }\right).$$ (21)

Using Eqs. (14)–(21), we can write the equations of motion of the shell in the following form:

$${\sigma }_{\mathit{\text{rr}}}^o-{\sigma }_{\mathit{\text{rr}}}^i+\frac{T_o}{a^2}\left(2W_r+{\mathrm{\Delta }}_{\theta }\frac{\partial W_r}{\partial \theta }\right)-\frac{2K_A}{a^2}(2W_r+{\mathrm{\Delta }}_{\theta }{W}_{\theta })=0,$$ (22)

$${\sigma }_{\theta r}^o-{\sigma }_{\theta r}^i+\frac{K_A}{a^2}\frac{\partial }{\partial \theta }(2W_r+{\mathrm{\Delta }}_{\theta }{W}_{\theta })+\frac{\mu }{a^2}\left(2W_{\theta }+\frac{\partial }{\partial \theta }{\mathrm{\Delta }}_{\theta }{W}_{\theta }\right)=0,$$ (23)

where

$${\mathrm{\Delta }}_{\theta }W=\frac{1}{\text{sin}\theta }\frac{\partial }{\partial \theta }(\text{sin}\theta W).$$

The above equations determine the dynamic conditions between the motion of the shell and that of interior and surrounding fluids.

C. Scattering of the sound waves by a cell

To find the acoustic field scattered by the bacteria, we represent the incident wave as a solution of the wave equation in spherical coordinates with its origin at the particle center. For simplicity, we consider only oscillations possessing axial symmetry. For the case of axial symmetry, equations (5) and (6) are solved in terms of series expansions of spherical wave functions. The acoustic field outside of the cell is a superposition of the incident field and the scattered field [15]

$${\mathrm{\Phi }}^o={\mathrm{\Phi }}^{\text{inc}}+{\mathrm{\Phi }}^s,$$ (24)

where the incident wave can be represented as a spherical wave decomposition

$${\mathrm{\Phi }}^{\text{inc}}={\displaystyle \sum _{n=0}^{\infty }{E}_n{j}_n(k_{o}r)P_n(\text{cos}\theta )e^{-i\omega t}},$$ (25)

where P_n(cos θ) are the Legendre polynomials [30] and j_n(kr) are the spherical Bessel functions [30]. In this study, we only consider the excitation of the cell vibration by acoustic field. However, vibrations of cell can also be effectively excited by other means such as acoustic radiation force [13,31] or an optical radiation force in the focus of the laser beam [32]. Coefficient E_n is determined from the equation for spherical wave decomposition of the incident wave. For a plane sound wave the coefficient E_n has the form [33]

$$E_n=\frac{1}{\omega }\sqrt{\frac{2I{c}_o}{{\rho }_o}}{i}^n(2n+1),$$

where I is the sound intensity. The expression for E_n in the modulated acoustical filed can be found elsewhere [12,13]. The response of the cell to an external force is determined by a set of four undetermined coefficients A_n, B_n, C_n, D_n. We may write these for the surrounding fluid as follows [15,16]:

$${\mathrm{\Phi }}^s(r,\theta )={\displaystyle {\sum }_{n=0}^{\infty }{A}_n{h}_n(k_{o}r)P_n(\text{cos}\theta )e^{-i\omega t}},$$ (26)

$$\begin{array}{ll}{A}^o(r,\theta )& ={\displaystyle {\sum }_{n=0}^{\infty }{C}_n{h}_n({\chi }_{o}r)P_n^1(\text{cos}\theta )e^{-i\omega t}}\hfill \\ & =-{\displaystyle {\sum }_{n=1}^{\infty }{C}_n{h}_n({\chi }_{o}r)}\frac{\partial P_n(\text{cos}\theta )}{\partial \theta }{e}^{-i\omega t},\hfill \end{array}$$ (27)

and for internal liquid

$${\mathrm{\Phi }}^i(r,\theta )={\displaystyle {\sum }_{n=0}^{\infty }{B}_n{j}_n(k_{i}r)P_n(\text{cos}\theta )e^{-i\omega t}},$$ (28)

$$\begin{array}{ll}{A}^i(r,\theta )& ={\displaystyle {\sum }_{n=0}^{\infty }{D}_n{h}_n({\chi }_{i}r)P_n^1(\text{cos}\theta )e^{-i\omega t}}\hfill \\ & =-{\displaystyle {\sum }_{n=1}^{\infty }{D}_n{j}_n({\chi }_{i}r)}\frac{\partial P_n(\text{cos}\theta )}{\partial \theta }{e}^{-i\omega t},\hfill \end{array}$$ (29)

where h_n(kr) are the spherical Hankel function of the first kind [30] and A is the φ component of vector potential $\overrightarrow{A}:\overrightarrow{A}=A{\overrightarrow{i}}_{\varphi }.$

According to Eqs. (25)–(29), the movement of the cells in an ultrasonic field is described by the superposition of oscillations with different angular symmetry P_n(cos θ). For each value of n, the unknown amplitudes are linked by four linear algebraic equations arising from the boundary conditions (10), (11), (22), and (23).

With this linear approach, it is possible to consider the response of the cell to ultrasound at each mode of oscillation n. At the zeroth harmonic, the contribution of the shell to the scattering is insignificant [K_A/(ρac) ≪ 1]. Therefore, the spherical symmetrical scattering for biological cell is not very different from scattering for a simple drop (see Appendix A). The presence of the shell begins to be significant for dipole oscillations.

Substituting solutions for scalar and vector potentials into Eqs. (7) and (8) and using boundary conditions (10), (11), (22), and (23) we obtain a system of four equations for four undetermined coefficients A_n, B_n, C_n, D_n:

$$\begin{array}{l}-z_o{h}_n^{\prime }(z_o)A_n+z_i{j}_n^{\prime }(z_i)B_n+n(n+1)h_n({\xi }_o)C_n\\ \hfill -n(n+1)j_n({\xi }_i)D_n=z_o{j}_n^{\prime }(z_o)E_n,\hfill \end{array}$$ (30)

$$\begin{array}{l}-h_n(z_o)A_n+j_n(z_i)B_n+[{\xi }_o{h}_n^{\prime }({\xi }_o)+h_n({\xi }_o)]C_n\\ \hfill -[{\xi }_i{j}_n^{\prime }({\xi }_i)+j_n({\xi }_i)]D_n=j_n(z_o)E_n,\hfill \end{array}$$ (31)

$$\begin{array}{cc}\hfill \frac{{\rho }_o}{{\rho }_{*}}& h_n(z_o)A_n-\{\left[\frac{{\rho }_i}{{\rho }_{*}}+\frac{2{\omega }_{\mathit{\text{Kn}}}^2}{{\omega }^2}-n(n+1)\mathrm{\Delta }\xi \right]j_n(z_i)\hfill \\ & -\left[\frac{4{\omega }_{\mathit{\text{Kn}}}^2+{\omega }_{\mathit{\text{Tn}}}^2}{n(n+1){\omega }^2}-2\mathrm{\Delta }\xi \right]z_i{j}_n^{\prime }(z_i)\}{B}_n\hfill \\ & +\{\left[2\frac{{\omega }_{\mathit{\text{Kn}}}^2}{{\omega }^2}-n(n+1)\mathrm{\Delta }\xi \right]{\xi }_i{j}_n^{\prime }({\xi }_i)\hfill \\ & -\left[\frac{2{\omega }_{\mathit{\text{Kn}}}^2+{\omega }_{Tn}^2}{{\omega }^2}-n(n+1)\mathrm{\Delta }\xi \right]j_n({\xi }_i)\}{D}_n\hfill \\ & =-\frac{{\rho }_o}{{\rho }_{*}}{j}_n(z_o)E_n,\hfill \end{array}$$ (32)

$$\begin{array}{l}\left\{\left[\frac{{\omega }_{\mathit{\text{Kn}}}^2+{\omega }_{\mu n}^2}{{\omega }^2}-\mathrm{\Delta }\xi \right]j_n(z_i)-\left[\frac{2{\omega }_{\mathit{\text{Kn}}}^2}{n(n+1){\omega }^2}-\mathrm{\Delta }\xi \right]z_i{j}_n^{\prime }(z_i)\right\}{B}_n\\ -\frac{{\rho }_o}{{\rho }_{*}}{h}_n({\xi }_o)C_n+\{[\frac{{\omega }_{\mathit{\text{Kn}}}^2-{\omega }_{\mu n}^2}{{\omega }^2}+\frac{{\rho }_i}{{\rho }_{*}}-(n^2+n\hfill \\ -1)\mathrm{\Delta }\xi ]j_n({\xi }_i)-\left[\frac{{\omega }_{\mathit{\text{Kn}}}^2+{\omega }_{\mu n}^2}{{\omega }^2}-\mathrm{\Delta }\xi \right]{\xi }_i{j}_n^{\prime }({\xi }_i)\}{D}_n=0,\hfill \end{array}$$ (33)

where z_i=k_ia, z_o=k_oa, ξ_i = χ_ia, ξ_o = χ_oa. The mechanical response of the cell to the external stimulus depends on the relation between the frequency of sound ω and characteristic frequencies ω_μ, ω_T, ω_Rω_K:

$$\begin{array}{l}\hfill {\omega }_{\mathit{\text{Kn}}}^2=\frac{n(n+1)K_A}{{\rho }_{*}{a}^3},\hfill \\ \hfill {\omega }_{\mu n}^2=\frac{(n-1)(n+2)\mu }{{\rho }_{*}{a}^3},\hfill \\ \hfill {\omega }_{\mathit{\text{Tn}}}^2=\frac{(n-1)n(n+1)(n+2)T_o}{{\rho }_{*}{a}^3}\hfill \end{array}$$ (34)

characterizing the restoring forces in the shell and normalized liquid density

$${\rho }_{*}=(n+1)*{\rho }_i+n{\rho }_o.$$ (35)

The parameter

$$\mathrm{\Delta }\xi =\frac{2({\eta }_i-{\eta }_o)}{i\omega {\rho }_{*}{a}^2}=2\left[\frac{{\rho }_i}{{\rho }_{*}{\xi }_i^2}-\frac{{\rho }_o}{{\rho }_{*}{\xi }_o^2}\right]$$ (36)

expresses the process of mechanical relaxation due to the viscous forces in the fluid.

As indicated by Ackerman [34], the wavelength of the sound waves in water, λ at the frequency of mechanical resonances of cell is much longer than the radius of cell (long-wave approximation): a / λ ≪ 1. In the long-wave approximation (k_ia ≪ 1, k_oa ≪ 1) we can use the following relationship for spherical functions for n ≥ 1:

$$\begin{array}{l}\hfill (k_{i}a)j_n^{\prime }(k_{i}a)\approx n{j}_n(k_{i}a),\hfill \\ \hfill (k_{o}a)h_n^{\prime }(k_{o}a)\approx -(n+1)h_n(k_{o}a),\hfill \\ \hfill (k_{o}a)j_n^{\prime }(k_{o}a)\approx n{j}_n(k_{o}a).\hfill \end{array}$$ (37)

Then, the system (30)–(33) becomes (for n ≥ 1)

$$(n+1){\mathrm{\Phi }}_n^o+n{\mathrm{\Phi }}_n^i+n(n+1)A_n^o-n(n+1)A_n^i=n{j}_n(z_o)E_n,$$ (38)

$$\begin{array}{c}-{\mathrm{\Phi }}_n^o+{\mathrm{\Phi }}_n^i+\frac{1}{{\mathcal{H}}_n({\xi }_i)}[1-n{\mathcal{H}}_n({\xi }_i)]A_n^o\hfill \\ \hfill +\frac{1}{{\mathcal{J}}_n({\xi }_i)}[1-(n+1){\mathcal{J}}_n({\xi }_i)]A_n^i=j_n(z_o)E_n,\end{array}$$ (39)

$$\begin{array}{cc}\hfill {\gamma }_o& {\mathrm{\Phi }}_n^o-\left\{{\gamma }_i+\frac{2(n-1)}{(n+1)}{\tilde{\omega }}_{\mathit{\text{Kn}}}^2-\frac{1}{(n+1)}{\tilde{\omega }}_{\mathit{\text{Tn}}}^2-n(n-1)\mathrm{\Delta }\xi \right\}{\mathrm{\Phi }}_n^i\\ & -\frac{1}{{\mathcal{J}}_n({\xi }_i)}\{{\tilde{\omega }}_{\mathit{\text{Tn}}}^2{\mathcal{J}}_n({\xi }_i)+[2{\tilde{\omega }}_{\mathit{\text{Kn}}}^2-n(n+1)\mathrm{\Delta }\xi ]\hfill \\ & \times [1-(n-1){\mathcal{J}}_n({\xi }_i)]\}{A}_n^i=-{\gamma }_o{j}_n(z_o)E_n,\hfill \end{array}$$ (40)

$$\begin{array}{c}\left\{\frac{(n-1)}{(n+1)}{\tilde{\omega }}_{\mathit{\text{Kn}}}^2+{\tilde{\omega }}_{\mu n}^2+(n-1)\mathrm{\Delta }\xi \right\}{\mathrm{\Phi }}_n^i-{\gamma }_o{A}_n^o\\ +\frac{1}{{\mathcal{J}}_n({\xi }_i)}\{{\gamma }_i{\mathcal{J}}_n({\xi }_i)+{\tilde{\omega }}_{\mathit{\text{Kn}}}^2[1-(n-1){\mathcal{J}}_n({\xi }_i)]\hfill \\ +{\tilde{\omega }}_{\mu n}^2[1-(n+1){\mathcal{J}}_n({\xi }_i)]\hfill \\ -[1+(n^2-1){\mathcal{J}}_n({\xi }_i)]\mathrm{\Delta }\xi \}{A}_n^i=0,\hfill \end{array}$$ (41)

where we introduce the following notation:

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_n^o=A_n{h}_n(z_o),A_n^o=C_n{h}_n({\xi }_o),\hfill \\ \hfill {\mathrm{\Phi }}_n^i=B_n{j}_n(z_i),A_n^i=D_n{j}_n({\xi }_i),\hfill \end{array}$$ (42)

$${\mathcal{J}}_n({\xi }_i)=\frac{j_n({\xi }_o)}{j_{n+1}({\xi }_i){\xi }_i},$$ (43)

$${\mathcal{H}}_n({\xi }_o)=\frac{h_n({\xi }_o)}{h_{n-1}({\xi }_o){\xi }_o}$$ (44)

and nondimensional frequencies and densities

$${\tilde{\omega }}_{\mathit{\text{Kn}}}^2=\frac{{\omega }_{\mathit{\text{Kn}}}^2}{{\omega }^2},{\tilde{\omega }}_{\mu n}^2=\frac{{\omega }_{\mu n}^2}{{\omega }^2},{\tilde{\omega }}_{\mathit{\text{Tn}}}^2=\frac{{\omega }_{\mathit{\text{Tn}}}^2}{{\omega }^2},$$ (45)

$${\gamma }_o=\frac{{\rho }_o}{{\rho }_{*}},{\gamma }_i=\frac{{\rho }_i}{{\rho }_{*}}.$$ (46)

For n = 0, boundary conditions are written in Appendix A. To express deformation of the shell, we use the solution for ${\mathrm{\Phi }}_n^i$ and $A_n^i$ (n ≥ 0)

$$\begin{array}{ll}{\mathrm{\Phi }}_n^i=& (2n+1){\gamma }_o\frac{E_n{j}_n(z_o)}{d^n(\omega )}\{{\gamma }_i{\mathcal{J}}_n({\xi }_i)+{\gamma }_o{\mathcal{H}}_n-{\mathcal{H}}_n({\xi }_o){\mathcal{J}}_n({\xi }_i)[n{\gamma }_i+(n+1){\gamma }_o]+{\tilde{\omega }}_{\mathit{\text{Kn}}}^2[1-(n-1){\mathcal{J}}_n({\xi }_i)][1-(n+2){\mathcal{H}}_n({\xi }_o)]\hfill \\ & +{\tilde{\omega }}_{\mu n}^2[1-(n+1){\mathcal{J}}_n({\xi }_i)][1-n{\mathcal{H}}_n({\xi }_o)]-{\mathrm{\varpi }}_{\mathit{\text{Tn}}}^2{\mathcal{H}}_n({\xi }_o){\mathcal{J}}_n({\xi }_i)-[1+(n^2-1){\mathcal{J}}_n({\xi }_i)-n(n+2){\mathcal{H}}_n({\xi }_o)]\mathrm{\Delta }\xi \},\hfill \end{array}$$ (47)

$$\begin{array}{ll}{A}_n^i=& (2n+1){\gamma }_o\frac{E_n{j}_n(z_o)}{(n+1)}\frac{{\mathcal{J}}_n({\xi }_i)}{d^n(\omega )}\{(n+1)({\gamma }_i-{\gamma }_o){\mathcal{H}}_n({\xi }_o)-{\mathrm{\varpi }}_{\mathit{\text{Tn}}}^2{\mathcal{H}}_n({\xi }_o)-(n-1){\tilde{\omega }}_{Kn}^2[1-(n+2){\mathcal{H}}_n({\xi }_o)]\hfill \\ & -(n+1){\mathrm{\varpi }}_{\mu n}^2[1-n{\mathcal{H}}_n({\xi }_o)]-(n^2-1)\mathrm{\Delta }\xi \}.\hfill \end{array}$$ (48)

The expression for the determinant dⁿ(ω) was derived elsewhere [7]:

$$d^n(\omega )=d_D^n(\omega )+{\tilde{\omega }}_{\mathit{\text{Kn}}}^2{d}_C^n(\omega ),$$ (49)

where

$$d_D^n(\omega )=(1-{\tilde{\omega }}_{\mathit{\text{Tn}}}^2)[{\gamma }_o{\mathcal{H}}_n({\xi }_o)+{\gamma }_i{\mathcal{J}}_n({\xi }_i)-\mathrm{\Delta }\xi ]-[(2n+1){\gamma }_i{\mathcal{J}}_n({\xi }_i)-\mathrm{\Delta }\xi n(n+2)][(2n+1){\gamma }_o{\mathcal{H}}_n({\xi }_o)+\mathrm{\Delta }\xi (n^2-1)],$$ (50)

$$\begin{array}{ll}{d}_C^n(\omega )=& (1-{\tilde{\omega }}_{\mathit{\text{Tn}}}^2)(1+\beta )-4{\tilde{\omega }}_{\mu n}^2-{\gamma }_i{\mathcal{J}}_n({\xi }_i)[{(n-1)}^2+\beta {(n+1)}^2]-{\gamma }_o{\mathcal{H}}_n({\xi }_o)[{(n+2)}^2+\beta n(n+1)]\hfill \\ & -2\mathrm{\Delta }\xi [(n-1)(n+2)-\beta n(n+1)],\hfill \end{array}$$ (51)

where

$$\beta =\frac{{\omega }_{\mu n}^2}{{\omega }_{\mathit{\text{Kn}}}^2}.$$ (52)

Every partial term describing the nth mode of oscillations contains, except for the Legendre polynomials, the product of two terms; one of which (E_n) describes the structure of the incident ultrasonic field, and the other which determines the frequency dependence of the mechanical response of the cell to an external stimulus. The derivation of the analytical solutions for ${\mathrm{\Phi }}_n^i$, Eq. (47), and $A_n^i$, Eq. (48), is lengthy, and is omitted for brevity. However, ${\mathrm{\Phi }}_n^i$ and $A_n^i$ can be obtained by solving the system of linear equations (38)–(41) numerically.

D. Bubble cells interaction

We limit the investigation to bacteria interaction with stable microbubbles (“stable cavitation” [35]) oscillating in the ultrasonic field. Deformation of the cell wall in the plane wave is negligible for most biological cells. It is in part due to the fact that characteristic frequencies ω_μ, ω_T, ω_R, ω_K of biological cells are smaller that the frequency of the geometrical resonance ω_a = a / c. At frequencies lower than geometrical resonance, the scattering cross section is described by Rayleigh scattering and is proportional to the (a / λ)⁴. Therefore, the efficiency of the sound plane wave interaction with the cell is small if (a / λ) ≪ 1 and the effect of the sound wave on the bacteria at frequency of the shape resonance is negligible. That was a reason why Marston and Apfel suggested to use modulated ultrasound for studying quadrupole surface resonance behavior of drops [12,13]. For an effective interaction of ultrasound fields with a cell it is necessary to create a field with nonuniformity of the same order as a cell dimension. A powerful nonuniform ultrasound field can be created by a small-volume radiator radiating spherical waves in the close vicinity of the cell. Nyborg and his colleagues used an ultrasound needle in biological experiments to generate powerful spherical acoustic waves in the close vicinity of cells [36,37]. In biological media and liquids, the source of such spherical waves are cavitation bubbles, oscillating in the ultrasound field [14,38] so we consider deformation of the cell wall in the field of an oscillating bubble with negligible effect of the plane wave on the cell. The sound wave excites the radial oscillation of a bubble at a frequency close to the resonance oscillation of the bubble. If the bubble is located near the cell, then the spherical wave irradiated by the bubble is not uniform and may excite shape oscillations of the cell. A plane sound wave excites radial vibrations of the gas bubble and subsequently an acoustic field generated by the gas bubble is scattered by a cell which effects deformation of the cell’s membrane or wall.

Let P(a, θ, 0) be the point of observation and Q(L, 0, 0) be the source point of a spherical wave excited by a bubble (Fig. 2). The coordinates (a, θ, 0) and (L, 0, 0) refer to a fixed coordinate system whose origin is O. Let R be the distance between points Q and P. In the long wavelength limit k_oR_o ≪ 1, the acoustical field irradiated by a bubble has a simple analytical expression [27]

$${\mathrm{\Phi }}^{\text{inc}}=\frac{V_p{R}_o^2}{R}{e}^{i{k}_{o}R},$$ (53)

where V_p is the oscillation velocity of the surface of bubble. The distance R can be expressed with the distances L and a using the cosine theorem

$$R=\sqrt{L^2+a^2-2\mathit{\text{La}}\text{cos}\theta }.$$ (54)

Using addition theorem [33] (Chap. 7) we get for e^ik_oR/R

$$\frac{e^{i{k}_{o}R}}{R}=i{k}_o{\displaystyle \sum _{n=0}^{\infty }(2n+1)h_n(k_{o}L)j_n(k_{o}a)P_n(\text{cos}\theta ).}$$ (55)

Inserting Eq. (55) into Eq. (53) we obtain the field generated by a bubble

$${\mathrm{\Phi }}^{\text{inc}}=i{k}_o{V}_p{R}_o^2{\displaystyle \sum _{n=0}^{\infty }(2n+1)h_n(k_{o}L)j_n(k_{o}a)P_n(\text{cos}\theta ).}$$ (56)

An expression for the oscillation velocity of the surface of bubble V_p can be approximated from the following considerations. We represent displacement of the bubble surface, as in the monochromatic field, as R = Ro + ΔR_oe^−iωt, where R_o is the equilibrium radius of the bubble and ΔR_o is the amplitude of the bubble oscillation in the incident sound wave. Since V_p = ∂R/∂t, then V_p = −iωΔR_o. An expression for the incident field (59) has the following form:

$${\mathrm{\Phi }}^{\text{inc}}=\omega k_o{R}_o^3\frac{\mathrm{\Delta }{R}_o}{R_o}{\displaystyle \sum _{n=0}^{\infty }(2n+1)h_n(k_{o}L)j_n(k_{o}a)P_n(\text{cos}\theta ).}$$ (57)

The oscillation of a bubble in ultrasound fields has an nonlinear character, but at low sound intensity it may be linear and stable [39]. In this paper, we investigate the limiting case of stationary, linearly oscillating bubbles. The oscillation of such bubbles in ultrasound fields is given by the well-known linear resonance curves [39,38]:

$$\mathrm{\Delta }{R}_o=-\frac{p_m}{{\rho }_o{R}_o({\omega }^2-{\omega }_{\text{bub}}^2-i{\delta }_R{\omega }^2)},$$ (58)

where δ_R is a damping constant, p_m is the amplitude of pressure in incident plane wave, ω_bub is the resonance frequency of bubble. For the incident plane wave, we use $P_m=\sqrt{2I{c}_o{\rho }_o}$.

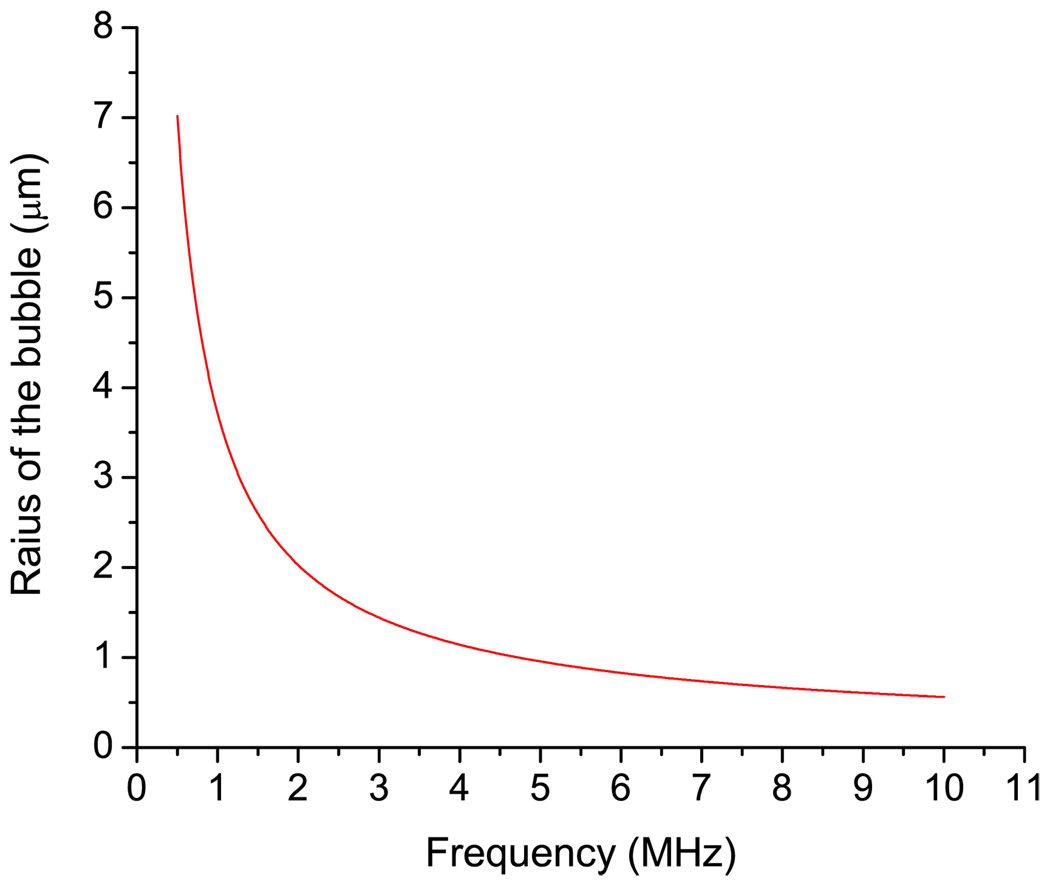
For the frequency range up to 10 MHz, the linear resonance radius of the bubble R_o can be determined from the Minnaert’s formula [39] corrected for surface tension σ_ST:

$$f_o=\frac{1}{2\pi R_o}\sqrt{\frac{3{\gamma }_b}{{\rho }_o}\left[P_o+\left(1-\frac{1}{3{\gamma }_b}\right)\frac{2{\sigma }_{\text{ST}}}{R_o}\right]},$$ (59)

where γ_b ∼ 1.4 is the ratio of specific heats (air) and P_o = 10⁵ Pa is the pressure in liquid under normal conditions. Calculations conducted using Eq. (62) of the resonance radius of the bubble as a function of frequency are shown in Fig. 3. The surface tension value (σ_ST = 0.0725 N/cm) is from Ref. [40]. For a range of frequencies from 20 KHz to several MHz, the damping of the resonance oscillation of bubble is only slightly dependent on the frequency, thus it is possible to approximate it as a constant. The ultrasound intensity determines the magnitude of the bubble displacement in the frequency range from 20 KHz to 10 MHz.

FIG. 3.

(Color online) Radius of a bubble at its linear resonance as a function of the frequency from Minnaert’s Eq. (67).

Using Eqs. ((57) and (58) we can determine the coefficient E_n for a spherical wave irradiated by an oscillating bubble

$$E_n=\omega \frac{\mathrm{\Delta }R}{R_o}{k}_o{R}_o^3(2n+1)h_n(k_{o}L).$$ (60)

The most significant interaction of the secondary radiation force of the bubble on the cells is the dilatation of the shell, because this kind of deformation may lead to cell disruption and the formation of pores in the cell membrane. Using expressions (48) and (49), an analytical expression can de derived for the local area deformation of the bacterium shell in the ultrasound field:

$$\frac{\mathrm{\Delta }S}{S}=e_{\theta \theta }+e_{\varphi \varphi }=\frac{1}{a}(2W_R+{\nabla }_{\theta }^2{W}_{\theta })=\frac{i}{a\omega }(2V_r+{\mathrm{\Delta }}_{\theta }{V}_{\theta }).$$ (61)

The expression for the 2V_r + Δ_θV_θ has a compact form

$$\begin{array}{ll}2V_r+{\mathrm{\Delta }}_{\theta }{V}_{\theta }=& -2\frac{\partial {\mathrm{\Phi }}_0^i(r)}{\partial r}{P}_0(\text{cos}\theta )+\frac{1}{a}{\displaystyle \sum _{n=1}^{\infty }n{P}_n(\text{cos}\theta )}\hfill \\ & \times \{(n-1){\mathrm{\Phi }}_n^i(r)+(n+1)A_n^i(r)\hfill \\ & \times \frac{1}{{\mathcal{J}}_n({\xi }_i)}[1-(n-1){\mathcal{J}}_n({\xi }_i)]\}.\hfill \end{array}$$

Thus, the analytical expression for the area deformation of the cell wall is

$$\frac{\mathrm{\Delta }S}{S}=\frac{i}{a^2\omega }{\displaystyle \sum _{n=1}^{\infty }{\gamma }_o{E}_n{j}_n(z_o)n(2n+1)\frac{d_S^n(\omega )}{d^n(\omega )}}{P}_n(\text{cos}\theta ),$$ (62)

where

$$\begin{array}{ll}{d}_S^n(\omega )=& \{[(n+1)({\gamma }_i-{\gamma }_o)+(n-1){\gamma }_o-{\mathrm{\varpi }}_{\mathit{\text{Tn}}}]{\mathcal{H}}_n({\xi }_o)\hfill \\ & +(n-1){\gamma }_i{\mathcal{J}}_n({\xi }_i)[1-(2n+1){\mathcal{H}}_n({\xi }_o)]\hfill \\ & -[2{\mathrm{\varpi }}_{\mu n}+\mathrm{\Delta }\xi (n-1)(n+2)][1-n{\mathcal{H}}_n({\xi }_o)]\}.\hfill \end{array}$$ (63)

Replacing E_n in Eq. (64) we have

$$\begin{array}{ll}\frac{\mathrm{\Delta }S}{S}=& i\frac{\mathrm{\Delta }R}{R_o}\frac{R_o^2}{a^2}(k_o{R}_o){\displaystyle \sum _{n=1}^{\infty }n{(2n+1)}^2{j}_n}(k_{o}a)\hfill \\ & \times h_n(k_{o}L){\gamma }_o\frac{d_S^n(\omega )}{d^n(\omega )}{P}_n(\text{cos}\theta ).\hfill \end{array}$$ (64)

III. RESULTS AND DISCUSSION

Equation (64) can be simplified using expressions for spherical Bessel and Hankel functions for small k_oa and k_oL: j_n(k_oa) ≈ (k_oa)ⁿ/[1 × 3 × ···(2n + 1)]; h_n(k_oLa) ≈ −i[1 × 3 × ···(2n − 1)]/(k_oL)ⁿ⁺¹. Thus an expression for the area deformation of a cell in the field of the resonance gas bubble has a concise form

$$\frac{\mathrm{\Delta }S}{S}(\omega ,\theta )=\frac{\mathrm{\Delta }R\cdot }{R_o}\frac{R_o^2}{a^2}\frac{R_o}{L}{\displaystyle \sum _{n=1}^{\infty }n(2n+1){\gamma }_o{\left(\frac{a}{L}\right)}^n\frac{d_S^n(\omega )}{d^n(\omega )}{P}_n(\text{cos}\theta ).}$$ (65)

The elastic properties of the bacteria are given in Table I. Results of the numerical calculations of the area deformation of different types of bacteria are given in Table II. These results are derived under the assumption that the cell moves and is deformed by the field of an oscillating bubble of resonance size. The intensity of the incident plane wave was assumed to be constant, and the relative displacement of the bubble was choosen as 0.5: ΔR/R_o = 0.5. To achieve such an amplitude of the microbubble osclillation at the resonance frequency, a low sound intensity (∼10 mW/cm²) is required. We also assume that the bubble is in contact with the cell: L = R_o + a. With increasing n, the deformation decreases as (a/L)ⁿ. However, if the difference in the density between the inner and outer liquids is small then the deformations on the dipole and quadrupole modes may be of the same order. Therefore, we restrict our investigation to only the dipole and quadrupole modes. For numerical calculations, the radius of the resonance of the bubble at a given frequency was derived from Eq. (59).

TABLE I.

Elastic shell properties of specific bacteria yeast cells: E is the Young’s modulus

Cell	E (MPa)	Poisson’s ratio	Radius (µm)	Thickness (nm)	T (N/m)	Turgor pressure (MPa)
E. colib	25	0.16	0.50	6	7.5 × 10−3	0.3
C. eugametosb			8	60	38	9.5
B. emersoniib			10	450	32	6.5
Yeastc	0.6	0.5	1.5–8
Yeastc	KA=12.9 (N/m)	0.5		90

^aReference [67]. Method: AFM.

^bReference [68]. Method: gas decompression

^cReference [69]. Method: AFM

^dReference [70]. Method: micromanipulation.

TABLE II.

Natural frequencies Ω₂, qualities of the quadrupole vibrations Q₂, maximal area deformation ΔS/S_max (n = 2), and the correspondent frequency f_max calculated for different types of bacteria.

Cell type	a (µm)	Ω2/2π (MHz)	Q2	fmax (MHz)	ΔS/Smax	Ro/a
E. coli	0.5	4.58	0.8	4.91	0.17	1.94
B. emersonii	10	2.24	15.8	2.17	0.01	0.19
B. yeast (AFM)	4.5	0.16	1.2	0.14	0.24	5.2
B. yeast (micromanipulation)	4.5	2.06	6.6	1.98	0.05	0.37

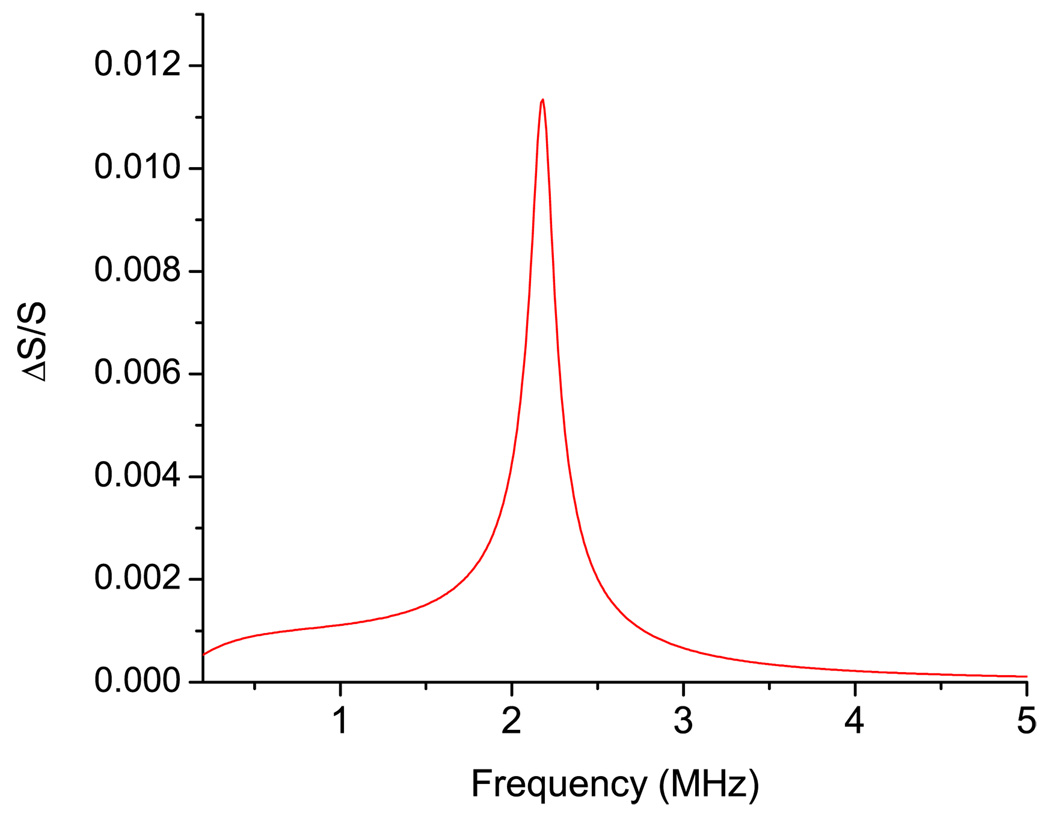
Figure 4 shows the area deformation of the B. emersonii cell in the vicinity of an oscillating bubble as a function of frequency for quadrupole mode (n = 2). For the quadrupole mode the deformation of the surface area decays as (1/L)³ for distance between the cell and bubble L. The dependence on the angle θ is given by Legendre polynomial P₂(cos θ) = 0.25 × (3 cos 2θ+1). The maximum of the deformation occurs at θ = π/4, at which P₂(cos π/4) = 1. Our numerical calculations show that the magnitude of the deformation on the dipole oscillations (n = 1) is smaller than the one for the quadrupole mode.

FIG. 4.

(Color online) Frequency dependence of the area deformation (n = 2) of the B. emersonii in the vicinity of an oscillating bubble calculated with the parameters from Table I.

The curve in Fig. 4 has a resonancelike shape with a strong peak at frequency f_max which is close to the frequency ω_K/2π (see Table II). At low frequencies (ω≪ω_K), the cell does not change its area during oscillations. At these frequencies the shell is subjected to only shear deformations. At high frequencies (ω≫ω_K), the influence of the surface elasticity is negligible, such that it behaves as a liquid viscous drop. According to the results presented in Table II, B. emersonii cells have a high quality factor (around 15) thus the shape of the frequency response curve (Fig. 4) is not surprising. Despite the fact that these cells might have high quality factors, the interaction with bubble at the resonance frequency should not result in visible mechanical or biological effects. At the maximum, the area deformation does not exceed 2%. Even red blood cells are able to sustain area deformations up to about 5% [21]. For the B. emersonii cell, the modulus K_A is approximately 64 N/m (Table I) and it was estimated that the maximum surface tension that the cell wall can sustain is 8 N/m [41]. For bacteria, the magnitude of the area deformation they can sustain is about 9%. It has been shown recently, that some bacteria can survive a 260 MPa pressure in a shock wave for a duration of 800 ns [42]. The main reason for such a weak effect of the vibrating bubble on the area deformation of the cell is that at the resonance frequency the radius of the bubble is not great enough to create a strongly inhomogeneous ultrasonic field in the vicinity of cell (Table I). For excitation of the natural vibrations of such cells, modulated radiation acoustical or optical force should be employed instead. Acoustic radiation force was used for excitation resonance oscillation of drops [12,13] and radiation force of the light was used for dynamic excitations of the bilayer vesicles [43].

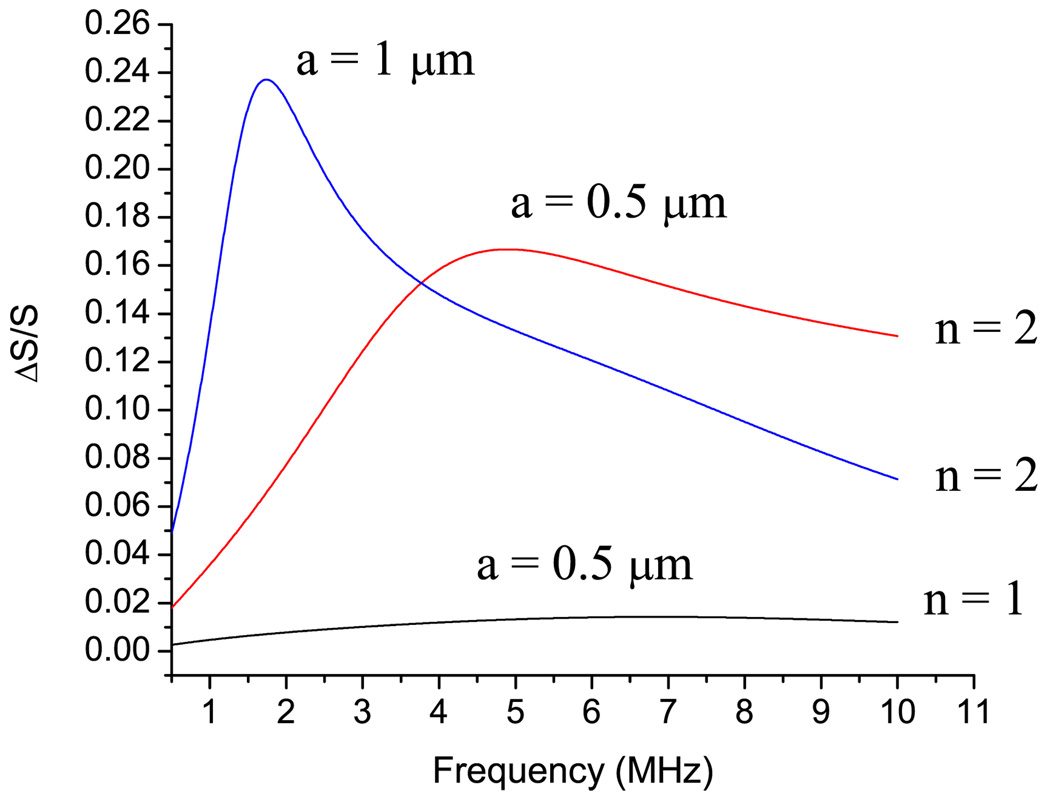
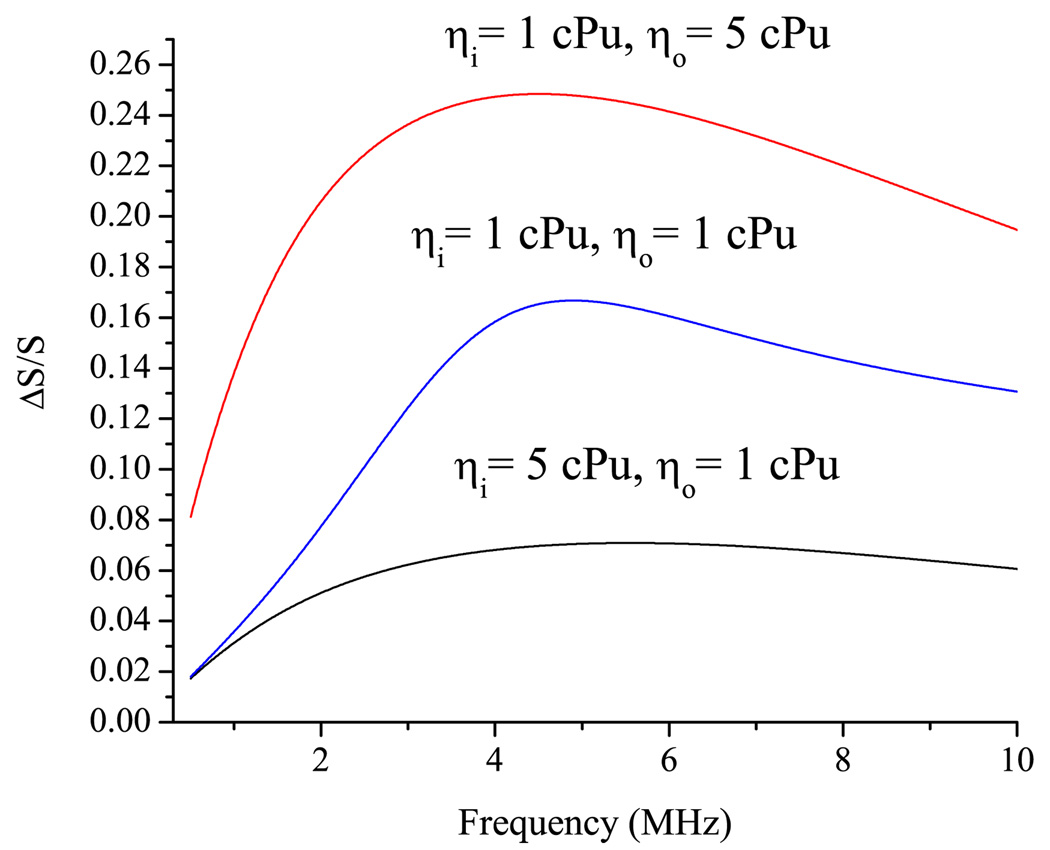
Consider behavior of a small cell, such as E. coli, in the field of a vibrating bubble. Behavior of E. coli in the sound wave should not have resonancelike behavior, since the quality of the natural vibrations of the E. coli cell is lower than 1 (see Table II). Figure 5 shows the relative area deformation of E. coli cell with the parameters taken from Table I. The relative area deformation of E. coli has a maximum at the frequency f_max which is close to the ω_K/2π. At the maximum, the area deformation of the 0.5 µm E. coli calculated to be 17%. Deformation of B. emersonii, which has a relatively high quality factor, is 17 times lower than that of E. coli. A similar tendency exists for yeasts cells which have a higher quality factor and a lower area deformation than those of E. coli. The explanation can be drawn from Table II. The last column in Table II shows the ratio between the radius of the oscillating bubble R_o and the radius of the cell a at the frequency of the mechanical resonance of the cell ω_K/2π. It can be seen that the value of the area deformation of the cell wall correlates to the ratio between the bubble radius and cell radius R_o/a. The higher this ratio, the higher the area deformation. Figure 5 shows the area deformation of E. coli with two radii: 0.5 and 1.0 µm. The deformation of the 1.0 µm cell at maximum is twice as high as for E. coli of 0.5 µm radius. It is in line with correlation discussed above: the ratio R_o/a for a 1.0 µm cell is higher than that of 0.5 cell: 2.29 and 1.94, respectively. Results for different values of the internal and external viscosity values are shown in Fig. 6. The increase of the internal viscosity causes a decrease of the deformation of the cell wall. With increases in the internal viscosity, the cell behaves more like a solid particle. Increase of the external viscosity has a different effect on the cell wall deformation: fivefold increases of the viscosity of the external fluid lead to the increase of the deformation by a factor of 2.

FIG. 5.

(Color online) Frequency dependence of area deformation of the E. coli in the vicinity of oscillating bubble calculated for two radii of the cell with the parameters taken from Table I.

FIG. 6.

(Color online) Frequency dependence of the area deformation (n = 2) of the E. coli in the vicinity of oscillating bubble calculated for different internal and external viscosities.

High amplitude thermal vibration of cells has been observed previously: vibration of the red blood cells (flicker) visible by an optical microscope has been detected by Brochard and Lennon [44]. The difference between flicker and the natural vibration of a bacteria cell is that in case of flicker no area deformation occurs. Flicker of a red blood cell is determined by the bending deformation of the membrane. In the case of a spherical bacterial cell, any variation of the cell shape leads to an area deformation. The effect of the area deformation on cell activity is not fully understood. In this report, we considered only the most obvious that of cell rupture. Relatively high area deformation may also influence transport processes within the cell and across the membrane. It was found recently that some cells with a strong wall, such as bakery yeast cells, had internal vibrations of the membrane at 1 KHz [45].

A direct experimental verification of the proposed theory might be conducted in the future; however, qualitative results have been obtained already. Some experimental studies on the mechanical effects of oscillating microbubbles on nearby cells have been conducted [46]. A recent study was done using a customized high-speed camera capable of recording 128 frames with a frame rate between 1 to 25 MHz visualizing the interaction between oscillating microbubbles and cells over a finite exposure period. It was reported that “a microbubble expansion of 100% resulted in a 2.3-µm displacement of the cell membrane,” sufficient to observe resonances of bacterial cells. Further experiments together with complementary theory such as that outlined in this paper are needed to more fully understand these complex interactions.

Rigorous modeling of the interaction of sound and cavitation with cells may establish the missing scientific foundations for bacteria death by ultrasound. Current research suggests that ultrasound is effective in killing bacteria [47–50], although the exact mechanisms are not well understood. At sufficiently high acoustic power inputs, ultrasound is capable of rupturing cells; moreover, ultrasonication is a well-established laboratory technique of cell disruption [51]. The calculations conducted for E. coli bacteria show that area deformation can reach 20%. This is sufficient deformation to rupture the cell wall.

Our simulations show that the area deformation of relatively large bacteria is not high enough (several percent) to rupture a cell wall; however, area deformation can be responsible for changing the transport processes of molecule across the cell wall. Other acoustically mediated effects are possible, which do not involve the immediate death of the cells. Ultrasound can enhance metabolic productivity of microbial cells in bioreactors [52] or membrane permeation (sonoporation) [53]. Under specific conditions, cavitational bubbles may cause the reversible disruption of the cell membranes facilitating the entry of molecules into cells [54,55], allowing for the enhanced drug delivery and other applications [56,57]. Ultrasound has successfully induced transfer of genetic material into living animals [58] and plant cells [59]. Further development of the theory of sound interaction with cells could eventually foster further development and optimization of these techniques.

The following setup allows verification of our theoretical approach. The theory fits the case of a microbubble attached to the bacteria or to any cell with spherical shape. Microbubbles or ultrasound contrast agents should bind to bacterial biofilms grown on a solid substrate. It is possible if microbubbles are targeted with ligands that bind specific receptors to the bacteria surface surface [60,61]. Ultrasound waves can be generated by a transducer attached to the solid substrate. Microbubbles several microns in size and possible rupture of a cell can also be detected by optical microscope. The imaging of vibration of the cell wall and acoustic quantification of a single bubble near an isolated cell is possible with high-speed CCD camera [46,62,63]. Since the bacteria’s cell wall is rigid, it may be difficult to visualize movement of the membrane in the vicinity of oscillating bubble. Other cells can be used for visualizing cell wall movements in the field of an oscillating microbubble. The HeLa cell is a good candidate for such experiments. HeLa cells become spherical during division [64] and their acoustical properties have been characterized [65]. Moreover, the HeLa celle were derived from cervical cancer cells, and cancer cells express a specific set of receptors, mainly receptors that encourage angiogenesis. Use of an appropriate ligand should allow binding of a microbubble to the HeLa surface. The movement of the cell wall in the vicinity of the microbubble can be detected with a high-speed CCD camera either with a transmission optical microscope or using the emulated transmission configuration described elsewhere [66].

IV. CONCLUSIONS

In this work, we investigate the oscillations of biological cells in a sound field generated by pulsating bubble using a shell model of the cell following an approach outlined previously [22]. Several conclusions can be drawn from the modeling of sound interaction with a biological cell: (a) the characteristics of a cell’s oscillations in an ultrasonic field are determined both by the elastic properties of the shell and the viscosities of all components of the system, (b) for dipole and quadrupole oscillations the cell’s shell deforms due to a change in the shell area and this oscillation depends on the surface area modulus K_A, (c) the relative change in the area has a maximum a frequency $f_k\sim \frac{1}{2\pi }\sqrt{K_A/(\rho a^3)}$.

Using this shell model the stress and tension in the bacterial shells within the close vicinity of a vibrating bubble are calculated. For bacteria with high value quality factors, the area deformation has a strong peak near a resonance frequency ω_K; however, the value of the deformation near the resonance frequency is not high enough to produce sufficient mechanical effect. Deformation of the cell wall is higher for smaller bacteria such as E. coli. At the frequency ω_K, the area deformation of E. coli with is high enough for cell rupture in the vicinity of an oscillating microbubble.

The model described can be used for (a) studying effects of the mechanical resonances of bacteria (tension and deformation in the bacteria shell) in the vicinity of bubbles or contrast agents in the surrounding liquid, (b) investigating the possibility of cell disruption at resonance frequency, and (c) understanding the effect of resonances on sonoporation in the ultrasound field, relating the area deformation in the ultrasound field and enlarged diameter of pores in the cell’s shells (membranes). However, the formulation can be extended to describe the deformation of a biological cell under any arbitrary, external periodic force including radiation forces induced by acoustical (acoustical levitation) or optical waves (optical tweezers).

APPENDIX A

For n = 0, only two boundary conditions are left (ρ_* = ρ_i):

$$-z_o{h}_o^{\prime }(z_o)A_0+z_i{j}_0^{\prime }(z_i)B_0=z_o{\epsilon }_0^{\prime }(z_o),$$ (A1)

$$\frac{{\rho }_o}{{\rho }_i}{h}_0(z_o)A_0-\left\{j_0(z_i)-\left[\frac{4K_A}{{\rho }_i{a}^3{\omega }^2}\right]z_i{j}_0^{\prime }(z_i)\right\}{B}_0=-{\epsilon }_0$$ (A2)

since $h_0^{\prime }(z_o)=-h_1(z_o)$ and $j_0^{\prime }(z_i)=-j_1(z_i)$

$$z_o{h}_1(z_o)A_0-z_i{j}_1(z_i)B_0=z_o{\epsilon }_0^{\prime }(z_o),$$ (A3)

$$\frac{{\rho }_o}{{\rho }_i}{h}_0(z_o)A_0-\left\{j_0(z_i)-\left[\frac{4K_A}{{\rho }_i{a}^3{\omega }^2}\right]z_i{j}_1(z_i)\right\}{B}_0=-{\epsilon }_0$$ (A4)

since z_ij₁(z_i) ≈ (z_i)²/3 and j₀(z_i) ≈ 1, then $j_0(z_i)-[\frac{4K_A}{{\rho }_i{a}^3{\omega }^2}]z_i{j}_1(z_i)\approx 1-\frac{4K_A}{{\rho }_i{a}^3{\omega }^2}\frac{{\omega }^2{a}^2}{3c_i^2}\approx 1-\frac{4K_A}{3a{\rho }_i{c}_i^2}$. The last term is small (≪ 1) and does not depend on the frequency. Therefore, cell’s shell does not signficantly affect the monopole oscillations of the cell in the acoustic field:

$$z_o{h}_1(z_o)A_0-z_i{j}_1(z_i)B_0=z_o{\epsilon }_0^{\prime }(z_o),$$ (A5)

$$\frac{{\rho }_o}{{\rho }_i}{h}_0(z_o)A_0-j_0(z_i)B_0=-{\epsilon }_0.$$ (A5′)

APPENDIX B

The functions 𝒥_n(ξ_i) and ℋ_n(ξ_i) are defined as follows:

$$\frac{{\xi }_i{j}_n^{\prime }({\xi }_i)}{j_n({\xi }_i)}=-\frac{{\xi }_i{j}_{n+1}({\xi }_i)}{j_n({\xi }_i)}+n=n-\frac{1}{{\mathcal{J}}_n({\xi }_i)},$$ (B1)

$$\frac{{\xi }_o{h}_n^{\prime }({\xi }_o)}{h_n({\xi }_o)}=\frac{{\xi }_o{h}_{n-1}({\xi }_o)}{h_n({\xi }_o)}-(n+1)=\frac{1}{{\mathcal{H}}_n({\xi }_i)}-(n+1).$$ (B2)

These functions can be calculated using the following iterative relations:

$${\mathcal{J}}_{n+1}({\xi }_i)=\frac{1}{[2n+3-{\mathcal{J}}_n({\xi }_i)]},$$ (B3)

$${\mathcal{H}}_{n+1}({\xi }_o)=\frac{1}{{\xi }_o^2}\left[2n+1-\frac{1}{{\mathcal{H}}_n({\xi }_o)}\right],$$ (B4)

where

$${\mathcal{H}}_0({\xi }_o)=-\frac{i}{{\xi }_o},$$ (B5)

$${\mathcal{J}}_0({\xi }_i)=\frac{1}{1-{\xi }_i\text{cot}{\xi }_i}.$$ (B6)