Interplay of Flavin's Redox States and Protein Dynamics: An Insight from QM/MM Simulations of Dihydronicotinamide Riboside Quinone Oxidoreductase 2

Abstract

Dihydronicotinamide riboside quinone oxidoreductase 2 is known to catalyze a two-electron reduction of quinone to hydroquinone using its cofactor, flavin adenine dinucleotide. Using quantum mechanical/molecular mechanical simulations, we have computed the reorganization free energies of the electron and proton transfer processes of flavin in the free state as well as when it is bound in the active site of the enzyme. The calculated energetics for electron transfer processes demonstrate that the enzyme active site lowers the reorganization energy for the redox process as compared to the enzyme-free aqueous state. This is most apparent in the two electron reduction step, which eliminates the possibility of flavosemiquinone generation. In addition, essential dynamics study of the simulated motions revealed spectacular changes in the principal components of atomic fluctuations upon reduction of flavin. This alteration of active site dynamics provides an insight into the `ping-pong' kinetics exhibited by the enzyme upon a change in the redox state of the enzyme-bound flavin. A charge perturbation analysis provides further support that the observed change in dynamics is correlated with the change in energetics due to the altered electrostatic interactions between the flavin ring and the active site residues. This study shows that the effect of electrostatic preorganization goes beyond the chemical catalysis as it strongly impacts the post-catalytic intrinsic protein dynamics.

1. Introduction

Dihydronicotinamide riboside (NRH): quinone oxidoreductase 2 (NQO2) and its close analog, dihydronicotinamide adenine dinucleotide phosphate (NADPH): quinone oxidoreductase 1 (NQO1) belong to a group of cytosolic enzymes, known as quinone reductases (QRs). QRs catalyze reduction of quinones to hydroquinones using the cofactor, flavin adenosine dinucleotide (FAD).^1–7 Regulation of these biomolecules in cells is linked to several important effects including cancer, release of oxidative stress, and in vivo conversion of anticancer prodrug to drug.^8–12 It has been observed that these enzymes are upregulated in cells in the presence of xenobiotics and antioxidants, thereby acting as an intracellular self-defense mechanism.¹³ These enzymes are also being targeted for their potential in prodrug therapy.^10,11 For example, CB-1954 is a prodrug that binds QR and recent studies have found that the catalytic conversion from prodrug to drug is faster in NQO2 than NQO1.⁹

The electron mediatory cofactor in these oxidoreductases is the tricyclic 7-,8-,10-substituted isoalloxazine ring, called flavin. The change in the flavin's redox state is believed to modulate the substrate binding and product release,^3,4,8,14 although, such modulation has remained incompletely characterized.⁸ It is known that the versatility of chemical functions in flavoenzymes originate due to flavin's unique ability to undergo both one- and two-electron reductions. Theoretical studies demonstrate that flavin's redox potential depends on the bend-angle of the flavin ring at the reduced state¹⁵ as well as on flavin ring substitutions.¹⁶ In the enzyme bound form, flavin's redox changes are influenced by the host enzyme's matrix.¹⁷ Active site residues create a set of noncovalent interactions that alters flavin's redox potentials facilitating the electron transfer process. However, it is not really known how the enzyme active site responds as flavin undergoes redox transitions. A molecular level characterization of the enzyme's response to flavin's redox changes therefore can provide valuable insight to the classic one-site `ping-pong' enzyme kinetics^8,14 of this enzyme.

One possible way to understand these inherent properties of flavoenzymes is to explore their redox properties and associated reorganization energies (λ). The reduction potential demonstrates the favorability of the reduction process, while λ is a measure of the intrinsic barrier of a redox system. It is defined as the hypothetical amount of energy required to distort the nuclear configuration of the reactant into the nuclear configuration of the product prior to the electron transfer.¹⁸ The role of an enzyme is attributed to its ability to lower λ by means of solvent polarization and electrostatic preorganization of the enzyme active site. Therefore, λ provides a measure of the intrinsic behavior of the enzyme active site as well as its impact on the energetics of the electron transfer processes. Although, experimentally it is difficult to determine these quantities, it is possible to use molecular simulations to compute them.^19,20 At the same time, these simulations also provide insights into the change of intrinsic dynamics of the active site. The dynamics of the active site is key in regulation of substrate binding and product release and hence is important in the `ping-pong' mechanism exerted by this enzyme. In our previous study,⁷ we calculated the redox potentials and pK_a of flavin in NQO2 using combined quantum mechanical/molecular mechanical (QM/MM) potentials,^7,15,21 which are in good agreement with the experimental results.²² Thus, in the present study, we have extended the QM/MM-based molecular dynamics simulation to examine the interplay of active site reorganization due to redox process and protein dynamics. A number of key residues were computationally mutated and their simultaneous effects on energetics and protein dynamics were studied. The reorganization energies, the features of essential dynamics during these processes, and their dependence on the electrostatic preorganization in the NQO2 active site are discussed.

2. Computational Methods

Free energies were computed using molecular dynamics simulations^23–25 with explicit solvent molecules. These simulations were carried out using the CHARMM²⁶ program suite with the CHARMM22^27,28 all-atom force field for the enzyme and cofactor. The three-point-charge TIP3P model²⁹ was used to treat water molecules. Nonbonded interactions were truncated using a switching function between 11 and 12 Å and the dielectric constant for the protein interior was set to unity. Bond lengths and bond angles of water molecules and bonds involving a hydrogen atom in the protein were constrained by the SHAKE algorithm.³⁰ In all molecular dynamics simulations, a time step of 1 fs was used in the leapfrog Verlet algorithm for integration.^31,32 Normal mode calculations of the protein were carried out using the coarse-grained approach.³³ The online server, http://ignmtest.ccbb.pitt.edu/cgi-bin/anm/anm1.cgi, was used to compute normal modes and simulate functional motions.^33,34 Essential dynamics^35,36 study was done through principal components analysis (PCA) using CARMA software.³⁷ All other computations were carried out on an in-house server containing 7 nodes, each with 8 Intel Xeon E5430 processors, located within the UWEC Chemistry Department. Visualizations of the protein structures as well as their geometric analyses were carried out using Visual Molecular Dynamics (VMD) software.³⁸

2.1. Coupled Electron-Proton Transfer Process

It is known that an electron transfer in flavin is promptly followed by a proton transfer.^39,40 In general, reduction of flavin may involve an incomplete one-electron reduction process yielding radical semiquinone,⁴¹ or a complete two-electron reduction to produce stable hydroquinone products.^42–44 Representing the NQO2-bound oxidized flavin as F, the first electron transfer process of the enzyme bound flavin produces a radical semiquinone, F^•−

$$\mathrm{F}+{\mathrm{e}}^{-}\to {\mathrm{F}}^{\cdot -}$$ (A)

The resultant semiquinone can be further reduced to hydroquinone F²⁻ or can abstract a proton

$${\mathrm{F}}^{\cdot -}+{\mathrm{e}}^{-}\to {\mathrm{F}}^{2-}$$ (B)

$${\mathrm{F}}^{\cdot -}+{\mathrm{H}}^{+}\to {\text{FH}}^{\cdot }$$ (C)

The protonated semiquinone undergoes a second electron transfer to form a more stable hydroquinone, FH⁻

$${\text{FH}}^{\cdot }+{\mathrm{e}}^{-}\to {\text{FH}}^{-}$$ (D)

For simultaneous two electron reduction, a dinegative hydroquinone is formed

$$\mathrm{F}+{2e}^{-}\to {\mathrm{F}}^{2-}$$ (E)

which can abstract a proton to form the stable hydroquinone, FH⁻

$${\mathrm{F}}^{2-}+{\mathrm{H}}^{+}\to {\text{FH}}^{-}$$ (F)

2.2. MD Simulations

The human quinone oxidoreductase 2 enzyme structure (PDB entry code: 1ZX1) was obtained from the protein data bank⁴⁵ and used in the MD simulations. Free energies for the electron and proton transfer reactions of NQO2 were computed through the implementation of Kirkwood's thermodynamic integration (TI) method^46,47 into the molecular dynamics simulations.^19,20 All necessary conditions for simulations including the partitioning scheme were maintained as described in the previous study.⁷ Briefly, the redox-active tricyclic isoalloxazine ring was treated with self-consistent charge-density functional tight binding (SCC-DFTB),^48–51 while embedded in a 30 Å thick layer consisting of molecular mechanically treated enzyme and solvent. The QM/MM boundary was treated by the link atom method.³⁵ Stochastic boundary conditions⁵² were employed to simulate enzyme solvent interactions. About 1500 ps of the stochastic MD simulation⁵² was run for each of the redox or protonation-deprotonation changes defined in eqs. A – F of which the last 500 ps data was used for further analysis (essential dynamics, see section 2.5).

2.3. Free Energy Calculations

For a particular redox process, if the two solvated redox states of the enzyme-bound flavins are designated as P and Q, then the total free energy change, ΔG^o (aq), is obtained as

$$\Delta G^{\text{TI}}\left(\mathit{aq}\right)={\int }_0^1{\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }_{\theta }d\theta$$ (1)

where U (θ) represents the intermediate hybrid potential energy functions that are constructed as linear combinations of the initial (P) and final (Q) state potentials, U_P and U_Q, respectively, so that

$$U\left(\theta \right)=(1-\theta )U_P+\theta U_Q$$ (2)

where θ is the coupling parameter that is varied in small intervals from 0 to 1. Separate MD simulations were carried out using linear response approximation at each intermediate value of θ and the total free energy difference was obtained through summation of the free energy changes over all intermediate intervals.^53,54 Furthermore, the ensemble-averaged partial derivative of the potential energy, with respect to the coupling parameter, θ, was computed for a specific value of θ in each simulation as follows:

$${\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }_{\theta }={\langle U_Q-U_P\rangle }_{\theta }$$ (3)

The reorganization free energy was obtained from ${\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }_{\theta }$ using

$${\lambda }^{\text{TI}}=\frac{1}{2}\left[{\langle U_Q-U_P\rangle }_P-{\langle U_Q-U_P\rangle }_Q\right]=\frac{1}{2}\left[{\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }_P-{\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }_Q\right]$$ (4)

2.3.1. Born Correction to the Free Energy

The free energy changes for both proton and electron addition were obtained from the thermodynamic integration method using stochastic boundary approximation and were corrected for electrostatic effects of atoms beyond 30 Å of the stochastic boundary (general Born's correction⁵⁵). Following Born's approach, the corrections applicable to the free energy of the electron and proton addition reactions can be calculated under the continuum approximation of a classical point charge of radius R in an infinite medium

$$\Delta \Delta G_{\text{Born}}=\frac{\left(\Delta q^2\right)}{2R}\left[1-{\frac{1}{\epsilon }}_{\text{st}}\right]$$ (5)

where Δq² is the difference of the square of charges of the two redox states and ε_st is the static dielectric constants of water, respectively. The analogous correction for reorganization free energy can be obtained from the difference of the charges (Δq) in the two redox states following the derivation of Ayala et al⁵⁶

$$\Delta \Delta {\lambda }_{\text{Born}}=\frac{\left(\Delta q^2\right)}{2R}\left[{\frac{1}{\epsilon }}_{\text{op}}-{\frac{1}{\epsilon }}_{\text{st}}\right]$$ (6)

and ε_op and ε_st are the optical and static dielectric constants of water, respectively.

For the electron addition reactions, λ^TI was obtained directly from the thermodynamic integration calculations. Therefore, the corrected reorganization free energies for the electron transfer reactions (reactions A and C) take the following form

$${\lambda }_{\text{corr}}^{\text{TI}}={\lambda }^{\text{TI}}+\Delta \Delta {\lambda }_{\text{Born}}$$ (7)

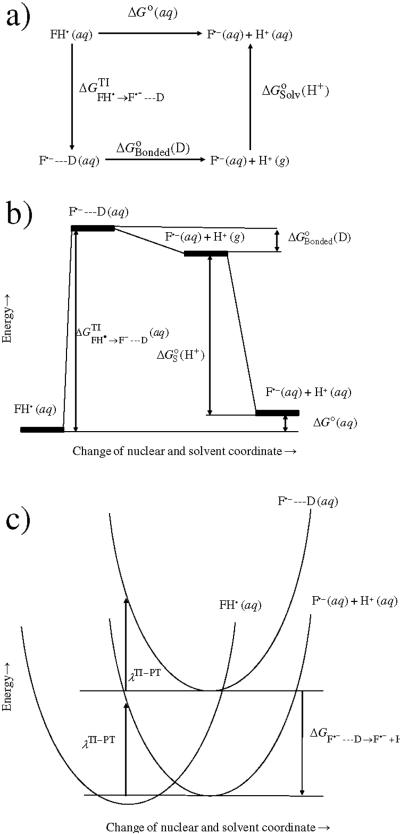
For the proton transfer reaction (reaction B), the reorganization energy was calculated as described below. The total aqueous state free energy of the proton transfer reaction was obtained using a thermodynamic scheme as shown in Fig. 1a:

$$\Delta G^{\mathrm{o}}\left(\mathit{aq}\right)=\Delta G_{{\text{FH}}^{\cdot }\to {\mathrm{F}}^{\cdot -}---\mathrm{D}}^{\text{TI}}\left(\mathit{aq}\right)+\Delta G_{\text{Bonded}}^{\mathrm{o}}\left(\mathrm{D}\right)+\Delta G_{\text{Solv}}^{\mathrm{o}}\left({\mathrm{H}}^{+}\right)$$ (8)

The first quantity in eq. 8 was obtained using thermodynamic integration in which the neutral flavosemiquinone (FH^•) is converted into an F^•−---D state, where the D is an uncharged dummy hydrogen atom. As discussed in the article of Li et al.,⁵⁷ the uncharged dummy atom has both bonding and van der Waal's interactions with F^•−, and only van der Waal's interactions with all other atoms. The bonding component $\left(\Delta G_{\text{Bonded}}^{\mathrm{o}}\left(\mathrm{D}\right)\right)$ only contributes to the free energy change for converting the dummy atom to a gas-phase proton (Fig. 1b) and its value is known from previous calculations.^7,15,58 Finally, the third quantity, $\Delta G_{\text{Solv}}^{\mathrm{o}}\left({\mathrm{H}}^{+}\right)$, is another known quantity – the solvation free energy of a free proton.

Figure 1.

Reorganization free energy calculations for the F^•− →FH^• process: a) a thermodynamic scheme, b) a diagram showing energy levels of intermediates used in the calculation, c) potential energy surfaces and reorganization energy for the reaction.

The first step of the proton transfer consists of the reorganization of the protein and solvent in response to the abolition of the positive charge. In the present study, the reorganization of proton transfer has been made equal to the reorganization free energy of the reaction FH^• → F^•−---D. Since the dummy atom has no electrostatic interaction with F^•−, the reorganization of the system for a change of F^•−---D(aq) to F^•−(aq) + H⁺(g) will be negligibly small and has been ignored. Finally, the solvation of the proton will involve a vertical drop of free energy change as it would require no further reorganization to add a proton into the edge of a solvated system that is infinitesimally spread out (Fig. 1c). Similar to the electron addition process, the Born correction was added to account for the effect due to an infinitesimally spread out solvent. The corrected reorganization free energy for the proton transfer reaction was therefore computed using the same eq. 6 as used in the case of an electron transfer reaction.

For each chemical process described in 2.1, the propagated error was computed from the uncertainties (standard deviation of $\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle$) for individual flavin states involved in the process.

2.4. Normal Mode Simulation

Normal mode analysis (NMA) was performed as described earlier.⁵⁹ Briefly, NMA was carried out using the coarse-grained elastic network model.^33,60,61 We used the Anisotropic Network Model (ANM), where the protein is simplified to a string of beads.⁶² Each bead represents a Cα atom. In ANM, the fluctuations are anisotropic and the overall potential of the system is expressed as the sum of harmonic potentials between the interacting C_α atoms.

$$V_{\text{ANM}}=\frac{\lambda }{2}\left[\sum _{j,i\ne j}{\Gamma }_{\mathit{ij}}\left[{(r_{\mathit{ij}}-r_{\mathit{ij}}^{\mathrm{o}})}^2\right]\right]$$ (9)

In eq. 9, γ represents the uniform spring constant, $r_{\mathit{ij}}^{\mathrm{o}}$ and r_ij are the original and instantaneous distance vectors between residues i and j, and Γ_ij is the ij-th element of the binary connection matrix of inter-residue contacts. Based on an interaction cut-off distance of r_c, Γ_ij is equal to 1 if $r_{\mathit{ij}}^{\mathrm{o}}$ < r_c and is zero otherwise. In the present study, normal mode calculations were performed on the cofactor-free enzyme, its three dimensional coordinates obtained from the crystal structure of dimeric human quinone oxidoreductase 2 (residues 1–234, pdb code: 1QR2). The optimal cutoff and distance weight for interactions between the C_α atoms were kept at 18 Å and 2.5 Å, respectively in the present study.³³

2.5. Essential Dynamics

The essential dynamics^35,36 (ED) of the protein was extracted by examining the protein's principal components using the program CARMA.³⁷ The calculation of principal components involve eigenvalue decomposition of a covariance matrix of the mass-weighted atomic displacements, the mathematical formulism is described elsewhere.⁶³ Briefly, the covariance matrix, C, with elements C_ij for any two points (C_α coordinates) i and j is computed using

$$C_{\mathit{ij}}=\langle (x_i-\langle x_i\rangle )(x_j-\langle x_j\rangle )\rangle$$ (10)

Where x₁, x₂ …, x_3N are the mass-weighted Cartesian coordinates of an N-particle system and the angular brackets represent an ensemble average calculated over all sampled structures from the simulations. Next, the symmetric 3N×3N matrix C can be diagonalized with an orthonormal transformation matrix R

$${\mathbf{R}}^{\mathbf{T}}\mathbf{CR}=\text{diag}(v_1,v_2,\dots ,v_{3N})$$ (11)

Where v₁, v₂,…,v_3N represent the eigenvalues and the columns of R are the eigenvectors, which are also called the principal modes. If X(t) represents the time-evolved coordinates (trajectory) of the water-encapsulated protein active site, it can be projected onto the eigenvectors

$$q={\mathbf{R}}^{\mathbf{T}}(\mathrm{X}\left(t\right)-\langle \mathrm{X}\rangle )$$ (12)

The projection is a measure of the extent (mean square fluctuation) to which each conformation is displaced, in the direction of a specific principal mode, and called principal components (PCs). For a trajectory, the projections are obtained as matrix elements q_i (t), i = 1, 2,…, 3N.

The PCA was carried out using the following steps: (i) preparing a modified trajectory file from the original MD simulation trajectory file by removing the coordinates of the water molecules, removing the overall translational and rotational motions, and using only the C_α atoms, (ii) the calculation of the covariance matrix, in which the fluctuations in the C_α atomic coordinates were the variables, and (iii) the diagonalization of the covariance matrix for the calculation of the eigenvectors and the corresponding eigenvalues. The root mean square projections (RMSP) of q were obtained by computing the root mean square average over all M conformations obtained from the 500 ps simulations:

$$\mathit{RMSP}=\sqrt{\frac{1}{M}\sum _{i=1}^{\text{conf}}{\left[q_i\left(t\right)\right]}^2}$$ (13)

To determine if the functional dynamics had undergone significant change before and after a chemical process, a combined essential dynamics analysis was performed following literature methods.^64,65 Following this procedure, a comparison of the dynamics of two or more systems, was carried out by concatenating the individual simulation trajectories, producing a combined covariance matrix. The separate trajectories were then projected onto the resulting eigenvectors and the properties of these projections were compared and contrasted.

2.6. Charge Perturbation Analysis

The contributions of individual charged residues on energetics and dynamics were obtained by charge perturbation calculations. The effect of a charged residue on the energetics was computed by the annihilation of partial charges (indicated by δ) of all atoms of that specific residue and by computing the charge-deletion induced change of the ensemble-averaged potential energy derivative with respect to the coupling parameter θ, $\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle$, over 500 ps of simulation time:

$$\Delta E_{\text{elec}}={\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }^0-{\langle \frac{\partial U\left(\theta \right)}{\partial \theta }\rangle }^{\delta }$$ (14)

In order to evaluate the contribution of a specific residue to the overall energetics of the reaction F + 2e⁻ + H+ → FH⁻, the difference of the two ΔE_elec s was computed

$$\Delta \Delta E_{\text{elec}}=\Delta E_{\text{elec}}\left({\text{FH}}^{-}\right)-\Delta E_{\text{elec}}\left(\mathrm{F}\right)$$ (15)

Therefore, ΔΔE_elec is the electrostatic stabilization energy of FH⁻ relative to F, due to partial charges of all atoms in a specific residue. The contribution of these charged residues on dynamics was also determined from their effect on RMSP, which was calculated using eq. 13, of a PC1 derived from a combined analysis (subsection 2.3) of trajectories before and after removing their partial charges, δ. For a specific redox state of enzyme-bound flavin, the effect of a charged residue on the dynamics was calculated from the difference in RMSP:

$$\Delta {\mathit{RMSP}}_{\text{elec}}={\mathit{RMSP}}^0-{\mathit{RMSP}}^{\delta }$$ (16)

The relative contribution of the partial charge of a specific residue to the dynamics of the overall reaction F + 2e⁻ + H⁺ → FH⁻, was computed from the ΔRMSP_elec of the two end states F and FH⁻:

$$\Delta \Delta {\mathit{RMSP}}_{\text{elec}}=\Delta {\mathit{RMSP}}_{\text{elec}}\left({\text{FH}}^{-}\right)-\Delta {\mathit{RMSP}}_{\text{elec}}\left(\mathrm{F}\right)$$ (17)

3. Results and Discussion

3.1 Energetics of Reorganization

In this study we have computed the reorganization free energy of the electron and proton transfer reactions for both the flavin in aqueous solution and in the active site of the NQO2 enzyme using SCC-DFTB/MM simulations. The SCC-DFTB method involves a self-consistent-field treatment of electron-electron interactions into tight-binding theory.⁶⁶ In addition, the electronic polarization is approximated by first order perturbation in terms of atom-centered point charges obtained by Mulliken population analysis.^50,51 SCC-DFTB/MM has successfully produced reliable geometry and energetics^7,15,58,67 for the flavin systems, where each occurrence of an electron transfer is strongly correlated to a proton transfer.⁶⁸ Recently, SCC-DFTB has been used to determine the redox potentials of free flavin (lumiflavin)¹⁵ as well as three well characterized flavoenzymes: medium chain acyl-CoA dehydrogenase,¹⁵ cholesterol oxidase,¹⁵ and quinone oxidoreductase 2.7 These results are in close agreement with the experimentally determined redox potentials.^7,15 Furthermore, density functional theory based calculations have been performed on flavin systems,^15,44 including those by our group with new generational density functionals¹⁶ in particular, which indicate that the quantum mechanical treatment with SCC-DFTB is capable of producing satisfactory energetics for the flavin systems.

Although, determination of the extent of coupling between these two transfer processes has not been attempted, the present study provides details of the energetics of the electron and proton transfer reactions detailed in subsection 2.1. The impact of the NQO2 enzyme matrix on these energetics is also discerned by comparing analogous quantities from the simulation of the lumiflavin-water system.

The computed reorganization energies associated with the electron and proton transfer reactions for both the free flavin (lumiflavin) as well as the NQO2-bound flavin in water are listed in Table 1. The ${\lambda }_{\text{corr}}^{\text{TI}}$ values for the single electron addition reactions (processes A, B, and D) range between 50–65 kcal/mol, while for proton transfer reactions (C and F) ${\lambda }_{\text{corr}}^{\text{TI}}$ varies between 53–81 kcal/mol. It is also apparent from Table 1 that a significantly large reorganization energy (248 and 191 kcal/mol, respectively, for the free and the NQO2-bound flavin) is required for the single-step two-electron addition reaction (process E).

Table 1.

Various free energy components of the electron and proton transfer reactions of lumiflavin and NQO2-bound flavin (in parenthesis) in aqueous solution. The total reorganization energy was computed using eq. 7. All energies are given in kcal/mol. For λ_Born, the optical and static dielectric constants used were 5.5 and 75.0, respectively. The statistical error was found to be 0.2–0.3 kcal/mol.

Reactions	Process	λTI Free (enzyme)	λ Born	${\lambda }_{\text{corr}}^{\text{TI}}$ Free (NQO2)	Free energy of reaction ΔG°(aq)	Lowering of Reorganization Energy by Enzyme
F + e− → F·−	A	61.8(51.5)	0.9	62.7 (52.4)	−93a (−90a)	10.3
F·− + e− → F2−	B	62.2 (50.3)	2.8	65.0 (53.1)	−118a (−87a)	11.9
F·− + H+ → FH·	C	63.9 (52.3)	0.9	64.8 (53.1)	−8 (−3)	11.7
FH· + e− → FH−	D	61.1 (49.5)	0.9	62.0 (50.4)	−97a (−101a)	11.6
F + 2e− → F2−	E	244.1 (187.2)	3.7	247.8 (190.9)	−214 (−178)	56.9
F2− + H+ → FH−	F	77.9 (55.0)	2.8	80.7 (57.8)	17a (−19)	22.9

It has been suggested that the role of the enzyme as catalyst is primarily to reduce this reorganization cost, facilitating the reactant to cross over to the product state.⁶⁹ Comparison of both electron and proton transfer energetics for the free vs. enzyme-bound flavin clearly demonstrates that the NQO2 enzyme matrix is able to lower the reorganization cost for these reactions. For example, in reactions A–D, the NQO2 active site lowered the reorganization energy by ~10–12 kcal/mol (Table 1). However, the most dramatic effect of the enzyme is evident in the simultaneous two-electron transfer reaction (process E) and the subsequent proton transfer reaction (process F). As indicated in Table 1, for the transformation F →F²⁻, the NQO2 active site was able to lower the reorganization energy by ~57 kcal/mol (~23%) compared to the aqueous lumiflavin. Furthermore, a 23 kcal/mol (28%) decrease of λ was observed for the proton transfer to the dinegative hydroquinone (process F) (Table 1).

Although, the F + 2e⁻ →F²⁻ energetics have been analyzed in the current study, the biologically more relevant state is FH⁻.⁷ Moreover, for NQO2 enzyme, the free energy change for the F²⁻ + H⁺ → FH⁻ process is −19 kcal/mol,⁷ indicating that F²⁻ is a highly unstable intermediate. Therefore, F²⁻ is omitted for further analysis of protein dynamics.

The computed reorganization energies for the electron and proton addition steps demonstrate a clearer role of the enzyme active site when compared to the aqueous state. However, the effect of enzyme environment is not so noticeable on the favorability of flavin's reduction. The overall free energy changes (ΔG^o (aq)) for the F + 2e⁻ + H⁺ → FH⁻ reaction are −194 and −196 kcal/mol, respectively, for the aqueous vs. enzyme-bound systems (Table 1), indicating only 2 kcal/mol advantage in enzyme over aqueous environment. Therefore, the present study shows that the role of the active site in NQO2 is limited to lowering of the reorganization energy in order to facilitate the two-electron reduction.

3.2. Functional Protein Dynamics

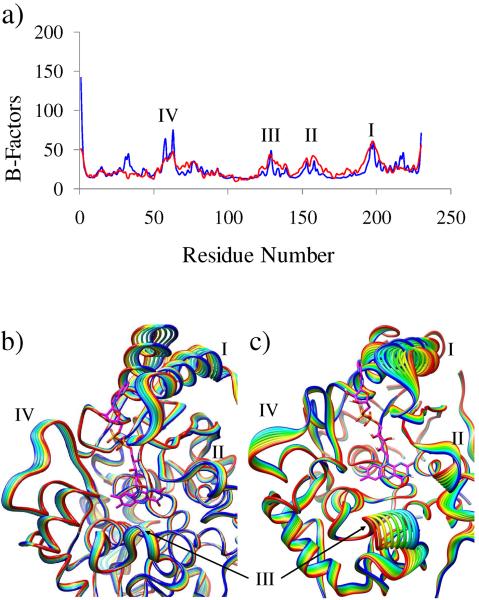
To explore functional protein motion in NQO2, the flexible regions of the system were first identified by normal mode analyses. The B-factors (thermal fluctuation of C_α atoms about their mean position) calculated from normal mode analysis were quite comparable to those obtained from the X-ray structure (Fig. 2a), indicating that these low-frequency normal modes produced reliable representations of the protein dynamics. However, the theoretical framework of normal mode is based on coarse-grained assumption and is therefore unable to reproduce the response of the active site due to the redox changes of the cofactor. To identify the impact of the electron transfer on the slow enzyme dynamics, essential dynamics (ED) calculations were carried out using the stored conformations of the atomistic MD simulations.

Figure 2.

Functional motion identified through normal mode and MD simulations: a) comparison of the B-factors between X-ray crystallography (red) and NMA-derived normal modes (blue), where all 1–10 low-frequency modes were taken into account to compute the B-factors; b) the lowest frequency normal mode observed for the NQO2; and c) the principal component 1 in the essential dynamics analysis performed using the trajectory of the free energy simulations. In b) and c) only the backbone C_α atoms for 10 conformations are shown for clarity. The four regions that exhibited major thermal fluctuations are I, loop-helix motif (Ala191–Glu217); II, loop (Gly149–Asn161); III, loop (Ala125–Leu137); and IV loop (Ile55 –Phe65).

As shown in Fig. 2b–c, the simulated normal mode 1 obtained from NMA of the enzyme-bound neutral oxidized flavin state is quite comparable to that of the principal component 1 obtained from ED. Both simulations revealed identical protein segments that are involved in dynamics. The four significantly mobile regions (Fig. 2) identified in this study are: I, loop-helix motif (Ala191-Glu217); II, loop (Gly149-Asn161); III, loop (Ala125-Leu137); and IV, loop (Ile55-Phe65). This comparison demonstrates that atomistic (ED) and coarse-grained (NMA) simulations present essentially the same features of the protein dynamics in the flavoenzyme.

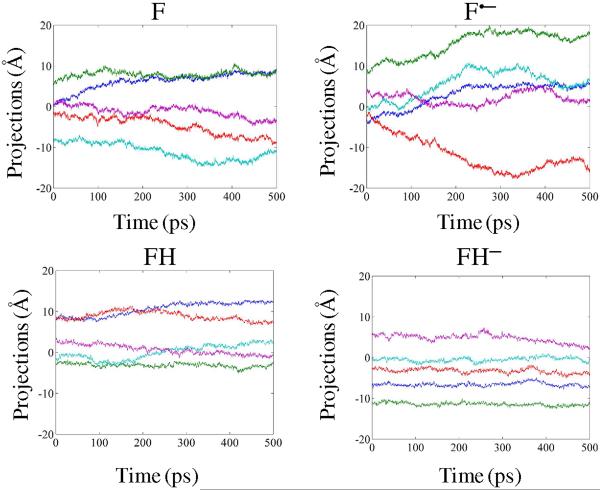
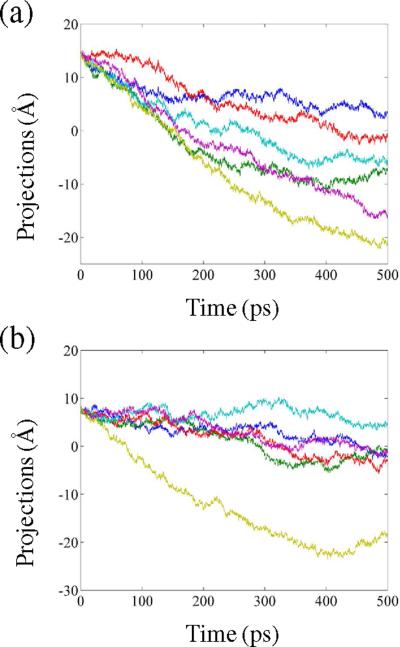
Dynamics is an intrinsic property encrypted in the three-dimensional structure and folding of a protein.⁵⁹ An enzyme catalyzed chemical event is also related to a protein's dynamics.^70,71 To explore if the change in the redox states of NQO2 has any effect on the intrinsic enzyme dynamics, we computed the essential dynamics of the flavin-bound enzymes at differing redox and/or protonated states. Specifically, the trajectories of the C_α atoms of all four states viz. F, F^•−, FH^•, and FH⁻ were combined and the combined trajectory was projected to their principal components. Analysis of the essential dynamics (Fig. 3) clearly shows that each redox or protonation state has a distinct set of principal components. In particular, the enzyme bound state of the anionic flavin semiquinone (F^•−) exhibits a huge displacement of the first 5 principal components (Fig. 3). The observed change of 10–20 Å (Fig. 3) evidently portrays a highly dynamic and NQO2 active site within the semiquinone state.

Figure 3.

Projections of the simulation frames onto the first 5 principal components color coded as PC1 (blue), PC2 (green), PC3 (red), PC4 (cyan), and PC5 (purple) for the various redox states of flavin.

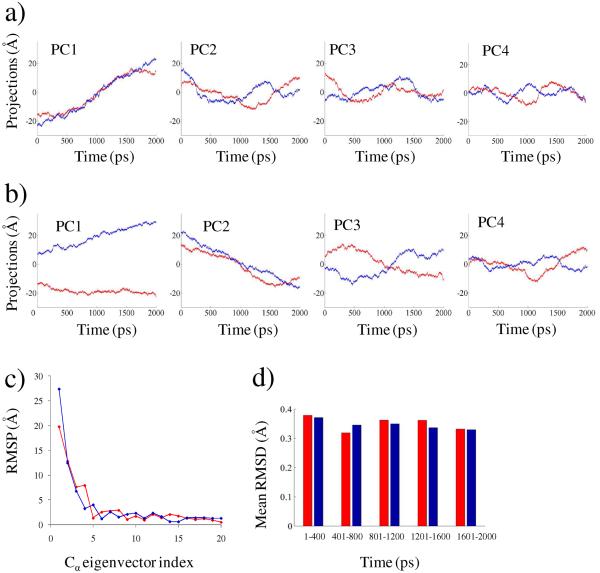
A combined vs. separate analysis was carried out using 2 ns MD trajectory (Fig. 4) of the enzyme-bound flavin systems for both of the biologically relevant redox states (i.e. F and FH⁻). This analysis demonstrates that although indistinguishable in the separate analysis (Fig. 4a), the fluctuations of the two active sites exhibit considerable differences when projected onto common principal components (Fig. 4b). The RSMP (eq. 13) of the first 20 eigenvectors for the last 500 ps of the 2 ns simulations is shown in Fig. 4c. The first as well as the fourth mode in the combined analysis clearly showed a large difference (> 5Å). The comparison shows that there exists significant difference in major principal components of dynamics between the enzyme-bound neutral flavin and the anionic flavohydroquinone states. This observation is the first ever report of a change in the functional dynamics of a protein due to the change in its cofactor's redox state. The stability of the dynamics was checked from the mean root mean square deviations (RMSD) of all C_α-C_α distances sampled over each 400 ps segment of the simulation data. The mean RMSDs vary within 0.1 Å (Fig. 4d), indicating that these systems are quite stable and suitable for ED analysis.

Figure 4.

Separate versus combined ED analysis showing altered dynamics of the flavin-bound NQO2 enzyme system. The enzyme-bound flavin in the oxidized (F) state is shown in red, while the reduced (FH⁻) state is shown in blue for a) separate ED analysis, b) combined ED analysis, c) computed RMSPs (eq. 13) over the last 500 ps of simulation data for the eigenvectors 1–20, and d) computed mean RMSDs of all Cα-Cα distances sampled over 400 ps simulation data.

It is known that NQO2 involves `ping-pong' kinetics, where two substrates share a single active site and substrate binding/product release is regulated by flavin's redox state. The NQO2 active site is likely to involve altered dynamics as an aid to the substrate recognition process. The present models are based on substrate-free states and cannot predict the energetics of substrate-bound enzymes, nonetheless it is fair to conclude that the redox transition of flavin certainly triggers a change in the intrinsic dynamics and is likely to pave the way for the substrate shuttling involved in the `ping-pong' kinetics.

3.3. Electrostatic Preorganization and Protein dynamics

It is generally believed that catalysis occurs under optimized protein electrostatics (electrostatic preorganization) that minimize the reorganization energy.^69,72 These electrostatic interactions are expected to influence the enzyme's conformational space and are likely to shape the dynamics of the electron-proton transfer process. Therefore, the key functional properties of an active site is essentially encrypted into its signature electrostatic preorganization.⁶⁹ If the partial charges of any one of these residues are voided, the behavior of the active site will be altered. If the dynamics of the active site is linked to the energetics of flavin's redox changes, then the charge perturbation would simultaneously impact the dynamics and energetics of the system. To probe this hypothesis, five active site residues (Glu193, Lys113, Asp117, Arg118, and Tyr155) were chosen and their effects on protein dynamics, as well as energetics, were examined. The location of these residues with respect to the flavin ring is shown in Fig. 5. These residues are close to the dynamic segments of the protein identified by the NMA and MD simulations and they have moderate-to-strong impact on the relative stability of the flavin's redox states.⁷ Glu193 is in the loop-helix motif (Ala191- Glu217), wheras Lys113, Asp117, and Arg118 are attached to a helix that is an extension to the dynamic region III (loop Ala125-Leu137) (Fig. 5). Finally, Tyr 155 is part of region IV (loop Gly149-Asn161). Tyr155 makes a hydrogen bonding interaction with an exocyclic flavin ring oxygen. In the subsequent study, a charge-perturbation analysis was carried out, where the charges of the above mentioned five residues were abolished and each perturbation's impact on the dynamics and energetics of the protein was studied.

Figure 5.

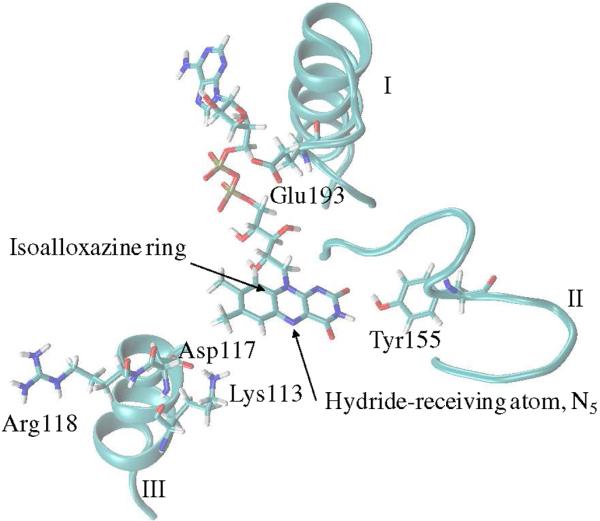
Location of five active site residues shown relative to the flavin (isoalloxazine) ring of FAD and the dynamic regions as described in the text (subsection 3.2).

3.3.1. Impact of Partial Charges of Individual Residues on Energetics

The effect that a partial charge of a specific residue has on energetics, ΔE_elec, was computed from the ensemble average partial derivative of the potential energies (eq. 14). Since we are interested in the relative measure of the impact, the difference of the impacts between the two enzyme states, F and FH⁻, ΔΔE_elec was computed (eq. 15, Table 2). The computed ΔΔE_elec values of Lys113 and Arg118 are −4.9 and −2.4 kcal/mol, respectively, indicating that these two charged residues relatively favor the oxidized state (F). Interestingly, the charges of Asp117 and Tyr155 favored the reduced state (FH⁻) by 3.7 and 2.3 kcal/mol, respectively, compared to the oxidized state (F). Although it appears to be counter-intuitive, our earlier calculations demonstrated that the pK_a of the NQO2-bound neutral hydroquinone state, FH₂, is extremely low and is close to 0.⁷ If the FH₂ is considered as a weak acid, then the negative charge bearing residues (Brønsted bases) can favor the deprotonation of FH₂. Conversely, positive charge-bearing residues will behave as Brønsted acids and therefore will favor the protonation of the anionic FH⁻. This suggests that charged residues have critical role in active site polarization of the enzyme-bound flavin.

Table 2.

Computed ΔΔE_elec and ΔΔRMSP values were obtained from a charge-perturbation calculations (see subsection 3.3). The distances of the residues from the redox site were calculated from the distances of their individual C_α atoms from the N5 atom on the flavin ring (Fig. 5).

Residues	Distance from the redox site (Å)	ΔΔEelec (kcal/mol)	ΔΔRMSP (Å)
Asp117	7.5	3.7	−0.8
Arg118	10.4	−2.4	4.9
Lys113	11.0	−4.9	4.1
Glu193	12.2	0.1	−1.7
Tyr155	14.1	2.3	−0.9

3.3.2. Impact of Partial Charges of Individual Residues on Dynamics

Removal of partial charge from an individual residue and its impact on principal components was also studied using the same trajectories of motion. Conformations of these perturbed dynamics were stored, and the impact on the first principal component was examined (Fig. 6a, b). As evident from the figure, abolition of charges had dissimilar impacts on the protein dynamics of the enzyme-bound neutral flavin state (Fig. 6a) compared to the anionic flavohydroquinone state (Fig. 6b). The latter is the hydride transfer state of the NQO2-bound flavin and the analysis demonstrates far lesser impact due to the charge perturbations on its dynamics as compared to the neutral state.

Figure 6.

Projections of the simulation frames onto the first principal component of a) oxidized (F) and b) reduced (FH⁻) states derived from the combined trajectories of 5 charge perturbed residues and the wild-type enzyme (see subsection 3.3 for discussion). Various charge perturbed residues are color-coded as the wild-type (blue), Asp117 (green), Tyr155 (red), Lys113 (cyan), Glu193 (purple), and Arg118 (olive).

For a specific redox state of the enzyme, the impact due to the partial charge of an individual residue can be quantified by computing the difference of theirs individual RMSP s before and after the charge is abolished (i.e. ΔRMSP eq. 16). ΔRMSP can be regarded as a quantitative way to measure the electrostatic effect of the partial charge of a specific residue on the dynamics of a particular redox state of the enzyme in the direction of a chosen principal component. A positive value of ΔRMSP indicates that the charge of the residue resisted a deformation in the direction of the principal component 1 obtained in the combined essential dynamics analysis. In order to compare how the same residue impacts the reduced (FH⁻) state relative to the oxidized (F) state, ΔΔRMSP s are computed using eq. 17 (Table 2). The calculations reveal that positively charged residues produce positive ΔΔRMSP values, indicating that these residues create resistance to the dynamics of the reduced hydroquinone state (FH⁻) relative to the neutral oxidized (F) state. Conversely, negatively charged residues had negative ΔΔRMSP values, which indicate that these charged residues hindered the deformation along PC1 of the neutral oxidized state (F) of the enzyme-bound flavin.

3.3.3. Correlation of Dynamics and Energetics

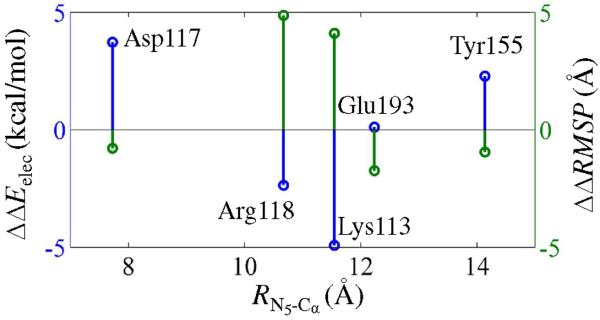
Finally, the effects of individual charged/polar residues on the energetics and dynamics were studied by comparing ΔΔRMSP and ΔΔE_elec. A plot of these quantities and the distance of separation from the hydride receiving atom, N5, is shown in Fig. 7.

Figure 7.

Computed ΔΔE_elec and ΔΔRMSP values (eqs. 15 and 17) of residues plotted against the average distance of separation of their individual C_a atoms from the N₅ atom on the flavin ring.

The present study shows that the reduction of enzyme bound flavin has significant impact on the electrostatic interactions of the flavin with all the above mentioned residues. This is revealed in Fig. 7. In particular, Glu193, Asp117, and Tyr155 were found to stabilize the reduced flavin (FH⁻) state exhibiting positive ΔΔE_elec and negative ΔΔRMSP (Table 2) while positively charged residues, Lys113, and Arg118, were found to disfavor the reduction with negative ΔΔE_elec and positive ΔΔRMSP.

This study also demonstrates that the stabilizing electrostatic interactions create a favorable dynamics, whereas the destabilizing residues tend to resist deformations. This is evident from the negative ΔΔRMSP obtained for the electrostatic interactions (Glu193, Tyr155, and Asp117) that stabilizes the flavohydroquinone state and vice versa. This is quite enlightening as it supports the idea that key electrostatic residues influence the dynamics of the enzyme active site to acquire conformational spaces that are thermodynamically favored. Therefore, the present results show that the electrostatic preorganization plays a key role in shaping the observed dynamics of this enzyme. As the enzyme-bound flavin oscillates through the redox cycle, the active site's electrostatic polarization responds by altering the dynamics.

The observed results are in excellent agreement with the experimental results. The role of Glu193 has been previously observed in substrate binding.⁷³ Lys113 has been found to be a critical residue in flavin's function as a redox mediator. A mutation of Lys113 to Alanine completely impairs the protein's ability to function.⁷⁴

4. Conclusion

Using QM/MM simulations, we have computed the reorganization energies of the redox and protonation/deprotonation reactions of the flavin-bound NRH:quinone oxidoreductase, and compared them with the energetics of the flavin in aqueous solution. The reorganization energy was computed using linear response approximations of the thermodynamic integration approach implemented with MD simulations. The obtained trajectories from MD simulations for flavin-bound enzymes at their differing electronic states were analyzed using a principal component analysis method. The trajectories were projected onto common principal components and the effect of the flavin's redox and protonation/deprotonation equilibria on the enzyme's dynamics were explored. A charge perturbation analysis was also carried out, which provides insight to the effect of electrostatics on energetics and dynamics.

These calculations show that a significant amount of reorganization energy is required for simultaneous transfer of two electrons (Table 1) to the bound flavin ring. However, it also demonstrates that the enzyme matrix lowers the reorganization cost by a significantly large quantity (57 kcal/mol) for two-electron transfer process. This is a much greater decrease in reorganization cost than the decrease observed in single electron transfer, which ranges between 10–11 kcal/mol. Furthermore, it is evident that the lowering of the reorganization cost in NQO2 for subsequent addition of a proton to the dinegative hydroquinone species is also high with a value of ~23 kcal/mol.

Analysis of the essential dynamics shows that the dynamics of the enzyme active site undergo perceptible changes due to the redox transition. Fluctuations obtained in this study by projecting these trajectories onto common principal components exhibit spectacular differences in the conformations of the same active site, each with differing redox and protonated states of the flavin. Analysis of the two biologically relevant states, the neutral F and the hydride (2e⁻/1H⁺) transferred FH⁻, reveals that hydride transfer significantly alters the dynamics of the active site.

Finally, the charge perturbation analysis conclusively demonstrates that the observed differences in the essential dynamics are rooted to the electrostatic interaction between the cofactor and the active site charged residues. It demonstrates that as the flavin shuttles between neutral (F) to reduced form (FH⁻), the electrostatic interactions undergo changes that are reflected in the energetics as well as in the intrinsic dynamics. Therefore, the study demonstrates that the effect of electrostatic preorganization goes far beyond catalysis. It impacts the intrinsic dynamics of the enzyme, which is expected to regulate the substrate shuttling. Taken together, this study provides a comprehensive picture of how flavin's redox state fine-tunes the dynamics and paves the way for a “ping-pong” mechanism.