A Piecewise Patch-to-Model Matching Method for Image-guided Cardiac Catheter Ablation

Abstract

Accurate and fast fusion and display of real-time images of anatomy and associated data is critical for effective use in image guided procedures, including image guided cardiac catheter ablation. We have developed a piecewise patch-to-model matching method, a modification of the contractive projection point technique, for accurate and rapid matching between an intra-operative cardiac surface patch and a pre-operative cardiac surface model. Our method addresses the problems of fusing multimodality images and using non-rigid deformation between a surface patch and a surface model. A projection lookup table, K-nearest neighborhood search, and a final iteration of point-to-projection are used to reliably find the surface correspondence. Experimental results demonstrate that the method is fast, accurate and robust for real-time matching of intra-operative surface patches to pre-operative 3D surface models of the left atrium.

1. Introduction

Catheter-based ablation for treatment of cardiac arrhythmias has increased dramatically over the past decade [1–29]. In contrast to open chest surgical-based procedures, catheter-based ablation has significantly lower morbidity and mortality [8,9]. Because of the lack of direct visualization, the ablation procedure is accomplished via remote navigation of the catheter guided by real-time imaging and magnetically tracked catheters. Previous papers have reported using pre-operative image-based models of the left atrium to assist in guiding the procedure [10,11]. Since the pre-operative models computed from MR or CT images tend to be high resolution, large field-of-view (FOV) datasets, they are obtained before the procedure and, thus do not exactly represent the patient anatomy during the procedure. Real-time 3D imaging technologies, such as intra-cardiac ultrasound and rotational angiography, can be used to obtain volumetric datasets during an ablative procedure, but these datasets usually cover only a small FOV and/or are obtained at a lower resolution. In our approach, high-resolution pre-operative models are fused with real-time imaging datasets to enhance ease of navigation and accuracy of targeting in the procedure [12].

During an image-guided cardiac ablation procedure, a 3D map of the endocardial surface of the left atrium (LA) is created by sampling surface points from the LA using a magnetically tracked catheter. The 3D map, called an electro-anatomical map (EAM), is generated from 60 to 120 sampled points. Because the EAM is a low-resolution representation of the LA, several approaches have been developed to integrate a high-resolution pre-operative model of the LA [13–29]. Unfortunately, after the creation of the EAM and registration to the high-resolution model, the cardiologist will often return to x-ray fluoroscopy and/or intra-cardiac echocardiography for guidance because both provide real-time feedback of the anatomy and ablation catheter. In some cases, rotational angiography will also be used in obtaining a 3D dataset of the LA.

In order to improve the guidance and targeting of cardiac ablation, it is desirable to fuse the disparate datasets into a single representative model of the patient’s anatomy during the procedure. The fusion process should provide the most “up-to-date” display of the patient’s heart utilizing both the high-resolution pre-operative data and real-time image data. More specifically, as real-time 3D data is obtained (e.g., either through 3D ultrasound or rotational angiography), the data should be integrated into the high-resolution model to properly reflect the changes in the patient’s cardiac anatomy during the procedure. Fusion of these datasets, however, is not straightforward because the real-time data is lower-resolution than the pre-operative data and is obtained over a smaller FOV than the pre-operative data. In our approach, the intra-operative data (represented as a polygonal surface patch) is registered to the pre-operative model, which is represented as a closed polygonal surface. The intra-operative patch dynamically replaces the corresponding data in the high-resolution polygonal model.

2. Methods

In order to fuse the pre-operative surface model with the intra-operative image data, we must find the surface correspondence between them. Correspondence, in this case, requires both global and local alignment. While global alignment orients one datasets into the space of a second dataset, it does not provide the final mapping of one dataset to another due to local tissue deformation. As such, both global and local transformations must be considered. Global registration techniques have been previously validated and published. Global alignment can be achieved using a standard registration technique such as software-based registration [30] or landmark pair matching between pre-operative surface points [31,32] and intra-operative locations sampled by magnetically tracked US catheters [33]. In this work, we assume an initial global alignment has been computed using one of these standard techniques and we instead focus on refinement of an initial global registration. Because of the complex variation of the morphology of the LA during the cardiac cycle, the initial alignment is not acceptable as the final registration of the real-time data to the pre-operative model. However, with the surface patch coarsely aligned to the specific LA surface model, the vertices on the patch can serve as control points for acceptable refinement of the registration to the surface model.

There are three approaches widely used for refinement of 3D surface matching following initial alignment [34–37]: 1) point-to-point, e.g. iterative closest point (ICP) algorithm [38] and its variations, 2) point-to-(tangent-)plane [39], and 3) point-to-projection [40]. Unfortunately, the heavy computational burden of searching for the closest point on the destination surface negates the point-to-point and point-to-plane algorithms for real-time applications. The point-to-projection method is quite fast for registration refinement as it does not involve iterative searching steps to find the correspondence, but it is not as accurate as the other two methods because of the tradeoff between speed and accuracy. The contractive projection point (CPP) technique, developed by Park and Subbarao [34,41], provides a fast and accurate registration by combining the fast searching capability of the point-to-projection method and the most accurate performance of the point-to-plane method.

Although experimental results show that point-to-projection and CPP are promising techniques for refinement of 3D surface matching, they do not address the important issues of matching of multimodality, non-monotonic, and non-rigidly deformed surfaces with different sampling densities. These issues are present in many applications of medical imaging and other domains. Matching an intra-operative surface patch to a pre-operative surface model of the LA is such an application.

2.1 Point-to-projection method

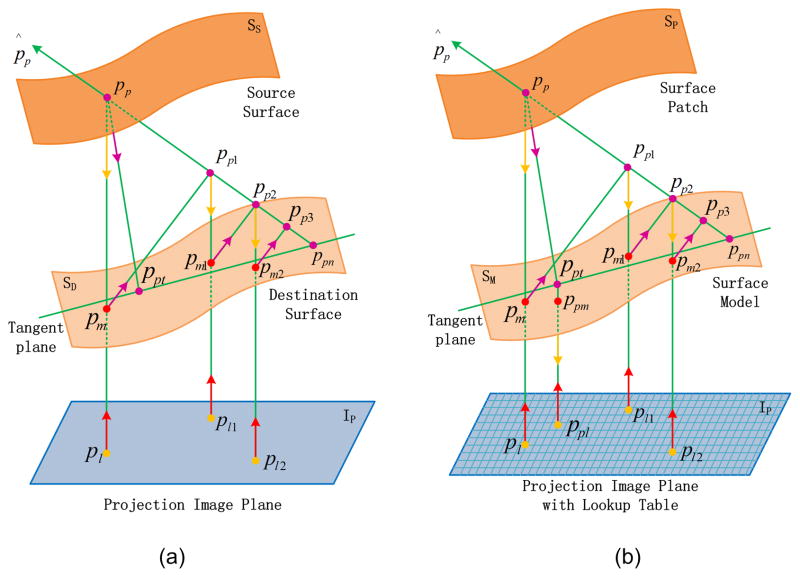
The point-to-projection method uses a projection ray to associate points on a source surface and a destination surface. As shown in Fig. 1(a), the 3D point p_p on the source surface is back-projected to a 2D point p_l on a certain image plane I_P according to the projection ray of the destination surface, and then the 2D point p_l is forward-projected to a 3D point p_m on the destination surface along the same projection ray. This method determines the point p_m on the destination surface as the corresponding point of point p_p on the source surface.

Fig. 1.

Finding the matching point between two surfaces, (a) point-to-projection method and CPP technique (adapted from [30]); (b) proposed patch-to-model method.

2.2 CPP technique

To achieve surface correspondence, the CPP technique utilizes an iterative point-to-projection approach to find the intersection on the destination surface corresponding to the point on the source surface, as illustrated in Fig. 1(a). Specifically,

1. The point-to-projection method is used to find the 3D point p_m on the destination surface, which is corresponding to the 3D point p_p on the source surface.

2. Instead of treating p_m as the final point on the destination surface for surface matching as the point-to-projection method does, p_m is projected to the normal vector p̂_p of p_p to get a new 3D point p_p1.

3. The point-to-projection on p_p is iterated on p_p1, p_p2, and so on, and p_m converges to 3D point p_pn on the destination surface.

4. p_p is projected again along the normal vector of p_pn to the tangent plane at p_pn, and the intersection p_pt is the final matching point on the destination surface corresponding to the source point p_p.

The point-to-projection and CPP techniques are limited for medical imaging applications for several reasons. First, in computing point p_m from point p_l, it is necessary to compute an interpolated grid on the projection image plane, and forward-project it to the world coordinate system. For traditional applications of point-to-projection and CPP (such as surface scanning data), this approach is feasible because the data is paired views or multi-views of a regularly sampled point cloud along a rectangular grid. It does not, however, work for an irregularly sampled point cloud of variable density as in the case of tiled medical imaging datasets. Second, the final matching point p_pt in the CPP technique is not guaranteed to match identically to the surface model, because that point is on the tangent plane but not on the surface model. Third, the point-to-projection method usually isn’t accurate enough for medical imaging applications. The proposed method addresses these three problems by setting up a projection lookup table for the surface patch and surface model separately, and projecting point p_pt to the surface model.

2.3 Proposed method

The proposed method determines the surface correspondence following initial alignment, including vertex matching and region matching, by projecting the surface patch to the surface model, as shown in Fig. 1(b). The detailed flow is as follows:

1. The projection axis and projection image plane for the surface patch and surface model are estimated according to the average patch normal and the center point of the surface model. In addition, the view point is estimated according to the center point of the surface patch, the projection axis and the projection image plane. With the estimated view point, projection axis and a certain view angle, the initial matching surface region can be defined in order to remove surface vertices and triangular tiles that are located outside of the desired matching surface region.

2. Two projection lookup tables, which maintain the correspondence between the 2D pixel on the projection image plane and the 3D vertex on the surface patch or surface model, are constructed separately by projecting all the vertices of the surface patch or the initial matching surface region to the projection image plane along the projection axis.

3. The CPP technique is used to find the vertex on the surface model corresponding to each vertex on the contour of the surface patch. The lookup table is used to find the vertex correspondence during each projection, instead of the direct forward-projection used in the original CPP technique.

4. The point p_pt, which is on the tangent plane of the convergent projection point p_pn, is projected once again to find the final vertex p_pm on the surface model, which corresponds to the vertex p_p on the surface patch.

5. The projection pixels of all the vertices on the surface model, corresponding to those on the contour of the surface patch, comprise a polygon on the image plane. The matching vertex set is composed of all the vertices on the surface model, whose projection pixels are located inside the polygon.

6. The entire matching region on the surface model is filled by the triangular tiles whose vertices all belong to the matching vertex set.

7. In the case of a “C-shaped” or closed cylindrical surface, the patch is divided into several sub-patches, and a piecewise matching method is used to obtain a complete matching region by combining the match results of all subpatches.

In the method described above, the modification proposed in this paper is applied to the CPP technique. By replacing the CPP technique with the point-to-projection method in step 3) and skipping the step 4), it is also applicable to the point-to-projection method. We apply our proposed modification to both the CPP and point-to-projection techniques and validate both methods in this paper.

3. Implementation

3.1 Estimation of projection axis and image plane

Unlike surface scanning data, the anatomic surface patch and surface model are derived from an unstructured point cloud or volumetric dataset. Accordingly, the projection axis and the projection image plane must be estimated before projecting the patch to the surface.

The projection axis n̂_p is estimated to be the vector of the average normal vector of the surface patch, as in equation 1 -

$${\widehat{n}}_p=\mathit{Normalize}(\sum _{i=0}^{n-1}{\widehat{n}}_{ti})$$ 1)

where n̂_ti is the normal vector of the ith tile of the n triangular tiles of the surface patch, and should always be the outward oriented normal.

The projection image plane is defined by a point on the plane and its normal vector, where the point is the center point of the bounding box of the surface model, and its normal vector is the vector of the projection axis. The view point p_v is estimated to be the projection point on the projection image plane, where the source point is the center point of the bounding box of the surface patch, as in equation 2 -

$$\begin{array}{l}d=(p_{mo}-p_{po})·{\widehat{n}}_p\\ p_v=p_{po}+{d\widehat{n}}_p\end{array}$$ 2)

where p_mo is the center point of the bounding box of the surface model, p_po is the center point of the bounding box of the patch, and d is the signed, shortest distance from p_po to the plane.

To remove surface vertices and triangular tiles that are located outside of the desired matching surface region, the initial matching region on the surface model, vertex set V_MI, is determined from the view point, projection axis and a given angle. The angle is defined between the vector of the projection axis and the vector from p_v to a vertex on the surface model, as in equation 3 -

$$V_{MI}=\left\{p_{mi}|\frac{(p_{mi}-p_v)·{\widehat{n}}_p}{\mid (p_{mi}-p_v)\mid }\ge cos(\pi /3),i=0,1,\cdots ,m-1\right\}$$ 3)

p_mi is the ith vertex of the m vertices on the surface model, and π/3 is the predefined angle to limit the initial matching region reasonably according to intra-operative surface patch.

3.2 Projection Lookup Table

The vertices on the surface patch and surface model are non-uniformly distributed and sampled with different point densities, so it is essential to set up a projection lookup table to maintain the correspondence between 3D vertices and 2D pixels on the image plane.

The projection image plane is divided into a grid to which the projection pixels are assigned. The pixel count in the projection contour of the initial matching region is determined by the vertex count of the initial matching region. To simplify the calculation, the bounding rectangle of the projection contour is used, and the vertex count, n_mv, is scaled by 1.5 (empirically determined) to ensure a significant coverage area. The dimension size of the projection rectangle on the image plane is given by equation 4 -

$$\begin{array}{l}{n}_x=\sqrt{1.5n_{mv}/r_{xy}}\\ n_y=r_{xy}{n}_x\end{array}$$ 4)

where r_xy is the ratio of height to width of the bounding rectangle, and n_x and n_y are the pixel count along the row and column of the bounding rectangle. If available, the original voxel size of the pre-operative volumetric dataset can alternatively be used to calculate n_x and n_y. With all the vertices of the initial matching region projected to the image plane, the multi-to–one mapping lookup table is established between the vertices of the initial matching region and the pixels on the image plane. The lookup table for the surface patch is also established with all the vertices of the surface patch projected to the projection image plane. With the two lookup tables, it is possible to find the vertex on the surface model corresponding to the vertex on the surface patch, which belongs to the same projection pixel during point-to-projection.

Because the vertices on the surface patch and surface model are not regularly sampled and distributed, it is not essential that the projection pixel, corresponding to the vertex on the surface patch, be directly mapped to one or more vertices on the surface model. Rather, the K-nearest neighborhood search method is used in the lookup table to find the nearest pixel, which has corresponding vertex on the surface model mapped to the same projection pixel. To ensure robust performance, the K value is iterated from 1, 8, 24, 48 to 80, and the search is from top to bottom and from left to right during each iteration. The projection pixel is rejected if a valid nearest pixel could not be found during the complete iteration.

3.3 Matching region filling

To decrease the dependence on the point cloud density of the patch and to meet the real-time requirement, only vertices on the 3D contour of the surface patch are projected to the surface model, and the matching region is filled according to the corresponding vertices on the surface model.

The closed contour of the surface patch is extracted based on the connectivity information from the triangle tiles. With all the vertices of the contour of the surface patch projected to the image plane, the nearest pixels found in the lookup table can be connected in the same order as the contour to form a polygon on the image plane. Due to the irregular geometry of the anatomy, the polygon generally is complex because it is projected from a 3D contour to a 2D image plane. The projected 2D polygon may have holes and isolated regions. To address this, the complex polygon is converted to a simple form before filling the matching region. All the vertices of the complex polygon are sorted radially around the center point of the bounding rectangle of the polygon, and they are connected in the sorted order to form a simple polygon.

Using the simple polygon and the lookup table, the set of vertices on the surface model can be determined, with a projection pixel located on the polygon or inside the polygon. The matching region is filled with all the triangle tiles of the surface model that belong to the vertex set.

3.4 Piecewise matching

To estimate the projection axis, the average patch normal is used. However, the average patch normal may not represent the projection axis when the patch is significantly curved, for example, if the intra-operative patch for the LA is a C-shaped or closed cylindrical surface. Therefore, the patch is divided into sub-patches to make the projection axis feasible. In sub-dividing the patch, adjacent regions are padded to ensure overlap between sub-patches. Each of the sub-patches is projected to the surface model to get the corresponding matched sub-regions, and finally they are combined into a complete matching region.

4. Results

A detailed validation protocol was designed to validate the capabilities of the proposed method using a real patient LA surface model. The method was also evaluated with a simulated surface model constructed from a physical phantom and two real LA surface models, which were generated from a single patient obtained at different points in the cardiac cycle.

4.1 Validation

The proposed modification was applied to both the point-to-projection and CPP techniques, and the capabilities and accuracy of both the modified methods were evaluated. As previously mentioned, the modified method using point-to-projection method has better time performance because there is no iterative projection in finding matching points. However, more accurate matching results are obtained by the modified method using CPP technique, with a minimal increase in computation time.

The validation dataset consisted of a LA pre-operative CT volumetric dataset. A surface model was extracted from the CT volumetric dataset, and the surface patch was simulated from the surface model with a region growing method. The surface patch was grown from a user-defined seed point on the surface model for 15 iterations, and the triangular tiles connected to the current surface patch were merged into the patch during each iteration. Therefore, the region on the surface model corresponding to the simulated surface patch is the theoretic matched region, and the vertices on the contour of the surface patch and their corresponding vertices on the surface model are two ground truth vertex sets, as illustrated in Fig. 2.

Fig. 2.

Surface model and surface patch (colored in red) for validation. The surface model was extracted from a CT volumetric data of a real patient, and the surface patch was simulated from the surface model with a region growing method.

The validation protocol was carried out by performing a transformation on the surface patch to simulate the translation, rotation, expansion and contraction behavior of the intra-operative LA. The surface patch and surface model were translated with p_mo translated to the origin of the world coordinate system initially, then rotated with p_mo fixed at the origin to make the vector n̂_p to be the axis Z in the world coordinate system. The transform matrix includes translation along Axis X, Y and Z, rotation with Axis X, Y and Z and scale, with random combinations of these rigid transformations. Specifically, the validation protocol was as follows:

1. The surface patch is translated along Axis X, Y, and Z from the initial position between −5mm to 5mm with step of 0.1mm, separately.

2. The surface patch is rotated separately with Axis X, Y, and Z from the initial position between −25° to 25° with step of 0.5°.

3. The surface patch is scaled from 80% to 120% with step of 0.4%, separately.

4. The surface patch is transformed with random combinations of translation along Axis X, Y, and Z between −2.5mm to 2.5mm, rotation with Axis X, Y, and Z between −10° and 10°, and scale between 90% and 110%.

The validation results were sorted and compared based on the average distance D_ad between the two ground truth vertex sets, as shown in equation 5 -

$$D_{ad}=\frac{1}{n_{vc}}\sum _{i=0}^{n_{vc}-1}\mid p_{\mathit{vci}}-p_{\mathit{vmi}}\mid$$ 5)

where n_vc is the vertex count on the contour of the surface patch; p_vci is the vector of the ith vertex on the contour of the surface patch; and p_vmi is the vector of vertex on the surface model corresponding to p_vci.

The area matching ratio of the matched region R_am is calculated based on the positive matched area, A_pm, the negative matched area, A_fm, and the false positive matched area, A_fpm, of the matched region, as shown in equation 6 -

$$\begin{array}{l}{R}_{am}=A_{pm}/(A_{tp}+A_{\mathit{fpm}})\\ A_{tp}=A_{pm}+A_{fm}\end{array}$$ 6)

where A_tp is the area of the theoretic matched region, i.e., the area of the surface patch. Each area is a summary of the area of the triangular tiles belonging to that region.

The average distance D_adm between the contour vertex of the matched region and the theoretic matched region is also measured and compared, as in equation 7 -

$$D_{\mathit{adm}}=\frac{1}{n_{vc}}\sum _{i=0}^{n_{vc}-1}\mid p_{\mathit{vmmi}}-p_{\mathit{vmi}}\mid$$ 7)

where p_vmmi is the vector of the mached vertex on the surface model corresponding to p_vci.

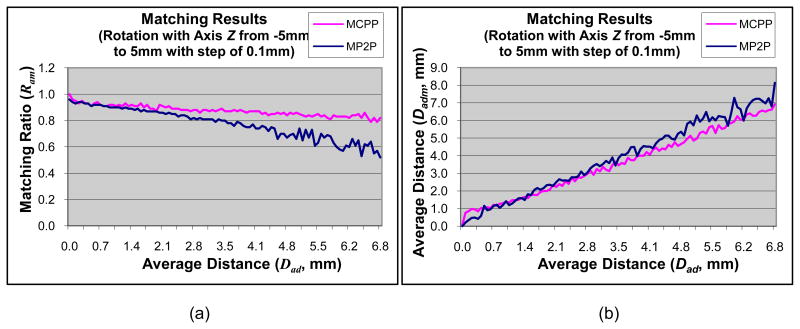
The matching results of translation along the x-axis are shown in Fig. 3. The results for translation along the y-axis are similar to the x-axis data. The matching results using the modified CPP technique and the modified point-to-projection method are very similar. The modified CPP technique, however, has better performance in terms of a higher matching ratio, a smaller average distance D_adm, and more stable results. The matching results of translation along Axis Z are shown in Fig. 4. The test data is oriented largely along the z-axis; therefore, the matching metrics of ratios and average distances are higher for translations along the z-axis. The matching results of rotation around the z-axis are shown in Fig. 5. The results for x- and y-axis are comparable. The modified CPP technique demonstrates better performance than the modified point-to-projection method, most likely due to the iterative convergent nature of CPP technique and the proposed final iteration of point-to-projection. The matching results of scale are shown in Fig. 6. Both methods yield comparable results.

Fig. 3.

Matching results of translation along Axis X between modified CPP (MCPP, pink line) and modified point-to-projection (MP2P, blue line). (a) Matching ratio of matched region; (b) Average distance of matched region.

Fig. 4.

Matching results of translation along Axis Z between modified CPP (MCPP, pink line) and modified point-to-projection (MP2P, blue line). (a) Matching ratio of matched region; (b) Average distance of matched region.

Fig. 5.

Matching results of rotation with Axis Z between modified CPP (MCPP, pink line) and modified point-to-projection (MP2P, blue line). (a) Matching ratio of matched region; (b) Average distance of matched region.

Fig. 6.

Matching results of scale between modified CPP (MCPP, pink line) and modified point-to-projection (MP2P, blue line). (a) Matching ratio of matched region; (b) Average distance of matched region.

The matching results for random transformations are shown in Fig. 7. The final matrix of random transformations is a not a full affine transformation. Instead, it consists of 3 translation, 3 rotations, and a single scale. The matching results show that the modified CPP technique has better performance than the modified point-to-projection method. In order to summarize the data, the absolute difference between D_adm and D_ad is computed. The mean and standard deviation of absolute difference is −0.65 mm +/− 1.31 for the proposed method using the modified CPP technique and −0.49 mm +/− 3.05 for the modified point-to-projection method. This suggests that the modified CPP technique yields a more consistent and stable result than the modified point-to-projection method.

Fig. 7.

Matching results of random transformation between modified CPP (MCPP, pink line) and modified point-to-projection (MP2P, blue line). (a) Matching ratio of matched region; (b) Average distance of matched region.

All validation experiments were carried out using C/C++ software developed in our lab that runs on Microsoft® Windows® XP with Service Pack 3. The PC’s configuration is Intel® Pentium® 4 3.20 GHz core duo CPU with 2 GB RAM. The vertex count of the surface model was 25,299 and the triangular tile count of the surface model was 50,840. The vertex count of the surface patch was 1,149 and the triangular tile count of the surface patch was 1,925. The modified point-to-projection method required 60–90 ms to compute, and the modified CPP method required 150–250 ms to compute. The modified point-to-projection method is faster than the modified CPP method because the former has only one projection and the latter has 6 projections during the matching process. The modified CPP technique, however, is more accurate and robust while still performing very rapidly.

4.2 Evaluation

Given the results of the validation experiments, our proposed method using the CPP technique provides better accuracy with acceptable real-time performance. Therefore, we have adopted the modified CPP algorithm as our preferred patch-to-surface technique and evaluated this proposed method in two image-guidance applications. The first experiment utilizes a simulated surface model constructed from a physical phantom imaged with real-time ultrasound. The second experiment utilizes two LA surface models generated from a patient, multi-phase CT volumetric dataset at two points in the cardiac cycle. The physical phantom is a simple 2-chamber phantom, as illustrated in Fig. 8(a). A 3D volumetric dataset of the model was generated based on the measured orthogonal dimensions of the model. The volumetric model was segmented and tiled. Fig. 8(b) and 8(c) show the epicardial and endocardial surfaces, respectively.

Fig8.

Physical phantom, (a) Photo view; (b) Epicardial surface view; (c) Endocardial surface view.

To evaluate the process of matching the intra-operative surface patch to a pre-operative surface model with the physical phantom, several intra-operative US images of the LA components were collected (Fig. 9(a)). Using a standard image registration algorithm, a single US image was registered to the synthetic volume data (Fig. 9(b)). The contour of the LA section, Fig. 9(c), was segmented from the US images and duplicated 10 times to generate synthetic 3D data. The 3D patch was tiled to generate the intra-operative surface patch of the LA, Fig. 9(d). Due to small segmentation and registration error, there is some space between the surface patch and surface model, as shown in Fig. 9(e). Using our method, the surface patch was projected to the surface model. Fig. 9(f) shows the correspondence between the surface patch (purple) and the matched region extracted from the surface model (red), with part of the top-right region zoomed in the bottom-right area. The matched region of the surface model was removed yielding a fused model and patch (fig. 9(g)). Visual inspection confirms that the expected surface correspondence is achieved by projecting the surface patch to the surface model using the new method.

Fig 9.

Patch and surface dataset of physical phantom, (a) Intra-operative US image of LA section; (b) Image correlation between LA template and US image of LA section; (c) Endocardial contour of LA section; (d) Endocardial patch of LA; (e) Initial registration of endocardial patch and surface of LA; (f) Endocardial patch and matched region with part of the top-right region zoomed in the bottom-right area; (g) Original endocardial patch and surface with matched region removed.

In addition, the proposed method was also tested with a simulated pre-operative surface and intra-operative patch. To generate the data used in this study, two datasets were taken from a multi-phase CT scan of a single patient. As expected, due to the change of the LA through the cardiac cycle the segmentations are similar although not exactly corresponding. The first scan is polygonalized into a high-resolution surface model (Fig. 10(a)). The second scan is also polygonalized to generate a surface patch representative of segmented intra-operative US data (Fig. 10(b)). The simulated intra-operative surface patch was projected to the pre-operative surface model (Fig. 10(c)). Fig. 10(d) shows the final result with the original data removed and replaced with the patch. In this case, the matching region represents the simulation of elastic deformation of the surface patch. When the surface patch is transformed to the outside of the surface model, the matching region contracts to a smaller region than the theoretical matching region, which simulates the intra-operative expansion/contraction of the LA.

Fig 10.

Mapping a LA surface patch to a LA surface model, (a) The high resolution pre-operative surface model; (b) The surface model with the surface patch from simulated intra-operative data; (c) The surface model with matching region projected from the surface patch; (d) The surface model with all of the projected points removed from the model and the surface patch.

5. Discussion

Our new algorithm successfully addresses several pitfalls encountered in previous methods. Specifically, our method accommodates real-time, dynamic geometry that may be somewhat different from the pre-operative model. The piecewise patch-to-model method also allows the two datasets to initially be marginally out of alignment while still achieving adequate alignment. Moreover, the two datasets are not required to be sampled at the same resolution. To ensure that the algorithm is robust, several simulation phantom studies were conducted which verified that the method accurately matched the patch to the model, even with 5mm disparity from the original orientation. In addition to being robust, the method must be fast so that it can be utilized several times during an image-guidance procedure. Generally speaking, intra-operative volumetric datasets are acquired over 10–60 seconds. Accordingly, the time to fuse the intra-operative data into the model must meet this time constraint. The proposed method is very efficient and meets this requirement. During the validation study, the modified CPP technique was similar to the modified point-to-projection method with regards to the performance metrics. This is not surprising as the dataset used in the validation study contained both the surface model and the patch. Accordingly, the modified point-to-projection method is well-suited to directly align the two surfaces. It is expected that the modified CPP method will be very robust under realistic conditions and is therefore our preferred patch-to-model method for image guidance applications.

In the context of cardiac ablation, there are two generally recognized intra-operative volumetric imaging datasets which may be obtained. Intra-cardiac or trans-esophogeal echo can be used to reconstruct a 3D US dataset [42,43] which in turn can be used to generate a surface model of a portion of the left atrium. Rotational angiography can be used to obtain a volumetric dataset spanning most of the anatomic extent of the heart during a procedure. Image-guided cardiac ablation requires the fusion of these on-line datasets with high-resolution, large FOV pre-operative datasets [6,11,44]. Pre-operative data is acquired 24–48 hours prior to the procedure and does not accurately represent the cardiac morphology at the time of the procedure. Real-time processing algorithms must be used to fuse these datasets during the procedure. As part of the fusion process, the pre-operative data must be replaced with the intra-operative data while maintaining the integrity of the dynamic visualized results. Our proposed piecewise patch-to-model algorithm accomplishes this task by projecting the real-time data onto the pre-operative model and replacing the corresponding patch in new real time.

Pre-operative CT to intra-operative US is one of the primary applications of this technology. In order to validate our technique, we tested the approach using simulated and phantom datasets. Specifically, selecting two time-points of a multi-phase CT ensured that we were evaluating the local alignment problem rather than the global registration problem (see Fig. 9). We also believe that validation experiments using a phantom surface generated from real-time US images and the surface generated from its associated CT volume data have demonstrated the scientific validity of this technique and its potential for future clinical use (as shown in Fig. 10).

This approach may be utilized in other image guidance procedures. For example, in the case of laparoscopic or endoscopic procedures, a pre-operative model can be generated from high-resolution MR or CT and serve as the basis for image-guidance during the procedure. As surface data is obtained from the laparoscope, it can be fused with the pre-operative model. Another application would be to correctly represent the deformation of a pre-operative MR brain dataset in neuro-surgery. In this case, either surface range data or intra-operative US can be used to obtain real-time surface patches of data [45]. Future studies will apply the patch-to-model algorithm to these other real-time procedures.

Biographies

Jiquan Liu received his PhD in biomedical engineering from Zhejiang University, China. Currently he is working in Zhejiang University as an associated research fellow, and doing collaborative research in Biomedical Imaging Resource Laboratory at Mayo Clinic as a postdoctoral research fellow. His research interests include medical image processing, visualization, and image-guided surgery.

Maryam E. Rettmann received her PhD in biomedical engineering from the Johns Hopkins University. She has held post-doctoral positions in the National Institute on Aging at the National Institutes of Health and in the Department of Physiology and Biomedical Engineering at Mayo Clinic. She is currently an Assistant Professor of Biomedical Engineering in the Mayo Graduate School at Mayo Clinic, Rochester, MN. Her research interests include medical image analysis and image-guided interventions.

David R. Holmes III received his degree from the Mayo Graduate School at Mayo Clinic, Rochester, MN. David is a researcher and core director in the Biomedical Imaging Resource. His research interests include image analysis and image guidance. He is involved with image guidance research on the heart, brain, and prostate.

Huilong Duan received his B.S. in Medical Instrumentation from Zhejiang University, China in 1985, M.S. in Biomedical Engineering from Zhejiang University, China in 1988, and Ph.D. in Engineering (Evoked Potential) from Zhejiang University, China in 1991. He is currently a Professor in the Department of Biomedical Engineering, and the Dean of College of Biomedical Engineering & Instrument Science, Zhejiang University. His research interests are in Medical Image Processing, Medical Information System and Biomedical Informatics. He has published over 90 scholarly research papers in the above research areas. He is Program Committee Member of Computer Aided Radiology and Surgery; Reviewer and Editorial Board of Space Medicine & Medical Engineering and Chinese Journal of Medical Instruments respectively; Reviewer of Journal of Image and Graphics; Editorial Board of Chinese Journal of Biomedical Engineering; Secretary-General of BME Education Steering Committee, Chinese Ministry of Education; Member of the Brain-Bridge Program Committee, Philips, TU/e & ZJU.

Dr. Richard A. Robb is Professor of Biophysics and Professor of Computer Science in Mayo Medical School, Mayo Graduate School and the Department of Physiology and Biomedical Engineering at Mayo Clinic. He also holds a named professorship–The Scheller Professorship in Medical Research–that endows his research and educational activities. He is Director of the Biomedical Imaging Resource Research Laboratory at Mayo Clinic. He has a long and productive career of over 35 years in biomedical imaging science research and translation to clinical applications with experience in all aspects of biomedical imaging, ranging from acquisition through analysis to application. He has been funded over that time primarily by NIH grants, but also by philanthropic foundations and industrial sponsors. He has over 400 publications in the field, including 5 books and 30 book chapters and holds several patents related to inventions in multi-dimensional image display, manipulation and analysis. Software systems developed in his laboratory have been disseminated to over 500 institutions around the world. His current research interests are in development of modular image analysis software systems for advanced diagnosis and treatment, and in development and validation of real-time image-guided medical interventions.