Kinetochores’ Gripping Feat: Conformational Wave or Biased Diffusion?

Abstract

Climbing up a cliff while the rope unravels underneath your fingers does not sound like a well planned adventure. Yet chromosomes face a similar challenge during each cell division. Their alignment and accurate segregation depends on staying attached to the assembling and disassembling tips of microtubule fibers. This coupling is mediated by kinetochores, intricate machines that attach chromosomes to an ever changing microtubule substrate. Two models for kinetochore-microtubule coupling were proposed a quarter century ago: conformational wave and biased diffusion. These two models differ in their predictions for how coupling is performed and therefore in how the coupling can be regulated. The availability of purified kinetochore proteins has enabled a series of biochemical and biophysical analyses of the kinetochore-microtubule interface. Here, we discuss what these studies reveal about the contributions of each model.

Dynamic microtubules drive mitosis

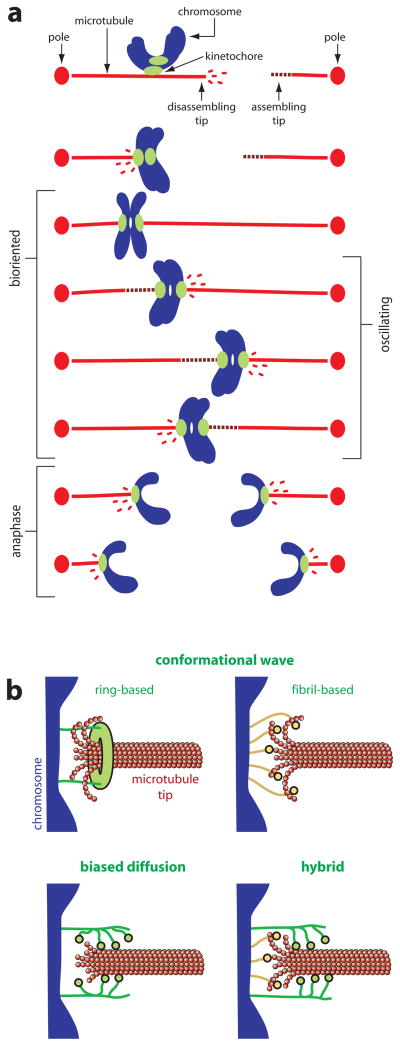
During cell division, duplicated chromosomes are accurately distributed to each daughter cell by the mitotic spindle, a microtubule-based molecular machine. Microtubules are protein polymers, composed of thousands of tubulin dimers arranged as a miniature tube. Microtubules in the spindle constantly grow and shorten by addition and loss of tubulin dimers from their tips. Chromosomes attach to microtubules through specialized multiprotein organelles called kinetochores. Remarkably, the kinetochores maintain attachments to microtubule tips even as the tips assemble and disassemble. This enables kinetochores to couple chromosome movement to the growth and shortening of microtubules (Fig. Ia). Tubulin is an enzyme, a GTPase, which implies that microtubules are molecular machines in their own right, with capacity to do work. By remaining coupled to disassembling tips, kinetochores harness microtubule shortening to generate pulling force (Fig. Ia). While the level of force at kinetochore-microtubule junctions in vivo is not fully resolved (see below), it is substantially above the femtoNewtons required to simply move chromosomes through cytoplasm. How kinetochores achieve this strong yet dynamic coupling to the microtubule tip is still a mystery.

Figure I. Chromosome-microtubule coupling during mitosis.

(a) Chromosome movement during mitosis is coupled to the growth and shortening of microtubule tips. Each duplicated chromosome has two kinetochores, one on each sister chromatid, through which they attach to the microtubules of the mitotic spindle. Initially, the kinetochores make lateral attachments to the sides of microtubules, but these attachments are converted to an end-on arrangement and thereafter the kinetochores remain persistently associated with the assembling and disassembling microtubule tips. The linkages between kinetochores and disassembling tips are sites where pulling force, directed toward the poles, is generated (i.e., these are sites where chemical energy is converted into mechanical work). When a chromosome becomes properly bioriented – with one kinetochore attached to the left side of the spindle and the other attached to the right side – pulling forces generated on one side are resisted by the connections on the other side. These opposing forces place bioriented sister kinetochores under tension, which stretches them apart from one another. In some types of cells, bioriented chromosomes oscillate back-and-forth around the spindle equator, making movements that are coupled to alternating cycles of growth and shortening of the opposing microtubules. In anaphase, after cohesion between sister chromatids is dissolved, microtubules on both sides of the spindle disassemble, thereby pulling the sisters toward opposite poles. (b) Models for chromosome-microtubule coupling. Two versions of the conformational wave mechanism are shown, one (ring-based) in which elements of the kinetochore assemble into a microtubule-encircling ring that is hooked by curling protofilaments, and another (fibril-based) where fibrillar kinetochore elements bind independently to the curling protofilaments. In either case, the curling action of the protofilaments exerts pulling force (directed rightward in the diagrams) on the chromosome. In the biased diffusion mechanism, an array of kinetochore fibers rapidly binds and unbinds the microtubule lattice at or near the tip. Thermal fluctuations of the chromosome that allow more fibers to bind (rightward movements of the chromosome in the diagram) are favored by the energy of binding those elements. This biased thermal movement produces a thermodynamic pulling force. A hybrid model is also shown, where force is produced by a combination of protofilament curling and biased thermal fluctuations.

Models describing kinetochore-microtubule coupling were proposed before the kinetochore proteins were identified, thus definitive tests of these models were difficult to perform. In the last few years, the proteins that constitute the core of the budding yeast (Saccharomyces cerevisiae) kinetochore were identified and many are conserved in humans [1, 2]. The discovery that small groups of these proteins form stable complexes that can be produced in significant amounts in recombinant form [3–6] opens the door to uncover how kinetochores grip dynamic microtubules.

Models for kinetochore-microtubule coupling

Three types of models have been proposed to explain how kinetochores attach chromosomes to disassembling microtubule tips. One idea is that ATP-powered motor proteins attach kinetochores to the ends of microtubules. Although motors play critical roles in mitosis, their deletion or depletion does not detach the chromosomes from the spindle [1, 7–10], so they are unlikely to form the primary attachment.

Two classes of models remain under consideration, conformational wave and biased diffusion [11, 12]. In the conformational wave model (Fig. Ib) kinetochore movement is driven by large conformational changes, or ‘power strokes’, occurring at the microtubule tip [11]. The energy for these strokes comes from bending strain trapped in the microtubule lattice (which in turn comes from hydrolysis of GTP by tubulin). The strain is released during disassembly when individual columns of tubulin subunits, called protofilaments, curl outward from the lattice [13]. In the conformational wave model, these curling protofilaments pull continuously on the kinetochore. Theoretical considerations suggest that this mechanism can produce movement and force [14] (Box 1). If the coupler has significant affinity for the microtubule lattice, then the peeling protofilaments may also need to overcome a frictional resistance to drive movement as proposed in the ‘forced walk’ model [15].

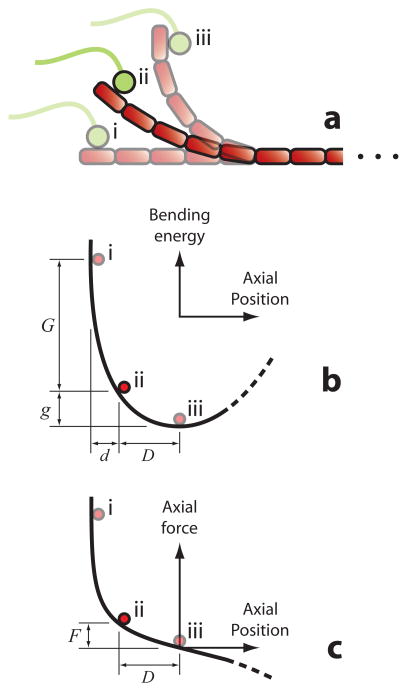
Box 1. Physics underlying the conformational wave.

In the conformational wave model, curling protofilaments at disassembling tips exert pulling forces on the kinetochore. To understand the physics behind this mechanism, it is helpful to consider the bending energy and movement of a single protofilament as it curls away from the microtubule lattice (Fig. II).

The energy is initially high because a straight protofilament (Fig. II, conformation i) is far from its naturally curved shape (Fig. II, conformation iii). At first, the curling movement is mainly directed radially outward from the microtubule lattice (upward in Fig. IIa), which is unproductive. As a consequence, much energy is lost before a useful power stroke can occur. Productive movement (i.e., longitudinal, rightward in Figs. IIa, IIb, and IIc) occurs only after a significant angle develops between the protofilament and the microtubule axis, so the efficacy of the mechanism depends on the extent of curling that occurs before the protofilament breaks. (In this respect it is similar to biased diffusion – both are essentially races against disassembly.) Theoretical treatments often assume that large curls always develop [14, 15, 37, 62]. However, observations in vivo suggest that only half of the protofilaments develop large curls (6 of 13 on average [36]). Likewise, the extent of curling in vitro varies widely depending on experimental conditions [13]. The most productive curls will be those ~5 tubulin dimers in length or longer, corresponding to angles ≥ 90° [13, 36] and longitudinal movements of ≥ 15 nm.

To provide a useful power stroke, the curls must also be stiff enough to resist bending under the load force of the kinetochore. A compliant protofilament would be like a flimsy kayak paddle – ineffective. Estimates of the flexural rigidity of individual protofilaments span a 9-fold range, from EI = 1,500 to 13,000 pN nm² (corresponding to energies of 3.7 to 32 k_BT per dimer for full straightening) [14, 63–66]. If their actual rigidity is near the top of this range, then their stiffness is easily sufficient to provide an effective power stroke. However, if their actual flexural rigidity is nearer the bottom of the range, then the curls will be fairly compliant. As an example, a 5-dimer curl with flexural rigidity EI = 1,500 pN nm² would be soft enough that just 1 pN of load would reduce its power stroke to half the unloaded distance. Higher loads could virtually eliminate the stroke. (The stiffness for modest deflections, k = 0.11 pN nm⁻¹, can be calculated by considering the protofilament as a semi-circular cantilevered beam [67].)

An alternative view is the biased diffusion model (Fig. Ib), first proposed by Hill [12], in which the kinetochore consists of multiple elements that form diffusive attachments to the microtubule. As these attachments diffuse along the filament, any motion of the kinetochore that brings more of its binding elements within range of the lattice is favored by the energy of binding those elements to the microtubule. Put differently, Brownian motion onto the microtubule tip is favored over Brownian motion away from the tip (Box 2). Hill showed theoretically that biased diffusion-based couplers can remain persistently attached to disassembling microtubule tips and withstand external forces opposite the direction of disassembly (i.e., they can perform mechanical work).

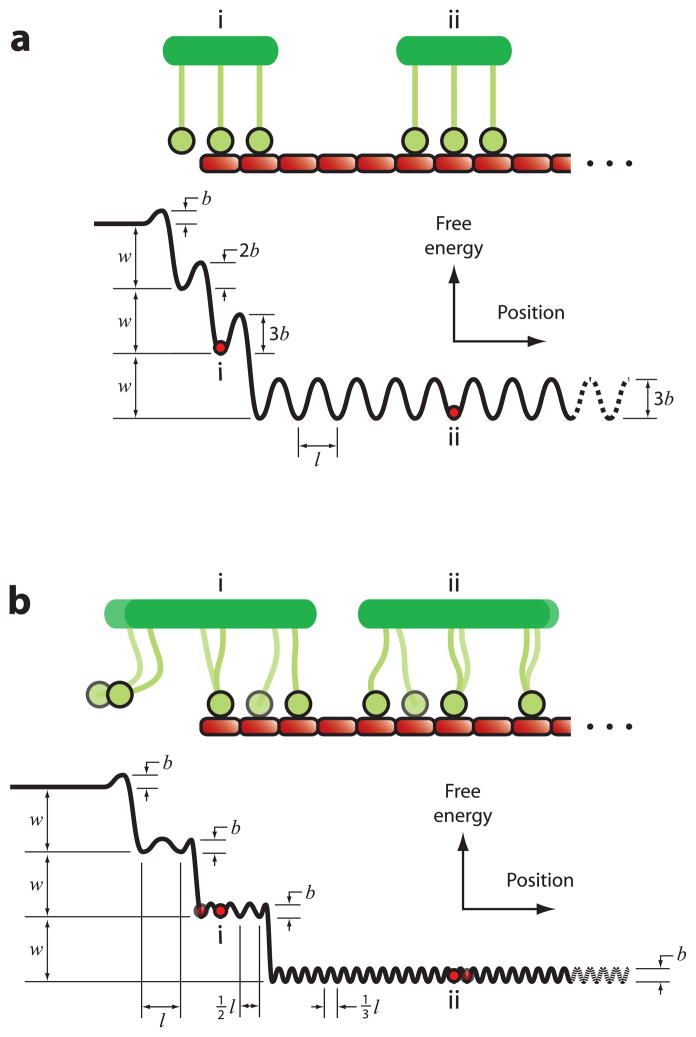
Box 2. Physics underlying biased diffusion.

In the biased diffusion model, the kinetochore contains an array of individually weak binding elements that bind and unbind rapidly from the microtubule lattice. Hill [12] showed theoretically that such an array will track persistently with a disassembling tip, even under tension, provided its diffusion is fast enough and its total binding energy is large enough.

The physics behind biased diffusion is best understood by considering how free energy varies with the position of the array on the microtubule lattice (Fig. III). When bound far from the tip (position ii), moving the array to a nearby location will require breaking some bonds, but this energy is quickly regained as the bonds re-form at new sites. Thus the energy landscape in this region is corrugated but essentially flat, which leads (in the absence of external force) to unbiased, thermally-driven diffusion at a rate that depends on the corrugation height and step size. If the coupler begins to move off the tip (position i) its free energy increases because some binding elements can no longer reach the filament. This energy gradient biases the thermal fluctuations, favoring movement back onto the filament (rightward in Fig. III). Equivalently, it produces a thermodynamic force that pulls the array back onto the filament, even against an opposing load. A microtubule tip is not strictly necessary for biased diffusion, since the required energy gradient could arise instead from a boundary between different types of tubulin dimers near the tip. For example, it could occur at the transition from straight to curved tubulin dimers. Regardless of the exact position of the energy gradient, however, tip tracking requires the diffusion of the tip-associated coupler to be fast enough and biased enough to outrun disassembly.

The shape of the energy landscape, and thus the tracking performance of the array, will depend on details such as the number and flexibility of the individual elements. Hill [12] considered the simplest one-dimensional scenario, with a rigid array of binding elements whose spacing matched the microtubule lattice (similar to Fig. IIIa). While he imagined them arranged as a tight-fitting ‘sleeve’ encircling the microtubule, the physical underpinnings of his model apply far more generally, even to a flexible, disordered array of binding elements. Flexibility within the array would be advantageous because the height of the corrugations and the effective step size will be reduced if the binding elements move independently of one another (as shown schematically in Fig. IIIb). Reducing the step size may increase the maximum force that the mechanism can produce, which is set by the slope of the steepest portion of the energy landscape. The rate of diffusion is predicted to increase locally near the tip, either because the corrugation heights are lower near the tip (as in Fig. IIIa), or because the effective step size is larger (as in Fig. IIIb). This local increase in diffusion rate means that the couplers do not need to diffuse rapidly when they are bound far from the tip. Indeed, couplers with large numbers of elements that are nearly immobile when bound far from the tip can still track effectively with disassembling tips because when they become tip-associated, fewer elements remain attached and their diffusion rate increases [46].

Forces generated by power strokes and by biased diffusion are known in other cytoskeletal systems [16]. Muscle contraction is driven by a large conformational change (a power stroke), rotation of the lever arm of myosin [17]. By contrast, biased diffusion (also called a Brownian ratchet) explains how actin filaments push against membranes at the leading edges of crawling cells [18, 19], and how microtubules push against the cortex in fission yeast [20, 21]. It is important to note that power strokes and biased diffusion are not mutually exclusive [16]. In fact, processive kinesins and non-muscle myosins likely exploit both to effect movement (e.g., see [22, 23]). In these cases, conformational changes induced by nucleotide hydrolysis (or product release) are responsible for only part of the movement—the remainder comes from biased diffusion.

Regulation of kinetochore-microtubule attachment is essential for achieving correct bioriented attachments [24, 25]. The conformational wave and biased diffusion mechanisms imply different strategies for this regulation. For example, if kinetochore-microtubule coupling occurs by the conformational wave mechanism, then one likely target for regulation would be the affinity of kinetochore components for curled protofilaments. Another target could be the lengths of the curls, or the overall shape of the microtubule tip, which might be modulated by various kinetochore or non-kinetochore tip-binding proteins [26, 27]. On the other hand, if the biased diffusion model is correct, then regulation could occur by modulation of the rates of lattice diffusion, or lattice binding and unbinding, of kinetochore components.

So in the spectrum between conformational wave and biased diffusion, where does the kinetochore stand? Here we summarize recent findings, from experiments in vitro and in vivo, and from theoretical and computational studies, with emphasis on how the observations relate to the mechanism of kinetochore-microtubule coupling.

The case for conformational wave

In vitro, microtubules disassemble in a two-step process. The protofilaments first peel away from the tip of the filament, and then they break apart into curled fragments [13, 28]. This observation, first made over 25 years ago by electron microscopy, led naturally to the hypothesis that protofilament curling might be harnessed to drive kinetochore movement [11]. The idea appeals to our aesthetic sense of what seems like a robust coupling mechanism. But our intuition is based on familiarity with everyday objects (e.g., simple machines such as pulleys or levers). Does it apply to kinetochores?

New enthusiasm for the conformational wave idea came from the recent discovery that Dam1, a ten-protein complex from the kinetochores of budding yeast, when purified and mixed with pure microtubules in vitro, spontaneously assembles into rings around the microtubules [3, 6]. These microtubule-encircling rings may be the perfect mediators of a conformational wave mechanism because, theoretically, any protofilament that peels out far enough from the microtubule tip could hook the ring and tug on it [29]. Enthusiasm grew further when experiments showed that fluorescent-tagged Dam1 complexes [30] and Dam1-decorated beads [31] track processively with disassembling tips in vitro. However, the number of complexes required for tracking in vitro (in the absence of tensile load) was later found to be fewer than the sixteen needed to form a ring [32, 33]. The same result was obtained in vivo with the Dam1 complex from fission yeast (Schizosaccharomyces pombe) [34]. So rings are not strictly required for disassembly-driven movement of the Dam1 complex.

The functional significance of Dam1 rings will remain uncertain until the structure of the kinetochore is known. But even if it were known whether rings existed in vivo, this knowledge would not resolve our central question, which is fundamentally about mechanism, not structure. For example, if rings do exist in vivo they could act primarily via biased diffusion rather than through a conformational wave mechanism. In fact, a ring or sleeve might be ideal for coupling via biased diffusion, since this arrangement could provide many potential interactions between the coupler and the filament (e.g., see discussion in [35]). Conversely, if rings are absent in vivo the conformational wave mechanism will not be ruled out, since kinetochore-anchored fibrils, rather than rings, could harness protofilament curling to drive movement and force production [36]. Thus the structural question, “are rings functionally significant for kinetochore-microtubule coupling?” must be considered independently from the mechanistic question, “is kinetochore movement driven by a conformational wave, by biased diffusion, or by both?”

Despite the uncertainties regarding Dam1 rings, the conformational wave mechanism remains an attractive possibility. Several other in vitro experiments provide suggestive, but not definitive evidence for the idea. Disassembling microtubule tips exert brief pulses of force, 0.24 pN and lasting 1.3 s, that drive small displacements (~30 nm) of beads attached via tight biotin-avidin linkages [37]. (Extrapolating from this measurement, the authors suggested that under optimal conditions a disassembling microtubule could exert 30 to 65 pN, but such high forces have never been directly measured.) These transient pulses suggest that the curling of one or more protofilaments can exert a brief tugging force. However, whether they can pull continuously, like a kinetochore-attached tip in vivo, remains uncertain. Continuous tension can be generated by more processive tip attachments, such as those composed of Dam1 complex alone [38], combinations of Ndc80 and Dam1 complexes [39] (Box 3), or native kinetochore particles purified from budding yeast (Akiyoshi et al., unpublished results [40]). Tension applied through these processive couplers inhibits disassembly of the microtubule [38–40]. The most straightforward interpretation is that some load is transmitted to the outwardly curling protofilaments, tending to straighten them. This would imply (by Newton’s third law) that the curling protofilaments exert an equal and opposite force on the coupler.

Box 3. Key kinetochore microtubule-binding components.

Ndc80 complex – highly conserved kinetochore complex required to couple chromosomes to microtubules [68]. It contains four proteins, Ndc80 (Hec1 in humans), Nuf2, Spc24, and Spc25. They assemble together to form two globular domains connected by a long coiled coil that contains a flexible hinge. The globular domain formed by the N-terminal regions of Ndc80 and Nuf2 binds microtubules. Whether Ndc80 alone or Ndc80 and Nuf2 contact the microtubule directly is not yet resolved [48, 69]. Recombinant Ndc80 complexes from yeast, humans, and worms (Caenorhabditis elegans) can couple cargo to assembling and disassembling microtubule tips [36, 46].

Dam1 complex – a 10-protein complex essential for coupling kinetochores to the ends of microtubules in budding yeast [60, 70]. While conserved in fungi, no clear homolog has been identified in higher eukaryotes. In vitro, purified recombinant Dam1 complexes assemble into rings around microtubules [3, 6] and can remain attached to assembling and disassembling microtubule tips while withstanding several picoNewtons of external force [31]. The Dam1 complex also enhances the ability of the Ndc80 complex to attach to dynamic microtubule tips [39, 47] and bear external load [39]. Both the binding of Dam1 complex to microtubules and its interaction with the Ndc80 complex are regulated by phosphorylation [32, 39, 47, 71, 72].

Ska1 complex – containing Ska1, Ska2, and Ska3 (also known as Rama1), the Ska1 complex localizes to kinetochores and along the mitotic spindle [73–78]. In vitro, Ska1 binds microtubules [78]. While present in humans, the Ska1 complex is absent in fungi. The function of the Ska1 complex is still currently under debate. Several groups have proposed that it is a functional homolog of the Dam1 complex [74, 75, 78]. Depletion of Ska1 complex components has been reported to disrupt kinetochore-microtubule attachments [74–76, 78]. In contrast, others find depletion has no effect on kinetochore-microtubule attachments, and suggest the Ska1 complex is involved in silencing the spindle assembly checkpoint [73, 77].

Spc105 complex – essential kinetochore complex localized to the kinetochore throughout the cell cycle in yeast [79, 80]. It is composed of Spc105 (KNL1 in humans) and Ydr532 (also known as Kre28). In vitro, the Spc105 protein of both budding yeast and worms bind microtubules [80, 81], but its contribution to tracking with dynamic microtubule tips has not been tested. KNL-1, the Mis12 complex (also called the Mtw1 or MIND complex in yeast), and the Ndc80 complex together comprise a core microtubule binding unit conserved among eukaryotic kinetochores (and collectively termed the KMN network) [81–83].

Additional evidence supporting the conformational wave mechanism comes from high-resolution electron tomography of microtubule tips in cells. Curled protofilaments emanate from the tips of many kinetochore-associated microtubules [36, 41]. These curls are less sharply bent than those emanating from disassembling tips in vitro, as if the curls in vivo bear tensile load [36]. Consistent with this view, fibrils can sometimes be discerned connecting the curled protofilaments at kinetochore-associated tips to “places deeper in the kinetochore” [36]. However, the significance of these fibrils is controversial [42]. The reduced protofilament curvature seen in vivo could instead be due to any number of microtubule-associated proteins that bind and stabilize this conformation. This interpretation would explain why the curls emanating from tips not associated with kinetochores are also less sharply bent, even though attached fibrils are seen only at kinetochore-associated tips.

The case for biased diffusion

At the molecular scale, thermal forces are paramount. Their importance is easily forgotten, since the smallest structures visible to our naked eye are ten thousand times too large to experience the violent buffeting experienced by protein molecules. Thermal fluctuations are critical for force generation in many cytoskeletal systems. Thus they are very likely to participate in the generation of pulling forces at kinetochores.

The essence of Hill’s thermally-driven biased diffusion mechanism is a multivalent and kinetic attachment to the microtubule lattice. The properties of kinetochore components are strikingly consistent with this picture. Multivalency is a feature of kinetochores in vivo, where microtubule-binding complexes can outnumber the attached microtubules by 8 to 1 or more, depending on the complex and the species [43–45]. At the level of single complexes and small oligomers, both Dam1 and Ndc80 complexes (see Box 3) bind and unbind quickly from the microtubule and, while bound, diffuse rapidly over the lattice [30, 32, 46]. When bound far from the microtubule tip in the absence of external load, their diffusive movement is random (the probability of movement in either direction is equal), However, when Ndc80 complexes encounter a disassembling tip, a bias in their diffusion can be directly observed [46].

Additional support for biased diffusion comes from in vitro motility assays with assembling microtubules. The Dam1 complex [31, 38], the Ndc80 complex [46], and the two complexes together [39] can all maintain persistent, tension-bearing attachments to assembling microtubule tips. This is also true of native kinetochore particles purified from budding yeast (Akiyoshi et al, unpublished results [40]). Given that curled protofilaments are much less prominent at assembling tips [13], and considering that the conformational wave mechanism is based on curled protofilaments, a purely conformational wave-based coupler would be expected to detach more quickly during assembly than during disassembly. In fact, just the opposite is true. These couplers detach far less quickly from assembling tips [31, 38–40, 46]. Moreover, the Dam1 complex sometimes tracks autonomously with growing tips (i.e., it can move with a growing tip in the absence of any external force pulling it toward the tip) [31, 47]. Such assembly-driven pushing cannot be explained by curling protofilaments, since their curling motion is directed back toward the filament lattice. However, it is easily explained by biased diffusion with a preferential affinity for the tip, a known property of the Dam1 complex [6].

Kinetochore components also possess structural features that seem ideal for biased diffusion (Box 2). The Ndc80 complex has a rod- or rope-like structure [5, 48], with one globular end that binds microtubules, another end that anchors to the kinetochore [5, 49], and a flexible hinged coiled coil in-between [50]. A positively charged, disordered ‘tail’ (emanating from the N-terminus of the Ndc80 protein) is crucial for binding the complex to microtubules in vitro [49] and for kinetochore-microtubule coupling in vivo [51, 52]. Likewise, the Dam1 complex binds microtubules through flexible extensions [35]. The disordered, negatively charged E-hook of tubulin may also participate in binding Ndc80 [48, 52] and Dam1 complexes [6] (but see also [35]). The flexibility of these interactions, together with their multiplicity, could enable some to bear load while others unbind and rebind in new locations, allowing a kinetochore to move or reorient on the microtubule without detaching.

A biased diffusion mechanism was also proposed based on the ultrastructure of kinetochores in cells [42, 53]. Their most prominent feature is a web-like mat (the ‘outer plate’) that forms multiple fibrous contacts with the tips of kinetochore-attached microtubules [42, 53]. Some of these fibers orient nearly parallel with the microtubule, extending outward from the mat and making contact with the lattice ~50 nm away from the tip, relatively distant from the curled protofilaments [42, 53]. The molecular identity of these fibers is unknown, but the Ndc80 complex (Hec1 in humans) is a plausible candidate [54]. If they form transient and diffusive attachments to the microtubule lattice, like Ndc80 complex does in vitro [39, 46], they could provide a biased diffusion-based linkage. However, other fibers contact the microtubule tips radially, remaining oriented within the plane of the mat. In principle, curling protofilaments could hook these fibers and tug on them. Thus, as with the rings of Dam1, the fibrous mat structure of the kinetochore is compatible with either the conformational wave or biased diffusion mechanisms.

Forces in vivo and in vitro

To fully evaluate how closely the models, the experiments in vitro, and simulations in silico recapitulate the physiological situation, one must consider how much force is sustained by kinetochore-microtubule junctions in cells. Nicklas’ classic micromanipulation experiments performed over 40 years ago still provide some of the best data (reviewed in [55]). Using a calibrated glass microneedle to pull on chromosomes in meiotic insect cells, Nicklas measured the level of force required to stretch sister kinetochores apart from one another by a given distance. Then, by comparing these measurements with the amount of stretch seen during normal (unperturbed) meiosis, he determined the forces sustained by kinetochore-microtubule junctions. The forces are normally at their highest, 7 pN per kinetochore-attached microtubule, while the sister pairs are bioriented during prometaphase and metaphase. Forces during anaphase are lower, since movement of chromatids after they disengage from one another is resisted only by viscous drag, which is probably < 0.1 pN. Forces as high as 50 pN per microtubule could also be generated when the microneedle was used to apply load opposing the poleward movement of chromosomes during anaphase [55].

Nicklas’ measurements were ground breaking, but their generality remains uncertain. Many cell types are not amenable to direct measurements with microneedles (either because the cells are too small or because they do not survive manipulation). To measure forces in these cells, new approaches are needed. One new method developed for budding yeast is based on the retraction of stretched chromatin after spontaneous breakage of a dicentric chromosome [56]. Data from three retraction events, together with a theoretical model of polymer relaxation dynamics, suggested forces of 0.2 pN prior to breakage [56]. A slightly higher range of forces, 0.5 – 8 pN, was suggested [46] based on published measurements of the extension of pericentromeric chromatin [57], and assuming that force-extension curves for chromatin in vivo are similar to those measured in vitro [58]. Assessing the accuracy and generality of these various estimates will require many more in vivo force measurements. Nevertheless, the data suggest that kinetochore-microtubule junctions normally support 10 pN or less.

Similar forces are sustained in in vitro motility assays with purified kinetochore components. Beads decorated with Ndc80 or Dam1 complexes support 2 to 3 pN while remaining attached to assembling and disassembling microtubule tips [31, 38, 46]. Higher forces, up to ~5 pN, are sustained when Ndc80-decorated beads are used in the presence of free Dam1 complex [39]. This arrangement mimics the physiological situation, where Dam1 assembly onto the kinetochore requires kinetochore-bound Ndc80 complex [59, 60]. Still higher forces, up to 11 pN, are sustained by individual native kinetochore particles purified from budding yeast (Akiyoshi et al, unpublished data [40]). Thus the in vitro assays provide a close match to the normal physiological situation, particularly as more complete kinetochore assemblies are tested. Can either of the two models provide a similar match?

The case is not closed

The literature contains suggestions that the conformational wave mechanism will produce more force than biased diffusion (e.g., [14, 15]), and the latter is sometimes discounted on this basis. However, considering the uncertainty regarding forces in vivo, it is premature to reject either model on the basis of their force-generating capacity.

Using Monte Carlo simulations (as in [46]), it is easy to show that biased diffusion can generate 10 pN or more of pulling force. The absolute maximum force depends on the slope of the steepest portion of the energy landscape, which depends, in turn, on the binding energy of the individual elements and the effective step size for the array (see Box 2). Flexibility between the binding elements, which was not considered in Hill’s original treatment, can decrease the effective step size, thereby increasing the maximum force. Below the maximum force the attachment lifetime will vary with the number of elements in the array, and with their diffusion rate (when tip-bound) relative to the rate of subunit loss from the microtubule. Rapid diffusion of the binding elements on the microtubule surface [30, 32, 39, 46], an experimentally observed behavior ignored in most theoretical treatments, should increase the attachment lifetimes. In our view, more thorough theoretical efforts are needed to explore the limits of the biased diffusion mechanism, particularly now that quantitative data from in vitro measurements can constrain many of the key parameters. The most valuable studies would examine how measurable quantities – such as attachment lifetimes and speeds versus load force, or distributions of rupture force at fixed loading rates – vary as model parameters are adjusted over their full plausible ranges. (As an example, see [61].)

The maximum force that the conformational wave mechanism can generate will depend on the flexural rigidity of a curled protofilament and on the number of curls that pull simultaneously against the load (see Box 1). Theoretical treatments often assume that all the protofilaments pull simultaneously [14, 15, 37, 62], but observations of microtubule tips in vivo suggest that only half of them (i.e., 6 of the 13 protofilaments at each tip, on average [36]) may develop curls long enough to provide a useful power stroke. Protofilament flexural rigidity has not been directly measured, but estimates span a 9-fold range [14, 63–66]. Depending on where their actual rigidity falls within this range, they may or may not be able to generate a working stroke against loads greater than ~2 pN. Thus, the force-generating capacity of both the conformational wave and biased diffusion mechanisms remains uncertain.

Outlook

Based on the strength of in vitro evidence, we believe that biased diffusion is likely to make a substantial contribution to force generation at the kinetochore-microtubule interface. However, determining where the kinetochore falls in the spectrum between pure biased diffusion and pure conformational wave will require experimental tests that exploit the major differences between the mechanisms. For example, the conformational wave hypothesis predicts that coupling will be very sensitive to the structure of the microtubule tip. If the flared protofilaments all break away, leaving a blunt end, the coupler should detach quickly. The degree of flaring at disassembling microtubule tips varies with buffer conditions, which might provide a way to test this idea. The biased diffusion mechanism has fewer structural constraints. Instead, it hinges primarily on the kinetics and energetics of the binding of kinetochore proteins to the microtubule surface. If the bonds are too static, the connections too few, or their affinity too low, the coupler will detach quickly from a disassembling tip. These predictions may be testable using mutations that alter the binding kinetics or diffusion rate in known ways. Ultimately, we predict that kinetochore-microtubule coupling involves contributions from both conformational wave and biased diffusion. The question will then become how these are balanced and regulated throughout the stages of mitosis to achieve precise distribution of the genetic material.

Figure II. Energy landscape and axial force production for a curling protofilament.

(a) Schematic depicting a curling protofilament (red). A segment 5 dimers in length curls out from the microtubule lattice (not shown) and drives movement of an attached kinetochore component (green). Initially, the movement (i → ii) is mainly directed radially outward from the lattice (upward in this view). Later, when a larger angle develops between the protofilament and the microtubule axis, a greater proportion of the movement (ii → iii) is directed productively towards the minus end of the microtubule (rightward in this view). (b) Bending energy stored in the protofilament versus axial position of the bound kinetochore component (i.e., its position projected onto the microtubule axis). Red dots mark energies corresponding to the conformations depicted in (a). As the protofilament relaxes from completely straight (i) into its naturally curved conformation (iii), it loses a total energy represented by g + G, and the bound kinetochore component moves axially by a distance d + D. An intermediate conformation (ii) is also shown to illustrate that a large portion, G, of the total energy is lost during the initial phase of curling, which produces comparatively less axial movement, d. (c) Relationship between axial load and axial deflection for the curled protofilament (which is essentially a semi-circular slender beam [67]). The parameter F represents the amount of opposing load that would suppress the curling by a distance D, enough to eliminate the most productive, second phase of the power stroke. Its value will depend on the effective spring constant for the curl, k = F/D, which in turn depends on the flexural rigidity, EI (see Box 1 text).

Figure III. Energy landscapes for biased diffusion.

Free energy versus position (plotted as heavy black curves) for kinetochores with arrays of M = 3 microtubule-binding elements (green) on a microtubule lattice (red). Parameters w and b represent the net free energy change for detachment of a single element, and the energy change required for a single element to adopt the transition state between sites, respectively. (For simplicity, we also assume here that the transition energy for attachment of a single element to the microtubule is equivalent to b.) Red dots mark energies corresponding to the tip-bound and lattice-bound cases depicted in the cartoons. (a) Energy landscape for a rigid array whose spacing matches the spacing of the microtubule lattice. In this case, the heights of the corrugations, b, 2b, 3b, increase as more elements become bound, up to a maximum of M·b for an array that is fully bound to the lattice. The effective step size, l, is constant. (b) Energy landscape for a flexible array. In this case, the effective step sizes, l, ½l, ⅓l, decrease as more elements are bound, down to a minimum of l/M, and the corrugation heights, b, remain constant.

Experiments show that the corrugation height, b, can be far smaller than the transition energy for detachment (assumed to be w+b for the landscapes shown here). Individual Ndc80 complexes, for example, exhibit lattice diffusion at a rate D_o = 0.17 μm² s⁻¹ [46], implying a very fast rate of hopping from site to site, k_hop = 2,600 s⁻¹ (= D_o/l², where l is taken as 8 nm, the longitudinal spacing of tubulin dimers in the microtubule lattice). Detachment of individual Ndc80 complexes occurs much more slowly, at k_off = 1.2 s⁻¹, implying that the transition energy for detachment must be at least 7.7 k_BT larger than b. This follows from Boltzmann’s law, which relates the energy difference, ΔU, to the ratio of rates, k_hop/k_off = exp(ΔU/k_BT), where k_BT is thermal energy (4.1 pN nm at 25° C).

Glossary

‘Attachment lifetime’

the amount of time a coupler remains attached to a dynamic microtubule tip while bearing a constant load force. Distributions of attachment lifetime can be measured in vitro by using a servo-controlled laser trap to apply constant load while recording the time elapsed between the onset of loading and spontaneous detachment

‘Coupling’

when two distinct but interdependent processes are constrained to happen simultaneously. Examples from biology include the tight coupling between ATP hydrolysis and movement of molecular motors, and the coupling between microtubule shortening and chromosome movement during mitosis. We use ‘couplers’ to refer to kinetochores and reconstituted kinetochore assemblies because they link the growth and shortening of microtubule tips to the movement of cargo

‘Load’ or ‘load force’

the force applied to a molecular motor by its cargo. Examples are the force applied to the kinetochore-microtubule interface by a chromosome in vivo, and the force applied in vitro through a bead held in a laser trap. A load force usually opposes the action of the motor, but in some cases a cargo can exert an ‘assisting’ load

‘Loading rate’

the rate at which load force is increased over time. Faster loading rates result in higher rupture forces

‘Rupture force’

the amount of load force a coupler withstands before detaching. Distributions of rupture force can be measured in vitro by using a servo-controlled trap to increase the load gradually until detachment. (Atomic force microscopes and calibrated glass microneedles can also be used.) Because rupture forces vary depending on how quickly load is applied, it is essential to use a consistent loading rate, and to report the rate that is used (see ‘loading rate’)