A global sensitivity test for evaluating statistical hypotheses with non-identifiable models

SUMMARY

We consider the problem of evaluating a statistical hypothesis when some model characteristics are non-identifiable from observed data. Such scenario is common in meta-analysis for assessing publication bias and in longitudinal studies for evaluating a covariate effect when dropouts are likely to be non-ignorable. One possible approach to this problem is to fix a minimal set of sensitivity parameters conditional upon which hypothesized parameters are identifiable. Here, we extend this idea and show how to evaluate the hypothesis of interest using an infimum statistic over the whole support of the sensitivity parameter. We characterize the limiting distribution of the statistic as a process in the sensitivity parameter, which involves a careful theoretical analysis of its behavior under model misspecification. In practice, we suggest a nonparametric bootstrap procedure to implement this infimum test as well as to construct confidence bands for simultaneous pointwise tests across all values of the sensitivity parameter, adjusting for multiple testing. The methodology’s practical utility is illustrated in an analysis of a longitudinal psychiatric study.

1. Introduction

Sensitivity analysis has been widely advocated in missing data scenarios where the missingness process depends on the unobserved outcomes, as defined in Little and Rubin (1987). Under such missingness mechanism, missing data cannot simply be ignored and unbiased inferences may require strong modelling assumptions, which cannot be checked using the observed data. We consider parametric models, where there are certain parameters of interest in the model for the data and other parameters in the missingness model which may be viewed as secondary parameters. In addition to the form of the parametric model not being identifiable, in many cases, the models may be ”overparameterized”, so that even if the form of the model is correct, standard estimation techniques may still fail due to the models being non-identifiable. This is problematic, since it may not be known a priori whether identifiability holds, owing to the complex nonlinear structure of the missing data models. In practice, these problems may be manifested in unstable estimation, where the algorithms used to compute the estimators may not converge reliably.

In order to make inference about the parameters of interest without simultaneously estimating all model parameters, one may instead fix a minimal set of parameters, called sensitivity parameters, conditional upon which the primary parameters are assumed identifiable. These profile models, viewed as functionals of the sensitivity parameters, provide the basis of sensitivity analysis. In essence, one uses the model profiled across the sensitivity parameters as a working model to delineate inferences consistent with the observed data. Two general strategies for sensitivity analysis have been discussed in the literature, local and global, depending on the range of the sensitivity parameter under consideration. A local sensitivity approach assesses the impacts of uncertainties on inferences over a range of models specified by the sensitivity parameter in a small “neighborhood” of a known value of this parameter (Copas and Eguchi, 2001; Verbeke et al., 2001; Troxel et al., 2002; and Todem et al., 2006). The idea stems from work on missing data, where one may assess the effects of small perturbations of the ignorable model in the directions of non-ignorable models. The sensitivity of the identifiable parameter with respect to sensitivity parameters may be estimated via partial derivatives with respect to the sensitivity parameter in a neighborhood of the sensitivity parameter values corresponding to ignorable missingness. If the parameter estimates are locally insensitive to these values of sensitivity parameters, then, under the assumption of small violations of ignorability, the hypothesis can be reasonably evaluated assuming ignorable missingness. Such methodology is useful but does not permit assessments of large deviations of sensitivity parameters on inferences. In practice, it may be of scientific interest to understand the impact of such deviations. Global analyses may be critically important in such applications. Under qualitative assumptions regarding the missingness mechanism, it may be possible to derive such bounds without imposing further parametric assumptions; see Manski (2003) and Horowitz and Manski (2006) for overviews. Such ideas have been explored empirically, as in Scharfstein, Manski and Anthony (2004) for observational studies. Alternatively, one may employ more structured parametric models for the missingness mechanism. Such modelling approaches are commonly employed in practical data analytic settings, owing to their conceptual simplicity and ease of implementation. Similarly to our set-up, there are a small number of sensitivity parameters. Recent illustrations of such methodology can be found in Shepherd et al (2006) and Vansteelandt et al (2006). A limitation is that formal inference is not provided. The usual strategy for presenting results is to provide parameter estimates at various values of the sensitivity parameters, accompanied by pointwise confidence intervals based on the assumption of a correctly specified model. Inference regarding significance of the covariates is ad hoc, ignoring that multiple tests are conducted and that the model may be misspecified.

In Section 2, we propose conservatively testing the null hypothesis across the support of the sensitivity parameter using an infimum test statistic. The test accounts for the facts that inferences are carried out simultaneously across the entire range of the sensitivity parameter and that the model is misspecified under certain values of the sensitivity parameter, as there is only a single true value. We also develop simultaneous confidence bands for the identifiable parameter, enabling pointwise tests which control the overall type I error rate and an assessment of the magnitudes of the effects, over the range of the sensitivity parameter. These procedures require a careful theoretical analysis of the estimator as a process in the sensitivity parameter; asymptotic properties are sketched in the text, with details in a supplementary web file. A bootstrap procedure is suggested for practical implementation. In Section 3, we present a special case of our general working model set-up, a shared random effects model for longitudinal binary outcomes with non-random dropouts. We discuss identifiability issues related to the proposed model and describe aspects of estimation and inference. A practical illustration of the sensitivity analysis for this model using a psychiatric data set is given. We conduct a simulation study assessing the performance of the sensitivity tests in small samples. A discussion concludes in section 4. Additional technical details are contained in a Supplementary Materials file.

2. The general framework

2.1 Overview

Consider a random process of any finite dimension W ~ f_W(θ;W), where f_W(θ;.) is a parametric family known up to a parameter vector θ ∈ Θ. As an example, in the context of meta-analysis on publication bias one may take W = (Y, R), where Y is observed for R = 0 and missing for R = 1. In the context of longitudinal studies with T potential outcomes for each subject, one would take Y = (Y₁, …, Y_T)′, and R = (R₁, …, R_T)′, where R_t = 1 if Y_t is unobserved and 0 if otherwise. Suppose that n independent copies W₁, W₂,…, W_n of W are available and that consistent estimation of θ may not be possible as a result of identifiability issues. That is, the maximum likelihood estimate of θ namely,

$$\widehat{\theta }={\text{argmax}}_{\theta \in \mathrm{\Theta }}{\displaystyle \sum _{i=1}^n\text{ln}{f}_w(\theta ,W_i),}$$

may not have good properties. The nonidentifiability of the model can be managed by considering a parameter say δ, conditional upon which the others are estimable. The model parameter vector can then be partitioned as θ = (ψ, δ), where ψ is assumed identifiable for a fixed δ. The usual strategy for presenting results is to provide the maximum likelihood parameter estimates ψ̂(δ) of ψ at various values of δ, accompanied by pointwise confidence intervals based on the assumption of a correctly specified model. Inference regarding significance of identifiable model parameters is ad hoc, ignoring that multiple tests are conducted and that the model may be misspecified. Previous work on complex parametric models has overlooked these two key issues, the first being that inference must be made simultaneously across a continuum of the sensitivity parameter and the second being that the missingness model will be misspecified at virtually all values of the sensitivity parameter within that continuum. The theoretical analysis below provides the necessary results for dealing with these issues. In particular, the development of the sensitivity tests in the next subsection depends critically on a careful study of the properties of the ψ̂ (δ).

2.2 Uniform asymptotic properties of profile likelihood-based estimators

To ensure that the profile likelihood function is bounded for any value of δ, we restrict ℋ, the support of δ, to a compact set. It is well known that under a correctly specified model fit with δ = δ₀, the true value of δ, and under mild regularity conditions, the estimators are consistent and asymptotically normal, that is,

$$n^{\frac{1}{2}}\left\{\widehat{\psi }({\delta }_0)-{\psi }_0\right\}{\to }_{d}N(0,\mathrm{\Sigma })\text{and}\widehat{\psi }({\delta }_0){\to }_p{\psi }_0$$

as the sample size n gets large, where ψ₀ is the true value of ψ with δ fixed at δ₀. Under a misspecified dropout process, i.e. δ ≠ δ₀, and for a large n, we get ψ̂ (δ) →_p ψ_*, with ψ_* not necessarily equal to ψ₀. The vector ψ_* will typically depend on δ and will be denoted ψ_*(δ) to highlight this dependence. When n → ∞, the pseudoscore functions are roughly quadratic in the neighborhood of ψ_*(δ) for fixed δ and the limiting distribution of $n^{\frac{1}{2}}\{\widehat{\psi }(\delta )-{\psi }_{*}(\delta )\}$ is mean zero normal with variance-covariance matrix Γ (δ) (White, 1982).

These pointwise results may be made uniform under certain smoothness conditions, using empirical process arguments. Under conditions C1 and C2 in the Supplementary Materials, ψ̂ (δ) is uniformly consistent for ψ_*(δ) and J(δ) = n^1/2{ψ̂(δ) −ψ_*(δ)} converges weakly to a Gaussian process with mean 0 and covariance function E{J(δ₁)J(δ₂)′} = Γ(δ₁, δ₂) = E{ι_i(δ₁)ι_i(δ₂)′}, where the influence function ι_i(δ) is defined in (A3) in the Supplementary Materials. In general, estimates at different values of the sensitivity parameter will be highly correlated and treating the estimates as independent could lead to misleading inferences. An estimate of Γ(δ) based on the inverse of the observed information matrix from the profile likelihood is known to be biased, due to the model misspecification. McCullagh and Tibshirani (1990) have shown that some adjustments can be made in order to reduce the bias to O(1/n). An alternative is to use a robust sandwich variance estimator as described by White (1982), which can be computed as $\widehat{\mathrm{\Gamma }}({\delta }_1,{\delta }_2)=n^{-1}{\displaystyle {\sum }_i\widehat{{\iota }_i}({\delta }_1)}\widehat{{\iota }_i}\prime ({\delta }_2)$ where ι̂_i is ι_i with all unknown quantities replaced by empirical estimators. One may also use the bootstrap method to estimate the standard errors of the estimates of the parameter ψ_*(δ) (Efron and Tibshirani, 1993). The method consists of randomly selecting S samples of size n with replacement from the original data set, where the sampling units consist of all information collected on each individual, W_i, i = 1,…, n. The sample standard deviation of the parameter estimates from the n bootstrap samples estimates the true standard error. This bootstrap procedure may also be used to approximate the distribution of ψ̂(δ) as a process, which is quite complex and does not lead to simple analytic testing procedures. The validity of the bootstrap follows automatically from empirical process theory under the regularity conditions given in Appendix A (van der Vaart and Wellner, 2000), essentially requiring the smoothness and boundedness of the likelihood for fixed δ ∈ ℋ. This occurs because even though the model may be misspecified, the estimand ψ_*(δ) is an implicit functional of the empirical distribution so that empirical process theory applies equally under correctly specified and misspecified models.

Condition C2 in the Supplementary Materials underlying all of the above results requires that a unique ψ_*(δ) exists after fixing δ. In fact, to our knowledge, a rigorous analysis of ψ̂(δ) accounting for model misspecification has not previously been undertaken. Formally establishing this condition is beyond the scope of this paper.

2.3 Global sensitivity testing

Suppose we are interested in evaluating the following null hypothesis:

$${\mathrm{H}}_{01}:C\psi =c,$$

where C is an r × p contrast matrix and c is an r × 1 vector of constants. This framework allows for composite hypotheses. In the special case of testing whether the jth coefficient of ψ is equal to 0, one takes C to be 1 × p vector with a one in the jth position and zeros elsewhere and c = 0. Under a nonidentifiable model, the above hypothesis cannot be tested without additional restrictions. If the true sensitivity parameter δ₀ is known, the true hypothesis to be evaluated is given by H₀₂ : Cψ_*(δ₀) = c, where ψ_*(δ₀) = ψ₀. Unfortunately in most cases, δ₀ is unknown and may not be estimable from observed data. We propose a global sensitivity test which uses the trivial inequalities given by,

$$\underset{\delta }{\text{inf}}\Vert C{\psi }_{*}(\delta )-c\Vert \le \Vert C{\psi }_{*}({\delta }_0)-c\Vert \le \underset{\delta }{\text{sup}}\Vert C{\psi }_{*}(\delta )-c\Vert ,$$

to make rigorous inferential statements about H₀₂. Here ‖·‖ is any norm function, typically Euclidean norm. We can evaluate H₀₂ by conservatively testing the hypothesis inf_δ ‖Cψ_*(δ)−c‖ = 0. Clearly when inf_δ ‖Cψ_*(δ) − c‖ is strictly greater than zero, ‖Cψ_*(δ₀) − c‖ will be greater than zero as well. The infimum hypothesis is formally defined as

$${\mathrm{H}}_{03}:\underset{\delta }{\text{inf}}\Vert C{\psi }_{*}(\delta )-c\Vert =0.$$ (1)

In the case of a one-dimensional parameter ψ, an ad hoc test may be conducted by constructing simultaneous confidence bands for ψ_*(δ) given δ. If the band includes 0 for any δ, then H₀₂ cannot be rejected. In general, if a simultaneous confidence band for Cψ_*(δ) excludes c for all δ, then one rejects the associated null. Note that such bands also identify those δ at which the null is rejected, which may be useful in understanding how inferences change as a function of the missingness model.

We now propose a formal infimum statistic to evaluate H₀₃,

$$T=\underset{\delta }{\text{inf}}\left\{(C\widehat{\psi }(\delta )-c)\prime {(C\widehat{\mathrm{\Sigma }}(\delta )C\prime )}^{-1}(C\widehat{\psi }(\delta )-c)\right\}$$

where Σ̂(δ) is an estimator of the variance-covariance matrix of ψ̂ (δ). The test statistic T rejects the null for unusual large values. While for each fixed δ, the test process follows a simple chi square distribution under the null, the asymptotic distribution of the estimator ψ̂ (δ) as a process in δ is quite complicated and the distribution of T is analytically intractable. One may use the nonparametric bootstrap to generate the distribution of the infimum test statistic and to construct the confidence bands, using the approach described in section 2.2. Let ψ̂^s(δ) and T^s, s = 1,…, S denote the estimators and infimum tests computed in the S bootstrap samples. One rejects the null at level α if the observed test statistic is larger than the (1 − α) percentile of empirical distribution of T^s, s = 1,… S. A simultaneous confidence region for Cψ_*(δ) − c takes the form

$$\{x(\delta ):\mathscr{H}\to R^r;\Vert x(\delta )-C\widehat{\psi }(\delta )+c\Vert <{\widehat{\vartheta }}_{\alpha }\},$$

where ϑ̃_α as the (1 − α)th empirical percentile of ${\{{\text{sup}}_{\delta \in \mathscr{H}}\Vert C{\tilde{\psi }}^s(\delta )-C\tilde{\psi }(\delta )\Vert \}}_{s=1}^S$.

A pointwise approach might also be used to perform a sensitivity analysis for ‖Cψ_*(δ)−c‖ = 0 given a finite number of values for δ. The method consists of letting the sensitivity parameter take values in a set A = {δ₁, …,δ_Q} ⊂ R⁺, with Q < ∞ and evaluating the hypothesis, ‖Cψ_*(δ) − c‖ = 0. Specifically, for δ ∈ A, simultaneous pointwise confidence intervals may be constructed for {Cψ_*(δ) − c} using standard error estimates for ψ̂ (δ) from section 2.2, with a multiplicity adjustment. If all intervals exclude 0, then Cψ_*(δ) ≠ c at those δ. This approach should be carefully undertaken as the choice of points in A may be somewhat arbitrary and may miss δ where H₀₃ holds. Thus, one cannot formally test H₀₁ using finite δ. Moreover, there may be reduced power with large Q, where the multiplicity adjustment for controlling the overall type I error may be quite conservative. The global approach described above provides a systematic method for dealing with these issues.

3. Application to longitudinal outcomes with potentially non-random dropouts

3.1 A shared random effects model as a working model

We consider a longitudinal study where for each subject i = 1,…,n, there are T potential outcomes Y_i1,…, Y_iT represented by the vector Y_i(𝒞) = (Y_i1,…, Y_iT)′, measured at discrete time points in 𝒞 = {t₁,…, t_T}. These outcomes, however, may not be fully observed and therefore are coupled with a missingness indicator R_i = (R_i1,…, R_iT)′, where R_it = 1 if Y_it is unobserved and 0 if otherwise. When the missing data result from dropouts, it is intuitive to represent the series of missingness indicators by a single random variable denoted by D_i = 1 + max{t : R_it = 0}, which indicates the drop-out time for subject i. We assume that D_i ≥ 2 which implies that all subjects are present at first time point. If D_i = T + 1 then the subject is fully observed and if D_i < T + 1 the subject drops out.

Although our analysis can be performed for a wide variety of models, to minimize incidental technicalities, we consider the special case of random intercept models with potentially not at random missing values. We consider a conditional mean model, μ_it = pr(Y_it = 1 | b_i, X_it), for an hypothetical response Y_it given some random effects b_i as,

$${\mu }_{\mathit{\text{it}}}=g^{-1}(X_{\mathit{\text{it}}}\beta +b_i).$$

Here g is a monotone, differentiable and invertible function, and β = (β₁,…, β_p) is the slope vector associated with fixed covariate X_it. The random variable b_i is assumed to be generated from a central normal distribution with variance τ². This mean model is suitable for analyzing data for which the primary interest is the assessment of subject’s level contrasts. It is well known that this family of models produces fixed effects parameters that have a subject-specific interpretation.

We allow the discrete dropout hazard, h_itj = pr(t_Di = t_j | t_Di ≥ t_j, b_i, Z_itj) at discrete time point t_j ∈ 𝒞, to depend on the hypothetical complete measurement series Y_i(𝒞) through the unobserved covariate b_i. Specifically, we assume the model,

$$\mathit{\text{log}}\{h_{\mathit{\text{it}}}/(1-h_{\mathit{\text{it}}})\}=\epsilon (Z_{\mathit{\text{it}}})\alpha +\delta \varphi (b_i),$$

where ε(Z_it) is an appropriate function of fixed covariates Z_it with associated coefficient α. The parameter δ, assumed positive, is the slope associated to the transformed random effects ϕ(b_i). The function ϕ (.) is a nondecreasing function such that 0 < ϕ(b_i) < 1, for all b_i, and attains the boundaries at the limits, that is lim_bi→−∞ ϕ(b_i) = 0 and lim_bi→∞ ϕ(b_i) = 1. Note that the function ϕ(.) can suitably be modified when b_i has a finite support. We can reparameterise the function ϕ (.) by writing ϕ(b_i) = (1 + e^−η(b_i))⁻¹ for all b_i on the real line. The function ϕ(.) imposes the following restrictions on η(.), lim_bi→−∞ η(b_i) = −∞ and lim_bi→∞ η(b_i) = 1. Any such function ϕ(.) that meets the conditions above defines a function η(.) and vice versa.

The idea of using a shared random effects model for modeling longitudinal outcome subject to dropouts not at random is not new (see for example, Wu and Carroll, 1988; Albert and Follmann, 2000 and Ten Have et al., 2002). This class of models is very attractive in the context of unbalanced longitudinal studies. Our extension of the shared random effects technique is the introduction of the function ϕ(.) and restriction of the parameter δ to be positive. The function ϕ(.) is assumed to be bounded, monotone, differentiable and invertible. These constraints endow the parameter δ with a meaningful interpretation as an odds ratio for treatment assignment inequality (Rosenbaum, 2002), where the unobserved variable is constrained to the interval [0, 1]. Our constraint satisfies this condition, with the boundaries 0 and 1 attained at the limits. Here, the odds ratio of drop-out hazard between two subjects i and i′ with same fixed covariate vectors, Z_it = Z_i′t is bounded as

$$\text{exp}(-\delta )\le \frac{h_{\mathit{\text{it}}}(1-h_{i\prime t})}{h_{i\prime t}(1-h_{\mathit{\text{it}}})}\le \text{exp}(\delta ),\text{with}\delta >0.$$

In other words, for δ > 0, exp(δ) is a measure of the degree of departure from a study with a random dropout mechanism.

For the random effects model above, joint identifiability of the data and missingness models has not been established. A natural choice of sensitivity parameter is δ, which measures the extent of non-randomness of the dropout process. It is clear that when δ = 0, the two processes can be separately identified and the dropouts and completers have the same distributional properties. Treating the fixed, possibly non-zero, value of δ as the true value, one may form a working likelihood under the random intercept model, assuming conditional independence of the outcomes and the missingness given random effects. The inference procedure we discuss below is valid assuming that ψ_*(δ) is identifiable conditionally on δ, regardless of the joint identifiability of the outcome model and the missingness model. Interestingly, even for the case of fixed δ, formal conditions for identifying ψ_*(δ) have yet to be developed.

Under mild conditions, for large δ the profile log-likelihood diverges and the maximum likelihood solution does not exist (proof shown in Supplementary Materials). That is,

$${\displaystyle \sum _{i=1}^{n_d}\text{log}{l}_d^i(\psi |\delta )+{\displaystyle \sum _{i=n_d+1}^n\text{log}{l}_o^i(\psi |\delta )\to -\infty ,\text{as}\delta \to \infty ,}}$$

where n_d = ∑_i I(D_i ≤ T) is the number of subjects dropping out prior to end of study, after a rearrangement of the data set. This supports the above constraint that δ is bounded. Hence, we assume without any loss of generality that δ lies in a compact set, that is δ ≤ Δ with 0 < Δ < ∞. In practice, the upper bound should be chosen so that the algorithm converges for all δ ≤ Δ.

3.2 Analysis of psychiatric data

A good example of a longitudinal study with potentially non-random dropouts is the Fluvoxamine (a serotonin reuptake inhibitor) clinical trial. This is a multi-center non-comparative study, designed to reflect clinical practice closely with out-patients diagnosed with depression, obsessive-compulsive disorder or panic disorder. Accumulated experience in controlled trials has shown that Fluvoxamine is as effective as conventional tricyclic antidepressant drugs, and more effective than placebo in the treatment of depression (for a review, see Burton, 1991). However, many patients suffering from depression have concomitant morbidity associated with this condition, potentially leading to dropout. It was then decided to set up a post-marketing pharmaco-vigilance trial to study more accurately the profile of Fluvoxamine in ambulatory clinical psychiatric practice. A total of 315 patients with a diagnosis of either depression or obsessive-compulsive or panic disorder were enrolled in the study. All subjects were treated with Fluvoxamine in doses ranging from 100 to 300 mg/day and underwent clinical evaluations at baseline, 2, 4, 8 and 12 weeks. One primary endpoint comprised the side effects of the drug recorded on an ordinal scale. Several patient’s baseline characteristics such as sex, age, initial severity of the disease on a 1 to 7 scale, and duration of the mental illness were recorded. A full description of the study is given by Molenberghs and Lesaffre (1994), Lesaffre et al. (1996) and Kenward et al. (1994).

One key objective of the study was to assess the within-subject evolution of side effects over time, accounting for dropouts. For simplicity and ease of interpretation, our analysis of the within-subject evolution (captured by time effects) is based on a dichotomized version (presence/abscence) of side effects, as opposed to ordinal outcomes, regardless of the baseline characteristics. A side effect occurs if new symptoms appear.

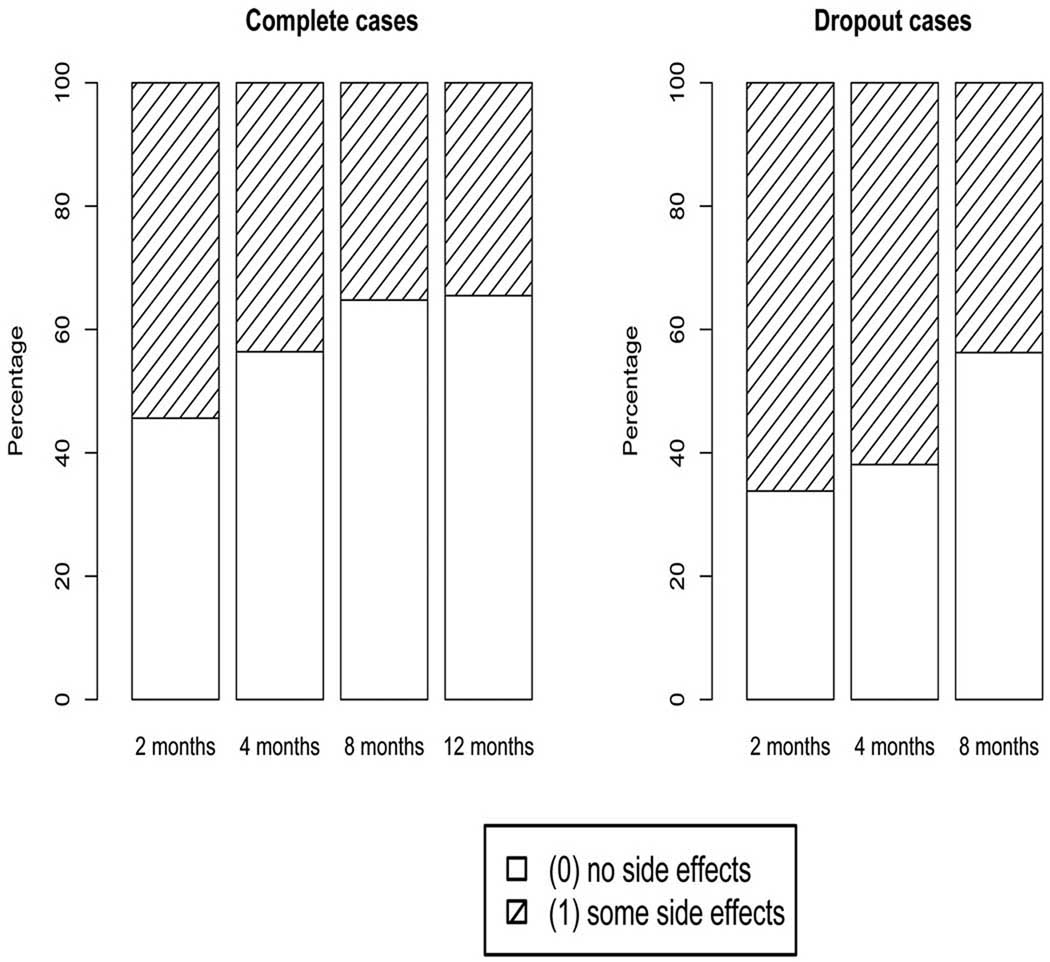
Figure 1 shows the empirical distribution of side effects over the four time points for the complete (full-sequence) cases and over the first three time points for dropout cases. Out of 315 patients, 224 patients had a full-sequence data resulting from the fact that 14 subjects were not observed after recruitment, 31, 26, and 18 patients dropped out, respectively, after the first, second and third visit and 2 patients had a non-monotone missing pattern. We ignore the 2 cases that had a non-monotone missing pattern as well as the 14 patients that dropped out before the first visit (at 2 months). Compared to the start of the study, a drastic reduction of side effects is depicted throughout the study for the completers compared to the dropout cases. Specifically, about 54% of patients who complete the study had some side effects at 2 months compared to 66% for subjects who did not complete the study. At 4 months, 44% of completers had some side effects compared to 62% for subjects who did not complete the study. And finally, at 8 months, 35% of completers had some side effects compared to 44% for subjects who did not complete the study. Clearly, the study non-completers are doing more poorly with respect to side effects. A naive analysis that ignores this selection process might lead us to conclude that the side effects drastically diminish over time in the studied population. A question emerges: How do side effects evolve over time within a patient when dropouts are accounted for?

Figure 1.

Evolution of observed side effects for all complete cases over observed time points

As a preliminary analysis, we first fit a random subject effect model to the side effects response with only fixed linear time effects both to completers and non-completers. The measurement model is given by, pr(Y_it = 1|b_i,X_it) = {1 + exp(−β₀ − β₁X_it − b_i)}⁻¹, where {Y_it = 1} indicates the presence of some side effects and X_it represents the value of the time covariate for subject i at time point t. The results of the time slope estimates (standard errors) are −.75 (.13) for the complete cases and −.23 (.28) for the incomplete cases. The results of this analysis are consistent with those of the bar charts shown in Figure 1. In particular, the time effect on side effects appears larger (in magnitude) for the analysis based on the completers. Hence, subjects who dropped out prematurely from the study are likely to suffer more side-effects, although the estimate fails to reach statistical significance.

Following the sensitivity testing strategy described in section 2.3, we first fit the ignorable model to assess the effect of time on the side effects outcome. The result of β̂₁(0), the time slope estimate (standard error) is −.76 (.12) using all available cases. The ignorable model clearly suggests a significant linear time effect (p-value < .0001).

We next attempted to simultaneously estimate δ and ψ via maximum likelihood Unfortunately, the computations were unstable. Multiple starting values were tried. In some cases, the algorithm diverged, while in cases where it did converge, multiple local maxima were obtained. This suggests that the model is at best weakly identified on the psychiatric data.

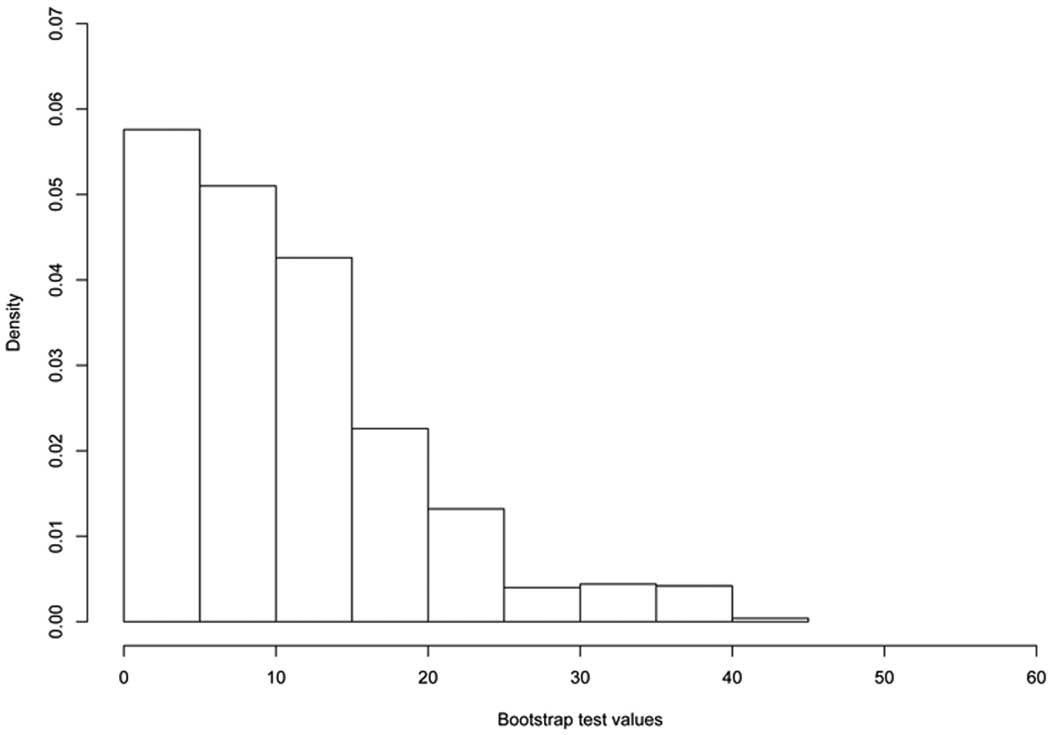
In order to conduct inferences which do not require joint identifiability of the data and missingness models, we evaluate the hypothesis inf_δ |β_*,1(δ)| > 0 using the infimum test under the shared random effects with a dropout model given by; log{h_it/(1 − h_it)} = α₀ + α₁X_it+δϕ(b_i). Our sensitivity analysis was restricted to the range [0, 80] as values of δ above 80 yields unstable estimates. We perform the infimum test based on 1000 bootstrap samples, using the statistic T = inf_δ {β̂₁(δ)′Σ̂(δ)⁻¹ ββ₁(δ)}. The observed value of the infimum test statistic is T^obs = 40.90, which is highly significant at 1% level (p-value < .0001) (see the histogram of bootstrap test samples in Figure 2). This test suggests that inf_δ |β_*,1(δ)| is greater than zero and it can then be concluded that the true time effect measured by |β_*,1(δ₀)| is greater than zero.

Figure 2.

Histogram of the 1000 bootstrap sample test statistics generated under the null hypothesis

One might criticize the choice of the upper bound Δ = 80 as being scientifically unreasonable. We believe that this choice reflects an extreme scenario, which may be of scientific interest, albeit one which is a priori unlikely. The main concern is that contemplating such scenarios leads to a null hypothesis which reflects an overly conservative worst case scenario. Interestingly, in this example, the evidence for the covariate effect is rather strong, so that the infimum test rejects over this wide interval. Moreover, in general, considering such a wide range for δ enables one to construct confidence regions for δ for which |β_*,1| > 0, which is practically useful. That is, one can determine all values of δ for which a non-zero covariate effect exists, accounting for simultaneous inference across many δ.

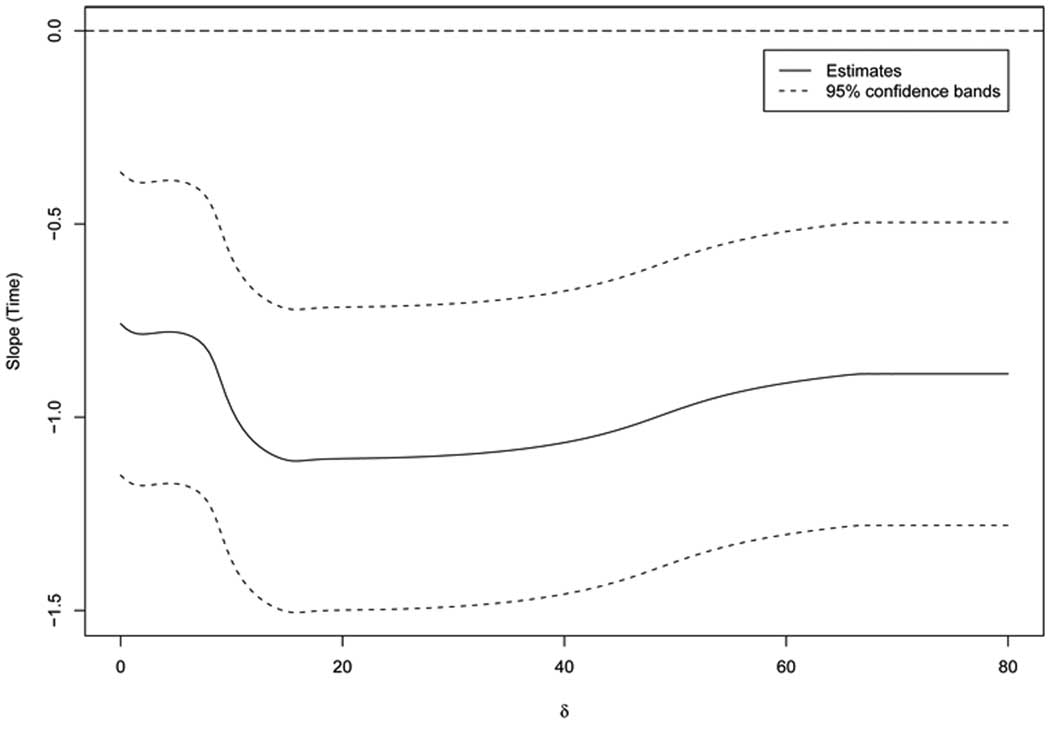
To illustrate how the magnitude of the covariate effect changes as the sensitivity parameter is varied, we also computed simultaneous 95% confidence bands for β_*,1(δ) for δ ≤ 80 (see Figure 3). All simultaneous confidence intervals exclude 0, which is in agreement with the infimum test above. The largest time effect is achieved when δ ≈ 15.

Figure 3.

Estimate of time slope for fixed values of the sensitivity parameter δ and corresponding 95% simultaneous confidence bands using the side effects data from the Fluvoxamine study

This example illustrates that it may be useful to conceptualize a sensitivity analysis in terms of testing the smallest covariate effect over the range of the sensitivity parameter when the true effect is not identifiable from the observed data. The approach is especially useful in high-risk situations where a worst case analysis may be helpful. For the Fluvoxamine data set, the linear time effect exits regardless of the sensitivity parameter. In addition, we found that the estimate of the time effects ranges between −1.15 and −.74 given values of the sensitivity parameter. Hence, the estimated odds for showing some side effects can be multiplied by a factor as small as .32 and as much as .48 for each unit increase in time. The 95% confidence bounds run from roughly −1.50 (smallest value on lower bound across all δ) to −.50 (largest value on upper bound across all δ). This could be viewed as a conservative 95% confidence interval for the unknown β₁ = β_*,1(δ₀).

In this example, the global analysis is essential since the estimate of the parameter being tested does not increase or decrease monotonically as the sensitivity parameter is increased or decreased. An explanation is that the joint measurement-missingness model is highly nonlinear, so that there may be a complex relationship between β_*(δ) and δ, which may not be monotone in δ. Under monotonicity, it is only necessary to evaluate β_*(δ) at the lower and upper bounds of the sensitivity parameter space in order to test the null hypothesis. With non-monotone behavior, such tests may yield misleading results.

3.3 Simulations

We report results of a small simulation study evaluating the performance of the infimum test under the null when the dropout process is related to unobserved responses. The simulations were conducted so as to roughly approximate data from the Fluvoxamine study. In each Monte Carlo iteration, we simulated a sample of n subjects with four potential measurement time points (T = 4), using the outcome model pr(Y_it = 1|b_i, X_it) = {1+exp(−β₀−β₁X_it−b_i)}⁻¹, where b_i ~ N(0,2) and X_it = t takes values in {1, 2, 3, 4}. The dropout observations were generated using the dropout hazard model log{h_it/(1 − h_it)} = α₀ + α₁X_it + δ₀ϕ(b_i). To keep the simulation simple, we set α₁ = 0 to constrain the instantaneous dropout probability to be time independent and β₁ = 0, so that the null is satisfied. We produced 20 – 60% dropout using both an ignorable (β₀ = 0) and a non-ignorable (β₀ = 3) missing data models. This process was repeated for 1000 Monte Carlo replications. The infimum tests were computed using 1000 bootstrap samples for δ ≤ 10.

Table 1 shows the results of this simulation study for sample sizes equal 25, 50, 100, and 250 and nominal test levels equal to .01, .05, and .1. Asymptotic standard errors (as the number of Monte Carlo iterations tends to infinity) are reported in the last row of the table. Overall, the tests perform well, with the bootstrap distribution of the test providing a reasonable approximation to the nominal level even in fairly small samples (n = 25). As expected, for increasing sample sizes, the empirical rejection rates agree more closely with the true significance levels under the null.

Table 1.

Monte carlo empirical rejection rates in simulations study

True dropout model			Sample size
Mechanism	% dropout	(α0, δ0)	n=25			n=50			n=100			n=250
			Nominal test level			Nominal test level			Nominal test level			Nominal test level
			.01	.05	.10	.01	.05	.10	.01	.05	.10	.01	.05	.10
Random	20	(2.55, 0)	.010	.080	.155	.006	.081	.158	.009	.072	.129	.007	.064	.124
dropouts	40	(1.67, 0)	.013	.065	.143	.014	.073	.148	.017	.060	.127	.013	.055	.119
	60	(1.02, 0)	.004	.067	.150	.001	.043	.112	.004	.050	.118	.012	.057	.114
Non-random	20	(1.34, 3)	.014	.071	.152	.014	.073	.150	.011	.063	.138	.014	.063	.118
dropouts	40	(.34, 3)	.012	.098	.178	.006	.054	.133	.006	.067	.131	.010	.074	.122
	60	(−.52, 3)	.007	.059	.130	.008	.037	.099	.012	.064	.127	.015	.058	.125
Monte carlo s.e.			.003	.007	.009	.003	.007	.009	.003	.007	.009	.003	.007	.009

4. Discussion

In this paper, we have shown how a statistical hypothesis can be evaluated using a joint parametric model for the measurement and missing data processes, when some model characteristics are non-identifiable. We proposed an approach in which hypothesized parameters are viewed as a functional of a non-identifiable sensitivity parameter. A conservative testing procedure was employed based on an infimum statistic over the range of the sensitivity parameter. Similar approaches based on confidence bounds have been studied for global sensitivity analyses under qualitative restrictions. Our approach differs in that we work with parametric models and rigorously delineate the full spectrum of inferences consistent with the model assumptions. Previous work with parametric models has not addressed key issues inherent in such formulation, including multiple testing and model misspecification. Our methodology enables the construction of simultaneous confidence bands which pinpoint those values of the sensitivity parameter at which significance is achieved, as well as a comparison of the magnitude of the effects across the sensitivity parameter.

Obtaining the sensitivity parameter region over which a covariate effect is significant may be particularly important in scenarios where the effect does not increase or decrease monotonically as the sensitivity parameters are increased or decreased. In practice, missing data models are often quite complicated and it may not be clear whether monotonicity holds. In these set-ups, a global sensitivity analysis is the most conservative data analytic strategy. For the Fluvoxamine example, the infimum test shows that the linear time effect exists, regardless of the sensitivity parameter, while the confidence bands demonstrate that the magnitude of the effect is non-monotone. These findings are extremely important for the drug company which may be interested in knowing how the side effects evolve within a subject as a function of the drop-out mechanism.

Although the method is presented in the context of likelihood based analyses, with a focus on generalized linear mixed effects models for binary outcomes in time with non-ignorable dropouts, the method can easily be applied to other situations where any component of the model is non-identifiable from observed data and non-likelihood based methods of analysis are available, for example, generalized estimating equations. Further research is needed to show how to choose the sensitivity parameter in other model settings. The choice of the sensitivity parameter from a statistical perspective is non-unique, so long as identifiability is induced in the appropriate sense. However, a careful choice may lead to simplifications in the computations (Kenward et al., 2001). The subject matter is also instrumental in guiding the investigator in the choice of the sensitivity parameter.

Additional work is needed to show how to apply the global test in situations where more than one dimension of the model may be non-identifiable. For example, for our working random effects model, multiple sensitivity parameters could be considered, if it was deemed necessary for identification purposes. The parameters in the shared random effects distribution might be treated as sensitivity parameters along with the parameter δ, yielding a multidimensional problem. The infimum test can then be constructed over a class of distributions for the random effects along with values of δ. The computational burden of such tests will increase with the dimension of the sensitivity parameter and be burdensome in some setups. The computational issues require careful study. Another issue is that we restrict δ to be bounded. It would be useful to permit the sensitivity parameters to be unbounded. While this is conceptually straightforward, it poses certain theoretical challenges which are not easily addressed. This is a topic for future research.