Table 2. Validating network growth models via the confusion matrix.
| DMC(0.1,0.9) | DMC(0.5,0.5) | FF(0.2) | PA(5) | PA(15) | |
| Reverse DMC | 55.6/45.5 | 24.4/38.3 | 49.5/41.7 | –/58.8 | –/64.0 |
| Reverse FF | 1.8/33.1 | 10.7/37.2 | 54.5/54.5 | –/28.4 | –/24.4 |
| Reverse PA | –/35.0 | –/35.0 | –/50.6 | –/72.6 | –/88.9 |
| Node degree | –/39.3 | –/38.1 | –/59.2 | –/75.2 | /–85.5 |
| Centrality | –/39.2 | –/37.9 | –/57.5 | –/74.9 | –/85.3 |
Column headings show the model and parameters used to grow the random graph forward. Row labels show the model used in the reversal (assuming optimal parameters). For the node degree reconstruction (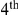
row), we removed nodes in increasing order of their degree in the extant network (nodes with the same degree were ordered randomly). For the centrality reconstruction (
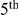row), we removed nodes in decreasing order of their closeness centrality in the extant network. Each cell contains Anchor/Footrule scores (PA, node degree, and centrality do not generate Anchor scores). Performance was averaged over 1000 runs. Bolded cells indicate best performance. For example, for DMC random graphs with 
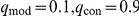, reversing with FF produces a 33.1% Footrule score compared to a 45.5% score when the graph is reversed with DMC itself. The non-model-based heuristics produce good age-estimates when applied to models where degree is known to be correlated with age (FF and PA) as is expected; however, the downside to these approaches is that they do not produce a likelihood estimate for ancestral graphs, nor do they predict node anchors. For identifying anchors and for DMC age estimates, reversing with the model used to grow the graph forward resulted in the best performance.