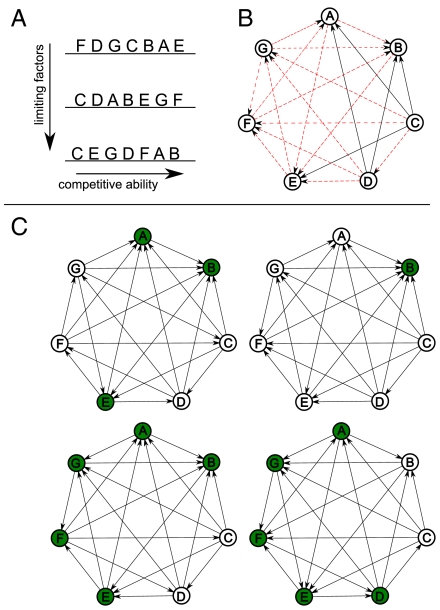
Fig. 2.

(A) The competitive abilities of species A–G are ranked at random for three limiting factors. (B) Two possible competitive relationships can emerge: (i) The inferior species is ranked lower than its competitor for all three factors (e.g., C versus B, black arrows) or (ii) the inferior species is ranked lower than its competitor for two factors (e.g., A and B, red arrows). (C) We can use this information to “draw” tournaments: We draw an arrow from node i to j with a probability equal to the proportion of factors for which species i is ranked below j. For example, we draw the arrow A → B with probability 2/3, whereas B → A with probability 1/3. In this way we can generate several tournaments from the same set of competitive relationships in A. For each tournament, we can find the equilibrium solution, and those species with nonzero equilibrium densities coexist (in green), though the equilibrium is neutrally stable.