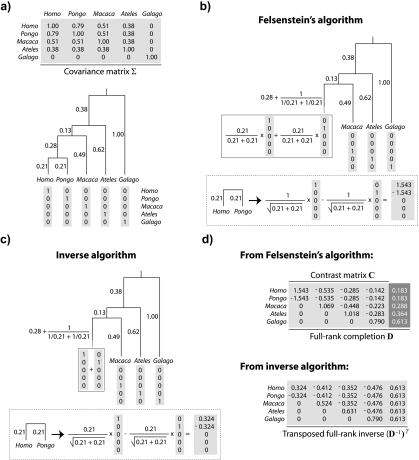
FIGURE 2.

Two algorithmic decompositions of a phylogenetic covariance matrix. a) The phylogeny of Figure 1 and its associated covariance matrix Σ. Each leaf of the tree identifies with a vector chosen from the columns of the identity matrix. b) Matrix representation of Felsenstein's algorithm (Felsenstein 1973, Felsenstein 1985). In each of n − 1 iterations, 2 leaves sharing an immediate common ancestor (e.g., Homo and Pongo) are combined. The consequences of doing so are 3-fold: 1) a contrast is constructed as a weighted difference of the 2 leaf-associated vectors (see the first column of C in panel (d)); 2) a new leaf replaces the combined pair and is identified by a weighted sum of the 2 leaf-associated vectors; and 3) the branch adjacent to the new leaf is lengthened. c) The inverse algorithm. As in b, pruning occurs, resulting in a new leaf whose adjacent branch is lengthened; however, the weighted sums and differences of the 2 vectors comprising the cherry are different and constructed as shown. d) Square roots of C and of its inverse. The contrast vectors from Felsenstein's algorithm form an n×(n − 1) matrix C that satisfies C^TΣC = I_{n − 1}; addition of a final column (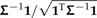, dark gray) yields a nonsingular matrix D that satisfies D^TΣD = I_n. The vectors from the inverse algorithm form an n×n matrix B that is in fact the transposed inverse of D.