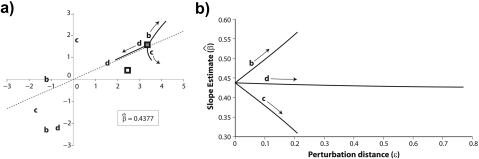
FIGURE 7.

The effect of changing the tree topology on the phylogenetic regression. a) After rooting the trees of Figure 6 arbitrarily on the branch of length 0.13, Felsenstein's algorithm yields 4 independent contrast scores for each of the trees in panels (b–d). The hollow square indicates the Ateles versus Galago contrast that is shared by the 3 topologies and invariant to choice of ε. The filled square indicates the Homo/Pongo/Macaca versus Ateles/Galago contrast that is shared by the 3 topologies but depends on ε. For ε = 0, the contrast scores coincide in transformed coordinate space; as ε increases, the position changes as indicated in by the labeled arrows and curves originating from the filled square (at ε = 0). Each of the trees in panels (b–d) additionally has 2 contrasts that are private to its topology and invariant to ε; the positions of the contrast scores are labeled by their respective panels. The dotted line indicates the phylogenetic regression line (y = 0.4377x) shared by all 3 trees at the multifurcation parameterized by ε = 0. b) The regression fits corresponding to the 3 trees in Figures 6b–d diverge as ε increases. Because the contrast score unique to Figure 6b has an upward trajectory relative to the ε = 0 regression line (see panel (a)), the estimated slope corresponding to that tree is increasing with increasing ε. Likewise, the estimated slope corresponding to the tree in Figure 6c decreases with increasing ε. Panel (a) shows that the trajectory of the contrast score unique to Figure 6d runs nearly parallel to the ε = 0 regression line; because of this, the slope does not change much as ε varies.