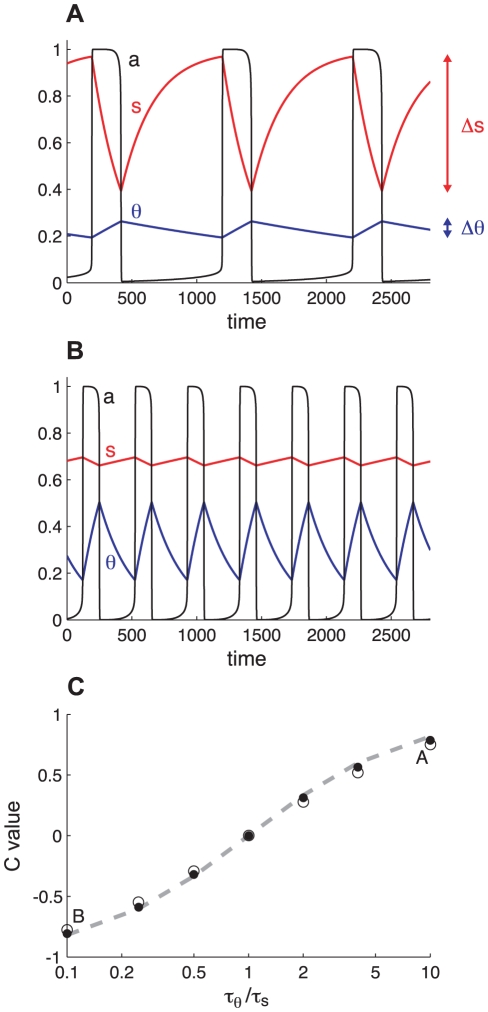
Figure 1. Illustration of the concept that the faster process contributes more to rhythm generation.

A. Time courses of activity (a, black), the synaptic recovery variable (s, red), and the adaptation variable (θ, blue) for τ_θ/τ_s = 10. The range of variation of s (Δs) is about 10 times larger than the range of variation of θ (Δθ). Thus, according to the correlative measure s contributes more to the rhythmicity. B. Similar time courses for τ_θ/τ_s = 0.1. The cellular adaptation now appears to contribute more than the synaptic recovery variable. C. Plot of the variations of C =  (R−1)/(R+1) with the τ_θ/τ_s ratio. Closed circles obtained from simulations with θ₀ = 0; open circles for θ₀ = 0.18. When θ is much faster than s (τ_θ/τ_s is small), C is close to -1 indicating that θ is the dominant process. When τ_θ ≈ τ_s, C≈0 indicating that both processes have equal contribution to the rhythm. At large τ_θ/τ_s, C approaches 1 and s is the dominant process. Points labeled A and B refer to the cases illustrated in panels A and B. Dashed curve, variations of c = (r−1)/(r+1) with τ_θ/τ_s; r = (w/g)(τ_θ/τ_s) and w = g = 1. Results are similar if we keep τ_θ/τ_s = 1 and vary w/g instead.