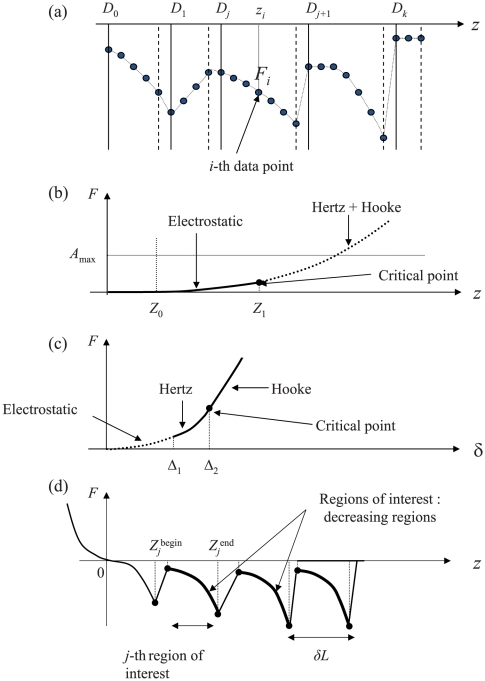
Figure 1. Main notations and schematic illustration for the three steps of the proposed algorithm.
(a) Segmentation of a force curve (first step). The data points (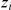 ,
, 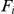 ), i = 1,…,n are partitioned into k+1 contiguous intervals
), i = 1,…,n are partitioned into k+1 contiguous intervals 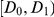 ,
, 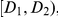 …,
…,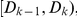
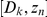 with
with 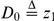 and
and 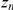 the minimal and maximal
the minimal and maximal 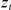 values. The plain and dashed vertical lines represent the left and right bounds of the segmented intervals. The experimental data
values. The plain and dashed vertical lines represent the left and right bounds of the segmented intervals. The experimental data 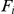 are smoothed on each interval (piecewise smoothing). (b) Detection of the electrostatic region in the
are smoothed on each interval (piecewise smoothing). (b) Detection of the electrostatic region in the  -domain (second step) and fitting to the electrostatic model (third step). The critical points
-domain (second step) and fitting to the electrostatic model (third step). The critical points 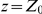 and
and 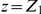 are the edges of electrostatic region in the
are the edges of electrostatic region in the  -domain. A
max is an upper bound for the exponential prefactor A. It is optional but useful for improving the detection of the edge
-domain. A
max is an upper bound for the exponential prefactor A. It is optional but useful for improving the detection of the edge 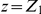 by forbidding
by forbidding  -values that lead to unrealistic values of A. (c) Segmentation and fitting in the δ-domain (third step). The critical points
-values that lead to unrealistic values of A. (c) Segmentation and fitting in the δ-domain (third step). The critical points 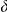 =
= 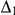 and
and 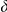 =
= 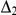 correspond to the beginning of the Hertzian and Hooke regimes, respectively. (d) Retraction curve: the j–th region of interest is the j–th decreasing interval
correspond to the beginning of the Hertzian and Hooke regimes, respectively. (d) Retraction curve: the j–th region of interest is the j–th decreasing interval 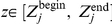 . The search for these regions is done from the outputs of the segmentation algorithm (second step), then the data are fitted to the FJC model within each region of interest (third step).
. The search for these regions is done from the outputs of the segmentation algorithm (second step), then the data are fitted to the FJC model within each region of interest (third step).