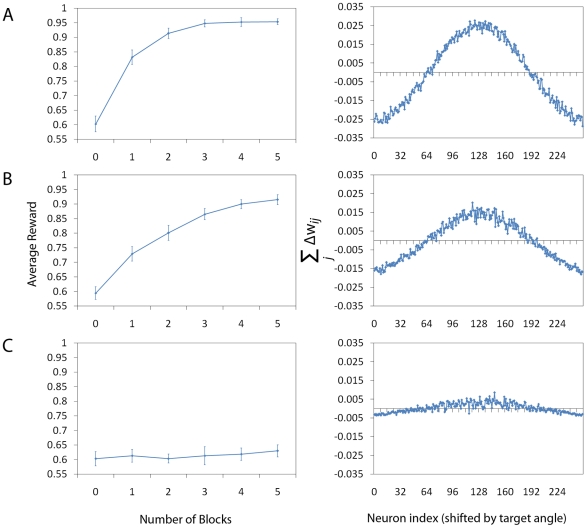
Figure 3. Analysis of System Performance.

Panels A–C (left column) show the average performance of 16 animats calculated in the following way. Every animat completes a number of blocks of 512 trials (the number here varies from 0 to 5), with weights being updated at the end of each trial. We term these “blocks of learning trials”. In these figures, 0 blocks of learning trials means that no learning has taken place. The average reward is calculated independently from the blocks of learning trials. Following a block of learning trials, the animat performs of 128 independent (analysis) trials with learning being disabled, based on which the performance of the system is evaluated (mean reward over a total of 128x16 samples). The parameters for systems A–C are the same as in the previous figure (i.e. A: no lateral connections, B: lateral connections and C: very strong lateral connections). We note that the system without lateral connections achieves 70% of reward twice as fast as the system with lateral connections. The system with strong lateral connections completely fails to learn the task. We can obtain a better understanding of the difference between the three systems by plotting the gradient term for each case correspondingly (Panels A–C, right column). 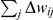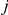We calculate the gradient numerically by summing the value of the potential weight change (before learning where the potential change is maximal) over Place Cell index and by shifting the index of the Action Cell population so that the peak will always appear at the middle of the graph. 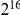To achieve a smooth graph, we average over a total of trials. We note that the gradient is larger when lateral connections are absent.