Retrospective Evaluation of PET-MRI Registration Algorithms

Abstract

The purpose of this study is to evaluate the accuracy of registration positron emission tomography (PET) head images to the MRI-based brain atlas. The [¹⁸F]fluoro-2-deoxyglucose PET images were normalized to the MRI-based brain atlas using nine registration algorithms including objective functions of ratio image uniformity (RIU), normalized mutual information (NMI), and normalized cross correlation (CC) and transformation models of rigid-body, linear, affine, and nonlinear transformations. The accuracy of normalization was evaluated by visual inspection and quantified by the gray matter (GM) concordance between normalized PET images and the brain atlas. The linear and affine registration based on the RIU provided the best GM concordance (average similarity index of 0.71 for both). We also observed that the GM concordances of linear and affine registration were higher than those of the rigid and nonlinear registration among the methods evaluated.

Background

Positron emission tomography (PET) has matured in recent years as a functional imaging modality that provides insight into cell metabolism in health and disease.^1,2 [¹⁸F]Fluoro-2-deoxyglucose (FDG) PET images deliver quantitative data on human brain metabolism.³ Unfortunately, FDG PET data contain little anatomic information. In contrast, magnetic resonance (MR) images provide details of anatomic structure. Therefore, combining PET and MR provides important information on the structure–function relationship and permits precise anatomically based definition of a region of interest.¹ The fusion of PET and MR images can be achieved by using hardware or software, that is, a dedicated system acquiring PET and MR images simultaneously or a computation algorithm fusing PET and MR images that are collected separately. Although the hardware solution provides near-perfect image registration, very few such systems are available in current clinic settings due to the cost and technology limitations. In addition, with the recent development of the multimodality and population-based atlases,⁴ it will be a great benefit to normalize PET information with other information such as cytoarchitectonic probability maps and molecular architectonic maps. The population-averaged standard space based on MR images is generated to allow spatial normalization of multidimensional data; for example, ICBM452 is an averaged brain atlas based on MR images of 452 healthy subjects, and cytoarchitectonic probability maps are currently adding to it (www.loni.ucla.edu/ICBM/). Therefore, registration plays an important role in PET studies.

A computation registration algorithm is typically made up of four components: an objective function, a transformation model, an optimization process, and an interpolation method. The objective function defines the quantitative measure of the spatial agreement between two images. The objective functions establish images' correspondence extrinsically (fiducial localization errors) or intrinsically. The intrinsic correspondences include feature-based methods and intensity-based methods. The representative feature-based objective functions are “head-and-hat”,⁵ the iterative closest point algorithm,⁶ and, recently, wavelet-based attribute vector.⁷ The representative intensity-based objective functions include cross correlation (CC),⁸ square intensity difference,⁹ ratio image uniformity (RIU),^10,11 mutual information,¹² and Kullback–Leibler distance.¹³ The transformation model defines degrees of freedom (DOF) of moving images, including rigid-body registration with 6 DOF (3 translation and 3 rotation), linear registration with 9 DOF (3 scaling plus the 6 DOF of rigid-body registration), affine registration with 12 DOF (3 shearing plus the 9 DOF of linear registration), and nonlinear registration with more than 12 DOF (dependent on transformation models used). Many nonlinear transformation models have been developed. A detailed review of registration objective functions and transformation models can be found in a previous report.¹⁴ The optimization process is a computer search for the extremum of the objective function. The interpolation method is used to resample the source images to the desired image resolution. In this study, we evaluated image fusing algorithms using five well-known registration toolkits. These toolkits use different objective functions and transformation models, and several objective functions and transformation models are implemented in each toolkit. We believe that objective functions and transformation models are the key factors that affect the accuracy of registration. Therefore, we evaluated registration algorithms in terms of objective function/transformation model rather than registration toolkit.

Although almost every registration algorithm is developed with experimental validation results, each validation experiment unfortunately has a unique data set and design. Therefore, independent quantitative and qualitative assessments of registration fidelity are essential for multimodality image fusing.¹⁴ Previous validation studies can be divided into four groups based on the methodology of selection/generation of ground truth: fiducial markers, phantoms, simulated images, or features extracted from images. A brief introduction is provided below with examples of the evaluation of PET-MR registration studies; however, registration evaluation without the involvement of PET-MR registration was not included due to the scope of this study. The first approach to generating the ground truth of registration evaluation is introducing extrinsic markers either by neurosurgery or by attaching them to the skin surface. For example, the “Retrospective Registration Evaluation Project” provided a common evaluation framework based on gold standard PET, computed tomography (CT), and MR images of nine patients undergoing neurosurgery (four fiducial markers on each patient).¹⁵ The disadvantage of validation based on fiducial markers is that markers are spatially sparse and far from the interior brain structures and, thus, do not provide local resolution and accuracy sufficient for validation.¹⁴ An alterative ground truth method is to use a physical phantom with fiducial markers. For example, eight registration algorithms were evaluated using a Hoffman brain phantom filled with ⁹⁹Tc^m (single-photon emission tomography [SPET]) and a phantom filled with water doped with Gd-DTPA.¹⁶ The physical phantom images share the same limitation of spatially sparse markers (four markers were used in a previous study ¹⁶). The third approach to generate ground truth is construction of simulated images with known transformations. For example, two registration algorithms were compared using 192 PET images that were simulated from six MR images.¹⁷ Validations using the features extracted from the images are often used for inter-subject registration of MR images. For example, the manually segmented brain structures have been used to evaluate the different transformation models in registration of MR images in previous reports.^18–20 A selective-wavelet reconstruction technique using a frequency-adaptive wavelet space threshold was also used to compare transformation models for inter-subject MR PET registrations.²¹

The purpose of this study was to evaluate the agreement of the spatial normalized PET images with the MR-based brain atlas using well-accepted registration algorithms. The rationale for this study was based on the following considerations. First, normalization of PET images to the brain atlas will play an important role in interpreting PET results with the development of population-based multimodal brain atlases. However, previous validations were focused on multi-modality registration of images from the same patient or simulated images from the same subject. Secondly, most of the previous comparison studies were focused on rigid-body registration, although it is reasonable to believe that nonlinear registration may not improve the agreement of normalization with consideration of the spatial resolution of PET images. We do expect affine and linear registration to provide better agreement than the previously compared rigid-body registration. In this study, nine registration algorithms with RIU,^10,11,22 normalized mutual information (NMI),¹² and normalized CC objective functions with rigid-body, linear, affine, and nonlinear transformation models were used to normalize head sections of whole-body PET images of 25 patients to the population-based brain atlas ICBM452. These registration algorithms are implemented in registrations toolkits of Automated Image Registration (AIR 5.0);^10,11,22,23 Medical Image Processing, Analysis and Visualization (MIPAV) (mipav.cit.nih.gov); HERMES software (Hermes Medical Solutions, Sweden); and VTK CISG. The gray matter (GM) on normalized PET images was segmented using the fuzzy C-means algorithm²⁴ implemented in MIPAV. The tissue concordance of GM on the normalized PET images and those provided with the atlas were calculated to evaluate the agreement of the spatial normalization.

Methods

Data

The head sections of whole-body FDG PET images of 25 patients treated for malignant lymphoma or Hodgkin's disease were used for the evaluation. The patient group was arbitrarily selected and consisted of 11 girls and 14 boys with a median age of 6.92 years (range, 5.08–9.0 years). The whole-body PET images were acquired for diagnosis purposes on a GE Discovery LS PET-CT scanner with a spatial resolution of 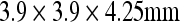(Fig. 1).

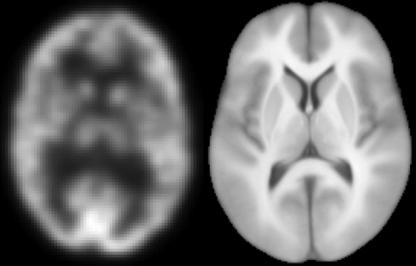
Fig 1.

An illustration of a PET image and the brain atlas used for registration evaluation. Transverse slices near the level of basal ganglia and generally showing the putamen and lateral ventricle were selected for illustration. The left image and the right image are slices from the PET and atlas data, respectively.

The brain atlas, ICBM452 (www.loni.ucla.edu/Atlases/), is a population-based brain atlas averaged from T₁-weighted MR images of 452 healthy young adult brains. The space of the atlas is not based on any single subject but is an average space constructed from the average position, orientation, scale, and shear from all the individual subjects (Fig. 1).

Retrospectively using the above data for this study was approved by the institutional review board at our institution.

Registration Algorithms

Nine registration methods with RIU, NMI, or normalized CC objective functions were evaluated using rigid, linear, affine, and nonlinear transformation models. All registration algorithms were implemented as true 3D registrations. The registration methods were selected on the basis of the knowledge of and availability to the authors. This study focused on objective functions and transformation models. Therefore, we used the optimization search method provided by each registration toolkit, and trilinear interpolation was used for all the registration tests.

Four registration algorithms on the basis of the RIU objective function with rigid, linear, affine, or nonlinear transformation models were evaluated using AIR 5.0.^10,11,22,23 The RIU objective function is a mean-normalized standard deviation of the ratio of the source image intensity to the target image intensity.^22,23 The rigid, linear, and affine models are the standard transformation models as described in “Introduction”. A third-order polynomial with 60 parameters was used for nonlinear registration as recommended by the AIR developer (bishopw.loni.ucla.edu/AIR3/howtosubjects.html). The optimization procedure used in AIR is an iterative, univariate Newton–Raphson search.^22,23

Four registration algorithms on the basis of NMI objective function with rigid, linear, affine, or nonlinear transformation models were evaluated. The NMI objective function is a measure of how well one image explains the other and is calculated as the sum of probability distributions of the source and target images divided by the joint probability distribution of the source and target images.^12,25 We used the NMI-based rigid-body registration implemented in MIPAV (mipav.cit.nih.gov) with the Powell optimization search. The linear registration-based NMI used was implemented in the commercially available HERMES software (Hermes Medical Solutions) with the Powell optimization search. The affine registration used was implemented in SPM2 (www.fil.ion.ucl.ac.uk/spm/software/spm2/) with the Powell optimization search. The free form deformation (FFD) based on NMI implemented in the VTK CISG registration toolkit ²⁶ was used as the nonlinear registration.

One registration algorithm with the normalized CC objective function and the affine transformation model implemented in MIPAV was tested. The normalized CC is a measure of the correlation between the source and target images with the assumption of a linear relationship. It is calculated as the sum of the intensity correlation (normalized by subtracting the mean) between the target and source images divided by the standard deviation.²⁷ The Powell optimization search was used for this registration algorithm.

Evaluation

The agreement of spatial normalization was evaluated qualitatively by visual inspection of normalized PET images overlaid on the brain atlas and quantitatively by calculation of GM tissue concordance between the normalized PET images and the brain atlas. The visual inspection included visual assessment of the agreement of brain surfaces, cerebella, brain stems, and boundaries of corpus callosum and lateral ventricles between the normalized PET images and the brain atlas in orthogonal views.

The normalized PET images were segmented using fuzzy C-means ²⁴ implemented in MIPAV. The fuzzy C-means algorithm is an unsupervised segmentation method based on fuzzy set theory and generalized K-means algorithms. It iteratively minimizes the fuzzy membership function weighted difference between voxel intensity and clusters' centers,

1

in which 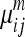is the fuzzy membership function and m can be any number greater than 1 (m = 2 in MIPAV). The iteration stops when the difference between membership functions of all voxels in two consecutive iterations is smaller than the tolerance. The detailed implementation of the algorithm is described in the MIPAV documentation (mipav.cit.nih.gov). The validity of fuzzy C-means segmentation algorithm on PET was reported in previous studies.^24,28 The normalized PET images were segmented into three classes with tolerance of 0.0001 for this study. The GM regions on the atlas were defined as voxels for which GM probability (provided with the atlas) was greater than that of white matter (WM) and cerebrospinal fluid (CSF) on the tissue probability map and greater than 0.5. The tissue concordances of GM between the normalized PET images and atlases were calculated as kappa indices:

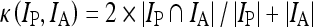2

where I_p and I_A are normalized PET images and the brain atlas, respectively.

Results

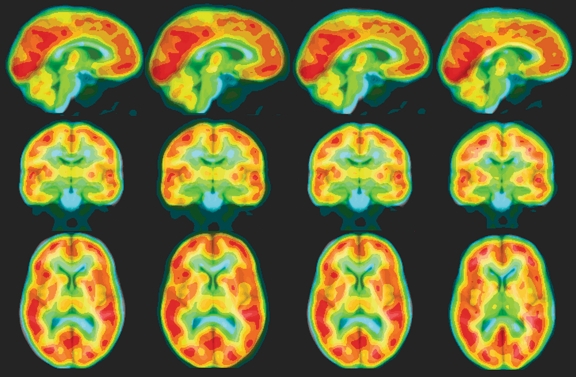
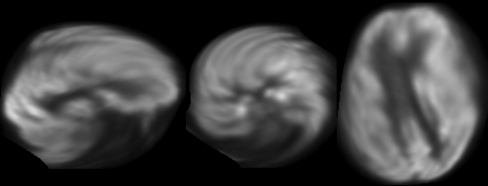
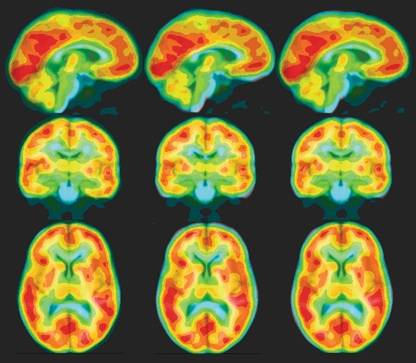
Figure 2 shows a typical normalized PET image overlaid on the atlas using RIU with the four transformation models. Visual inspection of RIU-based transformations showed that the affine registrations provided better agreement of brain surface and matched the low FDG uptakes with the WM and ventricles better than the rigid-body registration did. Visual inspection also showed that normalized PET images from 20 of 25 patients had distorted transformations; thus, we considered that these registrations failed (Fig. 3).

Fig 2.

An example of spatial normalization of a PET image to the MR brain atlas using RIU with various transformation models. The normalized PET image was overlaid onto the brain atlas with blue, green, yellow, and red representing increasing FDG uptake (intensities of PET images). Orthogonal views of the same image are displayed in each column. From left to right, the normalized PET images show rigid-body, linear, affine, and nonlinear transformation models.

Fig 3.

A PET image that was considered a failed normalization with distortion. From left to right, orthogonal (sagittal, coronal, and transverse) views are shown.

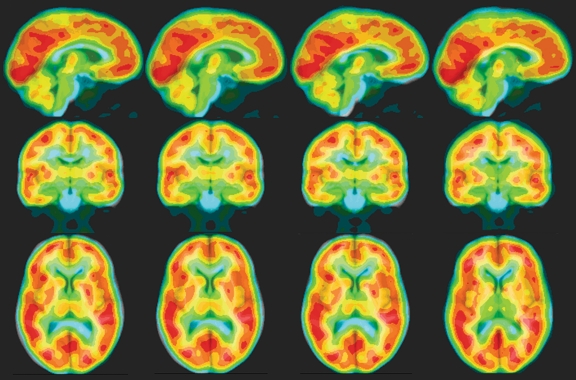
An example of the spatial normalization of PET images to the MR brain atlas using NMI with the four transformation models is shown in Figure 4. Visual inspection showed a similar degree of mismatching among all the transformation models (better brain surface agreement with less agreement of FDG uptake, WM, and CSF or vice versa). However, no distorted normalization was observed in the nonlinear registrations.

Fig 4.

Spatial normalization of PET to the brain atlas using NMI with various transformation models. The normalized PET image was overlaid onto the brain atlas with blue, green, yellow, and red representing increasing FDG uptake (intensities of PET images). Orthogonal views of the same image are displayed in each column. From left to right, the normalized PET images show rigid-body, linear, affine, and nonlinear transformation models.

A comparison of spatial normalization using various objective functions with the affine registration model is shown in Figure 5. Visual inspection showed that spatial normalization using CC and RIU had better agreement of brain surface agreement than those using NMI had and that normalization using RIU matched the low FDG uptake with CSF and WM better than using NMI.

Fig 5.

Comparison of the spatial normalization of PET data to the brain atlas using various objective functions with affine registration. The normalized PET image was overlaid onto the brain atlas with blue, green, yellow, and red representing increasing FDG uptake (intensities of PET images). Orthogonal views of the same image are displayed in each column. From left to right, the images show the CC, RIU, and NMI objective functions.

The GM concordances of the normalized PET images and the brain atlas are summarized in Table 1. The spatial normalization using RIU had the best agreement (averaged kappa index of 0.71) among the objective functions evaluated. The linear and affine registrations had better GM agreement than rigid-body registration (most of the nonlinear registrations failed) using RIU as the objective function.

Table 1.

GM Concordance and Robustness of Registration

Registration	Averaged GM concordance	Standard deviation of the concordance	Robustness (%)
RIU/rigid	0.60	0.06	100
RIU/linear	0.71	0.03	100
RIU/affine	0.71	0.04	100
RIU/nonlinear	–	–	20
NMI/rigid	0.59	0.07	100
NMI/linear	0.59	0.06	100
NMI/affine	0.52	0.04	96
NMI/nonlinear	0.56	0.11	92
CC/affine	0.64	0.04	100

GM concordance was calculated as the kappa index between normalized PET and brain atlas. Robustness was calculated as the percentage of registrations without obvious distortion over the total number of registrations. RIU, NMI, and CC represent the objective functions of RIU, NMI, and CC. “–” designates that the GM concordance was not evaluated or registration was not evaluated

Discussion

The linear and affine registration methods using RIU had the best agreement among the registrations we evaluated. It is well known that registration performance is affected by the level of noise and resolution of image data. Therefore, we used PET data acquired from actual clinical care rather than data generated for research purposes or simulated from MR images for the evaluation. The whole-body PET scans of these patients were acquired for lymphoma or Hodgkin's disease without any sign of central nervous system insult. We used GM concordance as the quantitative measure of spatial normalization because the data were acquired without landmarks. Although previous evaluation studies focused on rigid-body registration, the results of the co-registration portion of our study were consistent with those of previous studies.^15–17,29

The visual inspection was consistent with the measure of GM concordance, although visual inspection cannot produce a conclusive judgment in some cases; for example, there was no visually discerned difference in the comparison of spatial normalization using various objective functions with the affine registration model (Fig. 5). Visual inspection showed that the affine registration model had the best agreement; hence, we used it to evaluate the objective functions. The other objective functions, including count difference, shape difference, sign changes, variance, square root, 2D gradient, and 3D gradient, were compared with RIU in a previous study,¹⁶ and RIU yielded the smallest errors for SPET-MRI registration. Therefore, we did not repeat those comparisons in this study. We used GM concordance as the quantitative metric for evaluation in this study because we believe a “perfect” registration will align the brain tissues together. However, GM concordance could be affected by the segmentation, inherent resolutions, and other factors. We believe that the effect of the accuracy of segmentation on the evaluation process is negligible because there are significant intensity differences (FDG uptakes) between the GM and WM/CSF on PET images. The GM segmentation on the brain atlas is provided with the atlas, averaged from the individual brain images. Therefore, GM concordance can be used as an index for comparison between registration methods. We did not use the WM or CSF concordances because the intensities of WM and CSF are similar on PET images. Although we are not able to ensure that the evaluated algorithms stand for the state-of-art registration methodology, to the best of our knowledge, the software and algorithms evaluated in this study are widely used and well accepted in clinic and research studies.

We found that spatial normalization using RIU had the best agreement of GM concordance among the objective functions tested. Although both RIU and NMI measure the intensity correspondence between two images, RIU segments one image into partitions and maps the other image voxel intensities into each partition, whereas NMI maps two images' intensity distribution with the assumption that the GM intensity on the MR image can be mapped to the GM intensity on the PET image with a similar intensity distribution (not necessarily equivalence of voxel intensity). There is a great difference between GM and WM on FDG PET images, and variations in voxel intensity for each tissue are greater than those with other image modalities such as MR and CT. This feature enables RIU-based registration to more reliably find the global minimum because of the greater weighted sum of standard deviations, although the low resolution and partial volume effect make boundaries on PET images less sharp. We found that linear and affine registrations had better agreement than the rigid-body registration. This was expected for inter-subject registration because of inter-subject size variations. However, we were surprised to find out that registrations with nonlinear transformation models did not yield better or equal agreements than affine registration, considering that nonlinear registration was performed on the affinely normalized images. We think that the possible reason for this is that the limited information resulting from the low resolution of PET images cannot produce a “correct” transformation; that is, the distorted registration does have smaller objective function value although it does not demonstrate better “alignment” than the affine normalization.

There is no consensus on how good is good enough for registration. That determination depends on the purpose of registration and availability of other approaches. The best agreement we obtained in this study was a GM concordance of 0.71 by linear/affine registration based on RIU. We think that it is satisfactory for spatial normalization of PET data to a brain atlas, considering the fact that the GM concordance is calculated on resampled PET and brain atlas images with spatial resolution of , whereas the spatial resolution of the original PET image was 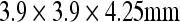. This is in agreement with the conclusions from previous validation studies.^16,17,29,30 Furthermore, there are different brain templates available for various purposes of registration. For example, we believe that the MNI PET template is more appropriate if the purpose of registration is to normalize individual PET image into a common space. We used ICBM452 brain atlas based on MR images because we would like to explore the relationship between FDG uptakes and anatomic structures and cytoarchitectonic structures in the future. For the same reason, we did not normalize the PET data to the pediatric brain template.

There were several limitations to this study. First, whole-body PET scans were used rather than brain PET scans. It is to be expected that the whole-body PET images had higher noise levels and lower resolution than brain-specific images would have had. The whole-body PET data were used based on the availability of normal PET data (with the assumption that head images of the patients with malignant lymphoma or Hodgkin's disease would not be affected by their disease). Second, we tested objective functions and transformation models but not other key factors of the optimization process and interpolation method. Third, the time required for computation of spatial normalization was not evaluated. The second and third limitations were because we used publicly available image-processing toolkits. We did not code algorithms to test the optimization process and interpolation method because these two factors are more standardized than the other two factors.

Conclusion

In summary, we found that either linear or affine registration using RIU as the objective function provides the best GM concordance among the registration methods we tested. The linear and affine registration models generally yield higher GM concordance than rigid and nonlinear models.