Skip to main content
. Author manuscript; available in PMC: 2011 May 11.
Published in final edited form as: Europhys Lett. 2008 Sep 12;83(6):64005p1–64005p6. doi: 10.1209/0295-5075/83/64005

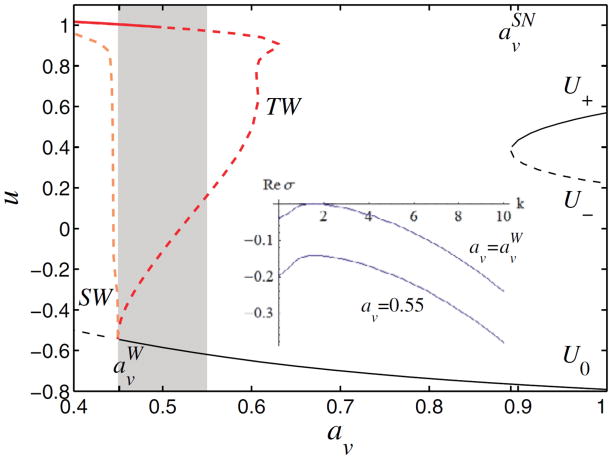
Figure 1.

Figure 1

(Color online) Bifurcation diagram for spatially homogeneous steady (U0, U±, thin black lines) and oscillatory (heavy light colour lines) solutions of eqs. (1). Oscillatory branches of standing waves (SW) and traveling waves (TW) with fixed spatial period λc ≡ 2π/kc ≃ 4.07 are shown in terms of the maximum value umax of u(x, t), and emerge from a finite wave number Hopf bifurcation of U0 ≡ (u0, v0, w0) at av ≡ avW ≃ 0.4497. Solid (dashed) lines indicate stable (unstable) solutions. The shaded region, 0.4497 ≲ av ≲ 0.55, delimits the existence of stable pulse trains of fast type. The inset represents the dispersion relation at onset (av = aWv, kc ≃ 1.54, ωc ≃ 0.4, with TW phase velocity cTWc ≃ 0.26) and near the rightmost limit of the shaded region, av = 0.55, where U0 is linearly stable.