Figure 2.

Interference between Sensory Input and Internally Generated Predictions

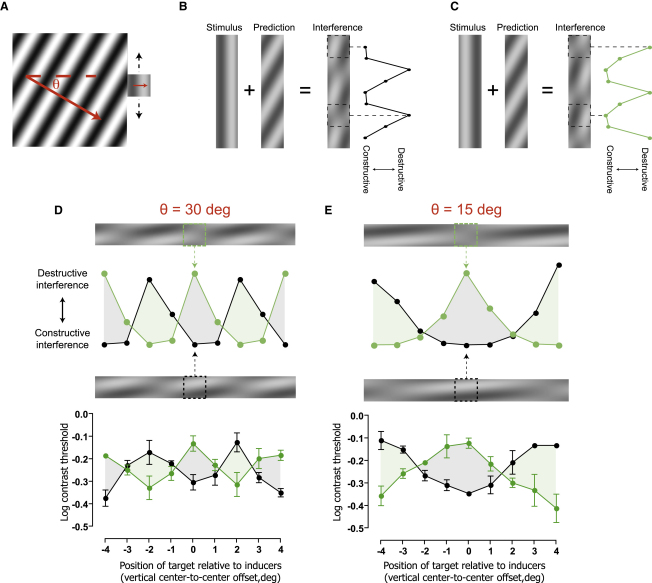
(A) Example of a stimulus configuration in which the drift direction of a large inducer grating has been rotated by 30° relative to a small, rightward-drifting target.

(B) Computation of the theoretical spatial interference profile produced by superposition of the target and a forward model of the inducer. The stimulus panel represents the target at all possible positions along the inducer's edge. Summing this with a prediction formed by extrapolating the inducer pattern results in a spatial interference profile. Locations at which target detectability is expected to benefit from constructive interference are indicated by regions of higher contrast (e.g., upper dashed box), whereas locations at which detectability is expected to be hampered by destructive interference are indicated by lower contrasts (e.g., lower dashed box). Calculating the local contrast in the interference profile at each target location allows an approximation of the expected modulation of target detectability along the edge of the inducer.

(C) Shifting the starting phase of the target by half a cycle, while holding all other factors constant, produces a concomitant shift in the theoretical spatial interference profile.

(D) Comparison of theoretical (upper panel) and empirical (lower panel) spatial interference profiles for an inducer rotated by 30°. Theoretical interference profiles are reproduced from (B) (black symbols) and (C) (green symbols). Mean detection thresholds for three observers are shown, plotted as a function of the target's position relative to the vertical midpoint of the inducer (see Experimental Procedures for details).

(E) Comparison of theoretical (upper panel) and empirical (lower panel) spatial interference profiles for an inducer rotated by 15°. Error bars indicate ± 1 standard error.

See also Figure S2.