Surface Estimation, Variable Selection, and the Nonparametric Oracle Property

Abstract

Variable selection for multivariate nonparametric regression is an important, yet challenging, problem due, in part, to the infinite dimensionality of the function space. An ideal selection procedure should be automatic, stable, easy to use, and have desirable asymptotic properties. In particular, we define a selection procedure to be nonparametric oracle (np-oracle) if it consistently selects the correct subset of predictors and at the same time estimates the smooth surface at the optimal nonparametric rate, as the sample size goes to infinity. In this paper, we propose a model selection procedure for nonparametric models, and explore the conditions under which the new method enjoys the aforementioned properties. Developed in the framework of smoothing spline ANOVA, our estimator is obtained via solving a regularization problem with a novel adaptive penalty on the sum of functional component norms. Theoretical properties of the new estimator are established. Additionally, numerous simulated and real examples further demonstrate that the new approach substantially outperforms other existing methods in the finite sample setting.

1 Introduction

In this paper, we consider the multiple predictor nonparametric regression model y_i = f (x_i) + ε_i, i = 1, …, n, where f is the unknown regression function, x_i = (x_1,i,…, x_p,i) is a p-dimensional vector of predictors, and the ε_i’s are independent noise terms with mean 0 and variances ${\sigma }_i^2$. Many approaches to this problem have been proposed, such as kernel regression (Nadaraya 1964 and others) and locally weighted polynomial regression (LOESS), (Cleveland 1979). See Schimek (2000) for a detailed list of references. When there are multiple predictors, these procedures suffer from the well known curse of dimensionality. Additive models (GAM’s) (Hastie & Tibshirani 1990) avoid some of the problems with high dimensionality and have been shown to be quite useful in cases when the true surface is nearly additive. A generalization of additive modeling is the Smoothing Spline ANOVA (SS-ANOVA) approach (Wahba 1990, Stone, Buja & Hastie 1994, Wahba, Wang, Gu, Klein & Klein 1995, Lin 2000, and Gu 2002). In SS-ANOVA, the function f is decomposed into several orthogonal functional components.

We are interested in the variable selection problem in the context of multiple predictor nonparametric regression. For example, it might be thought that the function f only depends on a subset of the p predictors. Traditionally this problem has been solved in a stepwise or best subset type model selection approach. The MARS procedure (Friedman 1991) and variations thereof (Stone, Hansen, Kooperberg & Truong 1997) build an estimate of f by adding and deleting individual basis functions in a stepwise manner so that the omission of entire variables occurs as a side effect. However, stepwise variable selection is known to be unstable due to its inherent discreteness (Breiman 1995). COmponent Selection Shrinkage Operator (COSSO; Lin & Zhang 2006) performs variable selection via continuous shrinkage in SS-ANOVA models by penalizing the sum of norms of the functional components. Since each of the components are continuously shrunk towards zero, the resulting estimate is more stable than in subset or stepwise regression.

What are the desired properties of a variable selection procedure? For the parametric linear model Fan & Li (2001) discuss the oracle property. A method is said to possess the oracle property if it selects the correct subset of predictors with probability tending to one and estimates the non-zero parameters as efficiently as could be possible if we knew which variables were uninformative ahead of time. Parametric models with the oracle property include Fan & Li (2001) and Zou (2006). In the context of nonparametric regression, we extend the notion of the oracle property. We say a nonparametric regression estimator has the nonparametric (np)-oracle property if it selects the correct subset of predictors with probability tending to one and estimates the regression surface f at the optimal nonparametric rate.

None of the aforementioned nonparametric regression methods have been demonstrated to possess the np-oracle property. In particular, COSSO has a tendency to over-smooth the nonzero functional components in order to set the unimportant functional components to zero. In this paper we propose the adaptive COSSO (ACOSSO) to alleviate this major stumbling block. The intuition behind the ACOSSO is to penalize each component differently so that more flexibility is given to estimate functional components with more trend and/or curvature, while penalizing unimportant components more heavily. Hence it is easier to shrink uninformative components to zero without much degradation to the overall model fit. This is motivated by the adaptive LASSO procedure for linear models of Zou (2006). We explore a special case under which the ACOSSO possesses the np-oracle property. This is the first result of this type for a nonparametric regression estimator. The practical benefit of possessing this property is demonstrated on several real and simulated data examples where the ACOSSO substantially outperforms other existing methods.

In Section 2 we review the necessary literature on smoothing spline ANOVA. The ACOSSO is introduced in Section 3 and its asymptotic properties are presented in Section 4. In Section 5 we discuss the computational details of the estimate. Its superior performance to the COSSO and MARS is demonstrated on simulated data in Section 6 and real data in Section 7. Section 8 concludes. Proofs are given in an appendix.

2 Smoothing Splines and the COSSO

In this section we review only the necessary concepts of SS-ANOVA needed for development. For a more detailed overview of Smoothing Splines and SS-ANOVA see Wahba (1990), Wahba et al. (1995), Schimek (2000), Gu (2002), and Berlinet & Thomas-Agnan (2004).

In the smoothing spline literature it is typically assumed that f ∈ ℱ where ℱ is a reproducing kernel Hilbert space (RKHS). Denote the reproducing kernel (r.k.), inner product, and norm of ℱ as K_ℱ, 〈·, ·〉_ℱ, and ∥ · ∥_ℱ respectively. Often ℱ is chosen to contain only functions with a certain degree of smoothness. For example, functions of one variable are often assumed to belong to the second order Sobolev space, 𝒮² = {g : g, g′ are absolutely continuous and g″ ∈ ℒ²[0, 1]}.

Smoothing spline models are usually assumed without loss of generality to be over x ∈ X = [0, 1]^p. In what is known as smoothing spline (SS)-ANOVA, the space ℱ is constructed by first taking a tensor product of p one dimensional RKHS’s. For example, let ℋ_j be a RKHS on [0, 1] such that ℋ_j = {1} ⊕ ℋ̄_j where {1} is the RKHS consisting of only the constant functions and ℋ̄_j is the RKHS consisting of functions f_j ∈ ℋ_j such that < f_j, 1>_ℋj = 0. The space ℱ can be taken to be the tensor product of the ℋ_j, j = 1,…, p which can be written as

$$ℱ=\underset{j=1}{\overset{p}{\otimes }}{\mathscr{H}}_j=\{1\}\oplus \left\{\underset{j=1}{\overset{p}{\otimes }}{\overline{\mathscr{H}}}_j\right\}\oplus \{\underset{j<k}{\oplus }({\overline{\mathscr{H}}}_j\otimes {\overline{\mathscr{H}}}_k)\}\oplus \cdots .$$ (1)

The right side of the above equation has decomposed ℱ into the constant space, the main effect spaces, the two-way interaction spaces, etc. which gives rise to the name SS-ANOVA. Typically (1) is truncated so that ℱ includes only lower order interactions for better estimation and ease of interpretation. Regardless of the order of the interactions involved, we see that the space ℱ can be written in general as

$$ℱ=\{1\}\oplus \left\{\underset{j=1}{\overset{q}{\oplus }}{ℱ}_j\right\}$$ (2)

where {1},ℱ₁…ℱ_q is an orthogonal decomposition of the space and each of the ℱ_j is itself a RKHS. In this presentation we will focus on two special cases, the additive model $f(\mathit{x})=b+{\displaystyle {\sum }_{j=1}^p{f}_j(x_j)}$ and the two-way interaction model $f(\mathit{x})=b+{\displaystyle {\sum }_{j=1}^p{f}_j(x_j)}+{\displaystyle {\sum }_{j<k}^p{f}_{\mathit{\text{jk}}}(x_j,x_k)}$, where b ∈ {1}, f_j ∈ ℋ̄_j and f_jk ∈ ℋ̄_j ⊗ ℋ̄_k.

A traditional smoothing spline type estimate, f̂, is given by the function f ∈ ℱ that minimizes

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-f({\mathit{x}}_i))}^2+{\mathrm{\lambda }}_0{\displaystyle \sum _{j=1}^q\frac{1}{{\theta }_j}{\parallel P^{j}f\parallel }_{ℱ}^2,}}$$ (3)

where P^j f is the orthogonal projection of f onto ℱ_j, j = 1,…, q which form an orthogonal partition of the space as in (2). We will use the convention 0/0 = 0 so that when θ_j = 0 the minimizer satisfies ∥P^j f∥_ℱ = 0.

The COSSO (Lin & Zhang 2006) penalizes on the sum of the norms instead of the squared norms as in (3) and hence achieves sparse solutions (i.e. some of the functional components are estimated to be exactly zero). Specifically, the COSSO estimate, f̂, is given by the function f ∈ ℱ that minimizes

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-f({\mathit{x}}_i))}^2+\mathrm{\lambda }{\displaystyle \sum _{j=1}^q{\parallel P^{j}f\parallel }_{ℱ}.}}$$ (4)

In Lin & Zhang (2006), ℱ was formed using 𝒮 ² with squared norm

$${\parallel f\parallel }^2={\left({\displaystyle {\int }_0^{1}f(x)\mathit{\text{dx}}}\right)}^2+{\left({\displaystyle {\int }_0^{1}f\prime (x)\mathit{\text{dx}}}\right)}^2+{\displaystyle {\int }_0^1{(f″(x))}^2\mathit{\text{dx}}}$$ (5)

for each of the ℋ_j of (1). The reproducing kernel can be found in Wahba (1990).

3 An Adaptive Proposal

Although the COSSO is a significant improvement over classical stepwise procedures, it tends to oversmooth functional components. This seemingly prevents COSSO from achieving a nonparametric version of the oracle property (defined in Section 4). To alleviate this problem, we propose an adaptive approach. The proposed adaptive COSSO uses individually weighted norms to smooth each of the components. Specifically we select as our estimate the function f ∈ ℱ that minimizes

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-f({\mathit{x}}_i))}^2+\mathrm{\lambda }{\displaystyle \sum _{j=1}^q{w}_j{\parallel P^{j}f\parallel }_{ℱ}.}}$$ (6)

where the 0 < w_j ≤ ∞ are weights that can depend on an initial estimate of f which we denote f̃. For example we could initially estimate f via the traditional smoothing spline of (3) with all θ_j = 1 and λ₀ chosen by the generalized cross validation (GCV) criterion (Craven & Wahba 1979). Note that there is only one tuning parameter, λ, in (6). The w_j’s are not tuning parameters like the θ_j’s in (3), rather they are weights to be estimated from the data in a manner described below.

3.1 Choosing the Adaptive Weights, w_j

Given an initial estimate f̃, we wish to construct w_j’s so that the prominent functional components enjoy the benefit of a smaller penalty relative to less important functional components. In contrast to the linear model, there is no single coefficient, or set of coefficients, to measure importance of a variable. One possible scheme would be to make use of the L₂ norm of P^j f̃ given by ∥P^j f̃∥_L2 = (∫_X(P^j f̃(x))²dx)^1/2. For a reasonable initial estimator, this quantity will be a consistent estimate of ${\parallel P^{j}f\parallel }_{L_2}^2$ which is often used to quantify the importance of functional components. This would suggest using

$$w_j={\parallel P^j\tilde{f}\parallel }_{L_2}^{-\gamma }.$$ (7)

In Section 4, the use of these weights results in favorable theoretical properties.

There are other reasonable possibilities one could consider for the w_j ’s. In fact at first glance, as an extension of the adaptive LASSO for linear models, it may seem more natural to make use of an estimate of the RKHS norm used in the COSSO penalty and set $w_j={\parallel P^j\tilde{f}\parallel }_{ℱ}^{-\gamma }$. However, the use of these weights is not recommended because they do not provide an estimator with sound theoretical properties. Consider for example building an additive model using RKHS’s with norm given by (5). Then this w_j is essentially requiring estimation of the functionals ${\displaystyle {\int }_0^1{(f_j^{″}(x_j))}^2{\mathit{\text{dx}}}_j}$ which is known to be a harder problem (requiring more smoothness assumptions) than estimating ${\displaystyle {\int }_0^1{f}_j^2(x)\mathit{\text{dx}}}$ (Efromovich & Samarov 2000). In fact, using $w_j={\parallel P^j\tilde{f}\parallel }_{ℱ}^{-\gamma }$ instead of (7) would at the very least require stronger smoothness assumptions about the underlying function f in Section 4 to achieve asymptotically correct variable selection. Because of this and the results of preliminary empirical studies we recommend the use of the weights in (7) instead.

4 Asymptotic Properties

In this section we demonstrate the desirable asymptotic properties of the ACOSSO. In particular, we show that the ACOSSO possesses a nonparametric analog of the oracle property. This result is the first of its type for nonparametric surface estimation.

Throughout this section we assume the true regression model is y_i = f₀ (x_i) + ε_i, i = 1,…, n. The regression function f₀ ∈ ℱ is additive in the predictors so that ℱ = {1} ⊕ ℱ₁ ⊕⋯⊕ ℱ_p where each ℱ_j is a space of functions corresponding to x_j . We assume that ε_i are independent with Eε_i = 0 and are uniformly sub-Gaussian. Following van de Geer (2000), we define a sequence of random variables to be uniformly sub-Gaussian if there exists some K > 0 and C > 0 such that

$$\underset{n}{\text{sup}}\underset{i=1,\dots ,n}{\text{max}}E[\text{exp}({\epsilon }_i^2/K)]\le C.$$ (8)

Let 𝒮² denote the RKHS of second order Sobolev space endowed with the norm in (5) with 𝒮² = {1} ⊕ 𝒮̄². Also, define the squared norm of a function at the design points as ${\parallel f\parallel }_n^2=1/n{\displaystyle {\sum }_{i=1}^n{f}^2({\mathit{x}}_i)}$. Let U be the set of indexes for all uninformative functional components in the model $f_0=b+{\displaystyle {\sum }_{j=1}^p{P}^j{f}_0,j=1,\dots ,p}$. That is U = {j : P^j f₀ ≡ 0}.

Theorem 1 below states the convergence rate of ACOSSO when used to estimate an additive model. Corollary 1 following Theorem 1 states that the weights given by (7) lead to an estimator with optimal convergence rate of n^−2/5. We sometimes write w_j and λ as w_j,n and λ_n respectively to explicitly denote the dependence on n. We also use the notation X_n ~ Y_n to mean X_n/Y_n = O_p(1) and Y_n/X_n = O_p(1) for some sequences X_n and Y_n. The proofs of Theorem 1 and the other results in this section are deferred to the appendix.

Theorem 1. (Convergence Rate)

Assume that $f_0\in ℱ=\{1\}\oplus {\overline{𝒮}}_1^2\oplus \cdots \oplus {\overline{𝒮}}_p^2\mathit{\text{where}}{\overline{𝒮}}_j^2$ is the space 𝒮̄² corresponding to the j^th input variable, x_j. Also assume that ε_i are independent and satisfy (8). Consider the ACOSSO estimate, f̂, defined in (6). Suppose that $w_{j,n}^{-1}=O_p(1)$ for j = 1,…, p and further that w_j,n = O_p(1) for j ∈ U^c. Also assume that ${\mathrm{\lambda }}_n^{-1}=O_p(n^{4/5})$. If

1. P^j f₀ ≠ 0 for some j, then ${\parallel \widehat{f}-f_0\parallel }_n=O_p({\mathrm{\lambda }}^{1/2}{w}_{*,n}^{1/2})$ where w_*,n = min {w_1,n,…,w_p,n}.

2. P^j f₀ = 0 for all j, then ${\parallel \widehat{f}-f_0\parallel }_n=O_p(\text{max}\{n^{-1/2},n^{-2/3}{\mathrm{\lambda }}^{-1/3}{w}_{*,n}^{-1/3}\})$.

Corollary 1. (Optimal Convergence of ACOSSO)

Assume that $f_0\in ℱ=\{1\}\oplus {\overline{𝒮}}_1^2\oplus \cdots \oplus {\overline{𝒮}}_p^2$ and that ε_i are independent and satisfy (8). Consider the ACOSSO estimate, f̂, with weights, $w_{j,n}={\parallel P^j\tilde{f}\parallel }_{L_2}^{-\gamma }$, for f̃ given by the traditional smoothing spline (3) with θ = 1_p and λ_0,n ~ n^−4/5. If γ > 3/4 and λ_n ~ n^−4/5, then ∥f̂ − f₀∥_n = O_p(n^−2/5) if P^j f₀ ≠ 0 for some j and ∥f̂ − f₀∥_n = O_p(n^−1/2) otherwise.

We now turn to discuss the attractive properties of the ACOSSO in terms of model selection. In Theorem 2 and Corollary 2 we will consider functions in the second order Sobolev space of periodic functions denoted ${𝒮}_{\text{per}}^2\text{where}{𝒮}_{\text{per}}^2=\{1\}\oplus {\overline{𝒮}}_{\text{per}}^2$. We also assume that the observations come from a tensor product design. That is, the design points are ${{\{x_{1,i_1},x_{2,i_2},\dots ,x_{p,i_p}\}}_{i_j=1}^m}_{j=1}^p$ where x_j,k = k/m, k = 1,…,m, j = 1,…, p. Therefore the total sample size is n = m^p. These assumptions were also used by Lin & Zhang (2006) to examine the model selection properties of the COSSO.

Theorem 2. (Selection Consistency)

Assume a tensor product design and $f_0\in ℱ=\{1\}\oplus {\overline{𝒮}}_{\mathit{\text{per}},1}^2\oplus \cdots \oplus {\overline{𝒮}}_{\mathit{\text{per}},p}^2\mathit{\text{where}}{\overline{𝒮}}_{\text{per},j}^2\mathit{\text{is the space}}{\overline{𝒮}}_{\text{per}}^2$ corresponding to the j^th input variable, x_j. Also assume that ε_i are independent and satisfy (8). The ACOSSO estimate f̂ will be such that P^j f̂ ≡ 0 for all j ∈ U with probability tending to one if and only if $n{w}_{j,n}^2{\mathrm{\lambda }}_n^2\stackrel{p}{\to }\infty$ as n → for all j ∈ U.

We will say a nonparametric regression estimator, f̂, has the nonparametric (np)-oracle property if ∥f̂ − f₀∥_n → 0 at the optimal rate while also setting P^j f̂ ≡ 0 for all j ∈ U with probability tending to one. This means that the error associated with surface estimation has the same order as that for any other optimal estimator. One could also define a strong np-oracle property which would require asymptotically correct variable selection and the error being asymptotically the same as an oracle estimator (an estimator where the correct variables were known in advance). That is, to possess the strong np-oracle property, the proposed estimator must match the constant as well as the rate of an oracle estimator. The strong np-oracle definition is slightly ambiguous however, as one must specify what estimator should be used as the oracle estimator for comparison (e.g., smoothing spline with one λ, smoothing spline with differing λ_j’s, etc.). The weaker version of the np-oracle property, which was stated first, avoids this dilemma. The corollary below states that the ACOSSO with weights given by (7) has the np-oracle property.

Corollary 2. (Nonparametric Oracle Property)

Assume a tensor product design and f₀ ∈ ℱ where $ℱ=\{1\}\oplus {\overline{𝒮}}_{\mathit{\text{per}},1}^2\oplus \cdots \oplus {\overline{𝒮}}_{\mathit{\text{per}},p}^2$ and that ε_i are independent and satisfy (8). Define weights, $w_{j,n}={\parallel P^j\tilde{f}\parallel }_{L_2}^{-\gamma }$, for f̃ given by the traditional smoothing spline with λ₀ ~ n^−4/5, and γ > 3/4. If also λ_n ~ n^−4/5, then the ACOSSO estimator has the np-oracle property.

Remark 1

The derivation of the variable selection properties of adaptive COSSO requires detailed investigation on the eigen-properties of the reproducing kernel, which is generally intractable. However, Theorem 2 and the Corollary 2 assume that f belongs to the class of periodic functions while x is a tensor product design. This makes the derivation more tractable, since the eigenfunctions and eigenvalues of the associated reproducing kernel have a particularly simple form. Results for this specific design are often instructive for general cases, as suggested in Wahba (1990). We conjecture that the selection consistency of the adaptive COSSO also holds more generally, and this is also supported by numerical results in Section 6. The derivation of variable selection properties in the general case is a technically difficult problem which is worthy of future investigation. Neither the tensor product design nor the periodic functions assumptions are required for establishing the MSE consistency of the adaptive COSSO estimator in Theorem 1 and Corollary 1.

Remark 2

The COSSO (which is the ACOSSO with w_j,n = 1 for all j and n) does not appear to enjoy the np-oracle property. Notice that by Theorem 2, λ_n must go to zero slower than n^−1/2 in order to achieve asymptotically correct variable selection. However, even if λ_n is as small as λ_n = n^−1/2, Theorem 1 implies that the convergence rate is O_p(n^−1/4) which is not optimal. These results are not surprising given that the linear model can be obtained as a special case of ACOSSO by using $ℱ=\{f:f={\beta }_0+{\displaystyle {\sum }_{j=1}^p{\beta }_j(x_j-1/2)}\}$. For this ℱ the COSSO reduces to the LASSO which is known to be unable to achieve the oracle property (Knight & Fu 2000, Zou 2006). In contrast, the ACOSSO reduces to the adaptive LASSO (Zou 2006) which is well known to achieve the oracle property.

Remark 3

The distribution of the error terms ε_i in Theorems 1 and 2 need only be independent with sub-Gaussian tails (8). The common assumption that ${\epsilon }_i\stackrel{\mathit{\text{iid}}}{~}𝒩(0,{\sigma }^2)$ satisfies (8). But, the distributions need not be Gaussian and further need not even be the same for each of the ε_i. In particular, this allows for heteroskedastic errors.

Remark 4

Theorems 1 and 2 are assuming an additive model, in which case functional component selection is equivalent to variable selection. In higher order interaction models, the main effect for x_j and all of the interaction functional components involving x_j must be set to zero in order to eliminate x_j from the model and achieve true variable selection. Thus, in some other areas of the paper, when interactions are involved, we use the term variable selection to refer to functional component selection.

5 Computation

Since the ACOSSO in (6) may be viewed as the COSSO in (4) with an “adaptive” RKHS, the computation proceeds in a similar manner as that for the COSSO. We first present an equivalent formulation of the ACOSSO, then describe how to minimize this equivalent formulation for a fixed value of the tuning parameter. Discussion of tuning parameter selection is delayed until Section 5.3.

5.1 Equivalent Formulation

Consider the problem of finding θ = (θ₁,…, θ_q)′ and f ∈ ℱ to minimize

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{[y_i-f({\mathit{x}}_i)]}^2+{\mathrm{\lambda }}_0{\displaystyle \sum _{j=1}^q{\theta }_j^{-1}{w}_j^{2-\vartheta }{\parallel P^{j}f\parallel }_{ℱ}^2+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^q{w}_j^{\vartheta }{\theta }_j,\text{subject to}{\theta }_j}\ge 0{\forall }_j,}}$$ (9)

where 0 ≤ ϑ ≤ 2, λ₀ > 0 is a fixed constant, and λ₁ > 0 is a smoothing parameter. The following Lemma says that the above optimization problem is equivalent to (6). This has important implications for computation since (9) is easier to solve.

Lemma 1

Set λ₁ = λ²/(4λ₀). (i) If f̂ minimizes (6), $\mathit{\text{set}}{\widehat{\theta }}_j={\mathrm{\lambda }}_0^{1/2}{\mathrm{\lambda }}_1^{-1/2}{w}_j^{1-\vartheta }{\parallel P^j\widehat{f}\parallel }_{ℱ},$ j = 1,…, q, then the pair (θ̂, f̂) minimizes (9). (ii) On the other hand, if a pair (θ̂, f̂) minimizes (9), then f̂ minimizes (6).

5.2 Computational Algorithm

The equivalent form in (9) gives a class of equivalent problems for ϑ ∈ [0, 2]. For simplicity we will consider the case ϑ = 0 since the ACOSSO can be then viewed as having the same equivalent form as the COSSO with an adaptive RKHS. For a given value of θ = (θ₁,…, θ_q)′, the minimizer of (9) is the smoothing spline of (3) with θ_j replaced by $w_j^{-2}{\theta }_j$. Hence it is known (Wahba 1990 for example) that the solution has the form $f(\mathit{x})=b+{\displaystyle {\sum }_{i=1}^n{c}_i{K}_{\mathit{w},\mathit{\theta }}(\mathit{x},{\mathit{x}}_i)}$ where c ∈ ℜⁿ, b ∈ ℜ and $K_{\mathit{w},\mathit{\theta }}={\displaystyle {\sum }_{j=1}^q({\theta }_j/w_j^2)K_{{ℱ}_j}}$, with ℱ_j corresponding to the decomposition in (2).

Let K_j be the n × n matrix ${\{K_{{ℱ}_j}({\mathit{x}}_i,{\mathit{x}}_j)\}}_{i,j=1}^n$ and let 1_n be the column vector consisting of n ones. Then write the vector f = (f(x₁),…,f(x_n))′ as $\mathit{f}=b{\mathbf{1}}_n+({\displaystyle {\sum }_{j=1}^q({\theta }_j/w_j^2){\mathit{K}}_j})\mathit{c},$, y = (y₁,…,y_n)′ and define ${\parallel \mathit{\upsilon }\parallel }_n^2=1/n{\displaystyle {\sum }_{i=1}^n{\upsilon }_i^2}$ for a vector υ of length n and y = (y₁,…, y_n)′. Now, for fixed θ, minimizing (9) is equivalent to

$$\underset{b,c}{\text{min}}\{\frac{1}{n}{\parallel \mathit{y}-b{\mathbf{1}}_n-{\displaystyle \sum _{j=1}^q{\theta }_j{w}_j^{-2}{\mathit{K}}_j\mathit{c}}\parallel }_n^2+{\lambda }_0{\displaystyle \sum _{j=1}^q{\theta }_j{w}_j^{-2}\mathit{c}\prime {\mathit{K}}_j\mathit{c}}\}$$ (10)

which is just the traditional smoothing spline problem in Wahba (1990). On the other hand if b and c were fixed, the θ that minimizes (9) is the same as the solution to

$$\underset{\mathit{\theta }}{\text{min}}\{{\parallel \mathit{z}-\mathit{G}\mathit{\theta }\parallel }_n^2+n{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^q{\theta }_j}\},\text{subject to}{\theta }_j\ge 0{\forall }_j,$$ (11)

where ${\mathit{g}}_j=w_j^{-2}{\mathit{K}}_j\mathit{c},$, G is the n × p matrix with the j^th column being g_j and z = y − b1_n − (n/2)λ₀c. Notice that (11) is equivalent to

$$\underset{\mathit{\theta }}{\text{min}}{\parallel \mathit{z}-\mathit{G}\mathit{\theta }\parallel }_n^2\text{\hspace{1em}subject to}{\theta }_j\ge 0{\forall }_j\text{and}{\displaystyle \sum _{j=1}^q{\theta }_j}\le M,$$ (12)

for some M > 0. The formulation in (12) is a quadratic programming problem with linear constraints for which there exists many algorithms to find the solution (see Goldfarb & Idnani 1982 for example). A reasonable scheme is then to iterate between (10) and (12). In each iteration (9) is decreased. We have observed that after the second iteration the change between iterations is small and decreases slowly.

5.3 Selecting the Tuning Parameter

In (9) there is really only one tuning parameter, λ₁ or equivalently M of (12). Changing the value of λ₀ will only scale shift the value of M being used so λ₀ can be fixed at any positive value. Therefore, we choose to initially fix θ = 1_q and find λ₀ to minimize the GCV score of the smoothing spline problem in (10). This has the effect of placing the θ_j’s on a scale so that M roughly translates into the number of non-zero components. Hence, it seems reasonable to tune M on [0, 2q] for example.

We will use 5-fold cross validation (5CV) in the examples of the subsequent sections to tune M. However, we also found that the BIC criterion (Schwarz 1978) was quite useful for selecting M. We approximate the effective degrees of freedom, ν, by ν = tr(S) where S is the weight matrix corresponding to the smoothing spline fit with θ = θ̂. This type of approximation gives an under-estimate of the actual df, but has been demonstrated to be useful (Tibshirani 1996). We have found that the ACOSSO with 5CV tends to over select non-zero components just as Zou, Hastie & Tibshirani (2007) found that AIC-type criteria over select non-zero coefficients in the LASSO. They recommend using BIC with the LASSO when the goal is variable selection as do we for the ACOSSO.

6 Simulated Data Results

In this section we study the empirical performance of the ACOSSO estimate and compare it to several other existing methods. We display the results of four different versions of the ACOSSO. All versions use weights w_j given by (7) with γ = 2 since we found that γ = 2 produced the best overall results among γ ∈ {1.0, 1.5, 2.0, 2.5, 3.0}. The initial estimate, f̃, is either the traditional smoothing spline or the COSSO with λ selected by GCV. We also use either 5CV or BIC to tune M. Hence the four versions of ACOSSO are ACOSSO-5CV-T, ACOSSO-5CV-C, ACOSSO-BIC-T, and ACOSSO-BIC-C where (−T) and (−C) stand for using the traditional smoothing spline and COSSO respectively for the initial estimate.

We include the methods COSSO, MARS, stepwise GAM, Random Forest (Breiman 2001), and the Gradient Boosting Method (GBM) (Friedman 2001). The tuning parameter for COSSO is chosen via 5CV. To fit MARS models we have used the ’polymars’ procedure in the R-package ’polspline’. Stepwise GAM, Random Forest, and GBM fits were obtained using the R-packages ’gam’, ’randomForest’, and ’gbm’ respectively. All input parameters for these methods such as gcv for MARS, n.trees for GBM, etc. were appropriately set to give the best results on these examples.

Note that Random Forest and GBM are both black box prediction machines. That is they produce function estimates that are difficult to interpret and they are not intended for variable selection. They are however well known for making accurate predictions. Thus, they are included here to demonstrate the utility of the ACOSSO even in situations where prediction is the only goal.

We also include the results of the traditional smoothing spline of (3) when fit with only the informative variables. That is, we set θ_j = 0 if P^j f = 0 and θ_j = 1 otherwise, then choose λ₀ by GCV. This will be referred to as the ORACLE estimator. Notice that the ORACLE estimator is only available in simulations where we know ahead of time which variables are informative. Though the ORACLE cannot be used in practice, it is useful to display its results here because it gives us a baseline for the best estimation risk we could hope to achieve with the other methods.

Performance is measured in terms of estimation risk and model selection. Specifically, the variables defined in Table 1 will be used to compare the different methods. We first present a very simple example to highlight the benefit of using the ACOSSO. We then repeat the same examples used in the COSSO paper to offer a direct comparison on examples where the COSSO is known to perform well. The only difference is that we have increased the noise level to make these problems a bit more challenging.

Table 1.

Definitions of the variables R̂, ᾱ, 1 − β̄, and model size used to summarize the results of the simulations.

R̂	is a monte carlo estimate of the estimation risk, R(f̂) = E{f̂(X) − f(X)}2. Specifically, let the integrated squared error for a fixed estimate f̂ be given by ISE = EX{f(X) − f̂(X)}2. The ISE is calculated for each realization via a monte carlo integration with 1000 points. The quantity R̂ is then the average of the ISE values over the N = 100 realizations.
ᾱ	is a monte carlo estimate of the type I error rate averaged over all of the uninformative functional components. Specifically, let α̂j be the proportion of realizations that Pj f̂ ≠ 0, j = 1,…, q. Then ᾱ = 1/|U|∑j∈U α̂j where U = {j : Pj f ≡ 0} and |U| is the number of elements in U.
1 − β̄	is a monte carlo estimate of the variable selection power averaged over all of the informative functional components. Specifically, let β̂j be the proportion of realizations that Pj f̂ = 0, j = 1,…, q. Then β̄ = 1/|Uc|∑j∈Uc β̂j where Uc is the complement of U.
model size	is the number of functional components included in the model averged over the N = 100 realizations.

Example 1. The following four functions on [0, 1] are used as building blocks of regression functions in the following simulations:

$$g_1(t)=t;g_2(t)={(2t-1)}^2;g_3(t)=\frac{\text{sin}(2\pi t)}{2-\text{sin}(2\pi t)};$$

$$g_4(t)=0.1\text{sin}(2\pi t)+0.2\text{cos}(2\pi t)+0.3{\text{sin}}^2(2\pi t)+0.4{\text{cos}}^3(2\pi t)+0.5{\text{sin}}^3(2\pi t).$$ (13)

In this example, we let X ∈ ℜ¹⁰. We observe n = 100 observations from the model y = f (X) + ε where the underlying regression function is additive,

$$f(\mathit{x})=5g_1(x_1)+3g_2(x_2)+4g_3(x_3)+6g_4(x_4)$$

and $\epsilon \stackrel{\mathit{\text{iid}}}{~}𝒩(0,3.03)$. Therefore X₅,…,X₁₀ are uninformative. We first consider the case where X is uniform in [0, 1]¹⁰ in which case the signal to noise ratio (SNR) is 3:1 (here we have adopted the variance definition for signal to noise ratio, SNR = [Var( f(X))]/σ²). For comparison, the variances of the functional components are Var{5g₁(X₁)} = 2.08, Var{3g₂(X₂)} = 0.80, Var{4g₃(X₃)} = 3.30 and Var{6g₄(X₄)} = 9.45.

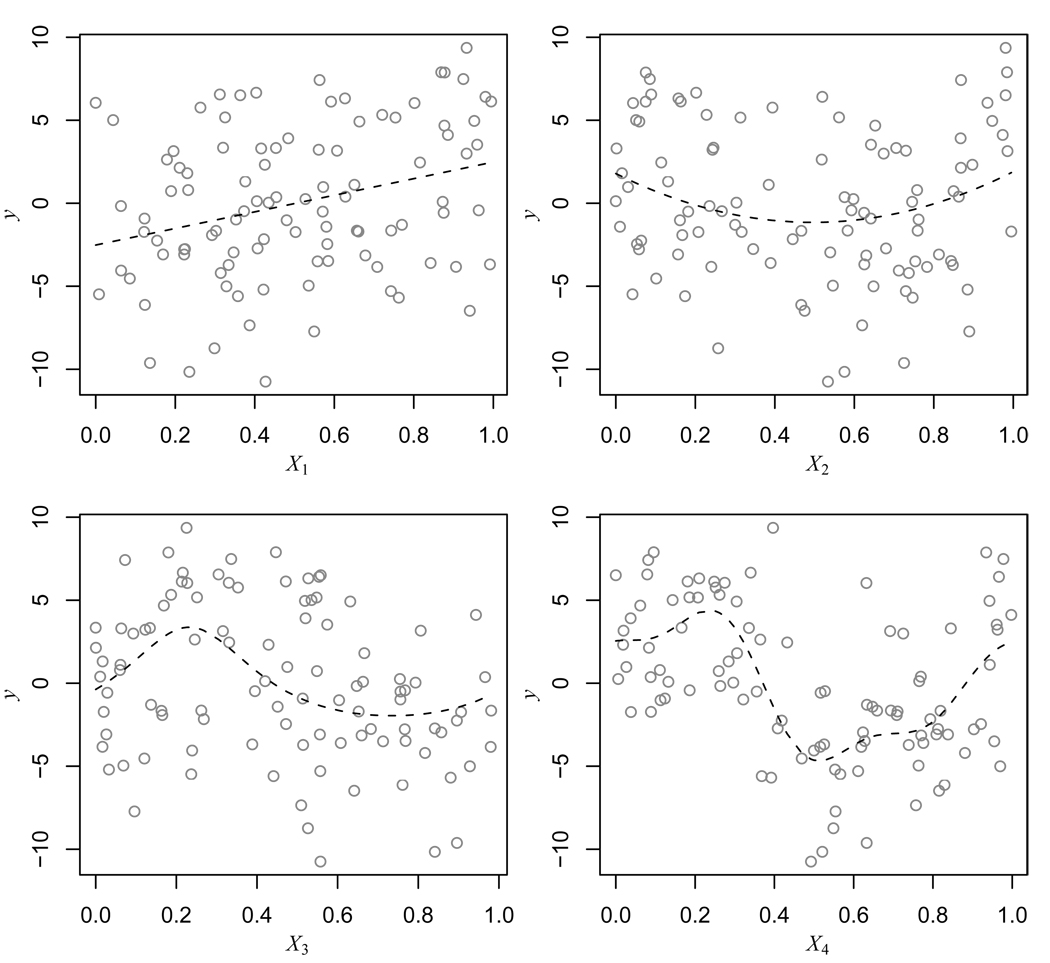
For the purposes of estimation in the methods ACOSSO, COSSO, MARS, and GBM, we restrict f̂ to be a strictly additive function. The Random Forest function however does not have an option for this. Hence there are 10 functional components that are considered for inclusion in the ACOSSO model. Figure 1 gives plots of y versus the the first four variables x₁,…, x₄ along with the true P^j f component curves for a realization from Example 1. The true component curves, j = 1,…,4, along with the estimates given by ACOSSO-5CV-T and COSSO are then shown in Figure 2 without the data for added clarity. Notice that the ACOSSO captures more of the features of the P³ f component and particularly the P⁴ f component since the reduced penalty on these components allows it more curvature. In addition, since the weights more easily allow for curvature on components that need it, M does not need to be large (relatively) to allow a good fit to components like P³ f and P⁴ f. This has the effect that that components with less curvature, like the straight line P¹ f, can also estimated more accurately by ACOSSO than by COSSO, as seen in Figure 2.

Figure 1.

Plot of the true functional components, P^j f, j = 1,…, 4 along with the data for a realization from Example 1.

Figure 2.

Plot of P^j f, j = 1,…, 4 along with their estimates given by ACOSSO, COSSO, and MARS for a realization from Example 1.

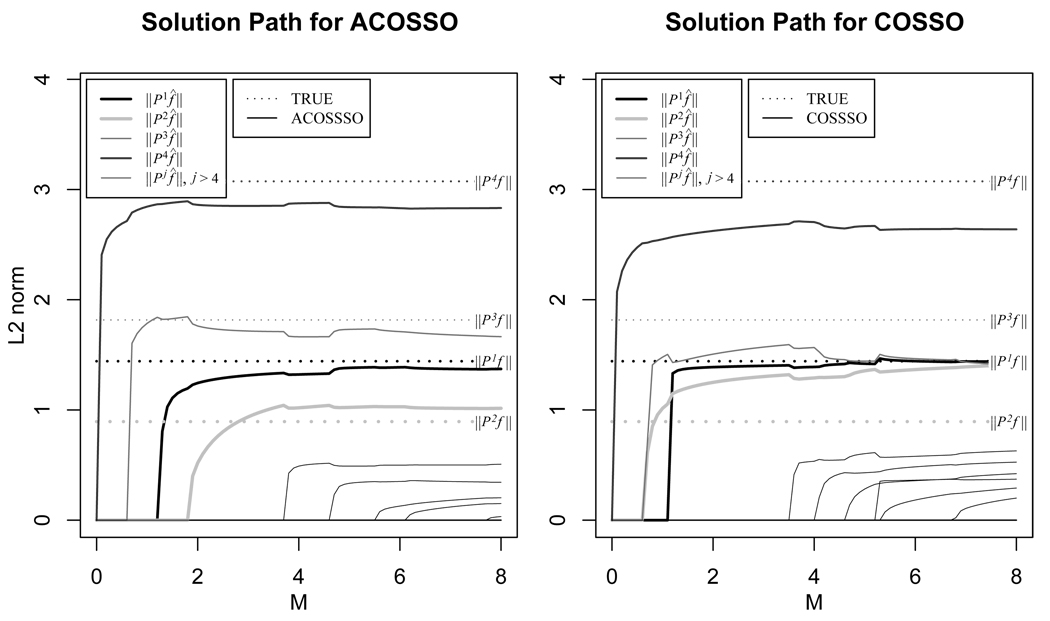
Figure 6 shows how the magnitudes of the estimated components change with the tuning parameter M for both the COSSO and ACOSSO for the above realization. The magnitudes of the estimated components are measured by their L₂ norm ∥P^j f̂∥_L2. Dashed lines are drawn at the true values of ∥P^j f∥_L2 for reference. Notice that estimated functional component norms given by ACOSSO are closer to the true values than those given by the COSSO in general. Also, the uninformative components are more heavily penalized in the ACOSSO making it harder for them to enter the model.

Incidentally using GCV or 5CV for tuning parameter selection for the ACOSSO on the above realization gives M = 3.81 and M = 4.54 respectively, both resulting in a model of 5 functional components for this run. The BIC method however gives M = 2.97, which results in the correct model of 4 functional components. This is a typical occurrence for realizations from this example as can be seen in Table 2.

Table 2.

Results of 100 Realizations from Example 1 in the Uniform Case. The standard error for each of the summary statistics is given in parantheses.

	R̂	ᾱ	1 − β̄	model size
ACOSSO-5CV-T	1.204 (0.042)	0.252 (0.034)	0.972 (0.008)	5.4 (0.21)
ACOSSO-5CV-C	1.186 (0.048)	0.117 (0.017)	0.978 (0.007)	4.6 (0.11)
ACOSSO-BIC-T	1.257 (0.048)	0.032 (0.008)	0.912 (0.012)	3.8 (0.08)
ACOSSO-BIC-C	1.246 (0.064)	0.018 (0.006)	0.908 (0.014)	3.7 (0.07)
COSSO	1.523 (0.058)	0.095 (0.023)	0.935 (0.012)	4.3 (0.15)
MARS	2.057 (0.064)	0.050 (0.010)	0.848 (0.013)	3.7 (0.08)
GAM	1.743 (0.053)	0.197 (0.019)	0.805 (0.011)	4.4 (0.13)
Random Forest	4.050 (0.062)	NA	NA	10.0 (0.00)
GBM	1.935 (0.039)	NA	NA	10.0 (0.00)
ORACLE	1.160 (0.034)	0.000 (0.000)	1.000 (0.000)	4.0 (0.00)

In Table 2 we can compare the risk and variable selection capability of the ACOSSO to the COSSO and the other methods on Example 1 with X uniform on [0, 1]¹⁰. Notice that all four of the ACOSSO methods are significantly better than COSSO and the other methods in terms of risk. COSSO, MARS, GAM, Random Forest and GBM have 131%, 180%, 150%, 349%, and 167% the risk of the ORACLE respectively, while the ACOSSO methods all have risk less than 108% that of the ORACLE. In terms of variable selection, the two ACOSSO-5CV methods again have a much higher average type I error rate than the two ACOSSO-BIC methods and MARS. In fact, ACOSSO-5CV-T has ᾱ = .25 which is quite high. Both ACOSSO-BIC methods however, have ᾱ ≤ 0.03 and have an average model size of close to 4.0, the correct number of components.

Although the ACOSSO-5CV methods have higher ᾱ, they have better power than the other methods as can be seen in the 1 − β̄ column of. Table 2. In this example, it turns out that 1 − β̄ is almost completely determined by how well the methods do at including the second variable (component P² f). The components P¹ f, P³ f, and P⁴ f were included in the model nearly 100% for all of the methods. The percentage of the realizations that included P² f was 65% for the ACOSSO-BIC methods, 75% for the COSSO and only 40% and 23% for MARS and GAM respectively. The percentage of the realizations that included P² f is close to 90% for the ACOSSO-5CV methods but as mentioned, the price paid is a higher type I error rate.

Example 2. This is a large p example with X ∈ ℜ⁶⁰. We observe n = 500 observations from y = f(X) + ε. The regression function is additive in the predictors,

$$f(\mathit{x})=g_1(x_1)+g_2(x_2)+g_3(x_3)+g_4(x_4)+1.5g_1(x_5)+1.5g_2(x_6)+1.5g_3(x_7)+1.5g_4(x_8)+2g_1(x_9)+2g_2(x_{10})+2g_3(x_{11})+2g_4(x_{12}),$$

where g₁,…, g₄ are given in (13). The noise variance is set to σ² = 2.40 yielding a SNR of 3:1 in the uniform case. Notice that X₁₃,…,X₆₀ are uninformative. In this example, we consider the same two distributional families for the input vector X as in Lin & Zhang (2006).

Compound Symmetry

For an input X = (X₁,…,X_p), let X_j = (W_j+tU)/(1+t), j = 1,…,p, where W₁,…,W_p and U are iid from Unif(0, 1). Thus, Corr(X_j, X_k) = t²/(1 + t²) for j ≠ k. The uniform distribution design corresponds to the case t = 0. (trimmed) AR(1): Let W₁,…,W_d be iid 𝒩 (0, 1), and let X₁ = W₁, X_j = ρX_j−1 + (1 − ρ²)^1/2W_j, j = 2,…,p. Then trim X_j in [−2.5, 2.5] and scale to [0, 1].

Table 3 shows the results of estimation risk (standard error in parentheses) on six different cases which correspond to different distributions for the predictors. Again the ACOSSO methods have estimation risk much closer to ORACLE than the other methods. COSSO and GAM have very similar performance in this example and generally have the best risk among the methods other than ACOSSO. One notable exception is the extremely high correlation case (Compound Symmetry, t = 3, where Corr(X_j, X_k) = .9 for j ≠ k). Here the ACOSSO-BIC-T and ACOSSO-5CV-T seem to struggle a bit as they have risk near or above the risk of COSSO and GAM. GBM actually has the best risk in this particular case. However, the ACOSSO variants are substantially better overall than any of the other methods. A similar trend was also noticed (table not presented) for these six different cases on the test function from Example 1.

Table 3.

Estimation Risk based on 100 realizations from Example 2 under various Covariance Structures; standard error given in parantheses.

	Compound Symmetry			Trimmed AR(1)
	t = 0	t = 1	t = 3	ρ = −0.5	ρ = 0.0	ρ = 0.5
ACOSSO-5CV-T	0.41 (0.01)	0.41 (0.01)	0.52 (0.01)	0.40 (0.01)	0.40 (0.01)	0.40 (0.01)
ACOSSO-5CV-C	0.42 (0.01)	0.40 (0.01)	0.43 (0.01)	0.40 (0.01)	0.40 (0.01)	0.40 (0.01)
ACOSSO-BIC-T	0.42 (0.01)	0.41 (0.01)	0.60 (0.02)	0.42 (0.01)	0.39 (0.01)	0.42 (0.01)
ACOSSO-BIC-C	0.42 (0.01)	0.42 (0.01)	0.47 (0.01)	0.45 (0.02)	0.39 (0.01)	0.43 (0.01)
COSSO	0.48 (0.01)	0.60 (0.01)	0.54 (0.01)	0.60 (0.02)	0.57 (0.01)	0.57 (0.01)
MARS	0.97 (0.02)	0.66 (0.01)	1.05 (0.02)	0.64 (0.01)	0.62 (0.01)	0.64 (0.01)
GAM	0.49 (0.01)	0.52 (0.01)	0.50 (0.01)	0.52 (0.01)	0.52 (0.01)	0.52 (0.01)
Random Forest	1.86 (0.01)	1.50 (0.01)	0.76 (0.00)	1.26 (0.01)	1.19 (0.01)	1.25 (0.01)
GBM	0.73 (0.01)	0.52 (0.01)	0.47 (0.00)	0.58 (0.01)	0.58 (0.01)	0.57 (0.01)
ORACLE	0.30 (0.00)	0.28 (0.00)	0.27 (0.00)	0.29 (0.00)	0.29 (0.01)	0.29 (0.01)

Example 3. Here we consider a regression model with 10 predictors and several two way interactions. The regression function is

$$f(\mathit{x})=g_1(x_1)+g_2(x_2)+g_3(x_3)+g_4(x_4)+g_3(x_1{x}_2)+g_2((x_1+x_3)/2)+g_1(x_3{x}_4)$$

so that x₅,…, x₁₀ are uninformative. The noise variance is set at σ² = 0.44098 to give a SNR of 3:1. Here, we consider only the uniform distribution on the predictors and evaluate performance at various sample sizes, n = 100, n = 250, and n = 500.

A summary of the estimation risk on 100 realizations can be found in Table 4. When n = 100 we see that COSSO seems to struggle a bit as all of the other methods except Random Forest have substantially better risk. However, the ACOSSO methods have risk comparable or better than the other methods and less than half that of COSSO. The estimation risk for all methods improves as the sample size increases. However, stepwise GAM does not improve from n = 250 to n = 500 probably because of its inability to model the interactions in this example. Also notice that the ACOSSO methods maintain close to 50% the risk of COSSO for all sample sizes. In fact, for n = 500 the ACOSSO methods have risk nearly the same as that of the ORACLE and roughly half that of the next best methods (COSSO and GBM).

Table 4.

Estimation Risk based on 100 realizations from Example 3 with n = 100, 250, and 500; standard error given in parantheses.

	n = 100	n = 250	n = 500
ACOSSO-5CV-T	0.139 (0.017)	0.055 (0.001)	0.034 (0.001)
ACOSSO-5CV-C	0.120 (0.011)	0.055 (0.001)	0.036 (0.001)
ACOSSO-BIC-T	0.200 (0.027)	0.054 (0.001)	0.034 (0.001)
ACOSSO-BIC-C	0.138 (0.016)	0.050 (0.001)	0.034 (0.001)
COSSO	0.290 (0.016)	0.093 (0.002)	0.057 (0.001)
MARS	0.245 (0.021)	0.149 (0.009)	0.110 (0.008)
GAM	0.149 (0.005)	0.137 (0.001)	0.136 (0.001)
Random Forest	0.297 (0.006)	0.190 (0.002)	0.148 (0.001)
GBM	0.126 (0.003)	0.084 (0.001)	0.065 (0.001)
ORACLE	0.071 (0.003)	0.042 (0.001)	0.029 (0.000)

Computation Time

Table 5 gives the computation times (in seconds) for the various methods on the three sample size cases in Example 3. Recall that in Example 3 the number of predictors is p = 10, but the total number of functional components including interactions is q = 55. The times given are the average over the 100 realizations and include the time required for tuning parameter selection.

Table 5.

Average CPU time (in seconds) for each method to compute a model fit (including tuning parameter selection) for the various sample size simulations of Example 3.

	n = 100	n = 250	n = 500
ACOSSO-5CV-T	8.7	47.2	155.2
ACOSSO-5CV-C	10.5	49.7	163.6
ACOSSO-BIC-T	3.0	11.9	89.0
ACOSSO-BIC-C	3.9	26.6	118.4
COSSO	7.5	43.4	150.1
MARS	9.2	11.2	13.6
GAM	5.7	7.9	11.3
Random Forest	0.3	6.4	15.3
GBM	4.2	9.1	17.0

For larger sample sizes, ACOSSO and COSSO take significantly longer than the other methods. Considering the performance in the simulation examples and the computation times, the best overall ACOSSO variant seems to be ACOSSO-BIC-T. It is important to point out that the other methods (besides ACOSSO or COSSO) are computed via more polished R-packages that take advantage of the speed of compiled languages such as C or Fortran. The computing time of ACOSSO (and COSSO) could also be decreased substantially by introducing more efficient approximations and by taking advantage of a compiled language.

7 Application to Real Data

In this section we apply the ACOSSO to three real datasets. We only report the results of the two ACOSSO-BIC methods since they performed much better overall than the ACOSSO-5CV methods in our simulations. The first two data sets are the popular Ozone data and the Tecator data which were also used by Lin & Zhang (2006). Both data sets are available from the datasets archive of StatLib at http://lib.stat.cmu.edu/datasets/. The Ozone data was also used in Breiman & Friedman (1995), Buja, Hastie & Tibshirani (1989), and Breiman (1995). This data set contains the daily maximum one-hour-average ozone reading and 8 meteorological variables recorded in the Los Angeles basin for 330 days of 1976.

The Tecator data was recorded on a Tecator Infratec Food and Feed Analyzer. Each sample contains finely chopped pure meat with different moisture, fat and protein contents. The input vector consists of a 100 channel spectrum of absorbances. The absorbance is – log₁₀ of the transmittance measured by the spectrometer. As in Lin & Zhang (2006), we use the first 13 principal components to predict fat content. The total sample size is 215.

The third data set comes from a computer model for two phase fluid flow (Vaughn, Bean, Helton, Lord, MacKinnon & Schreiber 2000). Uncertainty/sensitivity analysis of this model was carried out as part of the 1996 compliance certification application for the Waste Isolation Pilot Plant (WIPP) (Helton & Marietta, editors 2000). There were 31 uncertain variables that were inputs into the two-phase fluid flow analysis; see Storlie & Helton (2008) for a full description. Here we consider only a specific scenario which was part of the overall analysis. The variable BRN-REPTC10K is used as the response. This variable corresponds to cumulative brine flow in m³ into the waste repository at 10,000 years assuming there was a drilling intrusion at 1000 years. The sample size is n = 300. This data set is available at http://www.stat.unm.edu/~storlie/acosso/.

We apply each of the methods on these three data sets and estimate the prediction risk, E[Y − f(X)]², by ten-fold cross validation. We select the tuning parameter using only data within the training set (i.e., a new value of the tuning parameter is selected for each of the 10 training sets without using any data from the test sets). The estimate obtained is then evaluated on the test set. We repeat this ten-fold cross validation 50 times and average. The resulting prediction risk estimates along with standard errors are displayed in Table 6. The interaction model is presented for all of the methods (except GAM) since it had better prediction accuracy on all three data sets than the additive model.

Table 6.

Estimated Prediction Risk for Real Data Examples; standard error given in parantheses. Risk for BRNREPTC10K for the WIPP data is in units of 100m⁶

	Ozone	Tecator	WIPP
ACOSSO-BIC-T	15.07 (0.07)	1.44 (0.02)	1.04 (0.00)
ACOSSO-BIC-C	14.81 (0.08)	1.38 (0.02)	1.05 (0.01)
COSSO	15.99 (0.06)	0.88 (0.02)	1.30 (0.01)
MARS	14.24 (0.12)	3.01 (0.17)	1.12 (0.01)
GAM	15.91 (0.12)	592.52 (4.26)	1.83 (0.01)
Random Forest	18.11 (0.07)	14.35 (0.10)	1.29 (0.01)
GBM	10.69 (0.00)	3.35 (0.00)	0.97 (0.00)

For the Ozone data set, the ACOSSO is comparable to MARS but better than COSSO, GAM and Random Forest. GBM seems to be the best method for prediction accuracy on this data set though. For the Tecator data, both the COSSO and ACOSSO are much better than all of the other methods. There are several significant interactions which is why GAM performs so poorly relative to the other methods here. Interestly, COSSO is better than ACOSSO here which shows that the adaptive weights aren’t always an advantage. The reason that COSSO performs better in this case is likely due to the fact that 12 out of the 13 variables are selected for inclusion into the model and around 62 out of the 91 total functional components are estimated to be non-zero, so this is not a very sparse model. Hence using all weights equal to 1 (the COSSO) should work quite well here. In cases like this, it may be that using adaptive weights in the ACOSSO can detract from the COSSO fit by adding more noise to the estimation process. In contrast, the WIPP data set has only about 8 informative input variables of the 31 inputs. Hence the ACOSSO significantly outperforms the COSSO and is comparable to GBM for prediction accuracy.

8 Conclusions & Further Work

In this article, we have developed the ACOSSO, a new regularization method for simultaneous model fitting and variable selection in the context of nonparametric regression. The relationship between the ACOSSO and the COSSO is analogous to that between the adaptive LASSO and the LASSO. We have explored a special case under which the ACOSSO has a nonparametric version of the oracle property, which the COSSO does not appear to possess. This is the first result of this type for a nonparametric regression estimator. In addition we have demonstrated that the ACOSSOoutperforms COSSO, MARS, and stepwise GAMs for variable selection and prediction on all simulated examples and all but one of the real data examples. The ACOSSO also has very competitive performance for prediction when compared with other well known prediction methods Random Forest and GBM. R code to fit ACOSSO models is available at http://www.stat.unm.edu/~storlie/acosso/.

It remains to show that ACOSSO has the np-oracle property under more general conditions such as random designs. It may also be possible to yet improve the performance of the ACOSSO by using a different weighting scheme. The Tecator example in Section 7, suggests that using a weight power, γ = 2 is not always ideal. Perhaps it would be better to cross validate on a few different choices of γ so that it could be chosen smaller in cases (such as the Tecator example) where the weights are not as helpful. In addition, there are certainly a number of other ways to use the initial estimate, f̃, in the creation of the penalty term. These are topics for further research.

captionPlot of ∥P^j f̂∥_L2 along with ∥P^j f∥_L2 by M for both ACOSSO and COSSO on a realization from Example 1.

Appendix

A Proofs

A.1 Equivalent Form

Proof of Lemma 1

Denote the functional in (6) by A(f) and the functional in (9) by B(θ, f). Since $a+b\ge 2\sqrt{\mathit{\text{ab}}}\text{for}a,b\ge 0,$, with equality if and only if a = b, we have for each j = 1,…, q

$${\mathrm{\lambda }}_0{\theta }_j^{-1}{w}_j^{2-\vartheta }{\parallel P^{j}f\parallel }_{ℱ}^2+{\mathrm{\lambda }}_1{w}_j^{\vartheta }{\theta }_j\ge 2{\mathrm{\lambda }}_0^{1/2}{\mathrm{\lambda }}_1^{1/2}{w}_j{\parallel P^{j}f\parallel }_{ℱ}=\mathrm{\lambda }{w}_j{\parallel P^{j}f\parallel }_{ℱ},$$

for any θ_j ≥ 0 and any f ∈ ℱ. Hence B(θ, f) ≥ A(f) with equality only when ${\theta }_j={\mathrm{\lambda }}_0^{1/2}{\mathrm{\lambda }}_1^{-1/2}{w}_j^{1-\vartheta }{\parallel P^j\widehat{f}\parallel }_{ℱ}$ and the result follows.

A.2 Convergence Rate

The proof of Theorem 1 uses Lemma 2 below which is a generalization of Theorem 10.2 of van de Geer (2000). Consider the regression model y_i = g₀(x_i)+ε_i, i = 1,…, n where g₀ is known to lie in a class of functions 𝒢, x_i’s are given covariates in [0, 1]^p, and ε_i’s are independent and sub-Gaussian as in (8). Let I_n : 𝒢 → [0,∞) be a pseudonorm on 𝒢. Define ${\widehat{g}}_n={\text{arg min}}_{g\in 𝒢}1/n{\displaystyle {\sum }_{i=1}^n{(y_i-g({\mathit{x}}_i))}^2+{\tau }_n^2{I}_n(g)}$. Let H_∞ (δ, 𝒢) be the δ-entropy of the function class 𝒢 under the supremum norm ∥g∥_∞ = sup_x |g(x)| (see van de Geer 2000 page 17).

Lemma 2

Suppose there exists I_* such that I_*(g) ≤ I_n(g) for all g ∈ 𝒢, n ≥ 1. Also assume that there exists constants A > 0 and 0 < α < 2 such that

$$H_{\infty }(\delta ,\{\frac{g-g_0}{I_{*}(g)+I_{*}(g_0)}:g\in 𝒢,I_{*}(g)+I_{*}(g_0)>0\left\}\right)\le A{\delta }^{-\alpha }$$ (A1)

for all δ > 0 and n ≥ 1. Then if I_*(g₀) > 0 and ${\tau }_n^{-1}=O_p(n^{1/(2+\alpha )})I_n^{(2-\alpha )/(4+2\alpha )}(g_0)$, we have $\parallel {\widehat{g}}_n-g_0\parallel =O_p({\tau }_n)I_n^{1/2}(g_0)$. Moreover, if I_n(g₀) = 0 for all n ≥ 1 then $\parallel {\widehat{g}}_n-g_0\parallel =O_p(n^{-1/(2-\alpha )}){\tau }_n^{-2\alpha /(2-\alpha )}$.

Proof. This follows the same logic as the proof of Theorem 10.2 of van de Geer (2000), so we have intentionally made the following argument somewhat terse. Notice that

$${\parallel {\widehat{g}}_n-g_0\parallel }_n^2+{\tau }_n^2{I}_n({\widehat{g}}_n)\le 2{(\epsilon ,{\widehat{g}}_n-g_0)}_n+{\tau }_n^2{I}_n(g_0).$$ (A2)

Also, condition (A1) along with Lemma 8.4 in van de Geer (2000) guarantees that

$$\underset{g\in 𝒢}{\text{sup}}\frac{|{(\epsilon ,{\widehat{g}}_n-g_0)}_n|}{{\parallel {\widehat{g}}_n-g_0\parallel }_n^{1-\alpha /2}{(I_{*}(g)+I_{*}(g_0))}^{\alpha /2}}=O_p(n^{-1/2}).$$ (A3)

Case (i) Suppose that I_*(ĝ_n) > I_*(g₀). Then by (A2) and (A3) we have

$$\begin{array}{cc}{\parallel {\widehat{g}}_n-g_0\parallel }_n^2+{\tau }_n^2{I}_n({\widehat{g}}_n)\hfill & \le O_p(n^{-1/2}){\parallel {\widehat{g}}_n-g_0\parallel }_n^{1-\alpha /2}{I}_{*}^{\alpha /2}({\widehat{g}}_n)+{\tau }_n^2{I}_n(g_0)\hfill \\ \hfill & \le O_p(n^{-1/2}){\parallel {\widehat{g}}_n-g_0\parallel }_n^{1-\alpha /2}{I}_n^{\alpha /2}({\widehat{g}}_n)+{\tau }_n^2{I}_n(g_0).\hfill \end{array}$$

The rest of the argument is identical to that on page 170 of van de Geer (2000). Case (ii) Suppose that I_*(ĝ_n) ≤ I_*(g₀) and I_*(g₀) > 0. By (A2) and (A3) we have

$$\begin{array}{cc}{\parallel {\widehat{g}}_n-g_0\parallel }_n^2\hfill & \le O_p(n^{-1/2}){\parallel {\widehat{g}}_n-g_0\parallel }_n^{1-\alpha /2}{I}_{*}^{\alpha /2}(g_0)+{\tau }_n^2{I}_n(g_0)\hfill \\ \hfill & \le O_p(n^{-1/2}){\parallel {\widehat{g}}_n-g_0\parallel }_n^{1-\alpha /2}{I}_n^{\alpha /2}(g_0)+{\tau }_n^2{I}_n(g_0).\hfill \end{array}$$

The remainder of this case is identical to that on page 170 of van de Geer (2000).

Proof of Theorem 1. The conditions of Lemma 2 do not hold directly for the ℱ and $I_n(f)={\displaystyle {\sum }_{j=1}^p{w}_{j,n}{\parallel P^{j}f\parallel }_{ℱ}}$ of Theorem 1. The following orthogonality argument used in van de Geer (2000) and Lin & Zhang (2006) works to remedy this problem though. For any f ∈ ℱ we can write f(x) = b + g(x) = b + f₁(x₁) +⋯+ f_p(x_p), such that ${\displaystyle {\sum }_{i=1}^n{f}_j(x_{j,i})=0,j=1,\dots ,p}$. Similarly write f̂(x) =b̂ + ĝ(x) and f₀(x) = b₀+g₀(x). Then ${\displaystyle {\sum }_{i=1}^n(g(x_i)-g_0({\mathit{x}}_i))}=0$, and we can write (6) as

$${(b_0-b)}^2+\frac{2}{n}(b_0-b){\displaystyle \sum _{i=1}^n{\epsilon }_i+\frac{1}{n}{\displaystyle \sum _{i=1}^n{(g_0({\mathit{x}}_i)-g({\mathit{x}}_i))}^2+{\mathrm{\lambda }}_n{\displaystyle \sum _{j=1}^p{w}_{j,n}{\parallel P^{j}g\parallel }_{ℱ}.}}}$$

Therefore b̂ must minimize ${(b_0-b)}^2+2/n(b_0-b){\displaystyle {\sum }_{i=1}^n{\epsilon }_i}$ so that $\widehat{b}=b_0+1/n{\displaystyle {\sum }_i{\epsilon }_i}$. Hence (b̂ − b₀)² = O_p(n⁻¹). On the other hand, ĝ must minimize

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{(g_0({\mathit{x}}_i)-g({\mathit{x}}_i))}^2+{\mathrm{\lambda }}_n{\displaystyle \sum _{j=1}^p{w}_{j,n}{\parallel P^{j}g\parallel }_{ℱ}}}$$ (A4)

over all g ∈ 𝒢 where

$$𝒢=\{g\in ℱ:g(\mathit{x})=f_1(x_1)+\cdots +f_p(x_p),{\displaystyle \sum _{i=1}^n{f}_j(x_{j,i})=0,j=1,\dots ,p\}.}$$ (A5)

Now rewrite (A4) as

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{(g_0({\mathit{x}}_i)-g({\mathit{x}}_i))}^2+{\tilde{\lambda }}_n}{\displaystyle \sum _{j=1}^p{\tilde{w}}_{j,n}{\parallel P^{j}g\parallel }_{ℱ},}$$ (A6)

where λ̃_n = λ_nw_*,n, w_*,n = min {w_1,n,…,w_p,n}, and w̃_j,n = w_j,n/w_*,n.

The problem is now reduced to showing that the conditions of Lemma 2 hold for ${\tau }_n^2={\tilde{\lambda }}_n\text{and}{\text{I}}_n(g)={\displaystyle {\sum }_{j=1}^p{\tilde{w}}_{j,n}{\parallel P^{j}g\parallel }_{ℱ}}$. However, notice that min {w̃_1,n,…, w̃_p,n} = 1 for all n. This implies that $I_n(g)\ge I_{*}(g)={\displaystyle {\sum }_{j=1}^p{\parallel P^{j}g\parallel }_{ℱ}}$ for all g ∈ 𝒢 and n ≥ 1. Also notice that the entropy bound in (A1) holds whenever

$$H_{\infty }(\delta ,\{g\in 𝒢:I_{*}(g)\le 1\})\le A{\delta }^{-\alpha },$$ (A7)

since I_*(g − g₀) ≤ I_*(g) + I_*(g₀) so that the set in brackets in (A7) contains that in (A1). And (A7) holds by Lemma 4 in the COSSO paper with α = 1/2. We complete the proof by treating the cases U^c not empty and U^c empty separately.

Case (i) Suppose that P^j f ≠ 0 for some j. Then I_*(g₀) > 0. Also, $w_{*,n}^{-1}=O_p(1)$ and w_j,n = O_p (1) for j ∈ U^c by assumption. This implies that w̃_j,n = O_p(1), for j ∈ U^c so that I_n(g₀) = O_p(1). Also ${\tilde{\lambda }}_n^{-1}=O_p(1){\mathrm{\lambda }}_n^{-1}=O_p(n^{4/5})$. The result now follows from Lemma 2.

Case (ii) Suppose now that P^j f = 0 for all j. Then I_n (g₀) = 0 for all n and the result follows from Lemma 2.

Proof of Corollary 1. For the traditional smoothing spline with λ₀ ~ n^−4/5 it is known (Lin 2000) that ∥P^j f̃ − P^j f₀∥_L2 = O_p(n^−2/5). This implies |∥P^j f̃∥_L2 − ∥P^j f₀∥_L2 | ≤ O_p(n^−2/5). Hence $w_{j,n}^{-1}=O_p(1)$ for j = 1,…, p and w_j,n = O_p(1) for j ∈ U^c, which also implies w_*,n = O_p(1). The conditions of Theorem 1 are now satisfied and we have ∥f − f_n∥ = O_p(n^−2/5) if P^jf ≠ 0 for some j. On the other hand, also notice that $w_{j,n}^{-1}=O_p(n^{-2\gamma /5})$ for j ∈ U. Hence $w_{*,n}^{-1}=O_p(n^{-2\gamma /5})$ whenever P^j f = 0 for all j so that $n^{-2/3}{\lambda }_n^{-1/3}{w}_{*,n}^{-1/3}=O_p(n^{-1/2})$ for γ > 3/4 and the result follows.

A.3 Oracle Property

Proof of Theorem 2. Define $\mathbf{\Sigma }={\{\overline{K}(x_{1,i},x_{1,j})\}}_{i,j=1}^m$, the m × m marginal Gram matrix corresponding to the reproducing kernel for ${\overline{𝒮}}_{\text{per}}^2$. Also let K_j stand for the n × n Gram matrix corresponding to the reproducing kernel for the reproducing kernel for ${\overline{𝒮}}_{\text{per}}^2$ on variable x_j, j = 1,…, p. Let 1_m be a vector of m ones. Assuming the observations are permuted appropriately, we can write

$$\begin{array}{cc}{\mathit{K}}_1\hfill & =\mathbf{\Sigma }\otimes ({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\otimes \cdots \otimes ({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\hfill \\ {\mathit{K}}_2\hfill & =({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\otimes \mathbf{\Sigma }\otimes \cdots \otimes ({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\hfill \\ \hfill & ⋮\hfill \\ {\mathit{K}}_p\hfill & ({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\otimes \cdots \otimes ({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })\otimes \mathbf{\Sigma },\hfill \end{array}$$

where ⊗ here stands for the Kronecker product between two matrices.

Straightforward calculation shows that Σ1_m = 1/(720m³)1_m. So write the eigen-vectors of Σ as {υ₁ = 1_m, υ₂,…, υ_m} and let ϒ be the m × m matrix with these eigenvectors as its columns. The corresponding eigenvalues are {mϕ₁, mϕ₂,…,mϕ_m}, where ϕ₁ = 1/(720m⁴) and ϕ₂ ≥ ϕ₃ ≥ ⋯ ≥ ϕ_m. It is known (Uteras 1983) that ϕ_i ~ i⁻⁴ for i ≥ 2. Notice {υ₁, υ₂,…, υ_m} are also the eigenvectors of $({\mathbf{1}}_m{\mathbf{1}}_m^{\prime })$ with eigenvalues {m, 0,…, 0}. Write O = ϒ ⊗ ϒ ⊗ ⋯ ⊗ ϒ and let ξ_i be the i^th column of O, i = 1,…, n. It is easy to verify that {ξ₁,…, ξ_n} form an eigensystem for each of K₁,…,K_p.

Let {ζ_1,j,…, ζ_n,j} be the collection of vectors {ξ₁,…, ξ_n} sorted so that those corresponding to nonzero eigenvalues for K_j are listed first. Specifically, let

$$\begin{array}{cc}{\mathit{\varsigma }}_{i,1}\hfill & ={\mathit{\upsilon }}_i\otimes {\mathbf{1}}_m\otimes \cdots \otimes {\mathbf{1}}_m,\hfill \\ {\mathit{\varsigma }}_{i,2}\hfill & ={\mathbf{1}}_m\otimes {\mathit{\upsilon }}_i\otimes \cdots \otimes {\mathbf{1}}_m,\hfill \\ \hfill & ⋮\hfill \\ {\mathit{\varsigma }}_{i,p}\hfill & ={\mathbf{1}}_m\otimes {\mathbf{1}}_m\otimes \cdots \otimes {\mathit{\upsilon }}_i,\hfill \end{array}$$ (A8)

for i = 1,…,m. Notice that each ζ_i,j, i = 1,…,m, j = 1,…, p corresponds to a distinct ξ_k, for some k ∈ {1,…, n}. So let the first m elements of the collection {ζ_1,j,…, ζ_m,j, ζ_m+1,j,…, ζ_n,j} be given by (A8) and the remaining n − m be given by the remaining ξ_i in any order. The corresponding eigenvalues are then

$${\eta }_{i,j}=\{\begin{array}{cc}n{\varphi }_i\hfill & \text{for}i=1,\dots ,m\hfill \\ 0\hfill & \text{for}i=m+1,\dots ,n\hfill \end{array}.$$

It is clear that {ξ₁,…, ξ_n} is also an orthonormal basis in ℜⁿ with respect to the inner product

$${\langle \mathit{u},\mathit{\upsilon }\rangle }_n=1/n{\displaystyle \sum _i{u}_i{\upsilon }_i.}$$ (A9)

Let f = (f(x₁),…, f(x_n))′. Denote a = (1/n)O′ f and z = (1/n)O′y. That is, z_i = 〈y, ξ_i〉_n, a_i = 〈f, ξ_i〉_n, δ_i = 〈ε, ξ_i〉_n and we have that z_i = a_i + δ_i. With some abuse of notation, also let

$$z_{i,j}={\langle \mathit{y},{\mathit{\varsigma }}_{i,j}\rangle }_n,a_{i,j}={\langle \mathit{f},{\mathit{\varsigma }}_{i,j}\rangle }_n,{\delta }_{i,j}={\langle \mathit{\epsilon },{\mathit{\varsigma }}_{i,j}\rangle }_n.$$

Now, using ϑ = 2 in (9), the ACOSSO estimate is the minimizer of

$$\frac{1}{n}(\mathit{y}-{\mathit{K}}_{\theta }\mathit{c}-b{\mathbf{1}}_n)\prime (\mathit{y}-{\mathit{K}}_{\theta }\mathit{c}-b{\mathbf{1}}_n)+\mathbf{c}\prime {\mathit{K}}_{\theta }\mathit{c}+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^p{w}_j^2{\theta }_j,}$$ (A10)

where ${\mathit{K}}_{\theta }={\displaystyle {\sum }_{j=1}^p{\theta }_j{\mathit{K}}_j}$. Let s = O′c and D_j = (1/n²)O′K_jO is a diagonal matrix with diagonal elements ϕ_i. Then (A10) is equivalent to

$$(z-{\mathit{D}}_{\theta }\mathit{s}-(b,0,\dots 0)\prime )\prime (z-{\mathit{D}}_{\theta }\mathit{s}-(b,0,\dots 0)\prime )+\mathit{s}\prime {\mathit{D}}_{\theta }\mathit{s}+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^p{w}_j^2{\theta }_j,}$$ (A11)

where ${\mathit{D}}_{\theta }={\displaystyle {\sum }_{j=1}^p{\theta }_j{\mathit{D}}_j}$. Straightforward calculation shows that this minimization problem is equivalent to

$$\ell (\mathit{s},\mathit{\theta })={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^p{(z_{\mathit{\text{ij}}}-{\varphi }_i{\theta }_j{s}_{\mathit{\text{ij}}})}^2+}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^p{\varphi }_i{\theta }_j{s}_{\mathit{\text{ij}}}^2+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^p{w}_j^2{\theta }_j,}}}}$$ (A12)

where $s_{\mathit{\text{ij}}}={\mathit{\varsigma }}_{\mathit{\text{ij}}}^{\prime }\mathit{c},i=1,\dots ,m,$, j = 1,…,p are distinct elements of s.

Now, we first condition on θ and minimize over s. Given θ, ℓ(s, θ) is a convex function of s and is minimized at $\widehat{\mathit{s}}(\mathit{\theta })={{\{{\widehat{s}}_{\mathit{\text{ij}}}({\theta }_j)\}}_{i=1}^m}_{j=1}^p$, where ŝ_ij(θ_j) = z_ij(1 − ϕ_iθ_j). Inserting ŝ(θ) into (A12) gives

$$\begin{array}{cc}\ell (\widehat{\mathit{s}}(\mathit{\theta }),\mathit{\theta })\hfill & ={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^p\frac{z_{\mathit{\text{ij}}}^2}{{(1+{\varphi }_i{\theta }_j)}^2}+{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^p\frac{{\varphi }_i{\theta }_j{z}_{\mathit{\text{ij}}}^2}{{(1+{\varphi }_i{\theta }_j)}^2}+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^p{w}_j^2{\theta }_j}}}}}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^p\frac{z_{\mathit{\text{ij}}}^2}{1+{\varphi }_i{\theta }_j}+{\mathrm{\lambda }}_1{\displaystyle \sum _{j=1}^p{w}_j^2{\theta }_j.}}}\hfill \end{array}$$ (A13)

Notice that ℓ(ŝ(θ), θ) is continuous in θ_j,

$$\frac{{\partial }^2\ell (\widehat{\mathit{s}}(\mathit{\theta }),\mathit{\theta })}{\partial {\theta }_j^2}=2{\displaystyle \sum _{i=1}^m\frac{z_{\mathit{\text{ij}}}^2{\varphi }_i^2}{{(1+{\varphi }_i{\theta }_j)}^3}>0\text{for each}j}$$ (A14)

and ∂² ℓ(ŝ (θ), θ)/∂θ_j∂θ_k = 0 for j ≠ k. Therefore ℓ(s, θ) is convex and has a unique minimum, θ̂.

Clearly, P^j f̂ ≡ 0 if and only if θ̂_j = 0. So it suffices to consider θ̂_j. As such, since we must have that θ_j ≥ 0, the minimizer, θ̂_j = 0 if and only if

$$\frac{\partial }{\partial {\theta }_j}\ell (\widehat{\mathit{s}}(\mathit{\theta }),\mathit{\theta }){|}_{{\theta }_{j=0}}\ge 0,$$

which is equivalent to

$$T=n{\displaystyle \sum _{i=1}^m{\varphi }_i{z}_{\mathit{\text{ij}}}^2\le n{w}_{j,n}^2{\mathrm{\lambda }}_{1,n}.}$$ (A15)

If we assume that P^j f = 0, then we have z_ij = δ_ij. In the following, we will obtain bounds for E(T) and Var(T) to demonstrate that T is bounded in probability when P^j f = 0. To this end, we first obtain bounds for $\mathrm{E}({\delta }_{\mathit{\text{ij}}}^2)\text{and Var}({\delta }_{\mathit{\text{ij}}}^2)$. Recall that ${\delta }_{\mathit{\text{ij}}}=(1/n){\mathit{\varsigma }}_{\mathit{\text{ij}}}^{\prime }\mathit{\epsilon }$ and that the individual elements of ε are independent with E(ε) = 0. For notational convenience, let ξ = ζ_ij which is some column of the O matrix. Also, recall that the vector ξ is orthonormal with respect to the inner product in (A9). Now,

$$\begin{array}{cc}E({\delta }_{\mathit{\text{ij}}}^2)\hfill & =\frac{1}{n^2}E[{(\mathit{\xi }\prime \mathit{\epsilon })}^2]\hfill \\ \hfill & =\frac{1}{n^2}E({\displaystyle \sum _{a=1}^n{\displaystyle \sum _{b=1}^n{\xi }_a{\xi }_b{\epsilon }_a{\epsilon }_b)}}\hfill \\ \hfill & =\frac{1}{n^2}{\displaystyle \sum _{a=1}^n{\xi }_a^{2}E({\epsilon }_a^2)}\hfill \\ \hfill & \le \frac{1}{n^2}{\displaystyle \sum _{a=1}^n{\xi }_a^2{M}_1}\hfill \\ \hfill & =\frac{M_1}{n}\hfill \end{array}$$ (A16)

where $M_1={\text{max}}_a\mathrm{E}({\epsilon }_a^2)$ which is bounded because of the sub-Gaussian condition (8).

The variance of ${\delta }_{\mathit{\text{ij}}}^2$ is

$$\begin{array}{cc}\text{Var}({\delta }_{\mathit{\text{ij}}}^2)\hfill & =\text{Var}({\displaystyle \sum _{a=1}^n{\displaystyle \sum _{b=1}^n{\xi }_a{\xi }_b{\epsilon }_a{\epsilon }_b)}}\hfill \\ \hfill & ={\displaystyle \sum _{a=1}^n{\displaystyle \sum _{b=1}^n{\displaystyle \sum _{c=1}^n{\displaystyle \sum _{d=1}^n{\xi }_a{\xi }_b{\xi }_c{\xi }_d\text{Cov}({\epsilon }_a{\epsilon }_b,{\epsilon }_c{\epsilon }_d).}}}}\hfill \end{array}$$ (A17)

But ε_a’s are independent, so Cov(ε_aε_b, ε_cε_d) ≠ 0 only in the three mutually exclusive cases (i) a = b = c = d, (ii) a = c and b = d with a ≠ b, or (iii) a = d and b = c with a ≠ b. Thus, (A17) becomes,

$$\begin{array}{cc}\text{Var}({\delta }_{\mathit{\text{ij}}}^2)\hfill & =\frac{1}{n^4}[{\displaystyle \sum _{a=1}^n{\xi }_a^4\text{Cov}({\epsilon }_a^2,{\epsilon }_a^2)+2{\displaystyle \sum _{a=1}^n{\displaystyle \sum _{b\ne a}^n{\xi }_a^2{\xi }_b^2\text{Cov}({\epsilon }_a{\epsilon }_b,{\epsilon }_a{\epsilon }_b)]}}}\hfill \\ \hfill & \le \frac{2}{n^4}{\displaystyle \sum _{a=1}^n{\displaystyle \sum _{b=1}^n{\xi }_a^2{\xi }_b^2\text{Var}({\epsilon }_a{\epsilon }_b)}}\hfill \\ \hfill & \le \frac{2M_2}{n^4}{\left({\displaystyle \sum _{a=1}^n{\xi }_a^2}\right)}^2\hfill \\ \hfill & =\frac{2M_2}{n^2}\hfill \end{array}$$ (A18)

where M₂ = max_a,b{Var(ε_aε_b)} which is bounded because of the sub-Gaussian condition in (8). Notice that the derivations of the bounds in (A16) and (A18) do not depend on i or j (i.e., they do not depend on which column of O that ξ comes from). Thus, the bounds in (A16) and (A18) are uniform for all i.

Using (A16) we can write E(T) as

$$E(T)=n{\displaystyle \sum _{i=1}^m{\varphi }_{i}E[{\delta }_{\mathit{\text{ij}}}^2]\le M_1{\displaystyle \sum _{i=1}^m{\varphi }_i\sim M_1}.}$$ (A19)

Further, we can use (A18) to write Var(T) as

$$\begin{array}{cc}\text{Var}(T)=\hfill & n^2\text{Var}\left({\displaystyle \sum _{i=1}^m{\varphi }_i}{\delta }_{\mathit{\text{ij}}}\right)\hfill \\ \hfill & =n^2{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{l=1}^m{\varphi }_k{\varphi }_l\text{Cov}({\delta }_{k,j}^2,{\delta }_{l,j}^2)}}\hfill \\ \hfill & \le 2M_2{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{l=1}^m{\varphi }_k{\varphi }_l}}\hfill \\ \hfill & =2M_2{\left({\displaystyle \sum _{k=1}^m{\varphi }_k}\right)}^2\hfill \\ \hfill & \sim 2M_2.\hfill \end{array}$$ (A20)

Finally, as n increases, (A19) and (A20) guarantee that the left-hand side of (A15) is bounded in probability when P^j f = 0. Assuming that $n{w}_{j,n}^2{\lambda }_n^2\stackrel{p}{\to }\infty$ or equivalently that $n{w}_{j,n}^2{\lambda }_{1,n}\stackrel{p}{\to }\infty$ by Lemma 1, the right-hand side of (A15) increases to ∞ in probability. Therefore, if P^j f = 0 then θ̂_j = 0 with probability tending to one. If on the other hand $n{w}_{j,n}^2{\mathrm{\lambda }}_n^2=O_p(1)$, then the probability that $T>n{w}_{j,n}^2{\mathrm{\lambda }}_{1,n}$ converges to a positive constant. Hence the probability that θ̂_j > 0 converges to a positive constant.

Proof of Corollary 2. It is straightforward to to show that Theorem 1 still holds with ${𝒮}_{\text{per}}^2$ in place of 𝒮². Also recall from the proof of Corollary 1 that these weights satisfy the conditions of Theorem 1. Also, since $w_{j,n}^{-1}=O_p(n^{-2\mathrm{\gamma }/5})$ for j ∈ U we have $n{w}_{j,n}^2{\mathrm{\lambda }}_2^n\stackrel{p}{\to }\infty$ for j ∈ U whenever γ > 3/4. The conditions of Theorem 2 are now satisfied. Lastly, in light of Theorem 1, we also know that if P^j f ≠ 0, the probability that P^j f̂ ≠ 0 also tends to one as the sample size increases due to the consistency. Corollary 2 follows.