Freehand determination of the trajectory angle for cervical lateral mass screws: how accurate is it?

Abstract

Different methods of lateral mass screw placement in the cervical spine have been described with separate trajectories for each technique in the sagittal and parasagittal planes. In the latter, plane 30° has been recommended in the modified Magerl’s technique as the optimum angle to avoid injury to the vertebral artery and nerve root. The estimation of this angle remains arbitrary and very much operator dependant. The aim of this study was to assess how accurately the lateral trajectory angle of 30° is achieved by visual estimation amongst experienced surgeons in a tertiary spinal unit and to determine the likelihood of neurovascular injury during the procedure. We chose an anatomical ‘sawbone’ model of the cervical spine with simulated lordosis. The senior author marked the entry points. Five spinal consultants and five senior spinal fellows were asked to insert 1.6-mm K wires into the lateral masses of C3 to C6 bilaterally at 30° to the midsagittal plane using the marked entry points. The lateral angulation in the transverse plane was measured using a custom protractor and documented for each surgeon at each level and side. The mean and standard deviation (SD) of the data were obtained to determine the inter observer variability. Utilising this data, measurements were then made on a normal axial computerised tomography (CT) scan of the cervical spine of an anonymous patient to determine if there would have been any neurovascular compromise. Among the 10 surgeons, a total of 80 insertion angles were measured from C3 to C6 on either side. The overall mean angle of insertion was 25.15 (range 20.4–34.8). The overall SD was 4.78. Amongst the 80 measurements between the ten surgeons, two episodes of theoretical vertebral artery violation were observed when the angles were simulated on the CT scan. A moderate but notable variability in trajectory placement exists between surgeons during insertion of cervical lateral mass screws. Freehand estimation of 30° is not consistently achieved between surgeons and levels. In patients with gross degenerative or deformed cervical spine anatomy, this may increase the risk of neurovascular injury. The use of the ipsilateral lamina as an anatomical reference plane is supported.

Introduction

Several techniques of cervical lateral mass screw fixation have been described following the initial description by Roy-Camille [1, 2]. Each has been further modified to improve bone purchase and reduce the risk of injury to the adjacent neurovascular structures. The Magerl [3], Roy-Camille [1], An [4] and Anderson [5]) techniques are the most widely used. Each technique describes a separate starting point on the lateral mass as well as an optimum cranio-caudal and lateral angle for safe screw placement (Table 1). Although lateral mass screws are considered as safe, injuries to the spinal cord, nerve root, vertebral artery and facet joint have been reported [4, 6–8]. The optimum trajectory to avoid injuring the vertebral artery and nerve root has been described to be 30° lateral and 15° cephalad from anatomical studies [4]. With most techniques, the cranio-caudal angle is parallel to the superior articular facet which may be used as an anatomical guide of the trajectory. The lateral trajectory, however, is completely dependent on the visual estimation of the surgeon. Medial deviation of this trajectory (less than 20°) can result in neurovascular injury. This study aims to determine how accurately ten experienced spinal surgeons could determine the 30° axial trajectory angle for placement of cervical lateral mass instrumentation and if there would have been any violation of the transverse foramen during the procedure.

Table 1.

Common techniques for lateral mass screw insertion [1, 3–5, 10]

Techniques	Starting point	Lateral angle (°)	Cranio-caudal angle
Magerl	2 mm medial and superior to the centre of the lateral mass (LM)	25	Oriented parallel to the surface of the superior articular process
Modified Magerl	2 mm inferior to the inferior most edge of the superior facet and 2 mm medial to the posterior midline of the LM	30	Parallel to the surface of the superior articular process
Roy-Camille	Centre of the LM	10	Perpendicular to the posterior cortex of the vertebral body
Ann	1 mm medial to centre of LM	30	15 degrees cephalad
Anderson	1 mm medial to the centre of the LM	10	Parallel to facet joint

Materials and methods

Five senior fellows who had completed their training in Neurosurgery or Orthopaedic Surgery and were in full time spinal training and five full time spinal consultants dedicated only to spine surgery in a tertiary spinal unit of an university hospital participated in this study.

A saw bone model of the cervical spine with simulated lordosis fixed in place in a mould (Fig. 1) to guarantee a perfect horizontal plane was chosen. For consistency, an entry point was made at each level by the senior author 2 mm superior and medial to the midpoint of the LM. Each surgeon was asked to insert 2.5-mm Kirshner (k) wires into the lateral masses (LM) of a cervical (C) spine model simulating screw placement from C3 to C6 levels on both sides using the modified Magerl’s technique of 30° lateral angulation. The actual angle obtained was measured in the transverse plane by two separate observers with the help of a customised protractor (Fig. 2). The surgeons were not informed of the angles derived. The focus was placed on the axial or lateral angle and the cranio-caudal angle was not measured as this was aligned with the joint above. The data were collected for all the levels from C3 to C6 bilaterally for all ten surgeons. A total of 80 angles were derived from the group as a whole and tabulated in a Microsoft Excel spreadsheet (Table 2). The error or deviation from 30° was determined for each surgeon and for the group of fellows and consultants. Standard statistical analyses such as mean, standard deviation (SD) and coefficient of variation (CV) were calculated to assess the consistency of each surgeon as well as between the group of fellows and consultants. We used CV to determine the ‘relative variability’.

Fig. 1.

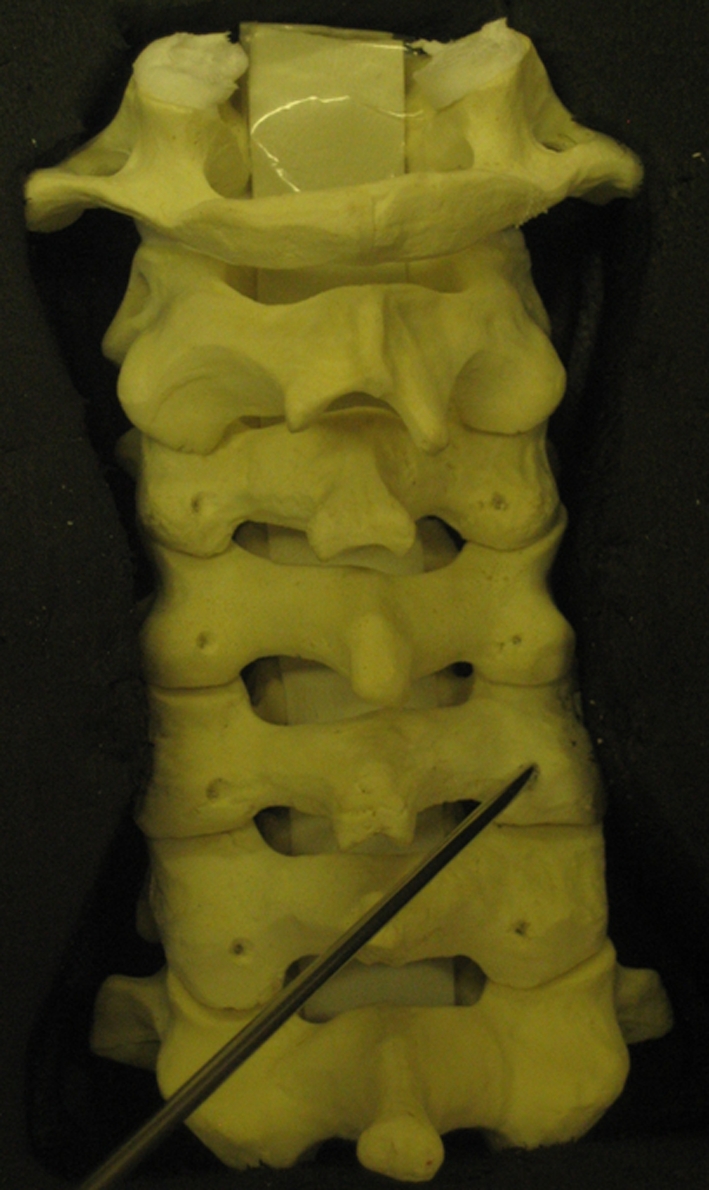
Saw bone model with lateral mass entry points

Fig. 2.

Custom protractor used to measure lateral mass insertion angle

Table 2.

Data collected from five fellows (F) and five consultants (C)

Level (side)	F1	F2	F3	F4	F5	C1	C2	C3	C4	C5	Range	Mean	SD
C3 (left)	22	25	24	25	21	27	27	23	16	35	16–35	24.5	4.90
C3 (right)	21	29	30	26	28	23	26	19	26	38	19–38	26.6	5.30
C4 (left)	20	29	25	24	22	26	28	20	15	31	15–31	24	4.85
C4 (right)	25	26	24	30	30	29	23	23	24	34	23–30	26.8	3.74
C5 (left)	22	30	25	30	21	18	25	26	18	33	18–33	24.8	5.14
C5 (right)	25	27	23	25	29	26	24	19	21	36	19–36	25.5	4.67
C6 (left)	19	24	20	20	20	19	29	22	20	35	19–35	22.8	5.27
C6 (right)	22	26	27	22	29	26	27	23	23	37	22–37	26.2	4.49
Mean	22	27	24.8	25.3	25.0	24.3	26.1	21.9	20.4	34.875	16–35	24.5	4.90
SD	2.14	2.14	2.92	3.49	4.34	3.92	2.03	2.42	3.89	2.23
Range	19–25	24–30	20–30	20–30	20–30	18–29	23–29	19–23	15–26	31–38
Overall mean	25.15
Overall SD	4.78
Coeff variation	9.72	7.92	11.78	13.84	17.37	16.16	7.77	11.05	19.09	6.40

The CV is a way to summarise the variation of results from the mean. It represents the ratio of the SD to the mean, and is a useful statistic for comparing the degree of variation from one data series to another, even if the means are drastically different from each other. It is in essence a standardization of the SD that allows comparison of variability estimates regardless of the magnitude of the mean. When the CV is small compared to mean, the data scatter compared to the mean is small and when it is large, the amount of variation is large.

Finally, using axial CT sections on the Impax PACS system (Agfa), a virtual screw trajectory was drawn in the axial plane with the angles derived, to determine if the transverse foramen would have been breached.

Results

The angles obtained from C3 to C6 for the group of ten surgeons ranged from 15 to 38°. Amongst these 80 angles, 14 (17%) measured 20° or less. When the virtual trajectories of all 80 angles were drawn in the axial plane on a normal CT section of an anonymous patient using the PACS system (Agfa), two instances of transverse foraminal breach were demonstrated at C3 and C4 with trajectory angles of 16 and 15°, respectively. The mean lateral angulation (LA) for the group was 25.15° (range 20.4–34.8°); that of the fellows being 24.4° (22–27°) and for consultants 26.2° (20.4–34.8°). Mean deviation from 30° for the fellows was 5.2° and that of the consultants 6.4°. This difference was not statistically significant. The mean SD was 4.7 for all surgeons (5.8 for consultants and 3.3 for fellows). The CV ranged from 6.4 to 19.09 for consultants and 7.92–17.37 for fellows (Table 2).

Discussion

Lateral mass screws in the cervical spine have been successfully used to allow for a rigid posterior fixation. Since Roy-Camille originally described the procedure in 1972, several modifications of the technique have been described. The common techniques used have been those described by An, Anderson, Magerl and Roy-Camille [1, 4, 5, 9]. Biomechanical studies have shown that the Magerl technique produces a stronger, more rigid construct than other techniques [10, 11]. Although the reported neurovascular complication rates from LM screw malplacement are low, it is possible that they are underreported in the literature and injury to the vertebral artery, nerve root, as well as the facet joint remain a concern [7, 12–14].

Despite a defined landmark for the starting point of the LM screws with the Magerl technique, the axial screw trajectory does not follow any precise anatomical plane. Merola et al. [10] conducted an anatomical study to determine the optimum screw angulation for posterior cervical LM screws using 2-mm k wires and varying the trajectory in the axial plane from 0 to 30° in 10° increments to reproduce modifications of Anderson, Roy-Camille and Magerl techniques. They demonstrated that the artery and nerve root were consistently compromised at 0 and 10° but were safe at 20° or above at all levels between C3 and C7. The authors noted that decreasing the amount of lateral angulation in the parasagittal plane for each of the techniques reduces the average distance from the neurovascular structures. This is also supported by the anatomical studies of An [4], Xu [8] and Ebraheim et al. [6]. These studies have shown that the optimum screw trajectory to avoid injuring the vertebral artery and nerve root is 30° lateral and 15° cephalad.

Intraoperatively, it can however be difficult to accurately estimate the lateral trajectory angle. This is at the best a visual estimate of the individual surgeon. The incidence of injury to the neurovascular structures correlates with the level of training as suggested by the findings of Seybold et al. [15]. Chin et al. [16] suggested the use of the caudal spinous process as an accurate local anatomical guide for LM screw trajectory, whereby the authors acknowledge that this guide may change in patients with deformities. In the absence of any fixed anatomical guidance, the lateral trajectory angle is therefore likely to have an interobserver variability which at its extreme may place the neurovascular structures at risk. It was the aim of this investigation to determine the accuracy and consistency with which a group of experienced spine surgeons is able to replicate the lateral angulation of 30° required for LM screw placement.

The mean lateral angulation for the fellows was 24.4° and that of the consultants was 26.2° with SD of 3.3 and 5.8, respectively. Amongst the 80 trajectories obtained, a precise 30° trajectory angle was achieved in only five instances (6%) with the mean deviation from 30° for the fellows being 5.2° and that of the consultants being 6.4°. The virtual projections of these 80 trajectory angles produced two theoretical episodes of vertebral artery injury at left C3 and C4 at 15 and 16° angles, respectively. As noted by the CV (Table 2), there was a small and insignificant variability amongst individual surgeons but not amongst the group of fellows and consultants as a whole. The CV for the fellows was 12.12 (range 7.92–17.39) and for consultants 12.09 (range 6.40–19.09).

The 30° lateral trajectory angle was not achieved consistently by the majority of our surgeons, which highlights the poor reliability of visual estimation of the angle even amongst experienced, full time spinal surgeons.

The measurement of the trajectory angles using the customised protractor is a possible limitation of our study. The use of a CT scanner would provide the most precise measurements. The demonstrated lack of consistency amongst the surgeons in visual estimation of the precise lateral trajectory angle would however most likely not be altered.

While we accept that a precise 30° lateral trajectory is not an absolute necessity in a normal cervical spine, in patients with degenerative and deformed cervical spine or with aberrant vertebral arteries, it is likely to be more relevant and may increase the risk of neurovascular injury. In such settings, the use of an aiming device to improve the accuracy of screw placement may be justified. A suitable anatomical reference plane may also increase the safety and reliability of this procedure. As recently suggested by Bayley et al. [3], the ipsilateral lamina can be used as such a reference plane for placement of subaxial LM screws to achieve a more consistent trajectory and consistently avoid vertebral artery injury. Our findings would support use of this technique.

Conclusion

An accurate visual estimation of the trajectory angle for lateral mass screws is difficult and not consistently achieved. Even amongst experienced spinal surgeons, a moderate but notable variability is observed which may lead to neurovascular compromise.