Competitive Binding to Cuprous Ions of Protein and BCA in the Bicinchoninic Acid Protein Assay

Abstract

Although Bicinchoninic acid (BCA) has been widely used to determine protein concentration, the mechanism of interaction between protein, copper ion and BCA in this assay is still not well known. Using the Micro BCA protein assay kit (Pierce Company), we measured the absorbance at 562 nm of BSA solutions with different concentrations of protein, and also varied the BCA concentration. When the concentration of protein was increased, the absorbance exhibited the known linear and nonlinear increase, and then reached an unexpected plateau followed by a gradual decrease. We introduced a model in which peptide chains competed with BCA for binding to cuprous ions. Formation of the well-known chromogenic complex of BCA-Cu¹⁺-BCA was competed with the binding of two peptide bonds (NTPB) to cuprous ion, and there is the possibility of the existence of two new complexes. A simple equilibrium equation was established to describe the correlations between the substances in solution at equilibrium, and an empirical exponential function was introduced to describe the reduction reaction. Theoretical predictions of absorbance from the model were in good agreement with the measurements, which not only validated the competitive binding model, but also predicted a new complex of BCA-Cu¹⁺-NTPB that might exist in the final solution. This work provides a new insight into understanding the chemical bases of the BCA protein assay and might extend the assay to higher protein concentration.

INTRODUCTION

Since the original work of Smith et al. (1985) [1], bicinchoninic acid (BCA) has been widely used to determine protein concentration because of its ease of use, high sensitivity and tolerance of interfering species [2, 3]. This assay is based on two chemical reactions. The first is the reduction of cupric ions (Cu²⁺) to cuprous ions (Cu¹⁺) by the peptide bonds, known as the biuret reaction, and by some specific residues in an alkaline environment [1]. The second step is the chelation of one Cu¹⁺ with two BCA molecules (Fig. 1a), forming an intense purple complex, which has a peak absorbance at 562nm. The protein concentration in a solution is determined by comparing this absorbance with a standard curve of absorbance from varying bovine serum albumin (BSA) [1]. For the Micro BCA^TM Assay Kit of Pierce (23235#), the standard curve appears nonlinear above the working range of 0.5 to 20 µg/mL protein. The reason for this nonlinearity has not been investigated. When we increased the concentration of BSA up to 6000 µg/mL, an unexpected absorbance maximum was observed. The molar concentrations of cupric ions, BCA molecules and peptide bonds were calculated from the given contents of the kit. It was found that the absorbance maximum appeared where the peptide bonds were about six times more concentrated than the cupric ions. It is reasonable to assume that the excess peptide bonds compete with the BCA for binding to cuprous ion, thereby reducing production of the chromogenic group. We describe a study of this competition by experiments and theoretical modeling.

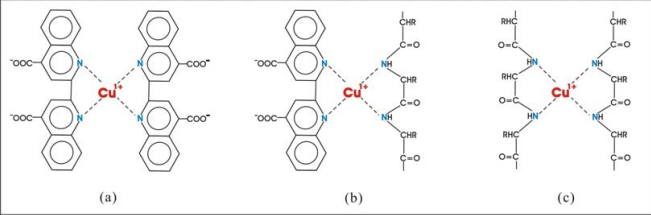
Fig. (1).

Three possible cuprous complexes can form during the BCA protein assay: a) BCA-Cu¹⁺-BCA; b) BCA-Cu¹⁺-NTPB; c) NTPBCu¹⁺-NTPB.

EXPERIMENTAL SECTION

Materials and Methods

Following the standard protocol for the Micro BCA Protein Assay Kit (23235#, Pierce Company), the working reagent (WR) was prepared from 25 parts of MA (sodium carbonate, sodium bicarbonate and sodium tartrate in 0.2 N NaOH), 24 parts of MB (4% BCA in water) and 1 part of MC (4% cupric sulfate, pentahydrate in water). A series of WR with increasing BCA was prepared with varying MB present in 24, 36.5, 49, 74, and 124 parts. The volumes of all WR solutions were kept constant by adding pure water so that only the BCA concentration varied. The pH value of all WR solutions was 11.16±0.06 measured with an Orion 310 pH meter. Twelve BSA solutions with concentrations ranging from 0.02 to 40 mg/mL were prepared by dissolving BSA powder (purity ≥ 99.9%, purchased from Bailingke Company, Beijing) in pure water. After mixing one part BSA solution with seven parts WR, a total of sixty solutions with varying concentrations of protein or BCA were obtained. The concentration given in the experimental results is that in the final mixture, and only the concentration of copper ions was invariant, 0.4 mM in all sample solutions. Each measurement was performed in duplicate.

The samples were incubated at 60 ˚C for one hour before cooling to room temperature in accordance with the standard procedures. All the absorbances were corrected by the corresponding blank replicate. The absorbance of the blank solution was 0.048±0.006. Absorbance at 562 nm was measured by spectrophotometer (Tianmei Company, Beijing) using glass cuvettes with optical path length of 0.1 cm.

Experimental Results

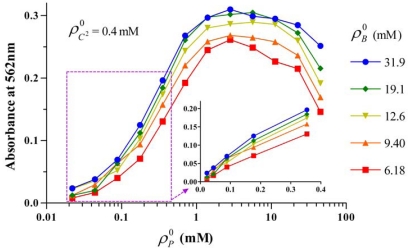
The measured absorbance data is shown in Fig. (2) where solutions with same BCA concentration are denoted by the same symbols. Each data point is the average of two replicates as well as corresponding standard errors. The figure shows that when the initial molar concentration of peptide bonds ${\mathit{\rho }}_P^0$ was smaller than 0.1 mM, the increase of absorbance, A with increasing ${\mathit{\rho }}_P^0$ was linear for the same initial molar concentration of BCA, ${\mathit{\rho }}_B^0$ and increased with ${\mathit{\rho }}_B^0$. However when ${\mathit{\rho }}_P^0$ was larger than 0.1 mM, the relation between A and ${\mathit{\rho }}_P^0$ became nonlinear (see insert of Fig. 2). Furthermore, maximum absorbance was reached when ${\mathit{\rho }}_P^0$ increased to 2.8 mM. When [BCA], ${\mathit{\rho }}_B^0$ was increased, the color formation was enhanced and the maximum became flatter and reached a saturation value at 19.1 to 31.9 mM ${\mathit{\rho }}_B^0$.

Fig. (2).

Absorbance of sixty sample solutions at 562 nm. The data points for the same BCA concentration, denoted by the same symbols, are connected by straight lines. Each data point was the average value of two replicates as well as standard error.

These results indicated that excess peptide bonds compete with BCA for binding cuprous ions. This competition mechanism became more significant at high protein concentration. In the light of previous reports [4-6], in which the formation of tetradentate complexes between Cu²⁺ and peptide backbone was postulated to explain redox reactions, we regarded the nearby two peptide bonds (NTPB) as a bidentate ligand that could form two new complexes with Cu¹⁺, i.e. BCA-Cu¹⁺-NTPB and NTPB-Cu¹⁺-NTPB (Fig. 1b and c). Because the maximum absorbance increased with initial BCA concentration, we concluded that the production of the chromogenic complex and other possible complexes were equilibrium processes. That it finally reached a maximum value, indicated that at that point all the cupric ions were reduced to cuprous ions.

THEORETICAL MODELING

Determination of Molar Absorption Coefficient of BCA-Cu¹⁺-BCA Complex

The relationship between the absorbance A and molar concentration ρ of a solution can be described by Lambert-Beer law, A=εlρ, where ε is the molar absorption coefficient of measured solution and l the length of the optical path of cuvette. Fig. (2) shows a flat and saturated peak region at concentrations of BCA, 19.1 mM up to 31.9 mM. It means that nearly all the Cu²⁺ was reduced to Cu¹⁺ and all the Cu¹⁺ was in the form of the chromogenic complex BCA-Cu¹⁺-BCA to give a maximum absorbance, A_b. So there is a final equilibrium state for a constant initial molar concentration of Cu²⁺, where ${\mathit{\rho }}_{B_2{C}^1}={\mathit{\rho }}_{C^1}^t={\mathit{\rho }}_{C^2}^0=0.4$mM. We can calculate the molar absorption coefficient by $\mathit{\epsilon }=A_b/\left(l{\mathit{\rho }}_{C^2}^0\right)$. From our results, the maximum absorbance is A_b = 0.312 (see Fig. 2), so ε = 7.8×10³ L·mol^-1·cm^-1. The value of Brenner et al. [7], 7.7×10³, is very close to ours.

The Relation between Cuprous Ion and Its Complexes and the Simplification at High Protein Concentration

We assume that all three cuprous complexes (see Fig. 1) exist in solution and that their formation is also controlled by their respective equilibrium processes. The equilibrium constants of every complex can be given as follows:

$$K_1={\mathit{\rho }}_{B_2{C}^1}/\left({\mathit{\rho }}_B^2{\mathit{\rho }}_{C^1}\right),K_2={\mathit{\rho }}_{{\mathit{BC}}^1{P}_2}/\left({\mathit{\rho }}_B{\mathit{\rho }}_P{\mathit{\rho }}_{C^1}\right),K_3={\mathit{\rho }}_{P_4{C}^1}/\left({\mathit{\rho }}_P^2{\mathit{\rho }}_{C^1}\right).$$ (1)

It should be noticed that during the equilibrium process of forming BCA-Cu¹⁺-NTPB and NTPB-Cu¹⁺-NTPB, NTPB is a single reactant, not similar to two discontinuous peptide bonds.

Considering the conservation of Cu¹⁺, the total concentration of Cu¹⁺ in a solution at the equilibrium state can be given as:

$${\mathit{\rho }}_{C^1}^t={\mathit{\rho }}_{B_2{C}^1}+{\mathit{\rho }}_{{\mathit{BC}}^1{P}_2}+{\mathit{\rho }}_{P_4{C}^1}+{\mathit{\rho }}_{C^1}.$$ (2)

Substituting Eq. (1) into Eq. (2), gives the dimensionless ratio:

$$\frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^1}^t}=\frac{K_1{\mathit{\rho }}_B^2}{K_1{\mathit{\rho }}_B^2+K_2{\mathit{\rho }}_B{\mathit{\rho }}_P+K_3{\mathit{\rho }}_P^2+1}.$$ (3)

The molar concentration of the complex B₂C¹ can be expressed as follows:

$${\mathit{\rho }}_{B_2{C}^1}=A/\mathit{\epsilon }l,$$ (4)

where A is the measured absorbance for a sample solution at 562nm. The path length of cuvette l is 0.1 cm in this work.

To fit the experimental results, we simplify Eq. (3) for the solution with high protein concentration after maximum absorbance is reached, where ${\mathit{\rho }}_P^0/{\mathit{\rho }}_{C^2}^0>>1,$ so the concentration of the free peptide bonds can be obtained through the following approximation of ${\mathit{\rho }}_P\approx {\mathit{\rho }}_P^0$. We hypothesize that when the concentration of protein was high, all the Cu²⁺ was reduced to Cu¹⁺, i.e. ${\mathit{\rho }}_{C^1}^t={\mathit{\rho }}_{C^2}^0$. The concentrations of BCA in our experiment were far higher than the initial concentration of copper ions, i.e. ${\mathit{\rho }}_B^0/{\mathit{\rho }}_{C^2}^0>15$, so ${\mathit{\rho }}_B\approx {\mathit{\rho }}_B^0$. Introducing the above three approximations into Eq. (3) and considering Eq. (4), we get an equation applicable to high protein concentration:

$$\frac{A}{\mathit{\epsilon }l{\mathit{\rho }}_{C^2}^0}\approx \frac{K_1{\left({\mathit{\rho }}_B^0\right)}^2}{K_1{\left({\mathit{\rho }}_B^0\right)}^2+K_2{\mathit{\rho }}_B^0{\mathit{\rho }}_P^0+K_3{\left({\mathit{\rho }}_P^0\right)}^2+1}.$$ (5)

The Determination of Equilibrium Constants by Fitting the Experimental Results at High Protein Concentration

To determine the three equilibrium constants of K₁, K₂ and K₃, the experimental data for the sample solutions with protein concentration higher than 2.8 mM was fitted to Eq. (5). As two replicates were completed for an experimental condition, we considered every replicate as an individual data point during fitting. (A bad data point for ${\mathit{\rho }}_B^0=6.18$ mM was ignored during fitting due to its abnormal deviation from the absorbance value of its replicate and other neighboring data.) Finally, we used global fitting with 49 experiment data points to determine the three constants. The software used for the analysis was Prism (Version 4.0, GraphPad Software, Inc.) and the fitting results are listed in Table 1 [8]. During a nonlinear regression, χ² denotes the sum of the squares of the vertical distances of the points from the best-fit curve. The coefficient of determination R², a fraction between 0.0 and 1.0, qualifies the goodness of fit. When R² equals 0.0, the best-fit curve fits the data no better than a horizontal line going through the mean of all Y values being determined. When R² = 1.0, all points lie exactly on the curve with no scatter, i.e. χ² = 0. ([7], page 33-34).

Table 1.

Fitting Results for Three Equilibrium Constants

	K1>0, K2>0,K3>0	K1>0, K2>0,K3=0	K1>0, K2=0,K3>0
Equilibrium constantsa, mM-2
K1	0.206±0.0468	0.220±0.0499	0.106±0.0154
K2	0.0259±0.00841	0.0302±0.00820	0
K3	0.000716±0.000858	0	0.00386±0.000836
Goodness of fit
R2	0.899	0.897	0.782
ν	46	47	47
χ2	0.0837	0.0851	0.180
χν2	0.00182	0.00181	0.00383

^aThe mean equilibrium constants were determined by fitting the experimental data for the sample solutions with high concentrations of protein with Eq. (5). Every replicate was regarded as an individual data point during fitting. Data are presented as mean ± S.D.

To judge which one of the three complexes in Fig. (1) could most probably exist, we added some constraints in the procedure of fitting. When K₁>0, K₂>0, K₃>0, which means all three complexes exist in the solution, the best-fit value of K₃ was much smaller than the other two equilibrium constants and even less than its standard deviation (see Table 1). Thus, we conclude that NTPB-Cu¹⁺-NTPB doesn’t exist. For the case that only BCA-Cu¹⁺-BCA and NTPB-Cu¹⁺-NTPB existed in the solution (K₁>0, K₂=0, K₃>0), the coefficient of determination R² was lower and the reduced sum of squares ${\mathit{\chi }}_v^2$ was greater than the other two cases, indicating a bad fit, and confirming the negligible probability of NTPB-Cu¹⁺-NTPB. Perhaps there is some NTPB-Cu¹⁺- NTPB in the solution, but too little to have any effect. When only BCA-Cu¹⁺-BCA and BCA-Cu¹⁺-NTPB existed (K₁>0, K₂>0, K₃=0), every fitting parameter was reasonable. Therefore, we concluded that the competition of peptide bonds with BCA for binding to cuprous ions was accomplished by formation of BCA-Cu¹⁺-NTPB but not NTPB-Cu¹⁺-NTPB.

If we let K₃ = 0 and make use of the approximation of ${\mathit{\rho }}_B\approx {\mathit{\rho }}_B^0$, Eq. (3) can be rewritten as:

$$\frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^1}^t}\approx \frac{K_1{\left({\mathit{\rho }}_B^0\right)}^2}{K_1{\left({\mathit{\rho }}_B^0\right)}^2+K_2{\mathit{\rho }}_B^0{\mathit{\rho }}_P+1}.$$ (6)

The Generalization of Eq. (6) for All Protein Concentration

It should be noted that the value of K₁ was about 7 times larger than K₂, so the effect of peptide bonds competing for binding to Cu¹⁺ in a solution with low protein concentration may not be significant. For a solution with low protein concentration and low BCA concentration, e.g. ${\mathit{\rho }}_P^0=1$mM and ${\mathit{\rho }}_B^0=6.18\mathrm{ mM}$, then $K_1{\left({\mathit{\rho }}_B^0\right)}^2/K_2{\mathit{\rho }}_B^0{\mathit{\rho }}_P>45$, so the approximation of ${\mathit{\rho }}_p\approx {\mathit{\rho }}_p^0$ in Eq. (6) will not affect the ratio significantly. Considering the simplified expression (5) of the ratio, ${\mathit{\rho }}_{B_2{C}^1}/{\mathit{\rho }}_{C^1}^t$ for the solutions with high protein concentration (note that $A/\mathit{\epsilon }l={\mathit{\rho }}_{B_2{C}^1}$, ${\mathit{\rho }}_{C^1}^t={\mathit{\rho }}_{C^2}^0$ and K₃ = 0), an equation (7) suitable for all solutions with different protein concentrations is as follows:

$$\frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^1}^t}\approx \frac{K_1{\left({\mathit{\rho }}_B^0\right)}^2}{K_1{\left({\mathit{\rho }}_B^0\right)}^2+K_2{\mathit{\rho }}_B^0{\mathit{\rho }}_P^0+1}.$$ (7)

An Empirical Function for the Production of Cuprous Ions

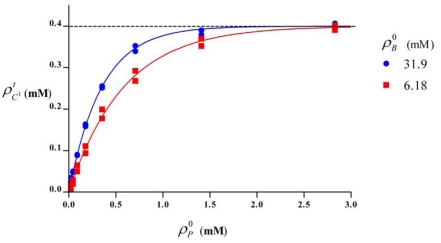
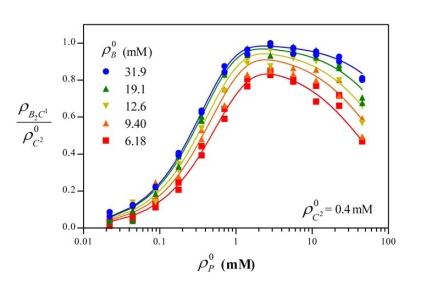
Using Eq. (7) and the determined values of K₁ and K₂, the molar concentration of total cuprous ion, ${\mathit{\rho }}_{C^1}^t$, were computed and plotted as a function of initial protein concentration ${\mathit{\rho }}_P^0$ for two constant BCA concentrations of 6.18 and 31.9 mM in Fig. (3). The curves can be described very well with an exponential function. Currently the explicit reaction equation cannot be presented for the reduction of Cu²⁺ to Cu¹⁺, so we use an empirical exponential function to describe the relation between total concentration of cuprous ions and the initial protein concentration for constant initial BCA concentration as follows:

Fig. (3).

Relation between the molar concentrations of total cuprous ions ${\mathit{\rho }}_{C^1}^t$ and the initial protein concentration ${\mathit{\rho }}_P^0$. The points were calculated by Eq. (7) from experimental data, using the determined values of K₁ and K₂ in Table 1 for two initial BCA concentrations of 6.18 and 31.9 mM. The fitted curves were calculated by Eq. (8) were also plotted (lines). The data for high protein concentration are not shown.

$$\frac{{\mathit{\rho }}_{C^1}^t}{{\mathit{\rho }}_{C^2}^0}=1-\exp \left(-b\frac{{\mathit{\rho }}_P^0}{{\mathit{\rho }}_{C^2}^0}\right).$$ (8)

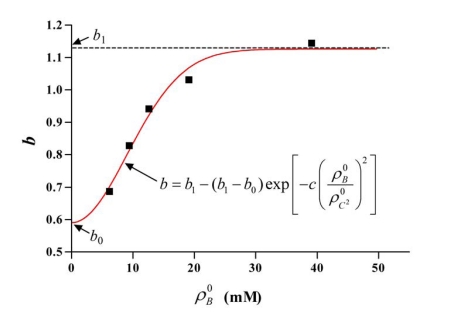
The parameter, b can be considered as an integrated equilibrium constant, which reflects the effect of some factors of amino acid composition and the initial concentrations of BCA and Cu²⁺ on the reductive reaction. For each set of experimental data with the same initial concentration of BCA, the value of b was determined by fitting it with Eq. (8), in which the dimensionless ratio ${\mathit{\rho }}_{C^1}^t/{\mathit{\rho }}_{C^2}^0$ could be obtained from the fitting result with Eq. (5) and Eq. (7). The value of b as a function of the initial concentration of BCA is plotted in Fig. (4). As expected, b increased with the initial concentration of BCA to a final constant value. We use another empirical exponential function to describe the effect of BCA concentration on b:

Fig. (4).

Parameter b fitted by Eq. (8) for the corresponding ${\mathit{\rho }}_B^0$ is denoted by the points. For constant initial concentration of Cu²⁺ (0.4mM), the variation of b with initial concentration of BCA was calculated using Eq. (9) (parameters b₀, b₁, c come from Table 2). The determined coefficient R² of each fitting was greater than 0.97

$$b=b_1-\left(b_1-b_0\right)\exp \left[-c{\left(\frac{{\mathit{\rho }}_B^0}{{\mathit{\rho }}_{C^2}^0}\right)}^2\right],$$ (9)

where c is a constant. The fitted curve is plotted in Fig. (4).

The Complete Equilibrium Equation

Finally, we obtained a complete equilibrium equation for describing the chemical reactions between protein, copper ions (Cu²⁺ and Cu¹⁺), and BCA:

$$\frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^2}^0}=\frac{{\mathit{\rho }}_{C^1}^t}{{\mathit{\rho }}_{C^2}^0}\cdot \frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^1}^t}=\left[1-\exp \left(-b\frac{{\mathit{\rho }}_P^0}{{\mathit{\rho }}_{C^2}^0}\right)\right]\left(\frac{K_1{\left({\mathit{\rho }}_B^0\right)}^2}{K_1{\left({\mathit{\rho }}_B^0\right)}^2+K_2{\mathit{\rho }}_B^0{\mathit{\rho }}_P^0+1}\right)$$ (10)

The five parameters in the above equations (9) and (10) were obtained by fitting all the experimental data (one bad data point was ignored) and the fitting results are listed in Table 2. The curves predicted by substituting the fitted parameters into the complete equilibrium equation agreed very well with the experimental data (Fig. 5). It should also be noticed that the equilibrium constants of K₁, K₂ fitted from all sample solutions (Table 2) were very close to those from high protein concentration (Table 1).

Table 2.

Fitting Results of Five Parameters in the Equilibrium Quation

Parametersa
B1	b0	c	K1, mM-2	K2, mM-2
1.12±0.0423	0.596±0.0717	0.00104±0.000320	0.198±0.0307	0.0267±0.00510
Goodness of Fit
R2	ν	χ2	χν2
0.990	114	0.135	0.00118

^aThe mean parameters were determined by fitting the experimental data for all the sample solutions with Eq. (9) and (10). Every replicate was regarded as an individual data point during fitting. Data are presented as mean ± S.D.

Fig. (5).

Comparison between the experimental results and the curve predicted by Eq. (9) and (10) using the fitted parameters. During the process of fitting, each replicate was treated as an individual data point and all of them were plotted. Points determined with the same initial concentration of BCA were denoted by the same symbol. The determination coefficient during global fitting was 0.990 and the degrees of freedom were 114.

DISCUSSION

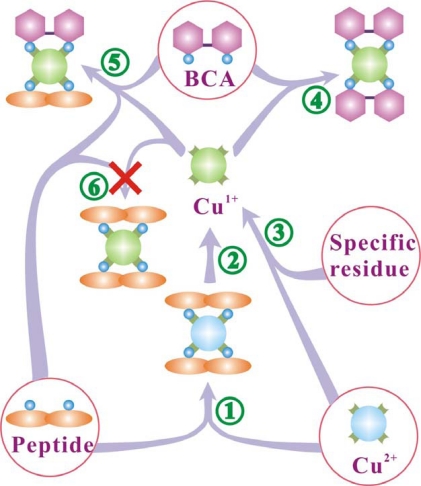
Based on experimental results, we proposed a competition of peptide bonds with BCA molecules for binding to cuprous ions and established a theoretical model to describe quantitatively the interactions between the substances in the BCA protein assay (Fig. 6). In the competition of peptide bonds with BCA for binding to cuprous ions, both tetradentate complexes of BCA-Cu¹⁺-NTPB and NTPB-Cu¹⁺-NTPB were considered as possibilities, but the fitted data indicated that only the former complex existed. The steric repulsion in the latter complex of long peptide chains might be the main reason for the inexistence of NTPB-Cu¹⁺-NTPB.

Fig. (6).

Schematic drawing to display the chemical species in a solution during the BCA protein assay. Species enclosed by a circle are the reactants. The peptide bonds and specific residues reduce cupric ions to cuprous ions, which form two complexes with peptide bonds and BCA. Peptide bonds can also form a complex with cupric ions (biuret reaction).

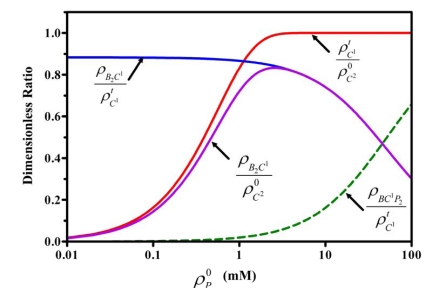
The nonlinear relation between the protein concentration and the color production limits the measurement range of the BCA protein assay. The linear working range of the assay kit (23235#) is below 20 µg/mL. Although another assay kit from Pierce, (23225#) is claimed to be able to determine protein concentration in the range, 20 to 2000 µg/mL, its real maximum measurement limit is only about 100 µg/mL because in its procedure, the sample is diluted, one part with 20 parts of working reagent giving a 21-fold dilution. Therefore understanding the character of the nonlinearity will be helpful in extending the measurement of the BCA protein assay to higher protein concentrations. According to our results, the nonlinearity is caused by two factors, i.e. the reduction of Cu²⁺ and the competition of peptide bonds with BCA for binding to Cu¹⁺. By giving a constant initial concentration of BCA, ${\mathit{\rho }}_B^0=6.18\mathrm{ mM}$, we plotted the curves of four dimensionless ratios, ${\mathit{\rho }}_{B_2{C}^1}/{\mathit{\rho }}_{C^2}^0,{\mathit{\rho }}_{C^1}^t/{\mathit{\rho }}_{C^2}^0,{\mathit{\rho }}_{B_2{C}^1}/{\mathit{\rho }}_{C^1}^t\mathit{ and }{\mathit{\rho }}_{{\mathit{BC}}^1{P}_2}/{\mathit{\rho }}_{C^1}^t$, with respect to ${\mathit{\rho }}_P^0$ in Fig. (7) and noted that $\frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^2}^0}=\frac{{\mathit{\rho }}_{C^1}^t}{{\mathit{\rho }}_{C^2}^0}\cdot \frac{{\mathit{\rho }}_{B_2{C}^1}}{{\mathit{\rho }}_{C^1}^t}$. It could be seen that for a low initial protein concentration, since ${\mathit{\rho }}_{B_2{C}^1}/{\mathit{\rho }}_{C^1}^t$ was almost constant, it was the nonlinearity of the reduction reaction, but not the competition mechanism that dominated the nonlinearity of the color production. But at high protein concentrations, since ${\mathit{\rho }}_{C^1}^t/{\mathit{\rho }}_{C^2}^0$ was almost equal to 1 and ${\mathit{\rho }}_{{\mathit{BC}}^1{P}_2}/{\mathit{\rho }}_{C^1}^t$ increased dramatically, the reduction reaction was complete and the competition caused the nonlinearity of color formation.

Fig. (7).

Interpretation of the appearance of the nonlinearity and plateau of the absorbance with increasing initial protein concentration. Four dimensionless ratios were plotted and the calculation conditions were: ${\mathit{\rho }}_B^0=6.18\mathrm{ mM}$, ${\mathit{\rho }}_{C^2}^0=0.4\mathrm{ mM}$, $b_1=1.12$, $b_0=0.596$, $c=0.00104$, $K_1=0.198{\mathrm{ mM}}^{-2}$, $K_2=0.0267{\mathrm{ mM}}^{-2}$

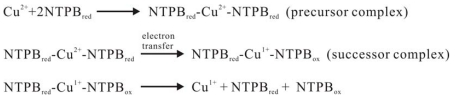
But in establishing the theoretical model to quantitatively describe the whole equilibrium reaction, there are still some issues that should be discussed. We used an empirical function to describe the reduction of Cu²⁺ to Cu¹⁺ by peptide bonds This fitted the experimental data very well but its physical meaning was still obscure because the reductive reactions were complicated. There have been few studies of these reactions [4-6]. It was demonstrated that NTPB and four specific amino acids, cysteine, cystine, tryptophan and tyrosine were the reductive groups in the BCA assay. In both the Lowry [9] and BCA methods, the Cu²⁺ ion must form a tetradentate complex with the peptide backbone to oxidize the peptide bond. Presumably, the reduction by peptide bonds is a three-step process (Fig. 8). First, the cupric ion forms a precursor complex NTPB-Cu²⁺-NTPB with some groups on the peptide backbone. Second, electron transfer occurs inside the precursor complex and Cu²⁺ is reduced to Cu¹⁺, then a successor complex NTPB-Cu¹⁺-NTPB forms. Finally, the successor complex dissociates and the cuprous ion can be detected by BCA or other reagent. But we know that there is still a long way to clarify the reductive process.

Fig. (8).

Proposed three-step reduction reaction of Cu²⁺ to Cu¹⁺ by peptide bonds: 1) the cupric ion forms a precursor complex NTPB-Cu²⁺-NTPB with groups on the peptide; 2) Electron transfer occurs inside the precursor complex, reducing Cu²⁺ to Cu¹⁺; 3) The successor complex dissociated.

It should be noted that in the simplified model, ${\mathit{\rho }}_B\approx {\mathit{\rho }}_B^0$ is a basic hypothesis, so this model is restricted to the case of ${\mathit{\rho }}_B^0>>{\mathit{\rho }}_{C^2}^0$ (in our experiments, ${\mathit{\rho }}_B^0>15{\mathit{\rho }}_{C^2}^0$). The error caused by this approximation can be estimated. In most cases, the relative error of ${\mathit{\rho }}_{B_2{C}^1}/{\mathit{\rho }}_{C^2}^0$ calculated by Eq. (9) and Eq. (10) is less than 5%, which is acceptable in experiment. If the mechanism of the reduction reaction and the contribution of peptide bonds to the production of cuprous ions are clarified, the accurate model can be deduced from a series of equilibrium equations and conservation equations.

Based on the above discussion, adding more cupric ions would increase the linear working range, in which ${\mathit{\rho }}_P^0/{\mathit{\rho }}_{C^2}^0<<1$. When applying the model established in this paper to measure the concentration of a protein in the nonlinear working range, the parameter b must be determined, as it is dependent on the amino acid composition and thus is variable from protein to protein.

CONCLUSIONS

Using the micro BCA protein assay kit of the Pierce Company and varying the concentration of BCA, we measured the absorbance at 562 nm with varying concentrations of BSA. To explain the nonlinearity of the color formation with increasing protein concentration and the plateau value at high protein concentrations, we considered the competition of peptide bonds with BCA for binding to cuprous ions, assuming that there might exist two new complexes besides the chromogenic complex. For the limiting condition of ${\mathit{\rho }}_B^0/{\mathit{\rho }}_{C^2}^0>>1$, that is when [BCA] was in excess of copper ions, a simplified model was presented to describe the concentrations of, protein, copper ions, BCA and their complexes at equilibrium. The parameters in the equation were fitted with experimental data, and the curves predicted by the equilibrium equation coincided well with experimental results. The experimental results and theoretical model indicated that the peptide bonds that are not involved in the reduction reaction compete with BCA for binding to cuprous ions. In addition to the chromogenic complex of BCA-Cu¹⁺-BCA, there was evidence for the formation of a new complex of BCA-Cu¹⁺-NTPB. Another possible complex of NTPB-Cu¹⁺-NTPB was shown to be negligible based on the fitting results. The mechanism of the reduction reaction is still unknown but an empirical exponential function with three parameters could describe the production process of cuprous ions quantitatively. The parameters may be dependent on the amino acid composition of a protein and further work should be done to clarify quantitatively the reduction reaction. This work partially clarified the mechanisms of interaction between protein, copper ions and BCA in the BCA protein assay and explained the nonlinearity of absorbance at high protein concentration. The affinity of protein for cuprous ions may be the basis of further investigation of redox reactions in protein-copper systems and the design of new protein assay methods.

GLOSSARY

A

 = absorbance at 562 nm

b

 = equilibrium constant of reductive reaction of Cu²⁺ to Cu¹⁺

b₁

 = upper limit of b

b₀

 = lower limit of b

c

 = parameter describing the effect of concentration of BCA on b

K₁

 = equilibrium constant of BCA-Cu¹⁺-BCA complex

K₂

 = equilibrium constant of BCA-Cu¹⁺-NTPB complex

K₃

 = equilibrium constant of NTPB-Cu¹⁺-NTPB complex

l

 = optical length path of cuvette

R²

 = coefficient of determination

ε

 = molar absorption coefficient

ρ_x

 = molar concentration of substance x at the equilibrium state

${\mathit{\rho }}_x^0$

 = initial molar concentration of substance x

${\mathit{\rho }}_x^t$

 = total molar concentration of substance x

χ²

 = chi squares statistics

${\mathit{\chi }}_v^2$

 = reduced chi squares statistics (=χ²/v)

ν

 = number of degrees of fitting freedom

ABBREVIATION FOR THE SUBSTANCE IN EXPRESSION OF CONCENTRATION

B

 = bicinchoninic acid (BCA)

C¹

 = cuprous ion (Cu¹⁺)

C²

 = cupric ion (Cu²⁺)

P

 = peptide bond

B₂C¹

 = BCA-Cu¹⁺-BCA complex

BC¹P₂

 = BCA -Cu¹⁺-NTPB complex

P₄C¹

 = NTPB-Cu¹⁺-NTPB complex