Increased Course Structure Improves Performance in Introductory Biology

Abstract

We tested the hypothesis that highly structured course designs, which implement reading quizzes and/or extensive in-class active-learning activities and weekly practice exams, can lower failure rates in an introductory biology course for majors, compared with low-structure course designs that are based on lecturing and a few high-risk assessments. We controlled for 1) instructor effects by analyzing data from quarters when the same instructor taught the course, 2) exam equivalence with new assessments called the Weighted Bloom's Index and Predicted Exam Score, and 3) student equivalence using a regression-based Predicted Grade. We also tested the hypothesis that points from reading quizzes, clicker questions, and other “practice” assessments in highly structured courses inflate grades and confound comparisons with low-structure course designs. We found no evidence that points from active-learning exercises inflate grades or reduce the impact of exams on final grades. When we controlled for variation in student ability, failure rates were lower in a moderately structured course design and were dramatically lower in a highly structured course design. This result supports the hypothesis that active-learning exercises can make students more skilled learners and help bridge the gap between poorly prepared students and their better-prepared peers.

INTRODUCTION

In 1920, <4% of the U.S. population went to college (Ratcliff, 2010). Now, >55% of the general population over the age of 25 has at least some college experience (U.S. Census Bureau, 2009). In the United States, the democratization of higher education began with the founding of the land grant (public) universities in the 1860s, continued with the founding of community colleges in the early 1900s, accelerated with the G.I. Bill that passed in 1944, and culminated with the expansion of the women's movement and a long-delayed end to exclusion based on race in the 1960s and 1970s (Eckel and King, 2006). Indeed, increased access to higher education is occurring internationally (e.g., Scott, 1995).

For faculty, the democratization of higher education means that an increasingly smaller percentage of students come from privileged social and economic backgrounds. Although faculty should celebrate this fact, it is common to hear instructors express concern about the downside of democratization: high variation in student ability and preparedness. Data from the ACT (2006), for example, suggest that 49% of high school students who took the ACT college entrance exam in 2005 were not ready for college-level reading.

How can we help underprepared but capable students succeed, while continuing to challenge better-prepared students? The issue is particularly acute in gateway courses—the large, introductory classes that undergraduates take in their first or second year. Across the science, technology, engineering, and mathematics (STEM) disciplines, failure rates in these courses can be high—even in moderately and highly selective schools, where students are “prescreened” on the basis of academic capability. Although we are not aware of a comprehensive review, it appears common for one-third of students to fail in STEM gateway courses (Table 1).

Table 1.

Failure rates in some gateway STEM courses

Field	Course	Failure rate	Failure criterion	Reference
Biology	Intro-majors	56%	Average proportion of Ds and Fs on exams	Burrowes, 2003
	Intro-majors	>25%	Course outcome: D, F, or drop	Wischusen and Wischusen, 2007
	Intro-nonmajors	27%	Course outcome: D, F, or drop	Marrs and Chism, 2005
	Biochemistry	85%	F on first exam	Peters, 2005
	Medical Microbiology	30%	Course outcome: D or F	Margulies and Ghent, 2005
Chemistry	Intro-majors	∼50%	Course outcome: D, F, or drop	Reardon et al., 2010
	Intro-nonmajors	≥ 30%	Course outcome (“at most institutions”): fail or drop	Rowe, 1983
Computer science	Intro to programming	33%	Course outcome (international survey): F or drop	Bennedsen and Casperson, 2007
Engineering	Intro to chemical engineering	32%	Course outcome: D, F, or drop	Felder et al., 1998
Mathematics	First-year calculus	42%	Course outcome (U.S. national average): failure	Treisman, 1992
Physics	Intro-majors	33%	Course outcome: D, F, or drop	Marrs and Chism, 2005

Failure has grave consequences (Wischusen and Wischusen, 2007). In addition to the emotional and financial toll that failing students bear, they may take longer to graduate, leave the STEM disciplines, or drop out of school entirely. Analysts have been particularly concerned that underrepresented minorities (URMs) and other students who quit the STEM disciplines take valuable perspectives and creativity with them (Seymour and Hewitt, 1997). Students who repeat gateway courses also add pressure on enrollments—in some cases, denying places to students who want to take the course for the first time.

How can we reduce failure rates in STEM courses, without reducing rigor? Recent research suggests that changes in course design—specifically, the introduction of active-learning strategies—can help. For example, Beichner et al. (2007) reported that changing to workshop (or studio) models of instruction, which emphasize collaborative group work in class, cut failure rates by 40–60% in introductory physics across a range of institutions. Similarly, Lasry et al. (2008) found that the use of peer instruction with clickers (see Mazur, 1997) reduced the drop rate in introductory physics at a community college and at a research university by factors of two to three.

We hypothesized that intensive active learning, combined with frequent formative assessment, can lower failure rates in an introductory biology course for majors. Previously we reported an average increase of 3–4% on exam scores and a 30% reduction in failure rate when we introduced active-learning exercises that were graded (Freeman et al., 2007). Subsequently we have introduced additional active learning exercises in an attempt to increase exam performance and reduce the failure rate even further. The result is what we term a highly structured course design. Low-structure courses are based on traditional lecturing and high-stakes assessments—typically two or three midterms and a comprehensive final exam. In contrast, highly structured courses assign daily and weekly active-learning exercises with the goal of providing constant practice with the analytical skills required to do well on exams.

If highly structured courses lower failure rates, faculty might find their increasingly diverse student population a source of reward and inspiration, rather than frustration. But do highly structured courses work? Do they lead to greater success and fewer failures? Testing the highly structured course design hypothesis requires that instructor identity, exam difficulty, and student ability be controlled across the classes being studied.

METHODS

Course Background

This research focused on students in Biology 180, the first in a three-quarter introductory biology sequence designed for undergraduates intending to major in biology or related disciplines at the University of Washington (UW). The course introduces evolution, Mendelian genetics, diversity of life, and ecology. The course is offered every quarter; in the 2009–2010 academic year, total enrollment approached 2100.

Although the course is usually team-taught, the data analyzed here come from six quarters when one of the authors (S.F.) was the sole instructor of record. Throughout the study, the course was offered for five credits and included four 50-min class sessions and a 2- or 3-h laboratory each week. In every quarter there were 400 exam points possible; all exam questions were written—most were short-answer, but some involved graphing, computation, or labeling diagrams.

Student Demographics

During the study period, most students had to complete a chemistry prerequisite before registering for Biology 180; the majority were in their sophomore year. In the most recent quarter analyzed here, the course's demographic makeup was 61.1% female and 38.9% male; 46.7% Caucasian, 38.5% Asian-American, and 7.4% URM (African-American, Hispanic, Native American, or Pacific Islander), with 7.4% of students declining to declare their ethnicity. In addition, 16.4% of the students were in the UW Educational Opportunity Program, meaning that they were identified as economically or educationally disadvantaged. These demographic data are typical across the quarters and years of the study.

Course Design

During the six quarters analyzed in this study, the instructor used various combinations of teaching strategies, detailed here in order of implementation.

• Socratic lecturing involved frequent use of questions posed to the class, with answers solicited from students who raised their hands. In addition to calling on “high responders,” wider participation was encouraged by use of think/pair/share (Lyman, 1981), asking for a response from students in a particular section of the room, or asking for a response from a student who had not contributed before. The intent of Socratic lecturing was to engage student attention and provide feedback to the instructor.

• Ungraded active-learning exercises encouraged active participation in class. The exercises used were minute papers (Mosteller, 1989; Angelo and Cross, 1993; Boyd, 2001), case studies with question sets completed by informal groups (Yadav et al., 2007), writing answers to exam-style questions followed by discussion, and in-class demonstrations with student participation (Milner-Bolotin et al., 2007). In most cases, each class session involved at least three such exercises. The intent of the ungraded exercises was to give students practice with the higher-order cognitive skills required to do well on exams.

• Clicker questions were multiple-choice questions presented in class; students responded with a personal response device or “clicker” (Caldwell, 2007). Clicker questions were implemented in a peer instruction format, where individuals answered on their own and then reanswered after discussion with one or more students seated next to them (Mazur, 1997; Smith et al., 2009). The instructor asked three to five clicker questions per class session; in most cases, a maximum of three clicker points was possible each class session, assigned for right/wrong responses (see Freeman et al., 2007). Typically, clicker questions summed to ∼12% of the total course points. The intent of the clicker questions was to develop student thinking at the application and analysis level and encourage peer teaching.

• Practice exams were online, weekly, peer-graded exercises where students submitted written responses to exam-style questions. Students were given 35 min to respond to five short-answer questions. After answers were submitted, software developed in our department randomly and anonymously gave each student a set of answers to grade, along with sample answers and grading rubrics (Freeman et al., 2007; Freeman and Parks, 2010). At two points per question, there were 10 points possible each week—representing ∼8% of the total course grade. The intent of the exercises was to give students practice with answering high-level, exam-style, written questions under time pressure, but in a low-stakes environment.

• Class notes summaries were weekly assignments that required students to state the three most important concepts introduced each day in lecture, along with a question based on the idea that they understood least well in that class session. The summaries were filled out online and were due each Monday morning. Students were given a course point per week for participation, with a five-point bonus for completing the exercise every week of the course—for a total of ∼2% of total course points. The objectives of class notes summaries were to help students 1) organize and synthesize their course material, and 2) increase metacognition—specifically, the ability to identify which information is most important and which concepts are understood most poorly (Bransford et al., 2000).

• Reading quizzes opened every afternoon after class and closed the morning of the next class (Novak et al., 1999; Crouch and Mazur, 2001). They consisted of 5–10 multiple-choice questions, delivered and corrected via an online quizzing system, and tested understanding of basic vocabulary and concepts. The exercises were open-book and open-note; students were free to do them in groups or individually. Typically, the two-point reading quizzes summed to ∼8% of total course points. The intent of the reading quizzes was to make students responsible for learning basic course content on their own and prepare them to work on higher-order cognitive skills in class.

• In-class group exercises involved informal groups of three or four students sitting adjacent to one another. The exercises consisted of one to three exam-style questions on the topic currently being discussed in class (Farrell et al., 1999; Eberlein et al., 2008). As students discussed the questions, graduate and peer teaching assistants (TAs) moved around the lecture hall to monitor the conversations and answer queries from students. Although no course points were awarded during these activities, participation was encouraged because the instructor closed the small-group discussions and then called on students, from a randomized class list, to solicit student responses in front of the entire class. Typically, a single 50-min class session included five or six group exercises, with 12–15 students called on each day. These class sessions, then, consisted of a series of 3- to 5-min mini-lectures that introduced or discussed either a clicker question or a group exercise. These sessions differed dramatically from the ungraded active-learning exercises introduced before, for two reasons: There were more than double the number of activities per class session, and participation—“enforced” by random-call versus calling on volunteers—appeared much higher. The intent of the group exercises was to help students develop higher-order cognitive skills, with peer and TA feedback, in a low-stakes environment.

Over the six quarters in the study—when the same instructor taught the course—the courses can be placed into three categories: 1) relatively low structure in Spring 2002 and Spring 2003; 2) moderate structure, due to the addition of clickers and practice exams, in Spring 2005 and Autumn 2005; and 3) high structure, due to the addition of reading quizzes, along with the substitution of in-class group exercises for Socratic lecturing, in Autumn 2007 and Autumn 2009 (Table 2).

Table 2.

Variation in course format

	Spring 2002	Spring 2003	Spring 2005	Autumn 2005	Autumn 2007	Autumn 2009
Class size (10-d class list)	331	345	Two sections of 173a	Two sections of 173a	342	699
Elements of course design
Socratic lecturing	X	X	X	X
Ungraded active learning		X
Clickers			Xb	Xc	X	X
Practice exams			Xd	Xe	Xd	Xe
Reading quizzes					X	X
Class notes summaries					X
In-class group exercises					X	X
Exams	Two 100-point midterms, 200-point comprehensive final	Two 100-point midterms, 200-point comprehensive final	Two 100-point midterms, 200-point comprehensive final	Two 100-point midterms, 200-point comprehensive final	Two 100-point midterms, 200-point comprehensive final	Four 100-point exams
Total course points	550	550	720b; 620	720	793	741

^aThe sections were taught back-to-back, with identical lecture notes. They took similar or identical midterms and an identical final exam.

^bOne section answered questions with clickers; one section answered identical questions with cards (see Freeman et al., 2007). Card responses were not graded.

^cIn one section, clicker questions were graded for participation only; in one section, identical clicker questions were graded right/wrong (see Freeman et al., 2007).

^dAt random, half the students did practice exams individually; half did the same exercise in a four-person group structured by predicted grade.

^eAll students did practice exams individually.

Several other observations are noteworthy: 1) The Spring and Autumn 2005 sections were involved in experiments on the use of clickers versus cards and grading clicker questions for participation versus right/wrong (see Freeman et al., 2007); 2) the Spring 2005 and Autumn 2007 sections were involved in experiments on individual versus group work on practice exams; 3) course enrollment varied widely, from 173 students per section to 700; 4) the exam number changed in Autumn 2007 due to increased enrollment—with two 100-point exams, spaced several weeks apart, replacing a comprehensive, 200-point final. The short-answer format for exams remained the same, however.

Computing Final Grades

Across the introductory biology series at UW, instructors strive to implement the following system for computing final grades: 1) total course points are summed for each student, 2) students with the top 5% of total course points earn a 4.0, 3) the instructor sets a level for passing the course (receiving a 0.7, and thus course credit toward graduation) that typically represents ∼50% of total course points and 40–45% of total exam points, and 4) the range of course points between the 0.7 and 4.0 cutoffs is divided into equal bins and assigned 0.8, 0.9, 1.0, and so on, up to 3.9.

During the years included in this study, students had to receive a course grade of at least 1.5 on a 4.0 scale to register for the next course in the series. Thus, we define failure as a final course grade of <1.5. Except when noted, the analyses reported here include only those students who received a grade—meaning that students who dropped the course before the final exam were not included. The data sets also excluded a small number of students who had been caught cheating.

Exam Equivalence across Quarters

In a longitudinal study that evaluates changes in failure rates, it is critical to test the hypothesis that changes in failure rates were due to changes in exam difficulty. In the Freeman et al. (2007) study, this hypothesis was tested by comparing student performance on an identical midterm in two quarters that differed in course design. Because we wanted to avoid giving an identical exam again, we created two methods for evaluating exam equivalence across the six quarters.

Weighted Bloom's Index.

Bloom's taxonomy of learning (Bloom et al., 1956; Krathwohl, 2002) identifies six levels of understanding on any topic. Bloom's framework has been applied in an array of contexts in undergraduate biology education (Crowe et al., 2008), including characterizing exams (Zheng et al., 2008). We used the six levels to create a Weighted Bloom's Index, which summarizes the average Bloom's level of exam questions weighted by the points possible:

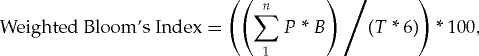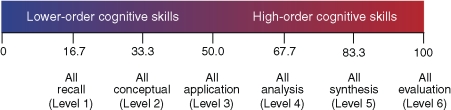
where n is the number of questions, P is points/question, B = Bloom's rank (1–6) for that question, T is total points possible, and 6 is the maximum Bloom's score. To help interpret the index, note that Level 1 and 2 questions test lower-order cognitive skills, Level 3–6 questions assess higher-order cognitive skills (Bloom et al., 1956; Krathwohl et al., 2002) and specific Weighted Bloom's Index values (Figure 1) conform to each Bloom's level, as follows:

• 16.7 is an exam with exclusively recall questions (Bloom's Level 1);

• 33.3 is an exam with exclusively conceptual understanding questions (Bloom's Level 2);

• 50 is an exam with exclusively application questions (Bloom's Level 3);

• 66.7 is an exam with exclusively analysis questions (Bloom's Level 4);

• 83.3 is an exam with exclusively synthesis questions (Bloom's Level 5); and

• 100 is an exam with exclusively evaluation questions (Bloom's Level 6).

Figure 1.

The Weighted Bloom's Index “Scale.” The Weighted Bloom's Index can be interpreted by comparing indices from actual exams to the values shown here, which are expected if all exam questions were at a certain level in Bloom's taxonomy of learning. Levels 1 and 2 in Bloom's taxonomy are considered lower-order cognitive skills; Levels 3–6 are considered higher-order cognitive skills.

We calculated a Weighted Bloom's Index for every exam in the study by recruiting three experienced TAs to assign a Bloom's level to every exam question given in each quarter. The raters were trained in “Blooming” exams by one of the authors (M.P.W.) and assessed questions that were presented in a common format and in random order. Although raters knew that they were assessing Biology 180 exam questions, they were blind to the quarter and year. They were also blind to the study's intent and to the hypothesis being tested by the ratings. Point values for each question were omitted to avoid any bias introduced by high- versus low-point-value questions. Because multipart questions are common on these exams, each rater gave a Bloom's rating to each question part. Each rater assessed 295 exam questions and assigned a total of 724 Bloom's levels. (Including the identical exam, there were a total of 310 exam questions and 750 Bloom's rankings in the study.)

We used the decision rules published by Zheng et al. (2008) to arrive at a single Bloom's level for each question part. Briefly, the three raters achieved consensus on 53 rankings during “norming sessions,” where questions were discussed as a group after being rated individually. None of the subsequent questions were discussed as a group to resolve conflicts in ratings. Instead, we assigned the consensus rating when all three raters agreed and the majority-rule rating when two of three raters agreed. When ratings were sequential (e.g., 2–3–4), we assigned the middle value. When ratings were nonsequential (e.g., 1–2–4), we assigned the arithmetic average. To assess the degree of agreement among the multiple raters, we calculated Krippendorff's alpha—an appropriate measure for ordinal coding data from multiple raters (Hayes and Krippendorff, 2007)—and the intra-class r.

The Weighted Bloom's Index should accurately summarize the average Bloom's ranking of exams, facilitating comparisons across courses or even institutions. In addition, it should contain information on exam difficulty because students typically perform much better on lower-level versus higher-level questions (e.g., Knecht, 2001; Freeman and Parks, 2010). Thus, exams with higher Weighted Bloom's Indices should be harder.

Predicted Exam Score.

As an alternative method for assessing exam difficulty, we created a Predicted Exam Score (PES) by recruiting three experienced TAs—different from the individuals who did the Bloom's ratings—to predict the average number of points that students would receive on each part of each exam question in the study. These individuals were experienced graders: In addition to running labs and attending every class, each TA in Biology 180 spends ∼40 h grading exams. Thus, the PES raters judged the difficulty of exam questions based on 1) an understanding of what had been presented in the textbook and introduced in class and 2) extensive grading experience that made them alert to wording, context, level, and other issues that cause confusion or difficulty. All three PES raters were peer TAs—senior undergraduate biology majors. We hypothesized that peer TAs might be more attuned to how undergraduates read and respond to exam questions than faculty are.

The PES raters used the same randomized list of 295 identically formatted exam questions as did the Bloom's raters, except that point values for each of the 724 question parts were indicated. Like the Bloom's raters, the PES raters were blind to the study's intent and the hypothesis being tested with the predicted-points data.

Work on the PES began with a norming session. This meeting started with each of the three individuals assigning a predicted-average-points value to 25 questions—a total of 58 question-parts—on his or her own. The three then met to discuss their predictions for average points on each question-part until they arrived at a consensus value. Subsequent questions were assessed individually but not discussed. To arrive at a single predicted-average-points value for each of the exam-question parts after the norming session, we computed the arithmetic average of the three ratings submitted.

The goal of the PES was to test the hypothesis that changes in failure rates were due to changes in the difficulty of exams, independent of changes in course design. The metric should be useful because it is reported in units of average expected points on exams and because exam points predict most of the variation in final grade (see Results).

Note that because the Weighted Bloom's Index and the PES were computed from data on all exam questions in the study, there was no sampling involved. As a result, there is no sample variance on the data reported here, and it was not possible to use statistical approaches to assess “significance” when comparing data from different exams. In cases like this, significance is a judgment about the relevance of observed differences to the hypothesis being tested.

Exam Impact on Final Course Grade

A proponent of low-structure course designs could argue that failure rates decline in highly structured courses not because of increased student learning, but because the “practice” exercises (reading quizzes, clicker questions, etc.) are easier than actual exam questions and thus inflate student performance. In addition, even in the most highly structured course designs, our intent was for exams to remain the primary determinant of final course grade—because exams represent the most controlled type of assessment possible and because exams are the major type of assessment in subsequent courses.

To test the point-inflation hypothesis, we performed simple linear regressions with each student's total exam points in each quarter as the predictor variable and his or her final grade as the response variable. In addition, we computed the 1.5 (failing) cutoff predicted by the regressions. These 1.5 cutoffs represented the average total exam points required to progress in the major, each quarter.

If exams are the major determinant of final grades irrespective of degree of course structure—even when many nonexam points are possible—then R² values for the regressions should be uniformly high, the slopes and intercepts of the regression lines should be indistinguishable, and the 1.5 cutoffs should be similar across quarters. It was not possible to use analysis of covariance (ANCOVA) to test for heterogeneity of regression slopes and intercepts across quarters because final grades were not normally distributed (Shapiro-Wilks normality test W = 0.9361, p ≪ 0.001). Rather, the best-fit distribution followed a binomial error distribution. Consequently, we used analysis of deviance to formally test the hypothesis that the slopes and intercepts of the regressions did not vary across quarters, using a Generalized Linear Model (GLM) framework (Crawley, 2007, p. 516). More specifically, we compared the fit among three linear models 1) incorporating only the covariate exam points, 2) additionally incorporating quarter as a fixed effect, and 3) the full model with an interaction term. If the additional explanatory variable and the interaction term failed to improve the fit of the GLM, it provides assurance that slopes and intercepts are homogeneous across quarters (are not significantly different, using a likelihood ratio test [LRT]).

Student Equivalence across Quarters

In a longitudinal study of student performance in courses, it is critical to test the hypothesis that changes in failure rates are due to changes in the academic ability and preparedness of the student population at the time of entering each course. To test this hypothesis, we used the Predicted Grade model introduced by Freeman et al. (2007). Briefly, we predicted a final course grade for each student in each quarter by using a regression model based on UW grade point average (GPA) and SAT-verbal scores (Predicted grade = (0.00291 × SATverbal) + (1.134 × UWGPA) – 2.663). Students who lacked an SAT-verbal score were assigned the average SAT-verbal score from that quarter; on average, 10% of students had a missing SAT-verbal score each quarter. Because the percentage of missing values was low and the loading of SAT-verbal in the regression model is small, the missing values should have a minimal impact on the analysis. In addition, analysis of variance (ANOVA) showed no heterogeneity among quarters in the UW GPAs of students with missing SAT-verbal scores (F = 0.46, df = 5, 228, p = 0.81). Thus, the substitution for missing values should not bias tests for differences in predicted grade across quarters. Because UW GPA has a large impact in the regression model, grades of students who lacked a UW GPA at the start of the course were dropped from the predicted grade analysis.

We performed linear regressions to compare the Predicted Grade with Actual Course Grade in each quarter of the study, and then used analysis of deviance to assess the robustness of the Predicted Grade model across quarters. Specifically, the analysis used a χ² test to evaluate differences between GLMs that incorporated the additional explanatory variable quarter, also incorporated an interaction term with quarter, or included no interaction term. Again, an LRT is used to compare the fit among models; failure to improve the fit of the simplest model provides assurance that slopes and intercepts are homogeneous. To test the hypothesis that students were of equivalent ability and preparedness, we used ANOVA to compare average student Predicted Grade across quarters.

In this and other statistical analyses, we checked the assumptions of the statistical tests used. Analyses were done in Excel and the R statistical environment (R Development Core Team, 2008).

RESULTS

Exam Equivalence

The TAs who ranked questions on Bloom's taxonomy showed a high level of agreement. At least two of the three raters agreed on the identical Bloom's level for 85% of the questions rated. Using the original values assigned for the norming session questions—not the consensus values—the Kippendorf's alpha among raters was 0.48 for the entire data set; the intra-class r was 0.481 (F = 4.07, df = 668, p ≪ 0.0001).

There was also a high level of agreement among the three TAs who evaluated exam questions for the PES values. Using the original values assigned for the norming session questions—not the consensus values—the intra-class r for the entire data set was 0.84 (F = 24.3, df = 725, p ≪ 0.0001).

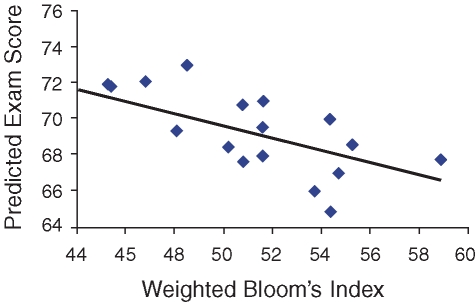
There is a strong association between the Weighted Bloom's Indices (Table 3b) and the PES values (Table 3c): The r for the 18 exams in the study (excluding one iteration of the repeated exam) is –0.72, and a regression analysis shows that variation in the Weighted Bloom's Index explains 51% of the variation in the PES (Figure 2; F = 16.7, df = 1,16, p < 0.001).

Table 3.

Exam equivalence analyses

		Independent ratings
	Discussed- consensus	All three agree	Two of three agree	Sequential ratings	Nonsequential ratings
a. Percentage agreement among Bloom's taxonomy raters.
Percentage of total ratings	7.3	26.4	51.1	9.9	5.2
“Discussed-consensus” means that questions were rated independently and then discussed to reach a consensus; “Independent ratings” were not discussed among raters. “Sequential ratings” were questions that received three ratings that differed by one Bloom's level (e.g., a 2, 3, and 4); “Nonsequential ratings” were questions that received three ratings that differed by more than one Bloom's level (e.g., a 2, 3, and 5).
b. Weighted Bloom Indices
	Spring 2002	Spring 2003	Spring 2005	Autumn 2005	Autumn 2007	Autumn 2009
Midterm 1	50.8	48.5	45.3	58.9	54.4	53.7
Midterm 2	36.1	51.6a	51.6a	46.8	50.8	54.7
Midterm 3						50.2
Final (or Midterm 4)	48.1	54.3	45.4	51.6	51.6	55.3
Course averageb	45.8	52.1	46.9	52.2	52.1	53.5
c. PES values (predicted percent correct)
	Spring 2002	Spring 2003	Spring 2005	Autumn 2005	Autumn 2007	Autumn 2009
Midterm 1	70.8	73.0	71.9	67.8	64.9	66.0
Midterm 2	73.0	68.0a	68.0a	72.1	67.7	67.0
Midterm 3						68.5
Final (or Midterm 4)	69.4	70.0	71.8	71.0	69.6	68.6
Course averageb	70.6	70.2	70.9	70.5	68.0	67.5

^aIdentical exams.

^bCourse averages were computed from data on all exam questions from that quarter. (They are not the averages of the indices from each exam.)

Figure 2.

Weighted Bloom's Indices and PES values are negatively correlated. The Weighted Bloom's Index summarizes the average Bloom's level per point on an exam; the PES summarizes expert-grader predictions for average points that a class will receive on an exam. Regression statistics are reported in the text.

Exam Impact on Course Grade

R² values indicate that, even in the most highly structured versions of the course, when exam points represented as little as 55% of the total course points, total exam points still explained 89% of the total variation in final grade (Table 4a). Across quarters in the study, the regressions of total exam points on final grade were similar, and the average number of exam points required to get a 1.5 varied little—the range was only nine points (Table 4b). In addition, analysis of deviance (Table 4b) indicated no statistically significant variation among quarters in how well total exam points predicted final grade.

Table 4.

Regression analyses: Total exam points as a predictor of final course grade. Data from the two sections in Spring 2005 were analyzed separately because the clickers and card sections in that quarter (see Materials and Methods and Table 2) had different total course points and thus a different scale for computing final grade.

a. Regression statistics
	Low structure		Moderate structure			High structure
	Spring 2002	Spring 2003	Spring 2005 (no clickers)	Spring 2005 (clickers)	Autumn 2005	Autumn 2007	Autumn 2009
Adjusted R2	0.96	0.95	0.97	0.88	0.96	0.89	0.89
y-intercept	−2.29a	−2.35a	−2.12	−2.30a	−2.57	−2.32a	−2.71
β	0.0184b	0.0186b	0.0172	0.0180b	0.0189b	0.0187b	0.0198
1.5 cutoff predicted by regression	206.4	206.6	210.1	211.1	215.8	204.0	213.0
n	323	335	174	156	333	336	653
b. ANCOVA fit by GLMs incorporating the effect of exam points, quarter, and the interaction term exam points by quarter; the response variable is actual grade (GLM with binomial error distribution). Analysis of deviance shows that slope and intercept do not significantly vary across quarter.
Model	Residual df	Residual Deviance	df	Deviance	χ2p value
Exam points only	2303	82.840
Exam points + quarter	2298	79.366	5	3.473	0.6274
Exam points × quarter	2293	78.475	5	0.892	0.9708

^aValues have 95% confidence intervals that overlap.

^bValues have 95% confidence intervals that overlap.

Student Equivalence across Quarters

Across all six quarters of the study, there was a strong relationship between the Predicted Grade and actual grade for each student. In regression analyses, Predicted Grade explained between 51 and 64% of the variation in final grade; slopes ranged from 0.88 to 1.13 (complete data not shown). Furthermore, analysis of deviance indicates no significant differences among the regressions of Predicted Grade on actual grade across quarters (Table 5). These data support the earlier claim by Freeman et al. (2007) that the Predicted Grade model is a robust index of student ability and preparedness across quarters and years.

Table 5.

Robustness of the Predicted Grade model ANCOVA fit by GLMs incorporating the effect of predicted grade, quarter, and the interaction term predicted grade by quarter; the response variable is actual grade (GLM with binomial error distribution). Analysis of deviance shows that slope and intercept do not significantly vary across quarter

Model	Residual df	Residual deviance	df	Deviance	χ2p value
Predicted grade only	2276	306.616
Predicted grade + quarter	2271	298.432	5	8.184	0.1464
Predicted grade × quarter	2266	297.386	5	1.047	0.9587

An ANOVA indicates significant heterogeneity in Predicted Grades across quarters (Table 6; F = 13.2, df = 5, 2351, p ≪ 0.001). Post-hoc Tukey's Honestly Significant Difference tests demonstrate that this heterogeneity was distributed across quarters in the study: Of the 15 pairwise tests, only six were not significantly different, and these crossed levels of course structure (data not shown).

Table 6.

Average predicted grades across quarters

	Spring 2002	Spring 2003	Spring 2005	Autumn 2005	Autumn 2007	Autumn 2009
Mean ± SD	2.46 ± 0.72	2.57 ± 0.73	2.64 ± 0.70	2.67 ± 0.60	2.85 ± 0.66	2.70 ± 0.61
n	327	338	334	328	339	691

Evaluating the Drop Rate

Among five quarters from Spring 2002 through Autumn 2007, drop rates varied from 1.8 to 3.6%. A χ² analysis indicates no heterogeneity in drop rate as course design changed from low to medium to high structure (χ² = 3.9, df = 4; p = 0.42). Significant heterogeneity occurs when the drop rate of 6.1% in Autumn 2009 is added to the analysis, however (χ² = 21.5, df = 5; p < 0.001). This increase is probably due to 1) a change in enrollment from 350 to 700, and 2) a change in departmental policy that loosened restrictions on repeating the course.

Changes in Failure Rate in Biology 180

A χ² analysis of the number of students who took the final and received a grade, and were above and below the 1.5 threshold, confirms significant differences across quarters (Table 7; χ² = 44.7, df = 5; p ≪ 0.001).

Table 7.

Failure rates across quarters

	Low structure	Moderate structure			High structure
	Spring 2002	Spring 2003	Spring 2005	Autumn 2005	Autumn 2007	Autumn 2009
Percentage of students < 1.5	18.2	15.8	10.9	11.7	7.4	6.3
n	324	333	330	333	336	653

This result is confounded, however, by changes in student academic ability across quarters, reported earlier in the text. To control for student academic characteristics, we constructed a generalized linear mixed-model (GLMM) to test the hypothesis that level of course structure plays a significant role in explaining the proportion of students failing each quarter. Specifically, we analyzed the decline in proportion of students failing as a function of those predicted to fail in each quarter at each level of structure. As before, failure was defined as a grade insufficient to continue in the introductory series (<1.5).

Using multi-model inference (MMI), the model with the most explanatory power contained proportion failing as the response variable, with predicted failure proportion and level of course structure treated as fixed effects and quarter treated as a random effect. The criteria for model selection were 1) the lowest Akaike information criterion (AIC) with a difference in AIC (ΔAIC) greater than two, along with 2) a significant LRT (Table 8). The LRT indicates that the decline in proportion of students failing, as a function of increasing structure, was significantly greater than the decline predicted by the distribution of predicted grades (p = 0.027).

Table 8.

MMI: Models and comparison criteria. Best-fit models are recognized by 1) the conservative LRT p value of the lowest AIC model or 2) a ΔAIC > 2. Note that the LRTs are hierarchical: The p value reported on each row is from a test comparing the model in that row with the model in the row below it.

Model	df	AIC	ΔAIC	ω	logLikelihood	LRT (p value)
Structure + predicted	5	1610.27	—	0.47	−800.14	0.027
Predicted	3	1613.5	3.22	0.09	−803.75	0.098
Structure × predicted	7	1613.68	3.4	0.43	−799.84	2.2e-16
Structure	4	1903.27	293	0	−947.64	0.0015
Null	2	1912.3	302.02	0.01	−954.15

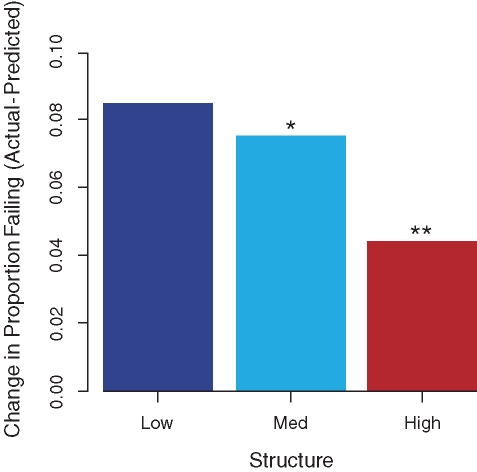
Moderate levels of course structure had a marginal effect on failure rate (Figure 3; p = 0.06), whereas high levels of course structure had a statistically significant impact on reducing failure rates independent of changes in student characteristics (Figure 3; p = 0.00004).

Figure 3.

Failure rates controlled for Predicted Grade, as a function of course structure. In this study, low-, medium-, and high-structure courses rely primarily on Socratic lecturing, some active learning and formative assessment, and extensive active learning (no lecturing) and formative assessment, respectively. The difference between the proportion of students predicted to fail and the actual proportion failing decreases with increasing structure (GLMM, binomial error n = 2267, *p = 0.06, **p = 0.0004).

DISCUSSION

The negative association between the Weighted Bloom's Indices and the PES values supports the claim that questions that are higher on Bloom's taxonomy of learning are harder, and both methods of assessing exam equivalence suggest that exam difficulty increased in highly structured versions of the course (Table 3, b and c). The 2–3% drop in PES in the highly structured courses, relative to the PES values in the low- and medium-structure courses, represents 8–12 total exam points over the quarter—enough to drop students’ final grades 0.1–0.2, on average, in the highly structured courses. This difference, and the uptick in the Weighted Bloom's Index in Autumn 2009, supports the instructors’ impression—that he wrote harder exams because the reading quizzes implemented in those quarters had already presented lower-level questions.

It is important to note that the exams analyzed here appear rigorous. Although the Weighted Bloom's Index and PES will become more informative if and when values are reported for other courses, instructors, and institutions, the data indicate that an average Biology 180 exam question in this study is at the application level of Bloom's taxonomy (Table 3b).

Finally, the data reported in Table 4 support the hypothesis that the large number of “practice points” available in highly structured versions of the course did not inflate grades, and thus did not affect changes in the failure rate.

Although student academic ability and preparedness varied among quarters, it did not vary systematically with changes in course structure. The results of the GLMM, which controlled for heterogeneity in student preparedness and capability, support the conclusion reported earlier for moderately structured courses (Freeman et al., 2007), and identify an even stronger drop in failure rate as course structure increased.

Thus, the data presented here support the hypothesis that increasing course structure can help reduce failure rates in an introductory biology course—from 18.2 to 6.3% (Table 7). They are consistent with data from other STEM disciplines suggesting that intensive use of active-learning exercises can help capable but underprepared students succeed in gateway courses (e.g., Beichner et al., 2007).

It is unlikely that this pattern is due to the changes in enrollment or exam format that occurred over the course of the study. The general expectation is that student achievement is higher in smaller classes, but the lowest failure rate in this study occurred in a quarter with 700 students enrolled—more than double the next largest enrollment. We would also argue that the change in exam format that occurred that quarter, with 2-h-long exams replacing a 2-h comprehensive final, is not responsible for the dramatic drop in failure rate. The Weighted Bloom's Indices and PES values, for example, indicate that the exams in the altered format were the highest-level and the hardest in the study.

It is important to note that the failure rates reported in this course—even before implementing highly structured course designs—were much lower than failure rates for gateway courses at many other institutions and other STEM disciplines (Table 1). We propose that this pattern is due to enrollments in Biology 180 consisting primarily of sophomores who had already completed a three-quarter, introductory chemistry sequence for majors. On our campus, the initial course in the chemistry series enrolls ∼2500 students annually—approximately half of a typical freshman class. Only ∼1500 students per year take the last course in the introductory chemistry series, however. Thus, it is likely that many underprepared students who might have taken Biology 180 were ineligible, due to a failure to complete the chemistry prerequisite.

Would highly structured course designs reduce failure rates more or less if most students were freshmen—before they had been “screened” by a chemistry prerequisite? The experiment to answer this question is underway. Our department has now removed the chemistry prerequisite for Biology 180—a change that became effective in Winter 2010—and recent quarters have enrolled up to 50% first-year students. It will be interesting to test whether highly structured course designs analyzed here have an impact on this increasingly younger student population.

The Role of Reading Quizzes

If the benefit of highly structured courses is to help students gain higher-order cognitive skills, what role do reading quizzes play? By design, these exercises focus on Levels 1 and 2 of Bloom's taxonomy—where active learning may not help. We concur with the originators of reading quizzes (Crouch and Mazur, 2001): Their purpose is to free time in class for active learning exercises that challenge students to apply concepts, analyze data, propose experimental designs, or evaluate conflicting pieces of evidence.

As a result, reading quizzes solve one of the standard objections to active learning—that content coverage has to be drastically reduced. Reading quizzes shift the burden of learning the “easy stuff”—the vocabulary and basic ideas—to the student. The premise is that this information can be acquired by reading and quizzing as well as it is by listening to a lecture.

Without reading quizzes or other structured exercises that focus on acquiring information, it is not likely that informal-group, in-class activities or peer instruction with clickers will be maximally effective. This is because Bloom's taxonomy is hierarchical (Bloom et al., 1956). It is not possible to work at the application or analysis level without knowing the basic vocabulary and concepts. We see reading quizzes as an essential component of successful, highly structured course designs.

New Tools for Assessing Exam Equivalence

This study introduces two new methods for assessing the equivalence of exams across quarters or courses: the Weighted Bloom's Index based on Bloom's taxonomy of learning and the PES based on predictions of average performance made by experienced graders. These approaches add to the existing array of techniques for controlling for exam difficulty in STEM education research, including use of identical exams (Mazur, 1997; Freeman et al., 2007); concept inventories or other standardized, third-party tests (e.g., Hestenes et al., 1992); and isomorphic or “formally equivalent” questions (e.g., Smith et al., 2009).

The Weighted Bloom's Index also has the potential to quantify the degree to which various courses test students on higher-order cognitive skills. In addition to assessing Weighted Bloom's Indices for similar courses across institutions, it would be interesting to compare Weighted Bloom's Indices at different course levels at the same institution—to test the hypothesis that upper-division courses primarily assess the higher-order thinking skills required for success in graduate school, professional school, or the workplace.

The analyses reported here were designed to control for the effects of variation in the instructors, students, and assessments. More remains to be done to develop techniques for evaluating exam equivalence and student equivalence. With adequate controls in place, however, discipline-based research in STEM education has the potential to identify course designs that benefit an increasingly diverse undergraduate population. In the case reported here, failure rates were reduced by a factor of three. If further research confirms the efficacy of highly structured course designs in reducing failure rates in gateway courses, the promise of educational democracy may come a few steps closer to being fulfilled.