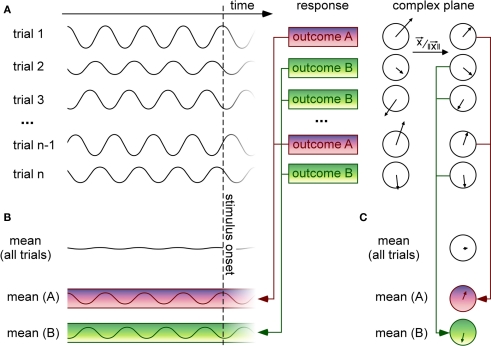
Figure 1.

Methods for linking pre-stimulus EEG phase to trial-by-trial variations of a discrete behavioral response. (A) On each trial, a time-varying signal (such as an EEG waveform) is recorded before stimulus onset. Here the signal is represented as oscillatory, but it could also correspond to a band-pass filtered version of a noisy, non-oscillatory signal. For each trial, the observer provides a behavioral response with discrete outcomes [here two possible outcomes (A,B)] corresponding, e.g., to distinct percepts (seen vs. unseen, category (A vs. B)], or to quantized reaction times (e.g., slow vs. fast), etc. On the right, the time-domain signal recorded on each trial is expressed as a vector in the complex plane (which can be calculated using Fourier or wavelet time–frequency decomposition methods). The direction of the vector and its length represent the phase and the amplitude (respectively) of the oscillatory signal recorded in a given time window of interest. (B) Since the moment of stimulus onset is unpredictable, the pre-stimulus mean over all trials is near-zero. However, if certain oscillatory phases systematically induce one or the other behavioral outcomes, then selectively averaging the signals for trials grouped according to the behavioral response should reveal oscillations with distinct phase angles. Here the magnitude of the resulting oscillation appears constant at all pre-stimulus times but in practice, due to external and measurement noise, the phase difference is more likely to be visible just before stimulus onset. This method essentially corresponds to an ERP computed before, rather than after the stimulus onset. (C) Another method consists in selectively averaging the vectors for each trial group in the complex domain; prior to averaging, each vector is normalized to a unit length, implying that its phase will always equally contribute to the average, regardless of its amplitude [without this normalizing step, the method would actually give equivalent results to the one described in (B)]. This step is important because amplitude modulations that would occur independently of phase effects would tend to obscure them. The length of the resulting vector after averaging is called “phase-locking value” (PLV) or “inter-trial coherence” (ITC; Lachaux et al., 1999). The phase locking is weak when the distribution of phase angles across trials is uniform (as should occur when all trials are pooled together regardless of behavioral outcome); if certain phase angles systematically induce one specific behavioral outcome, on the other hand, this phase locking should be significantly increased by considering only the trials with this outcome.