Abstract
Background
The aim of the study was to find a simple intravenous glucose tolerance test (IVGTT) that can be used to estimate insulin sensitivity.
Methods
In 20 healthy volunteers aged between 18 and 51 years (mean, 28) comparisons were made between kinetic parameters derived from a 12-sample, 75-min IVGTT and the Mbw (glucose uptake) obtained during a hyperinsulinemic euglycemic glucose clamp. Plasma glucose was used to calculate the volume of distribution (Vd) and the clearance (CL) of the injected glucose bolus. The plasma insulin response was quantified by the area under the curve (AUCins). Uptake of glucose during the clamp was corrected for body weight (Mbw).
Results
There was a 7-fold variation in Mbw. Algorithms based on the slope of the glucose-elimination curve (CL/Vd) in combination with AUCins obtained during the IVGTT showed statistically significant correlations with Mbw, the linearity being r2 = 0.63-0.83. The best algorithms were associated with a 25-75th prediction error ranging from -10% to +10%. Sampling could be shortened to 30-40 min without loss of linearity or precision.
Conclusion
Simple measures of glucose and insulin kinetics during an IVGTT can predict between 2/3 and 4/5 of the insulin sensitivity.
Introduction
The best established methods of measuring insulin resistance are the hyperinsulinemic euglycemic glucose clamp and the intravenous glucose tolerance test (IVGTT), of which former is the "gold standard" [1-3]. These methods have a long history as investigative tools in diabetes research but are too cumbersome to be used during surgery, although insulin resistance develops in this setting [4,5].
The aim of this project is to evaluate a simplified IVGTT test that lasts for 30, 40 or 75 min. This test is less labour-intensive than both the glucose clamp and the conventional IVGTT. Analysis of the data is based on a comparison between the "strength" of the insulin response and the elimination kinetics of glucose. A commonly used expression for the "strength" of a physiological factor is the area under the curve (AUC), which was applied here on insulin, while the slope of the elimination curve for glucose served to quantify the "effect".
The hypothesis was that the test could predict insulin resistance with the same or higher precision than the "minimal model" (MINMOD) which is typically based on a longer IVGTT and quite demanding mathematically [6,7]. We assessed this objective by comparing the simplified IVGTT with the result of the glucose clamp in 20 healthy volunteers.
Materials and methods
Twenty non-obese healthy volunteers, 8 females and 12 males, aged between 18 and 51 (mean, 28) years and with a body weight of 49-88 (mean, 68) kg, were studied. None of them had any disease requiring medication, and routine blood chemistry confirmed the absence of metabolic disease (Table 1, top). The study was approved by the Regional Ethics Committee in Stockholm and complied with the Helsinki Declaration. Each volunteer gave his/her written consent to participate.
Table 1.
Baseline data and key results for the IVGTT and the glucose clamp.
| Parameter | Mean (SD), or median (25th-75th percentiles) |
Unit |
|---|---|---|
| Health status | ||
| Body mass index | 23.4 (2.3) | kg/m2 |
| HbA1c | 44 (0.5) | mmol/mol |
| Blood Hb concentration | 126 (14) | mmol/L; |
| Serum creatinine concentration | 83 (3) | μmol/L |
| Serum sodium and potassium concentrations | 141 (2); 3.9 (0.3) | mmol/L |
| IVGTT | ||
| Plasma glucose, baseline | 4.8 (0.5) | mmol L-1 |
| Plasma insulin, baseline | 21 (12-24) | pmol L-1 |
| Volume of distribution (Vd) | 14.0 (6.5) |
L |
| per kg body weight | 0.20 (0.09) | L kg-1 |
| Clearance (CL) | 0.63 (0.26) |
L min-1 |
| per kilo body weight | 9.3 (3.8) | ml min-1 kg-1 |
| Insulin sensitivity (SI) of MINMOD | 16 (7-32) | 10-5 L pmol-1 min-1 |
| Glucose effectiveness (SG) in MINMOD | 13 (5-26) | 10-3 min-1 |
| Glucose clamp | ||
| Plasma glucose, baseline | 5.0 (1.0) | mmol L-1 |
| Plasma insulin, baseline | 16 (7-30) | pmol L-1 |
| Plasma glucose, mean 90-120 min | 5.7 (0.3) | mmol L-1 |
| Plasma insulin, mean 90-120 min | 167 (34) | pmol L-1 |
| Glucose metabolism, M, 90-120 min | 3.1 (1.2) | mmol min-1 |
| Mbw = per kg body weight | 45 (15) | μmol min-1 kg-1 |
IVGTT = intravenous glucose tolerance test
Euglycemic hyperinsulinemic clamp
The subjects reported at the laboratory between 7.30-8.00 AM. A superficial dorsal hand vein was cannulated in retrograde direction with a small three-way needle and kept patent by repeated flushing with saline solution. The hand and lower arm were warmed by a heating pad for intermittent sampling of arterialized venous blood for glucose determination (Hemocue, Ängelholm, Sweden). In the opposite arm an intravenous catheter was inserted into the left antecubital vein for insulin and glucose infusion.
During the 120-min test, insulin 20 mU · BSA m-2 · min-1 (Human Actrapid, NovoNordisk A/S, Bagsverd, Denmark) was infused along with 20% dextrose (Fresenius Kabi, Uppsala, Sweden). Baseline blood samples were drawn and the euglycemic hyperinsulinemic clamp was initiated by infusion of a bolus dose of insulin for 4 minutes followed by a step-wise increase in glucose for 10 min. The glucose infusion rate was adjusted to keep the subjects' blood glucose level constant at 5 mmol/L on the basis of arterialized samples withdrawn every 5 min from the dorsal hand vein catheter [8]. The infusion rate during the last 30 min, after correction for body weight, was taken to represent the metabolism of glucose (Mbw) [1-3].
Intravenous glucose tolerance test
On the second occasion, 1-2 days apart from the clamp study and after 12 h of fasting, a regular intravenous glucose tolerance test (IVGTT) was performed to determine the early insulin response phase (0-10 min), as well as the area-under-the-curve for insulin (AUCins being total insulin and ΔAUCins above baseline) and C-peptide for up to 75 minutes. A bolus of glucose (300 mg/kg in a 30% solution) was given within 60 sec into the antecubital vein. Blood was sampled from the contralateral antecubital vein at 0, 2, 4, 6, 8, 10, 20, 30, 40, 50, 60 and 75 min for assessment of the plasma glucose, insulin, and C-peptide concentrations. Plasma glucose was measured by the glucose oxidase method used by the hospital's routine laboratory. Plasma insulin and C-peptide were measured using ELISA kits (Mercodia AB, Uppsala, Sweden).
Calculations
The pharmacokinetics of the glucose load was analysed using a one-compartment open model [9]. Here, the plasma concentration (G) at any time (t) resulting from infusing glucose at the rate Ro is calculated from the following differential equation:
where Gb is the baseline glucose, Vd is the volume of distribution, CL the clearance and CL/Vd the slope of the glucose elimination curve. The half-life (T1/2) of the exogenous glucose load was obtained as (ln 2 Vd /CL). The AUC for plasma insulin was calculated by using the linear trapezoid method.
The glucose and insulin data were also analyzed by applying the "minimal model" (MINMOD) of Bergman et al. [6,7]. The kinetic system consists of two differential equations:
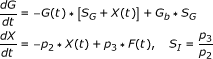 |
where SI = glucose sensitivity, SG = glucose effectiveness, X(t) is insulin action in the interstitial fluid space, and F(t) a function for the elevation of plasma insulin above the basal level. p2 is the removal rate of insulin from the interstitial fluid space while p3 describes the movement of circulating insulin to the interstitial space.
The best estimates for the unknown parameters in these models were estimated for each of the 20 experiments individually by nonlinear least-squares regression. No weights were used. The mathematical software was Matlab R2010a (MathWorks, Natick, MA, USA).
The insulin sensitivity was also quantified by "Quicki", which is the inverse of the logarithm of the product of plasma glucose and plasma insulin at baseline [10]. Finally, we tested the recently proposed equation by Tura et al. [11] for short IVGTTs:
where CS1 a surrogate measure for insulin sensitivity, KG is the slope of the glucose elimination curve (same as CL/Vd) and T is the time after 10 min.
Statistics
The results were presented as mean and standard deviation (SD) and, when there was a skewed distribution, as the median (25th-75th percentile range). Simple or multiple linear regression analysis, in which r2 is the coefficient of determination, was used to express "linearity" when studying the relationship between the Mbw of the glucose clamp (control) and various algorithms for insulin sensitivity derived from data collected during the IVGTT. The error in the prediction of Mbw associated with each regression analysis was obtained as [100% (fitted-measured)/measured]. The change in prediction error obtained by restricting the analysis period from 75 to 40 and 30 min was tested by Friedman's test. All reported correlations were statistically significant by P < 0.05.
Results
Clamp
Mbw of the glucose clamp varied 7-fold (Table 1, middle). Between 2/3 and 4/5 of this variability could be predicted by linear regression based on indices of glucose and insulin turnover obtained from the data collected during the IVGTT.
IVGTT
All 20 experiments could be analysed with the proposed equations for plasma glucose and insulin kinetics (Figure 1; Table 1, bottom). However, the glucose kinetics of 3 experiments were studied only up to 40 min due to rapid elimination followed by mild hypoglycemia, which otherwise distorted the elimination slope.
Figure 1.
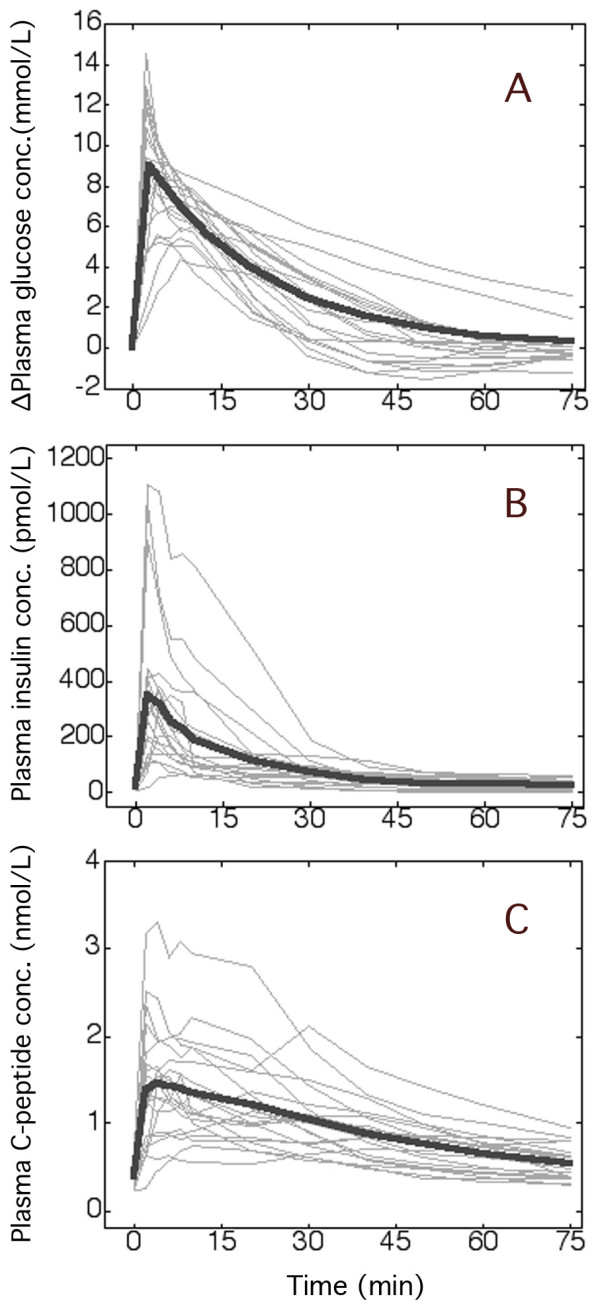
Plasma concentrations during the IVGTT. Plasma glucose above baseline (A) and the plasma insulin (B) and C-peptide concentrations (C) during 20 intravenous glucose tolerance tests (IVGTTs). The thin lines represent one experiment. The thick line in A is the modelled average curve, based on the kinetic data shown in Table 1, while B and C are the mean for each point in time.
First key algorithm
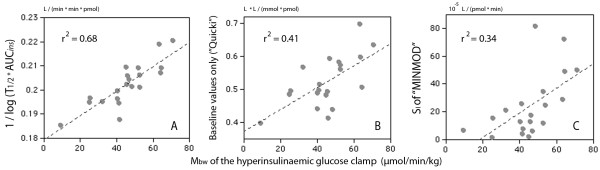
One useful algorithm contained the 10log of the product of T1/2 for the exogenous glucose load and AUC for plasma insulin. Various modifications of the algorithm correlated with Mbw with a linearity of r2 = 0.63-0.68 (Figure 2A, Table 2).
Figure 2.
Insulin resistance as given by the glucose clamp and a short IVGTT. (A) The relationship between Mbw of the hyperinsulinemic euglycemic clamp and a surrogate expression for insulin sensitivity based on the half-life of glucose and the area under the curve (AUC) for plasma insulin during a 75-min IVGTT in 20 volunteers. (B) Same equation but using only baseline plasma glucose and insulin concentrations. (C) Mbw versus insulin sensitivity obtained by "minimal model" (MINMOD) analysis.
Table 2.
Linear correlations between the IVGTT and the glucose clamp.
| Y | X | Equation | Time period |
r2 | 25th-75th percentiles of prediction error | |
|---|---|---|---|---|---|---|
| Mbw | 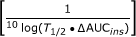 |
Y = -172 + 1040 X | 75 min | 0.63 | -10% | +16% |
| Y = -201 + 1179 X | 40 min | 0.63 | -8% | +20% | ||
| Y = -219 + 1256 X | 30 min | 0.62 | -12% | +26% | ||
| Same equation, but using total insulin AUC | Y = -220 + 1310 X | 75 min | 0.68 | -11% | +9% | |
| Y = -218 + 1287 X | 40 min | 0.63 | -8% | +12% | ||
| Y = -248 + 1419 X | 30 min | 0.66 | -8% | +20% | ||
| Mbw | 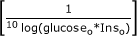 |
Y = -19 +124 X | Baseline "Quicki" |
0.41 | -14% | +11% |
| Mbw | SI of MINMOD 10-5 | Y = 36 + 0.38 X | 75 min | 0.34 | -16% | +24% |
Equations compare the cellular uptake of glucose obtained by the glucose clamp (Mbw,; μmol min-1 kg-1) and indices of glucose kinetics and plasma insulin obtained during an intravenous glucose tolerance test (IVGTT) in 20 non-obese volunteers.
T1/2 = half-life of exogenous glucose (units: min)
Glucoseo, Inso = plasma concentrations of glucose and insulin at baseline (units: mmol L-1 and pmol L-1)
AUCins = area under the curve for plasma insulin over time (unit: pmol min L-1)
MINMOD = "minimal model analysis" according to Bergman et al. [6]
Consistently weaker correlations were obtained on correcting Mbw for the steady state plasma glucose and insulin concentrations (data not shown, r2≈0.40-0.50).
This key algorithm has the same construction as "Quicki" which uses only the baseline values of plasma glucose and insulin. The original "Quicki" equation correlated with Mbw with a linearity of only r2 = 0.41 (Figure 2B) which was still slightly stronger than for other similar expressions, such as HOMA-IR (r2 = 0.35) and the G/I ratio (r2 = 0.39) [2].
MINMOD and Tura's equation
Weaker correlations were also obtained when comparing Mbw with the insulin sensitivity as obtained by "minimal model analysis" (MINMOD) of the IVGTT data (r2 = 0.34, Figure 2C). Plots of X(t) obtained by MINMOD indicated that the insulin concentration at the effect site was highest at 18 min (13-33) min.
The recently published equation by Tura et al. [11] correlated with Mbw with a linearity of r2 = 0.54 for the period 0-40 min. Logarithm-transformation of Tura's surrogate measure for insulin sensitivity increased r2 to 0.65.
Second key algorithm
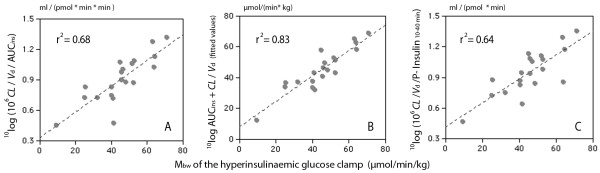
Another equation applied the parameters of the glucose kinetics directly and might therefore be easier to handle (Table 3, Figure 3A).
Table 3.
Further linear correlations between the IVGTT and the glucose clamp.
| Y | X | Equation | Time period |
r2 | 25th-75th percentiles of prediction error | |
|---|---|---|---|---|---|---|
| Mbw | 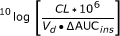 |
Y = -2.5 + 45.4 X | 75 min | 0.64 | -10% | +16% |
| Y = -8.6 + 51.5 X | 40 min | 0.64 | -8% | +21% | ||
| Y = -13.8 + 54.9 X | 30 min | 0.64 | -12% | +25% | ||
| Same equation, but using total insulin AUC | Y = -2.8 + 53.4 X | 75 min | 0.68 | -10% | +9% | |
| Y = -6.1 + 54.0 X | 40 min | 0.64 | -8% | +13% | ||
| Y = -14.5 + 60.0 X | 30 min | 0.67 | -8% | +20% | ||
| Mbw | 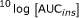 |
Y = 206 - 49.0 X + 340 CL/Vd | 75 min | 0.70 | -11% | +16% |
| Y = 224 - 56.4 X + 480 CL/Vd | 40 min | 0.74 | -10% | +20% | ||
| Y = 223 - 57.9 X + 580 CL/Vd | 30 min | 0.70 | -10% | +23% | ||
| Same equation, but using total insulin AUC | Y = 265 - 63.6 X + 383 CL/Vd | 75 min | 0.83 | -9% | +11% | |
| Y = 262 - 65.4 X + 488 CL/Vd | 40 min | 0.82 | -10% | +11% | ||
| Y = 260 - 67.1 X + 602 CL/Vd | 30 min | 0.79 | -8% | +14% | ||
| Mbw | 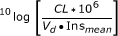 |
Y = -99 + 54.0 X | 75 min | 0.63 | -10% | +16% |
| Y = -9 + 51.5 X | 10-40 min | 0.64 | -8% | +21% | ||
| Y = -14 + 54.9 X | 10-30 min | 0.64 | -12% | +26% | ||
Vd, CL = volume of distribution and clearance of glucose for the IVGTT (units: L and L min-1, respectively).
Insmean, = mean value plasma of insulin (units: pmol L-1)
AUCins = area under the curve for plasma insulin over time (unit: pmol min L-1)
Figure 3.
Insulin resistance by the glucose clamp and a short IVGTT. The relationship between Mbw and various combinations of the clearance (CL) and volume of distribution (Vd) of glucose and (A, B) the area under the curve for plasma insulin (AUCins) during the 75-min IVGTT, or (C) using the mean plasma insulin level measured at 10, 20, 30, and 40 min.
A promising modification of this second key algorithm inserted the parameters of the glucose kinetics and the AUC for plasma insulin in a multiple regression equation, which yielded a maximum linearity of r2 = 0.83 for the relationship between the IVGTT and Mbw (Table 3, Figure 3B).
Slight strengthening of the linearity was always obtained by using AUCins without correction for the baseline plasma insulin level (Tables 2 and 3).
Exploratory analyses
Replacing AUCins by the sum of the plasma insulin concentrations for various periods of time did not greatly impair linearity or the prediction error (Table 3, Figure 3C).
The overall linear correlation between the AUC for C-peptide and insulin was r2 = 0.66. However, replacing AUCins by AUC for C-peptide in the equations proposed above greatly reduce their linearity with Mbw (r2 ≈ 0.20).
Discussion
IVGTT versus the glucose clamp
The present study searched for an approach to estimate insulin sensitivity that requires only minimum of resources. The results are presented as a number of regression equations that compare Mbw of the glucose clamp (control) with minor mathematical variations of two key algorithms based on data derived from a short IVGTT. Any of them may be used as substitutes for a glucose clamp in healthy volunteers, although some offer stronger linearity and a smaller prediction error than others.
The first of the key algorithms, shown on top of Table 2, is constructed in a way similar to the "Quicki" [10]. However, the linearity was much stronger when based on the IVGTT as compared to the baseline data used in the "Quicki" (Figure 2A, B).
Various modifications of the second key algorithm, presented in Table 3, were also tested. A promising change was to consider the sum of the slope of the glucose elimination curve, CL/Vd, and the insulin "pressure", AUCins, in a multiple regression equation. This approach could explain up to 83% of the inter-individual variability in Mbw (Figure 3).
Reducing the sampling time from 75 min to 40 min, or even 30 min, had only small undue effects on our quality measures, i.e. the linearity and the prediction error.
Corrections for baseline concentrations
The relationship between plasma insulin and glucose is not a simple one. The dose-response curve is hyperbolic (saturation kinetics) [2,3] and the CL of glucose is related to the 10log of the insulin level [3,12].
The saturation kinetics makes it questionable to correct Mbw for the steady state insulin level in plasma to yield the Mbw/I ratio, although this is often done. The high concentration of insulin at the effect site at the end of a glucose clamp probably changes CL very little for a large increment in plasma insulin. Correcting Mbw for steady state plasma insulin also resulted in poorer correlations vis-à-vis the IVGTT.
Likewise, one may question whether baseline insulin should be subtracted from AUCins when estimating Mbw from an IVGTT test. Although being a logical and commonly used correction, disregarding the baseline strengthened the correlations in the present study. Inhibition of the endogenous glucose production taking place early during the IVGTT is likely to make the insulin concentration below baseline govern the disposition of both the exogenous and the endogenous glucose later during the test. Differences in the mathematical correlations between the glucose clamp and the IVGTT were fairly small, however, and we therefore conclude that correcting for baseline insulin can be done, but is not essential.
Comparison with other methods
The precision by which our 12-sample IVGTT could predict insulin sensitivity stands out favourably in comparison with other and more complex approaches, as presented in a review by Borai et al. [1].
A previous study of MINMOD based on a series of 25 blood samples showed a linearity to the glucose clamp that was quite similar to the r2 = 0.34 found here [13]. The new algorithms thus offered far better linearity than MINMOD in the present setting. MINMOD contains four unknown parameters that become gradually more difficult to estimate with good precision the fewer samples there are available. Moreover, MINMOD is not well suited for short sampling times. In contrast, the new algorithms included least-square regression estimation of only two parameters, CL and Vd, which makes them less sensitive for a reduction of sampling time and/or sampling intensity. With 12 samples, CL and Vd were estimated with the standard errors that averaged less than 10% (data not shown).
Tura et al. [11] recently compared the ratio of the glucose disappearance rate and AUCins with SI and Mbw in a retrospective analysis of studies comprising both volunteers and diabetic and postoperative patients who had undergone a frequently sampled 50-min IVGTT and a conventional 2-hour glucose clamp. Good correlations between these indices of insulin sensitivity were claimed for all subgroups. The basic equation used is quite similar to the one we propose on the top of Table 3. However, they did not use the 10log of AUCins and corrected this area for the group average SI value. They also divided the expression by the sampling time, which we find questionable since plasma insulin but not KG decreases with time. This fact must be handled by using a unique equation for each sampling time, as in Tables 2 and 3.
Limitations during surgery
The present study suggests two key algorithms, together with various modifications thereof, that may be used to estimate insulin sensitivity based on data derived from a short IVGTT performed in healthy volunteers. In a subsequent study, these algorithms will be validated in the pre- and postoperative settings. Our interest in this topic stems from a wish to study insulin resistance during surgery. Virtually all non-diabetic patients develop transient type 2 diabetes as a part of the stress response to surgery [4,5]. Too little research has been performed to investigate the reasons and consequences of this insulin resistance, which is probably due to the demanding and complex nature of both the glucose clamp and the IVGTT. In this setting, it is important that the blood sampling and the time and resources required for the test are kept low. Moreover, the test should impose only a slight burden on the body's physiology.
Conclusion
The ratio of the slope of the glucose elimination curve and the AUC for plasma insulin during a short IVGTT showed a strong linear correlation (r2 = 0.63-0.83) with the insulin sensitivity as obtained by the glucose clamp technique in healthy volunteers.
Abbreviations
AUC: area under the curve; CL: clearance; IVGTT: intravenous glucose tolerance test; MINMOD: minimal model analysis; Vd: volume of distribution; T1/2: half-life.
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
RH provided the study idea, made the calculations, and wrote the manuscript. SL and FL assisted during the experiments. TN wrote the ethics application and arranged for the experiments.
Contributor Information
Robert G Hahn, Email: r.hahn@telia.com.
Stefan Ljunggren, Email: stefan.ljunggren@sodertaljesjukhus.se.
Filip Larsen, Email: filip.larsen@ki.se.
Thomas Nyström, Email: thomas.nystrom@sodersjukhuset.se.
Acknowledgements and Funding
Tobias Gebäck, Chalmers School of Technology, Gothenburg, Sweden, programmed the MINMOD in the Matlab environment. Financial support was received from the Stockholm County Council (Grant number 2009-0433), Olle Engkvist Byggmästare Foundation, Karolinska institute, Swedish Society for Medical Research, and the Swedish Society of Medicine. The work was performed at The Metabolic Laboratory of the Endocrinology Department at Södersjukhuset, Stockholm, Sweden.
References
- Borai A, Livingstone C, Ferns GAA. The biochemical assessment of insulin resistance. Ann Clin Biochem. 2007;44:324–342. doi: 10.1258/000456307780945778. [DOI] [PubMed] [Google Scholar]
- Muniyappa R, Lee S, Chen H, Quon MJ. Current approaches for assessing insulin sensitivity and resistance in vivo: advantages, limitations, and appropriate usage. Am J Physiol Endocrinol Metab. 2008;294:E15–26. doi: 10.1152/ajpendo.00645.2007. [DOI] [PubMed] [Google Scholar]
- Ferrannini E, Mari A. How to measure insulin sensitivity. J Hypertens. 1998;16:895–906. doi: 10.1097/00004872-199816070-00001. [DOI] [PubMed] [Google Scholar]
- Brandi LS, Frediani M, Oleggini M, Mosca F, Cerri M, Boni C, Pecori N, Buzzigoli G, Ferrannini E. Insulin resistance after surgery: normalization by insulin treatment. Clin Sci. 1990;79:443–450. doi: 10.1042/cs0790443. [DOI] [PubMed] [Google Scholar]
- Ljungqvist O, Thorell A, Gutniak M, Häggmark T, Efendic S. Glucose infusion instead of preoperative fasting reduces postoperative insulin resistance. J Am Coll Surg. 1994;178:329–336. [PubMed] [Google Scholar]
- Bergman RN, Ider YZ, Bowden CR, Cobelli C. Quantitative estimation of insulin sensitivity. Am J Physiol. 1979;236:667–677. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
- Nittala A, Ghosh S, Stefanovski D, Bergman R, Wang X. Dimensional analysis if MINMOD leads to definition of the disposition index of glucose regulation and improved simulation algorithm. Biomed Engineering OnLine. 2006;5:44–57. doi: 10.1186/1475-925X-5-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deFronzo RA, Tobin JD, Andres R. Glucose clamp technique: a method for quantifying insulin secretion and resistance. Am J Physiol. 1979;273:E214–23. doi: 10.1152/ajpendo.1979.237.3.E214. [DOI] [PubMed] [Google Scholar]
- Sjöstrand F, Hahn RG. Validation of volume kinetic analysis of glucose 2.5% solution given by intravenous infusion. Br J Anaesth. 2003;90:600–607. doi: 10.1093/bja/aeg102. [DOI] [PubMed] [Google Scholar]
- Katz A, Nambi SS, Mather K, Baron AD, Sullivan G, Quon MJ. Quantitative insulin sensitivity check index: a simple, accurate method for assessing insulin sensitivity in humans. J Endocrinol Metab. 2000;85:2402–2410. doi: 10.1210/jc.85.7.2402. [DOI] [PubMed] [Google Scholar]
- Tura A, Sbrignadello S, Succurro E, Groop L, Sesti G, Pacini G. An empirical index of insulin sensitivity from short IVGTT: validation against the minimal model and glucose clamp indices in patients with different clinical characteristics. Diabetologia. 2010;53:144–152. doi: 10.1007/s00125-009-1547-9. [DOI] [PubMed] [Google Scholar]
- Berndtson D, Olsson J, Hahn RG. Hypovolaemia after glucose-insulin infusions in volunteers. Clin Sci. 2008;115:371–378. doi: 10.1042/CS20080032. [DOI] [PubMed] [Google Scholar]
- Beard JC, Bergman RN, Ward WK, Porte D. The insulin sensitivity index in non-diabetic man: correlation between clamp-derived and IVGTT-derived values. Diabetes. 1986;35:362–369. doi: 10.2337/diabetes.35.3.362. [DOI] [PubMed] [Google Scholar]