Abstract
We present and evaluate a rigid-body, deterministic, molecular docking method, called ELMDOCK, that relies solely on the three-dimensional structure of the individual components and the overall rotational diffusion tensor of the complex, obtained from nuclear spin-relaxation measurements. We also introduce a docking method, called ELMPATIDOCK, derived from ELMDOCK and based on the new concept of combining the shape-related restraints from rotational diffusion with those from residual dipolar couplings, along with ambiguous contact/interface-related restraints obtained from chemical shift perturbations. ELMDOCK and ELMPATIDOCK use two novel approximations of the molecular rotational diffusion tensor that allow computationally efficient docking. We show that these approximations are accurate enough to properly dock the two components of a complex without the need to recompute the diffusion tensor at each iteration step. We analyze the accuracy, robustness, and efficiency of these methods using synthetic relaxation data for a large variety of protein-protein complexes. We also test our method on three protein systems for which the structure of the complex and experimental relaxation data are available, and analyze the effect of flexible unstructured tails on the outcome of docking. Additionally, we describe a method for integrating the new approximation methods into the existing docking approaches that use the rotational diffusion tensor as a restraint. The results show that the proposed docking method is robust against experimental errors in the relaxation data or structural rearrangements upon complex formation and is computationally more efficient than current methods. The developed approximations are accurate enough to be used in structure refinement protocols.
Keywords: rigid-body docking, protein complexes, residual dipolar couplings, diffusion-guided molecular assembly, ellipsoid model, ELM, PATI
Introduction
Understanding the molecular mechanisms underlying biological function requires knowledge of the three-dimensional structure of biomacromolecules and their complexes at atomic level resolution. Nuclear Magnetic Resonance (NMR) spectroscopy is currently the main method for structure characterization of proteins and nucleic acids in solution. While NMR has been fairly effective at determining structures of single-domain proteins, accurate structure determination of macro-molecular complexes and multi-domain systems remains a major challenge. One of the main difficulties here is the paucity of intermolecular Nuclear Overhauser Effect (NOE) contacts, which are scarce and difficult to detect and could be affected by interdomain motions. In lieu of NOE contact information, chemical shift perturbation (CSP) mapping can provide approximate inter-domain restraints. However, such restraints are highly ambiguous because CSPs do not identify specific pairwise contacts and should be used with caution, as perturbations in the local electronic environment of a nucleus could be caused by local conformational changes and not necessarily by direct interaction of a given atom/residue with the binding partner.
A powerful way of introducing additional structural restraints has been the use of residual dipolar couplings (RDCs), resulting from partial molecular alignment in a magnetic field,1,2 because they contain valuable structural information in terms of global, long-range orientational restraints (reviewed in3). RDCs have been used to orient molecules and bonds relative to each other either directly, using rigid-body rotation,4–8 or by incorporating RDCs as orientational restraints into protein docking9–11 (see e.g., the reviews12,13). Recently we have developed a docking method that uses RDC’s sensitivity to molecular shape to not only orient, but also position individual components (domains) in the complex relative to each other.14,15 However, in its current form, this method relies on steric alignment, and therefore requires a specific medium (e.g. bicelles, PEG/hexanol) to be added to solution and is inevitably limited by what kind of medium can be used.
Another physical characteristic sensitive to molecular shape (hence a source of long distance structural restraints) is the rotational diffusion tensor,16–18 which can be derived from NMR relaxation data.18–22 Using almost identical concepts and ideas, the diffusion tensor can be used in a way similar to RDCs to create both orientational and translational restraints for molecular docking.23 Using the diffusion tensor instead of RDCs is advantageous in that this does not require any alignment medium, and therefore can be applied to a larger variety of complexes in their native millieu. In fact, the diffusion tensor has been used as a long-range orientational restraint for structure characterization of multidomain systems.8,18,21,24 More recently the idea of using the diffusion tensor as a translational restraint in rigid docking of multi-domain proteins was introduced in Ryabov and Fushman23 and further explored in Ryabov et al.25,26 However, no docking method has yet combined the shape-related restraints derived from RDCs with the shape-related restraints from the rotational diffusion tensor.
In this paper we introduce ELMDOCK, a fast rigid-body docking method that uses the rotational diffusion tensor’s sensitivity to the overall shape of a molecule as a long-range experimental restraint. ELMDOCK is named for the ELlipsoidal Model that it uses to approximate the shape of a molecule. Similarly to,23,25 ELMDOCK uses the difference between the experimental and the predicted diffusion tensors to find the proper positioning of the second domain of the complex relative to the first one, however it uses a deterministic docking algorithm that finds the solution orders of magnitude faster than the previously described methods. In order to achieve high computational efficiency we avoid recomputation of the molecular surface, the computationally expensive part of our diffusion tensor prediction method, by developing two levels of approximations of the diffusion tensor. The first, more computationally expensive approximation, allows quick adjustment of the molecular surface under domain collision. The second approximation is a derived quadratic formula with explicit derivatives, that can quickly be evaluated under arbitrary translations of the domains without the need to fully recompute the molecular surface, and allows a fast approximation of the Jacobian, critical to Newton-like minimization algorithms. These approximation methods can therefore be integrated into more complex docking algorithms to improve their performance. For example, they can significantly speed up steps 1–3 of the docking protocol described in Ryabov et al.,26 and can also speed up the recomputation of the diffusion tensor during simulated annealing of more complicated energy functions such as proposed in.25,26 We also combine ELMDOCK with our RDC-based docking method, PATIDOCK+,15 to create the first method (ELMPATIDOCK) for docking that combines shape-related restraints from both residual dipolar couplings and spin-relaxation measurements (as well as CSP-generated restraints).
We show that, given an accurate ab initio predictor of the diffusion tensor from protein structure, it is possible to quickly and deterministically assemble a protein-protein complex by using fast approximations of the diffusion tensor. The proposed docking method, ELMDOCK, is robust against experimental errors in the NMR relaxation data and is computationally more efficient than current methods. We analyze the accuracy and efficiency of this method using synthetic data for a large variety of protein-protein complexes as well as actual experimental data for three protein systems for which the structure of the complex and diffusion data is available. We analyze the effect of flexible unstructured tails on the outcome of docking for a complex of ubiquitin and a ubiquitin-associated domain. Finally, we demonstrate that ELMPATIDOCK can improve upon the solutions of ELMDOCK by adding additional constraints.
Docking Method
We now present the detailed algorithm for ELMDOCK, our docking method for determining relative domain position in a molecule made up of two domains for which the individual three-dimensional structures and the associated relaxation data are known.
ELMDOCK requires three components. The first component is a method for determining the experimental diffusion tensor from the NMR relaxation data. We use a modified version of a computer program ROTDIF22 for extracting the experimental diffusion tensor from NMR relaxation data which allows computation of the diffusion tensor using robust as well as normal regression.
The second required component for ELMDOCK is a method for predicting the diffusion tensor given a three-dimensional structure of a molecule. The two known methods are HYDRONMR27,28 and ELM.29 Similar to previous approaches,23,25,26 we use ELM in ELMDOCK.
The final required component for ELMDOCK is a method that efficiently finds the optimal positioning of the second domain relative to the first one based on the difference between the experimental diffusion tensor (computed using ROTDIF) and the predicted diffusion tensor (computed using ELM). This new component is described in this manuscript.
Let M be a molecule made up of two domains, A and B, with experimentally measured ratio of transverse and longitudinal 15N relaxation rates ρexp,18 and the associated experimental diffusion tensors DA and DB (computed for the fully anisotropic rotational diffusion model using ROTDIF). We assume that A and B tumble together in solution and hence are characterized by a common diffusion tensor, i.e. DA and DB represent the same diffusion tensor. Our goal is to first properly orient the two domains by finding the optimal rotation matrix R*, that will orient B relative to A, and then to find the optimal translation vector x* that minimizes the difference between the predicted diffusion tensor and the “global” experimental rotational diffusion tensor, Dexp, extracted from ρexp of both domains using the newly aligned domain orientations.
Orienting Domains using Relaxation Data
First we orient domains A and B based on the rotational diffusion tensors of the complex reported by the individual domains. Here we assume that each of the tensors DA and DB has unique principal components (i.e. is fully anisotropic) and, because A and B tumble together in solution, these principal components are similar between the two tensors. To solve for R* we align A and B relative to each other using experimental relaxation data, as described in.8,18,24 We first compute the experimental rotational diffusion tensors, D̃A and D̃B, of A and B, respectively, using ROTDIF. The rotational diffusion tensors have eigendecompositions and , where RA, RB are rotation matrices (orthogonal matrices with determinant of 1) and LA, LB are the diagonal matrices of principal components of the corresponding rotational diffusion tensors. Therefore, R* can be derived by solving the equation R*RA = RB:
| (1) |
Note that due to orientational degeneracy of the diffusion tensor there is a four-fold ambiguity in the relative alignment of domains, hence four possible solutions for R*.8 One can find these possible solutions by computing an eigendecomposition of D̃2, determining the four assignments of signs to the columns of RB that make det(RB) = 1, and using Eq.(1) for each one. Also note that in the case when two or more eigenvalues of the alignment tensor are close to each other (e.g. very low rhombicity) it might not be possible to accurately orient the two domains. In this case additional experimental information, e.g. in the form of interdomain contacts, could help in identifying the correct orientation.
Overview of ELMDOCK
Let B + x represent a shift in the position of each atom of B by a vector x ∈ ℝ3. We define M(x) to be the combined structure of A and B + x.
The goal of ELMDOCK, after the domains have been properly oriented, is to find a shift x* in the position of the B molecule such that the combined molecule M(x*) has the same diffusion tensor as the experimental diffusion tensor Dexp. Specifically, we find x* such that
| (2) |
| (3) |
where F(M) is a function that predicts the diffusion tensor of a molecule M. For example F(M) could be HYDRONMR28 or ELM.29
Solving Eq.(2) directly will be slow for two reasons: First, the diffusion tensor needs to be recalculated for each iteration of the minimization. Since computing the diffusion tensor involves computation of the Richards’ smooth molecular surface, this computation is expensive. Second, a nonlinear least-squares method will be slow because of the need to approximate the Jacobian for F(M) using finite differences. The finite difference approximation leads to further problems since we expect the function to not be perfectly smooth due to the sudden changes in the surface points as the two domains collide. In addition, finite differences will require us to compute M(x) three additional times for each minimization iteration.
To explain how we solve Eq.(2) in a more efficient way we dissect the ELM method into its major components. The steps for computing the predicted diffusion tensor using ELM for any molecule M(x), described in Ryabov et al.,29 are
| (4) |
where S is the set of sample points from Richards’ smooth surface (also known as the solvent accessible surface) for molecule M(x) (computed using the program SURF30,31), C is the covariance matrix of S, and ℰ is the associated principal component analysis ellipsoid (PCAE). See Supplementary Information and reference29 for how to compute PCAE from S and how to compute the diffusion tensor of an ellipsoid using Perrin’s equations.32,33
The goal of our docking algorithm is to reverse these steps in an efficient manner so that given Dexp, we find the best fitting molecule M(x*), and hence x*. We accomplish this in two separate steps:
| (5) |
If our problem is well conditioned, small errors in the prediction of the diffusion tensor or Dexp will result in a small difference between the true solution and x*.
In step 1 we find C* by solving the equation
| (6) |
where
| (7) |
and L(C) is the function that returns the diffusion tensor of a covariance matrix C.
In step 2 we efficiently find x* by solving the equation
| (8) |
where
| (9) |
and G(x) is a function that returns the covariance matrix of the surface of a molecule M(x). In order to describe the minimization method for , we first present two methods for approximating G(x). We then use these approximation methods to efficiently minimize .
We summarize our complete docking method in Algorithm 1. The relevant references are presented in the comment section of each line, and are explained in detail in the rest of the manuscript and Supplementary Information.
Algorithm 1.
Overview of Docking Algorithm ELMDOCK
| Input: Three-dimensional structure of domain A and B, ρexp – experimental relaxation-rates ratios, G(x) – a function that computes the covariance matrix of M(x). |
| Output: x* – the translation of B that yields the best docking solution as measured by our energy function. |
| 1: Orient the A and B domains using ρexp {See above} |
| 2: Compute Dexp using ρexp from both of the domains using ROTDIF |
| 3: Step 1: Compute the covariance matrix C* from Dexp |
| 4: Step 2: Find x* by solving |
| 5: return x* |
Step 1: From Diffusion Tensor to Covariance Matrix
In this section and in the Supplementary Information we describe step 1 of our docking method, where we solve Eq.(6) by finding a covariance matrix C* of an ellipsoid that has the diffusion tensor value Dexp. Then, given the covariance matrix it is much easier to find x* since the covariance matrix is directly related to the position of the surface points of the domain, while the relationship between x* and the diffusion tensor is much harder to quantify.
Note that in ELM the orientation of the diffusion tensor Dexp and of the associated covariance matrix C* is the same. That means that the eigendecompositions of Dexp and C* are
| (10) |
and
| (11) |
By performing an eigendecomposition of Dexp, we get the values for V, Dx, Dy, and Dz. Given Dx, Dy, and Dz, we solve Perrin’s equations (Supplementary Information) for the lengths of the ellipsoid’s principal semi-axes ℓ1, ℓ2, and ℓ3. We can compute the Jacobian of Perrin’s equations, and solve for [ℓ1, ℓ2, ℓ3] by using nonlinear least squares method given a proper initial guess for the values.
Once we obtain the ellipsoid’s principal semi-axes [ℓ1, ℓ2, ℓ3] and orientation V, the covariance matrix C* of the ellipsoid is:
| (12) |
Having computed the covariance matrix C* by Eq.(12), we have now solved Eq.(6), and can therefore move to step 2 of our docking method.
Estimating the Covariance Matrix of a Molecule
In step 2 of our docking method, we propose to use a Newton-like method for minimization. Each iteration of a Newton-like minimization requires an evaluation of the target function and a computation of a descent step. Therefore, before we describe step 2, we first describe two algorithms that provide fast approximations to the function G(x), and by extension the Newton step. These approximations form the basis of step 2.
Quadratic Approximation
The first algorithm allows us to quickly compute the descent step for our minimization algorithm by finding a quadratic approximation of the covariance matrix near the current value x. We express the approximation as
| (13) |
where
| (14) |
i, j = 1, 2, 3, p ∈ ℝ3, κ is a constant, and K is a constant 3 × 3 matrix.
Let a1, … , ana be the surface points for M(x) that come from domain A and let b1, … , bnb be those that come from domain B, where na and nb are the number of points in domain A and domain B, respectively. Observe that the majority of the individual domain surface points remain part of the overall M(x) surface, since only the points where two domains contact each other disappear from the solvent-accessible surface of M(x). Therefore, the majority of the change in the covariance matrix comes from the fact that the bi points are shifted by x and not from the change in the set of surface points. The larger ||p|| is, the more we expect the set of the surface points to change, but at the same time the translation of points that remain on the surface also contributes a greater weight. Thus, we expect that we can estimate the covariance matrix well at x + p by simply adjusting the points b by p and recomputing the covariance matrix. Going through the algebra (see Supplementary Information) we get the solution:
| (15) |
| (16) |
for i, j = 1, 2, 3.
However the quadratic approximation is limited in its accuracy since it assumes that the surface points of M(x) are constant. In the next section we focus on deriving the second approximation method that is more accurate but at the cost of an additional computation.
Geometric Approximation of a Molecule’s Covariance Matrix
In this section we derive a method, called G fast, for approximating G that is more accurate than the quadratic approximation in the previous section, but computationally slower, because it redetermines the set of surface points. However it is still significantly faster than fully recomputing Richards’ molecular surface.
Recall that ELM requires the computation of the surface of the molecule. The method has been shown to be relatively fast when calculating the surfaces of different molecules. However, in the case of rigid docking, the shape of the domains does not change, so it is computationally wasteful to fully recompute the surface of the domains every time we want to evaluate G(x).
Since we assumed that the three-dimensional structure of the individual domains does not change as they come closer together, we compute the surfaces of the two molecules initially once and then adjust their surfaces as the molecules move closer and start colliding. We label the set of surface points of molecule A as SA, and the surface points of B as SB. The surface points of B + x are therefore written as SB + x, representing the fact that the surface points of B are shifted by x. The goal is to determine which surface points in SA and SB remain as part of the overall surface of the combined molecule, and which are no longer on the surface.
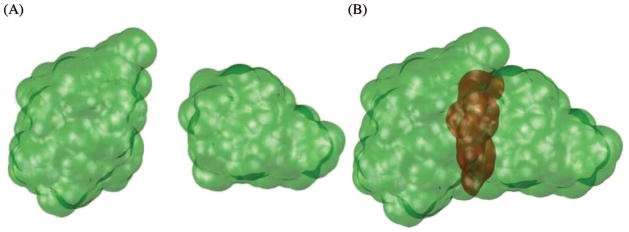
To figure out which surface points disappear in a collision we need to use a collision detection algorithm. Figure 1 illustrates that as two domains come closer together the surface points of one domain start colliding with the second domain, thus no longer participating in the definition of the combined solvent-accessible surface.
Figure 1.
Illustration of the two components of the Ub/UBA complex coming closer together, with the surface points computed with hydration layer thickness of 2.8Å. (A) The two molecules are apart so that all the surface points contribute to the overall surface (colored green). (B) The molecules come closer together, and some of the previous surface points (colored red) no longer contribute to the combined solvent-accessible surface.
We say that a surface point si ∈ Sa collides with B + x if there exists bj ∈ B + x such that the Euclidean distance between si and the center of bj is less than rj + h, where rj is the van der Waals radius of bj and h is the hydration layer thickness (set to 2.8Å in our case). We determine bj by a nearest neighbor search algorithm. Using the same procedure we also find the colliding points in Sb.
Let a1, … , ana be the set of points in SA that do not collide with B + x, and let b1, … , bnb be the set of points in SB + x that do not collide with A. The covariance matrix for the set a and b is computed as
| (17) |
for i, j = 1, 2, 3.
In the Results section we will show that the error introduced by this approximation is within the error introduced by our diffusion tensor prediction method ELM.
Step 2: From Equivalent Ellipsoid to Domain Position
Having developed approximate methods for rapid computation of the covariance matrix C*, we now describe step 2, where we find x* such that the covariance matrix of the surface points of M(x*) is equal to C*.
We use a Newton-like method to minimize , Eq.(9). Here we describe how we choose starting points, while the detailed description of the rest of the minimization method is given in Supplementary Information.
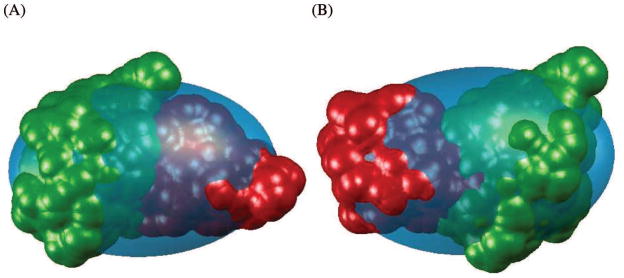
Every minimization method needs a starting point. Due to the symmetry inherent in the covariance matrix there are multiple local minimizers of . Figure 2 shows two local minimizers for the Ub/UBA complex; both have similar covariance matrices.
Figure 2.
Two local minimizers of for the Ub/UBA complex; both have similar covariance matrices of the surface points. The surface of the complex, with hydration layer thickness of 2.8Å, is drawn along with the equivalent PCAE for the specific solution, colored in aqua. Domain A is colored green and domain B is red. (A) The solution with the correct positioning of the second domain. (B) A solution with a similar covariance matrix, but incorrect domain placement.
We need to choose a starting point close to each of the local minimizers in order to make sure that we find the correct overall minimizer. To compute such a set of points, we replace the minimization problem given in Eq.(9) by an approximation where we only look at the diagonal elements:
| (18) |
Minimizing this new target function yields good starting points, since if we have a good model then
| (19) |
Still, is too complicated to easily be solved analytically. We therefore approximate it using Eqs.(13) and (14).
| (20) |
where
| (21) |
Setting the derivative of the quadratic to zero gives a maximum of eight solutions
| (22) |
We use these eight solutions as starting points for our minimization method (fully described in Supplementary Information).
Approximating Diffusion Tensor Under Translation
Matching the rotational diffusion tensor is just one of the many restraints that can be used to determine domain positioning. Usually the energy term from the diffusion tensor constraint should be combined with energy terms coming from other restraints. To avoid recomputing the diffusion tensor under every translation it is possible to solve Eq.(6) and use the solution to create a quadratic approximation of the energy value that can be used in the combined energy function.
We can quickly approximate , without recomputing the surface points, by quadratically approximating the predicted covariance matrix around the minimizers. The approximation will therefore give a good estimate of near the expected solution, which we assume is not far from x*, and monotonically increases in value as you move farther from the solution (which does not need to be computed accurately).
Given , the minimizers of χ2 derived using Algorithm 1, we compute the approximation of as
| (23) |
where i = 1, … , n.
Similarly we can approximate the diffusion tensor energy function χ2(xc) as
| (24) |
Results
To evaluate ELMDOCK, we applied it to several protein systems. Potential sources of inaccuracy in our docking approach are errors in the experimental relaxation data, structural noise, and the inaccuracy of ELM in predicting the diffusion tensor. To separate and quantify these errors we tested our method on two distinct datasets described below. For each complex, we separately tested docking with and without prior alignment/orientation of the individual domains based on their relaxation data (see 1). We refer to the ELMDOCK algorithm without the alignment procedure as ELMDOCK-t: this algorithm involves only translational degrees of freedom and holds the domain orientation the same as in the correct structure.
The first dataset, which we refer to as COMPLEX, is a set of 80 protein-protein complexes described in Mintseris et al.34 This dataset provides a wide variety of interprotein contacts and molecular shapes, but it contains no experimental relaxation data. For each complex we use ELM to generate a synthetic diffusion tensor Dsyn based on the already known 3D structure, and then predict for each NH vector in the molecule the synthetic ratio of relaxation rates ρsyn, which we subsequently use instead of ρexp as input for ROTDIF. This allows us to test our method under ideal conditions, when we are able to accurately predict the diffusion tensor for the whole complex.
The second dataset is a set of three proteins for which we have experimental diffusion tensor data: HIV-1 protease homodimer;35 Maltose-binding protein;36 and Ubiquitin/UBA complex.37 We use this dataset to examine the accuracy of the algorithm under real experimental conditions and the inaccuracies inherent in ELM’s prediction of the diffusion tensor.
Due to the four-fold ambiguity in the relative orientation of domain B with respect to A (see e.g.8) and the existence of multiple local minimizers (with regard to translation) for each orientation, we expect to have at least eight potential solutions.15 The solutions are ranked by the backbone RMSD between the experimental structure of the complex and the predicted one, where the atom positions in B are adjusted by R* and x* (recall that A is fixed in space). Only the results for the lowest-RMSD solution are shown in this paper. Since R* can be directly computed from the experimental relaxation data independent of the ELM model, we first focus our analysis on the minimizers that come from the correct orientation of the two domains. We then present the results for the complete docking method that also includes automatic alignment of the two domains, in addition to their positioning relative to each other.
We implemented ELMDOCK in MATLAB 7.8.0 and performed all calculations and timing on a single core of a 3.16 GHz Pentium Core 2 Duo E8500 processor with 3.25 GB of RAM, running Windows XP Service Pack 3. We stop each minimization in Step 2 when the change in x is less than 0.1Å. For robust regression we use the value of ω = 0.04E(ρexp) as the cutoff for the Talwar weighting function, where E(X) is the expected value of X.38
Docking Using Synthetic Data
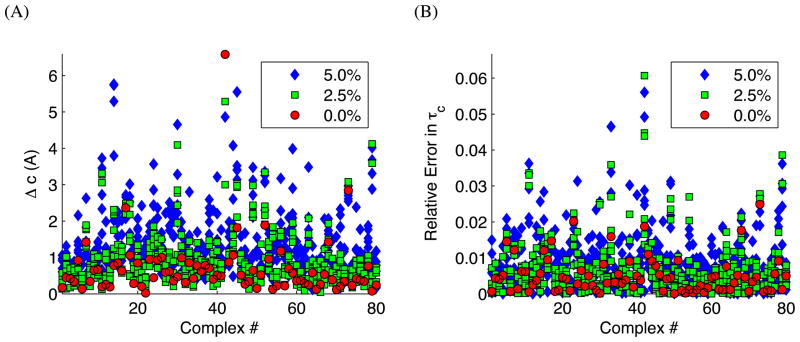
We use the COMPLEX dataset to demonstrate the correctness of the docking based on the approximation of the covariance matrix instead of full recomputation of the diffusion tensor. For each complex we generate a synthetic diffusion tensor Dsyn using ELM and then synthetic values for ρsyn. We then dock the complex using ELMDOCK-t, as detailed above, where we use ρsyn instead of ρexp. In practice, the measured ρexp values usually have experimental errors of 1 – 5%. To simulate the effect of these random errors on the quality of the solution, we also added normally distributed noise to ρsyn with a standard deviation of 2.5% or 5%. We will rate our results based on the “Δc”, the smallest distance between the original and all the predicted positions of the center of the second domain. To check that we dock within the accuracy of the ELM model we compute the relative error of the overall rotational correlation time . Figure 3 shows the results of docking with and without the random-noise errors in ρsyn.
Figure 3.
Docking results for the 80 protein complexes (from the COMPLEX dataset) based on synthetic data with no errors, 2.5%, and 5% random errors in ρsyn. (Due to technical issues with the surface-builder program SURF30,31 we removed four complexes from the original set of 84.) Docking of each complex was performed six times, with individual errors in randomly selected from the normal distribution. (A) The error, Δc, in positioning of the second domain relative to the first one. Several larger outliers for complex 42, 1I4D, not shown. (B) Relative error in the overall rotational correlation time, τc, between the predicted diffusion tensor at the known solution and at the docked solution.
These results demonstrate that we are able to effectively dock two domains using ELMDOCK-t given an accurate predictor of the diffusion tensor. For most proteins using the fast approximation Gfast yields a solution accurate to within 1.5Å. Moreover, the relative errors in the overall rotational correlation time (τc) (Figure 3B) are much smaller than the expected inaccuracy (10% on average, see29) of the diffusion tensor prediction using ELM. Therefore, we conclude that docking to a higher accuracy is unnecessary since our current approach is expected to only increase the error in τc by a negligible amount (less than 0.1%). Overall, these results show that our approach of using a quadratic approximation to derive a Newton-like descent step is adequate for minimizing .
It is noteworthy that in most cases, even with significant noise in ρexp values, our method is still able to converge to a correct solution within 1–2Å. The somewhat greater errors observed for a few complexes are due to the specific shapes and relative sizes of the domains, which makes the overall shape/diffusion tensor of the complex less sensitive to translation of one domain relative to the other. In these cases the inversion of Perrin’s equations needs to be computed to a higher accuracy than was set in the algorithm. The relative error in τc for all of the outliers is still much smaller than the expected inaccuracy of ELM, as shown in Figure 3B. See Supplementary Information for an illustration of the largest outlier, complex 42, 1I4D.
Docking Using Unbound Structures
In some docking applications structures of the individual components in the bound state might not be known in advance, but are to be determined in the process of docking, for example, using the “unbound” structures of the domains as the starting point. We therefore examine how accurately our method positions two domains relative to each other given only the relaxation data for the bound complex and the unbound structures of the two domains, i.e. how robust our method is with regard to structural rearrangements in the individual components resulting from binding interactions. We anticipate several additional sources of inaccuracy in the resulting complexes when using unbound structures of the individual components. These include (i) inaccuracy in the derived experimental diffusion tensor(s), due to a different orientation of the NH bond vectors, and (ii) a different 3D shape of each domain (and therefore of the complex), which would affect the predicted diffusion tensor.
Here we take advantage of the availability of both bound and unbound structures for the 80 proteins of the COMPLEX dataset.34 The ρsyn values generated for each bound complex as described above (zero noise) were used as input for ROTDIF, but applied to unbound structures of each domain. Using the NH bond vectors of the unbound structures and the synthetic ρexp, we computed the diffusion tensors of each of the unbound domains, and used the same docking procedure as above (ELMDOCK-t or ELMDOCK) to assemble the corresponding complex of the unbound individual components.
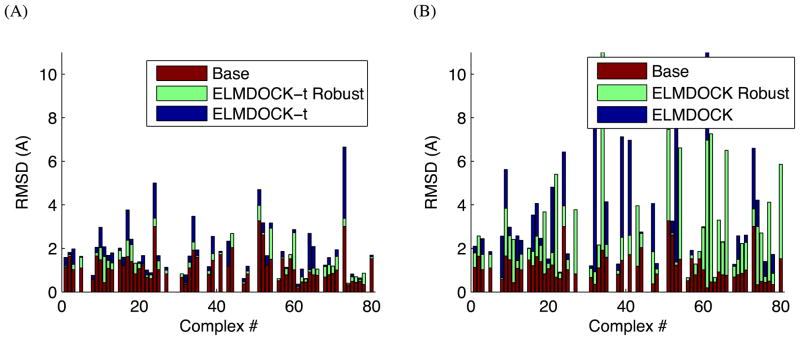
We compare the resulting structures (docked “unbound” complexes) with the corresponding complexes of the bound structures in Figure 4. The results are presented in terms of RMSDs for all backbone atoms. These numbers should be compared to the “Base” RMSD level (red bars in Figure 4) that reflects the structural differences between the unbound and bound structures of the individual domains, calculated by superimposing the unbound structure of each domain onto its bound structure in the complex and computing the overall (backbone) RMSD. The results show that structural/dynamic rearrangements in the individual components upon complex formation do not dramatically affect the relative domain positioning in the resulting diffusion-tensor-guided structures. The average error in the position of the second domain (Δc) for ELMDOCK-t was 2.1Å and 3.9Å for ELMDOCK.
Figure 4.
The results of (A) ELMDOCK-t and (B) ELMDOCK assembly of complexes of “unbound” structures of the proteins from the COMPLEX dataset, using ρ syn values, computed from the corresponding “bound” complexes, as the input experimental data to guide the docking. Shown are the backbone “Base” RMSDs (red bars) and RMSDs between the resulting (unbound) complex and the original (bound) complex. Missing bars correspond to those few complexes where we were unable to properly match the atoms between the bound and the unbound coordinate sets. The results are presented for robust and regular regression versions of ROTDIF (green and blue bars, respectively).
From Figure 4 we can see that using NH vectors from the unbound confirmations to derive the target experimental diffusion tensor for docking yields only a small increase in the RMSD error. For ELMDOCK-t the RMSD increased only by 0.70Å (2.59Å for ELMDOCK) from the “Base” RMSD, while using robust regression can further improve the solution to just a 0.32Å (1.64Å for ELMDOCK) increase in the RMSD. The greater increase in RMSD in ELMDOCK for some complexes is mostly due to the very large size of the domains, where even small error in orientation can generate a large RMSD.
These results indicate that the diffusion-tensor-guided docking is robust with respect to structural rearrangements induced by complex formation. Damping the contribution from outliers (as part of robust regression in ROTDIF) during the computation of the experimental diffusion tensor can additionally compensate for some of the errors induced by the conformational differences between the unknown bound and the known unbound structures, thus yielding a more accurate estimation of the target experimental diffusion tensor without a priori knowledge of the exact bound structure. Moreover, these findings also suggest that the unbound structures of the individual components could be used as a good initial approximation for the complex assembly, to be followed by more rigorous docking steps that allow structural flexibility and adaptation necessary for final adjustment of the individual components in the complex.
Application to Real Dual-Domain Systems
We tested our method on three two-component molecular systems for which the experimental overall rotational diffusion tensor is available: HIV-1 protease homodimer (Structure 1bvg); Maltose-binding protein (Structure 1ezp); and Ubiquitin/UBA complex (Structure 2jy6). Structure 1bvg is the first model from the PDB entry 1BVG,35 the experimental overall rotational diffusion tensor values are from Tjandra et al.39 Structure 1ezp is the first model from PDB entry 1EZP,36 the experimental rotational diffusion tensor values are from Ryabov and Fushman.23
In the case of Ubiquitin/UBA complex,37 both proteins contain extended unstructured and flexible tails. As in our previous study,15 in order to examine the effect of these tails on the outcome of docking, we created three different versions of this complex. Structure 2jy6 is the first model from the PDB entry 2JY6. Structure 2jy6-I is the Structure 2jy6, but with the tails of Ubiquitin and UBA replaced with 100 different sets of tail orientations in exactly the same way as in.15 Structure 2jy6-II is Structure 2jy6 with both tails clipped off. Finally, Structure 2jy6-III is the “unbound” version of the Ubiquitin/UBA complex, where we use the unbound tailless structures of ubiquitin (PDB entry 1D3Z) and UBA (PDB entry 2JY5) in place of their bound structures in Structure 2jy6. The overall backbone RMSD between Structure 2jy6-I and Structure 2jy6-III is 0.97Å.
For HIV-1 protease (1bvg) and Maltose-binding protein (1ezp) we only have the data for the diffusion tensor of the complex, so we only test these structures using ELMDOCK-t, i.e. we fix the interdomain orientation and only translate one of the domains based on the experimental diffusion tensor. For the Ubiquitin/UBA complex we have complete relaxation data and therefore use the complete method ELMDOCK, where the two proteins are first aligned and then optimally translated relative to each other.
Here we compare the computational efficiency of our method to the previous method,23 which we will refer to as “simplex”. We did not test our method against Ryabov et al.,25 but for convex problems simulated annealing is known to be inefficient. For this comparison, the initial guesses for the “simplex” minimization were generated using the method derived in section “Step 2: From Equivalent Ellipsoid to Domain Position”. The results for the three proteins are presented in Table I. The “simplex” and the ELMDOCK methods yield almost identical errors in domain positioning, therefore, the errors for “simplex” are omitted in the table. For all the structures tested we also confirmed that we are able to accurately dock them using synthetic relaxation data (data not shown).
Table I.
The results of diffusion-tensor-guided docking using ELMDOCK-t and ELMDOCK on experimental data.
| Structurea | Methodb | RMSDc | RMSD2d | Δce | Simplex Time(s)f | Time(s) | #Sol.g |
|---|---|---|---|---|---|---|---|
| 1bvg | ELMDOCK-t | 0.87 | 2.55 | 2.55 | 4052 | 5.09 | 2 |
| 1ezp | ELMDOCK-t | 1.63 | 5.00 | 5.00 | 3208 | 8.19 | 2 |
| 2jy6 | ELMDOCK-t | 1.72 | 4.49 | 4.49 | 1188 | 4.00 | 2 |
| 2jy6 | ELMDOCK | 3.26 | 6.69 | 4.93 | 5036 | 6.70 | 8 |
| 2jy6-I | ELMDOCK-t | 2.12h (1.10)i |
5.68h (2.58)i |
5.86h (2.58)i |
- (−) |
3.92h (0.00)i |
2h |
| 2jy6-I | ELMDOCK | 3.56h (0.85)i |
7.65h (2.16)i |
5.86h (2.57)i |
- (−) |
6.67h (0.00)i |
8h |
| 2jy6-II | ELMDOCK-t | 4.52 | 9.55 | 9.55 | 1164 | 3.66 | 2 |
| 2jy6-II | ELMDOCK | 5.43 | 11.63 | 10.58 | 4841 | 5.67 | 8 |
| 2jy6-III | ELMDOCK | 4.57 | 9.59 | 9.26 | 4576 | 6.53 | 8 |
2jy6-I is the ensemble of 100 structures representing various conformations of Ub and UBA tails (see text), whereas in 2jy6-II the tails were clipped off. 2jy6-III is a complex of the “unbound” tailless structures of Ub and UBA.
The method that was used to dock the complex.
The backbone RMSD (in Å) between the original complex structure and the predicted complex. The structures are optimally rotated and centered using the center of mass.
The backbone RMSD (in Å) between the coordinates of atoms of the second domain for the original and predicted complex.
The distance (in Å) between the original and the predicted center of the second domain. The center is computed as the average of the positions of all the atoms in the domain.
The time (in seconds) to dock the two domains using the method proposed in Ryabov and Fushman.23
The number of possible solutions, all of which have a very similar overall diffusion tensor.
Values are the means of the individual values for the best solution of each of the 100 models.
Values in the parentheses are the standard deviations of the individual values for the best solution of each of the 100 models.
We see from Table I that for rigid structures like 1bvg and 1ezp our docking resulted in a 5Å error in displacement. For a non-rigid complex like Ubiquitin/UBA, depending on the conformation of the tails, we get an average error of 5.8Å in displacement with a standard deviation of 2.6Å. Removing the tails increased the RMSD2 from 7.7Å to 10.6Å. This suggests that removing a flexible tail might not be an effective strategy for the diffusion tensor. As the tails contribute to the overall tumbling of the complex, it is very plausible that their effect does not average out completely in the relaxation data measured in solution, and that some form of “averaged” structure needs to be used instead. Using Structure 2jy6-III (the “unbound” version of the Ubiquitin/UBA complex) does not increase the error in our solution relative to Structure 2jy6-II, implying that the difference in conformations (bound versus free) of these proteins is not an important source of error, a fact that has also been observed for COMPLEX data set (Figure 4).
The comparison of ELMDOCK and ELMDOCK-t shows that alignment of the two domains based on their diffusion tensor does not significantly affect the RMSD2 of the optimal solution, suggesting that it is not a significant contributor of error. Overall, ELMDOCK is about 800 times faster than the method proposed previously.23 A close inspection of the runtimes revealed that about 200-fold speedup is the result of using a Newton-like algorithm instead of a simplex algorithm and the further 4-fold speedup is the result of using G fast instead of G as our covariance matrix prediction method.
Combining Rotational Diffusion Tensor with Alignment Tensor and Ambiguous Interface Related Restraints
In order to improve upon solutions in the previous section we introduce a novel docking energy function that combines the diffusion tensor-based restraints with the alignment tensor, CSP-based, and steric energy restraints from PATIDOCK+.15 The new energy function, , combines the energy function , from PATIDOCK+, with that of 23:
| (25) |
where ζ is a scaling factor that relates to the values in . In our experiments we set ζ = 1.27 × 10−5, based on the same approach as in.15 We use the branch and bound method40 to deterministically solve for the global minimum and call this method ELMPATIDOCK. We ran ELMPATIDOCK on Structure 2jy6-I (first model) and 2jy6-II; the results are presented in Table II.
Table II.
The results of docking using ELMPATIDOCK. See Table I for explanation of column headers.
| Structure | Methoda | RMSD | Δc | #Sol. |
|---|---|---|---|---|
| 2jy6 | ELMPATIDOCK | 0.99 | 1.97 | 1 |
| 2jy6-II | ELMPATIDOCK | 0.87 | 1.82 | 1 |
|
| ||||
| 2jy6 | ELMPATIDOCKb | 2.55 | 5.65 | 8 |
| 2jy6-II | ELMPATIDOCKb | 1.23 | 3.70 | 8 |
Diffusion tensors and alignment tensors gave slightly different orientational constraints. Alignment tensors were used to orient the two domains.
Contribution of the CSP-based and steric energy restraints were removed from the minimized energy function.
The ELMPATIDOCK solutions clearly show an improvement over the ELMDOCK solutions in Table I, or RDC-based PATIDOCK solutions (see15). For example, observe that ELMDOCK has better performance on Structure 2jy6, and on average even on Structure 2jy6-I (the ensemble of 100 structures) than on (tailless) Structure 2jy6-II. Conversely, PATIDOCK has better performance on Structure 2jy6-II than on Structure 2jy6. ELMPATIDOCK performs better than ELMDOCK or PATIDOCK on both structures. Table II also shows that the CSP-based restrains are necessary to break the degeneracy in the RDC and relaxation-based docking (see below for further discussion). The solution could further be improved by combining these restraints with a more comprehensive energy function, like the AMBER force field,41 or adding them to existing docking software. Note that the use of quadratic approximation of the covariance matrix in Eq.(23) was critical to the implementation of ELMPATIDOCK, since recomputing the covariance matrix of the surface at each energy function evaluation would be computationally impractical.
These results likely reflect the difference between the timescales of motions sensed by spin relaxation and RDCs. For example, modulations of the shape of a protein caused by large-amplitude motions of its tails (and/or flexible loops) are so fast compared to the characteristic timescale of the RDC averaging (nanoseconds to milliseconds) that the resulting alignment tensor, reflecting the averaged shape of the molecule, might not sense the presence of the tails. On the other hand, the tails’ motions are only somewhat faster than or comparable to the timescale (nanoseconds) relevant to the overall tumbling, and therefore the averaged diffusion tensor might be more sensitive to the presence of extended unstructured tails and their “average” conformation.
It is worth mentioning here that the degeneracies related to diffusion tensor-guided docking are generally of two types: (i) orientational degeneracy due to the intrinsic symmetry of the diffusion tensor, which has no directionality, i.e. cannot distinguish between the positive and negative eigenvector directions (e.g., Vi and −Vi) and (ii) due to the symmetry of the overall shape of the individual components or of their complex. The latter could result in an axially symmetric or even isotropic diffusion tensor or in the “translational degeneracy” (illustrated in Figure 2) due to close values of the tensor for two different relative positions of the individual components within a complex. Docking guided by RDCs has similar challenges (as shown in our previous study15), because the alignment tensor has the same symmetry properties as the diffusion tensor. Moreover, in the case of steric alignment caused by neutral planar objects, both tensors are defined by the shape of the molecule and therefore have similar orientations.42 Therefore, including RDC data might not help fully resolve the above mentioned degeneracies. However, these degeneracies can be resolved by adding information on intermolecular distances or contacts, even as ambiguous as the CSPs, because the latter do identify sites on the binding partners that form the interface and therefore are expected to resolve both orientational and positional degeneracies. Indeed, as shown in Table II, including CSP-based contact restraints into ELMPATIDOCK calculations removes the degeneracy of the resulting structures. Adding only CSP restraints to the diffusion-guided docking also resolves the degeneracy (data not shown), whereas having relaxation and RDC data and leaving out the CSPs does not.
Conclusions
We developed an efficient minimization method for rigid-body docking of two-component molecular complexes guided by the overall rotational diffusion tensor extracted from spin relaxation data. The improved efficiency of the method is a direct consequence of the two approximation methods that we developed for fast estimation of the diffusion tensor of a multi-component system. We combined the approximation methods into a novel two-step minimization protocol that provides the first complete deterministic method for docking molecular complexes based on the experimental NMR relaxation data and three-dimensional structure of the individual components. Our method finds the solution about 800 times faster than the previous (simplex-based) docking23 (which provides no method for determining the initial guess) and is expected to be significantly more computationally efficient than the simulated annealing method25 (which is not guaranteed to converge to the correct solution). The utility of the two approximation methods developed here goes beyond the specific application to ELMDOCK since they can be integrated into alternative docking methods or simulation software.
We demonstrated the robustness of our method to experimental noise and to errors in domain structures by docking a large variety of protein complexes using synthetic relaxation data with or without experimental errors. Using real experimental data on rigid structures like HIV-1 protease homodimer or maltose binding protein we are able to dock within a Δc of 5Å from the actual solution. For docking molecules containing partially unstructured flexible tails, deriving a properly “averaged” structure is important for getting a more accurate solution. However, the robustness of our approach with respect to structural rearrangements accompanying complex formation (especially when used in combination with robust regression ROTDIF) suggests that the diffusion-tensor-guided docking could be used effectively in the starting stages of molecular complex assembly, e.g., by starting with the unbound structures of the individual components, then using ELMDOCK/ELMPATIDOCK to develop an initial guess at the solution, and subsequently refining it as the computation progresses.
ELMDOCK, with the approximation methods for the diffusion tensor presented in this paper, can potentially be used in several ways. First, it provides a quick rigid-body docking method whose solutions can be utilized to significantly limit the search space (or at least the initial search space) of a more complicated flexible-docking algorithm e.g. using ELMDOCK to develop an initial guess at the solution and subsequently refining in later stages of assembly. Second, our approximate energy functions (see section “Approximating Diffusion Tensor Under Translation”) can be included as an additional term in a more general energy function that accounts for all other structure-related restraints such as distance and torsional angle restraints, hydrogen bonding, electrostatic and van der Waals potentials, etc. Moreover, the computational efficiency of the ELMDOCK method proposed here makes it feasible to perform diffusion-tensor-guided docking at each iteration step of a more complicated flexible-docking algorithm, for example by analyzing docking of multiple conformers at each minimization iteration. ELMDOCK or parts of the method can be incorporated in or improve computationally expensive parts of existing structure determination/refinement protocols (e.g. HADDOCK,43 XPLOR-NIH44). This integration into a more complicated method would allow us to account for side chain and backbone flexibility at the interface, as well as integrate other available experimental data. Specifically, recent XPLOR-NIH implementations25,26 can directly benefit from the techniques developed here.
It should be mentioned here that our current implementation of the shape-based docking approach assumes that the components of the complex tumble or orient together as one entity, thus implying a relatively tight complex. Accurate characterization of protein-protein complexes should account for contributions to the experimental data from the free components in dynamic equilibrium with the complex (see, for example,45). This is particularly important for weak macromolecular interactions resulting in transient complexes. Applications to such systems would require modification of the target functions used in this study, to include the contributions to experimental data from the free form of the interacting partners.
The fact that our docking method is extremely fast for two-component complexes opens up the possibility of extending the ELMDOCK approach to three or more components. Even though each additional component gives rise to an exponential increase in complexity and time, it is still possible to quickly approximate the diffusion tensor energy function for a multitude of components.
Supplementary Material
Acknowledgments
This work was supported by NIH grant GM065334 to D.F.. The ELMDOCK program is available from the authors upon request. See Supplementary Information for derivation of a covariance matrix of an ellipsoid, Perrin’s equations and their inverse, quadratic approximation of the molecule’s covariance matrix, and detailed description of the ELMDOCK minimization algorithm.
References
- 1.Tolman J, Flanagan J, Kennedy M, Prestegard J. Nuclear Magnetic Dipole Interactions in Field-oriented Proteins: Information for Structure Determination in Solution. Proceedings of the National Academy of Sciences. 1995;92:9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tjandra N, Bax A. Direct Measurement of Distances and Angles in Biomolecules by NMR in a Dilute Liquid Crystalline Medium. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 3.Bax A. Weak Alignment Offers New NMR Opportunities to Study Protein Structure and Dynamics. Protein Science. 2003;12:1–16. doi: 10.1110/ps.0233303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fischer M, Losonczi J, Weaver J, Prestegard J. Domain Orientation and Dynamics in Multidomain Proteins from Residual Dipolar Couplings. Biochemistry. 1999;38:9013–9022. doi: 10.1021/bi9905213. [DOI] [PubMed] [Google Scholar]
- 5.Skrynnikov N, Goto N, Yang D, Choy W, Tolman J, Mueller G, Kay L. Orienting Domains in Proteins Using Dipolar Couplings Measured by Liquid-state NMR: Differences in Solution and Crystal Forms of Maltodextrin Binding Protein Loaded with β-cyclodextrin. Journal of Molecular Biology. 2000;295:1265–1273. doi: 10.1006/jmbi.1999.3430. [DOI] [PubMed] [Google Scholar]
- 6.Dosset P, Hus J, Marion D, Blackledge M. A Novel Interactive Tool for Rigid-body Modeling of Multi-domain Macromolecules Using Residual Dipolar Couplings. Journal of Biomolecular NMR. 2001;20:223–231. doi: 10.1023/a:1011206132740. [DOI] [PubMed] [Google Scholar]
- 7.Varadan R, Walker O, Pickart C, Fushman D. Structural Properties of Polyubiquitin Chains in Solution. Journal of Molecular Biology. 2002;324:637–647. doi: 10.1016/s0022-2836(02)01198-1. [DOI] [PubMed] [Google Scholar]
- 8.Fushman D, Varadan R, Assfalg M, Walker O. Determining Domain Orientation in Macromolecules by Using Spin-relaxation and Residual Dipolar Coupling Measurements. Progress in Nuclear Magnetic Resonance Spectroscopy. 2004;44:189–214. [Google Scholar]
- 9.van Dijk A, Fushman D, Bonvin A. Various Strategies of Using Residual Dipolar Couplings in NMR-driven Protein Docking: Application to Lys48-linked Di-ubiquitin and Validation Against 15N-relaxation Data. Proteins: Structure, Function, and Bioinformatics. 2005;60:367–381. doi: 10.1002/prot.20476. [DOI] [PubMed] [Google Scholar]
- 10.Clore GM. Accurate and Rapid Docking of Protein-Protein Complexes on the Basis of Intermolecular Nuclear Overhauser Enhancement Data and Dipolar Couplings by Rigid Body Minimization. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:9021–9025. doi: 10.1073/pnas.97.16.9021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Clore GM, Schwieters CD. Docking of Protein-Protein Complexes on the Basis of Highly Ambiguous Intermolecular Distance Restraints Derived from 1HN/15N Chemical Shift Mapping and Backbone 15N-1H Residual Dipolar Couplings Using Conjoined Rigid Body/Torsion Angle Dynamics. Journal of the American Chemical Society. 2003;125:2902–2912. doi: 10.1021/ja028893d. [DOI] [PubMed] [Google Scholar]
- 12.Blackledge M. Recent Progress in The Study of Biomolecular Structure and Dynamics in Solution From Residual Dipolar Couplings. Progress in Nuclear Magnetic Resonance Spectroscopy. 2005;46:23–61. [Google Scholar]
- 13.Hu W, Wang L. Residual Dipolar Couplings: Measurements and Applications to Biomolecular Studies. Annual Reports of NMR Spectroscopy. 2006;58:232. [Google Scholar]
- 14.Berlin K, O’Leary DP, Fushman D. Improvement and analysis of computational methods for prediction of residual dipolar couplings. Journal of Magnetic Resonance. 2009;201:25–33. doi: 10.1016/j.jmr.2009.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berlin K, O’Leary DP, Fushman D. Structural Assembly of Molecular Complexes Based on Residual Dipolar Couplings. Journal of American Chemical Society. 2010;132:8961–8972. doi: 10.1021/ja100447p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bruschweiler R, Liao X, Wright P. Long-range motional restrictions in a multidomain zinc-finger protein from anisotropic tumbling. Science. 1995;268:886–889. doi: 10.1126/science.7754375. [DOI] [PubMed] [Google Scholar]
- 17.Tjandra N, Garrett D, Gronenborn A, Bax A, Clore G. Defining long range order in NMR structure determination from the dependence of heteronuclear relaxation times on rotational diffusion anisotropy. Nature Structural & Molecular Biology. 1997;4:443–449. doi: 10.1038/nsb0697-443. [DOI] [PubMed] [Google Scholar]
- 18.Fushman D, Xu R, Cowburn D. Direct Determination of Changes of Interdomain Orientation on Ligation: Use of the Orientational Dependence of 15N NMR Relaxation in Abl SH(32) Biochemistry. 1999;38:10225–10230. doi: 10.1021/bi990897g. [DOI] [PubMed] [Google Scholar]
- 19.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational Diffusion Anisotropy of Human Ubiquitin from 15N NMR Relaxation. Journal of the American Chemical Society. 1995;117:12562–12566. [Google Scholar]
- 20.Dosset P, Hus JC, Blackledge M, Marion D. Efficient Analysis of Macromolecular Rotational Diffusion from Heteronuclear Relaxation Data. Journal of Biomolecular NMR. 2000;16:23–28. doi: 10.1023/a:1008305808620. [DOI] [PubMed] [Google Scholar]
- 21.Ghose R, Fushman D, Cowburn D. Determination of the Rotational Diffusion Tensor of Macromolecules in Solution from NMR Relaxation Data with a Combination of Exact and Approximate Methods–Application to the Determination of Interdomain Orientation in Multidomain Proteins. Journal of Magnetic Resonance. 2001;149:204–217. doi: 10.1006/jmre.2001.2295. [DOI] [PubMed] [Google Scholar]
- 22.Walker O, Varadan R, Fushman D. Efficient and accurate determination of the overall rotational diffusion tensor of a molecule from 15N relaxation data using computer program ROTDIF. Journal of Magnetic Resonance. 2004;168:336–345. doi: 10.1016/j.jmr.2004.03.019. [DOI] [PubMed] [Google Scholar]
- 23.Ryabov Y, Fushman D. Structural Assembly of Multidomain Proteins and Protein Complexes Guided by the Overall Rotational Diffusion Tensor. Journal of the American Chemical Society. 2007;129:7894–7902. doi: 10.1021/ja071185d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fushman D, Cowburn D. Characterization of Inter-Domain Orientations in Solution Using the NMR Relaxation Approach. Protein NMR for the Millenium. Biological Magnetic Resonance. 2002;20:53–78. [Google Scholar]
- 25.Ryabov Y, Suh JY, Grishaev A, Clore GM, Schwieters CD. Using the Experimentally Determined Components of the Overall Rotational Diffusion Tensor To Restrain Molecular Shape and Size in NMR Structure Determination of Globular Proteins and Protein-Protein Complexes. Journal of the American Chemical Society. 2009;131:9522–9531. doi: 10.1021/ja902336c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ryabov Y, Clore G, Schwieters C. Direct Use of 15N Relaxation Rates as Experimental Restraints on Molecular Shape and Orientation for Docking of Protein-Protein Complexes. J Am Chem Soc. 2010;132:5987–5989. doi: 10.1021/ja101842n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carrasco B, de la Torre JG. Hydrodynamic Properties of Rigid Particles: Comparison of Different Modeling and Computational Procedures. Biophysical Journal. 1999;76:3044–3057. doi: 10.1016/S0006-3495(99)77457-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.de la Torre JG, Huertas ML, Carrasco B. HYDRONMR: Prediction of NMR Relaxation of Globular Proteins from Atomic-Level Structures and Hydrodynamic Calculations. Journal of Magnetic Resonance. 2000;147:138 – 146. doi: 10.1006/jmre.2000.2170. [DOI] [PubMed] [Google Scholar]
- 29.Ryabov Y, Geraghty C, Varshney A, Fushman D. An Efficient Computational Method for Predicting Rotational Diffusion Tensors of Globular Proteins Using an Ellipsoid Representation. Journal of the American Chemical Society. 2006;128:15432–15444. doi: 10.1021/ja062715t. [DOI] [PubMed] [Google Scholar]
- 30.Varshney A, Brooks F, Jr, Wright WV. Linearly Scalable Computation of Smooth Molecular Surfaces. IEEE Computer Graphics and Applications. 1994;14:19–25. [Google Scholar]
- 31.Varshney A, Brooks F., Jr Fast Analytical Computation of Richard’s Smooth Molecular Surface. IEEE Visualization’93 Proceedings. 1993:300–307. [Google Scholar]
- 32.Perrin F. Mouvement Brownien d’un ellipsoide (I). Dispersion dielectrique pour des molecules ellipsoidales. Le Journal de Physique. 1934;5:497–511. [Google Scholar]
- 33.Perrin F. Mouvement Brownien d’un ellipsoide (II). Rotation libre et depolarisation des fluorescences. Translation et diffusion de molecules ellipsoidales. Le Journal de Physique. 1936;7:1–11. [Google Scholar]
- 34.Mintseris J, Wiehe K, Pierce B, Anderson R, Chen R, Janin J, Weng Z. Protein–protein Docking Benchmark 2.0: An Update. Proteins. 2005;60:214–216. doi: 10.1002/prot.20560. [DOI] [PubMed] [Google Scholar]
- 35.Yamazaki T, Hinck AP, Wang YX, Nicholson LK, Torchia DA, Wingfield P, Stahl SJ, Kaufman JD, Chang CH, Domaille PJ, Lam PY. Three-dimensional solution structure of the HIV-1 protease complexed with DMP323, a novel cyclic urea-type inhibitor, determined by nuclear magnetic resonance spectroscopy. Protein Science. 1996;5:495–506. doi: 10.1002/pro.5560050311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mueller GA, Choy W, Yang D, Forman-Kay JD, Venters RA, Kay LE. Global Folds of Proteins with Low Densities of NOEs Using Residual Dipolar Couplings: Application to the 370-residue Maltodextrin-binding protein. Journal of Molecular Biology. 2000;300:197–212. doi: 10.1006/jmbi.2000.3842. [DOI] [PubMed] [Google Scholar]
- 37.Zhang D, Raasi S, Fushman D. Affinity Makes the Difference: Nonselective Interaction of the UBA Domain of Ubiquilin-1 with Monomeric Ubiquitin and Polyubiquitin Chains. Journal of Molecular Biology. 2008;377:162–180. doi: 10.1016/j.jmb.2007.12.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.O’Leary DP. Robust Regression Computation Using Iteratively Reweighted Least Squares. SIAM Journal on Matrix Analysis and Applications. 1990;11:466–480. [Google Scholar]
- 39.Tjandra N, Wingfield P, Stahl S, Bax A. Anisotropic Rotational Diffusion of Perdeuterated HIV protease from 15N NMR Relaxation Measurements at Two Magnetic Fields. Journal of Biomolecular NMR. 1996;8:273–284. doi: 10.1007/BF00410326. [DOI] [PubMed] [Google Scholar]
- 40.Lawler E, Wood D. Branch-and-bound methods: A Survey. Operations Research. 1966;14:699–719. [Google Scholar]
- 41.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. Journal of the American Chemical Society. 1995;117:5179–5197. [Google Scholar]
- 42.de Alba E, Baber JL, Tjandra N. The Use of Residual Dipolar Coupling in Concert with Backbone Relaxation Rates to Identify Conformational Exchange by NMR. Journal of the American Chemical Society. 1999;121:4282–4283. [Google Scholar]
- 43.Dominguez C, Boelens R, Bonvin A. HADDOCK: A Protein-protein Docking Approach Based on Biochemical or Biophysical Data. Journal of the American Chemical Society. 2003;125:1731–1737. doi: 10.1021/ja026939x. [DOI] [PubMed] [Google Scholar]
- 44.Schwieters C, Kuszewski J, Tjandra N, Marius Clore G. The Xplor-NIH NMR Molecular Structure Determination Package. Journal of Magnetic Resonance. 2003;160:65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- 45.Ortega-Roldan JL, Jensen MR, Brutscher B, Azuaga AI, Blackledge M, van Nuland NAJ. Accurate Characterization of Weak Macromolecular Interactions by Titration of NMR Residual Dipolar Couplings: Application to the CD2AP SH3-C:Ubiquitin Complex. Nucleic Acids Research. 2009;37:e70. doi: 10.1093/nar/gkp211. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.