FIG. 3.

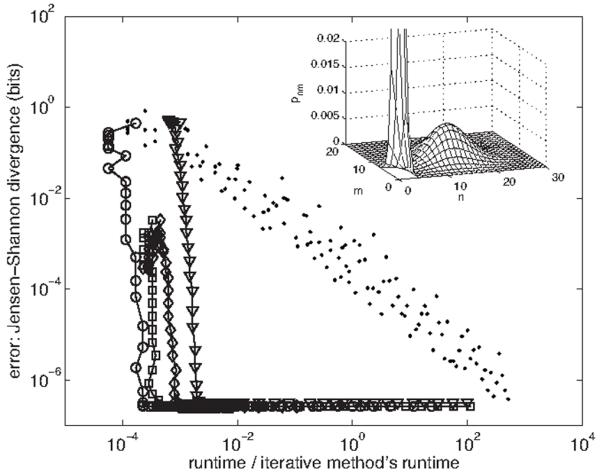
Error vs runtime for the spectral method and stochastic simulation. Error is the Jensen-Shannon divergence [41] between p_nm obtained using the |n,m〉 basis (via iterative solution of the original master equation) and that obtained using the |j,k〉 basis [circles; cf. Eq. (80)], the |j,k_j〉 basis [triangles; cf. Eq. (90)], the |n,k_n〉 basis [squares; cf. Eq. (100)], the |j,k_n〉 basis [diamonds; cf. Eq. (114)], or stochastic simulation [28] (dots). Runtimes are scaled by that of the iterative solution, 150 s (in matlab). Spectral basis data is obtained by varying K, the cutoff in the eigenmode number k of the second gene; simulation data is obtained by varying the integration time. The input distribution $p_n={\pi }_1{e}^{-{\lambda }_1}{\lambda }_1^n∕n!+(1-{\pi }_1)e^{-{\lambda }_2}{\lambda }_2^n∕n!$ [from which g_n is calculated via Eq. (59)] is a mixture of two Poisson distributions with λ₁=0.5, λ₂=15, and π₁=0.5. The regulation function $q_n=q_{-}+(q_{+}-q_{-})n^{\nu }∕(n^{\nu }+n_0^{\nu })$ is a Hill function with q₋=1, q₊=11, n₀=7, and ν=2. The gauge choices used (cf. Fig. 2) are g‾=Σ_n p_ng_n, q‾=Σ_n p_nq_n, q‾_n=q_n, and q‾_j=Σ_n〈j|n〉q_n〈n|j〉. The cutoffs used are J=80 for the eigenmode number j of the first gene and N=50 for the protein numbers n and m. Inset: the joint probability distribution p_nm. The peak at low protein number extends to p₀₀≈0.1.