Figure 1.

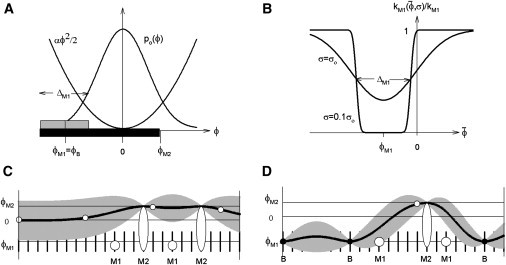
Aspects of a continuous-flexible-chain regulatory model with two-step myosin binding. (A) Azimuthal orientations ϕ of the binding site on actin for weak myosin binding (shaded box of width Δ_M1, centered on ϕ_M1 < 0), followed by a wider site for strong myosin binding (shaded box, out to angle ϕ_M > 0). The weak-binding site can be shared with troponin-I, so ϕ_M1 = ϕ_B, the blocking angle observed for the tropomyosin chain at low calcium. The chain is confined near-zero angle by a quadratic potential so that, at high calcium without bound myosins, the chain fluctuates ∼ϕ = 0 with a Gaussian distribution p_o(ϕ) of width σ_o (the closed state). If the chain is pinned nearby, it will fluctuate about a nonzero mean $\overline{\varphi }$ with a reduced standard deviation σ < σ_o. (B) The myosin binding rate k_M1($\overline{\varphi },$σ) is proportional to the probability that the chain avoids the weak-binding site, which varies with the local mean and SD of the chain as shown. Rate inhibition is most pronounced when the chain is held over the weak site by TnI, when σ will be small (e.g., σ = 0.1σ_o as shown). (C and D) Cartoons of azimuthal chain angles along F-actin (solid line = mean angle, shading = deviations out to ±σ, vertical ticks = weak-binding actin sites). (C) The high-calcium configuration with bound myosins as shown (M1 = weak, M2 = strong). The chain avoids all bound myosins, but M2 myosins trap the chain at angles beyond ϕ_M (the myosin state) because its initial angular distribution lies above ϕ_B. (D) The low calcium configuration, where the chain is pinned at the blocking angle by TnIs bound to actin (open circles on the chain = detached TnI, solid circles = bound TnI). Myosin can bind into state M1 only where the chain has moved to higher angles, firstly by detachment of TnIs and then by M2 myosins. Chain configurations were calculated from formulae in Appendix B in the Supporting Material.