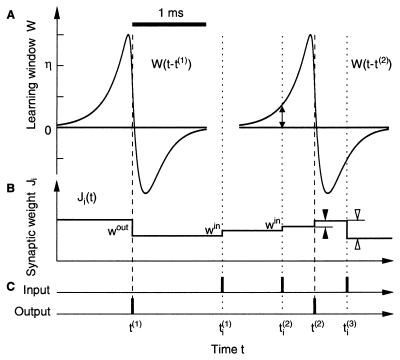
Figure 2.

Spike-based learning. (A) Two plots of the learning window W in units of the learning parameter η as a function of the temporal difference between spike arrival at time t at synapse i (e.g., t = t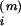, m = 1, 2, 3; dotted lines) and postsynaptic firing at times t⁽¹⁾ and t⁽²⁾ (dashed lines). Scale bar = 1 ms. (B) Time course of the synaptic weight J_i(t) evoked through input spikes at synapse i and postsynaptic output spikes (vertical bars in C). The output spike at time t⁽¹⁾ decreases J_i by an amount w^out. 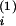The input at t and t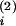 increase J_i by wⁱⁿ each. There is no influence of the learning window W because these input spikes are too far away in time from t⁽¹⁾. The output spike at t⁽²⁾, however, follows the input at t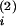 closely enough, so that, at t⁽²⁾, J_i is changed by w^out < 0 plus W(t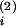 − t⁽²⁾) > 0 (double-headed arrow), the sum of which is positive (filled arrowheads). Similarly, the input at t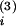 leads to a decrease wⁱⁿ + W(t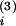 − t⁽²⁾) < 0 (open arrowheads). The assumption of instantaneous and discontinuous weight changes can be relaxed to delayed and continuous ones that are triggered by spikes, provided weight changes are fast when compared with the time scale of learning (46). 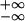If the integral ∫W(s) ds is sufficiently negative, then one can drop w^out (49).