Table 1. Predictive methods, input variables and critical equations.
| Method | Variable name | Methodology | Input variables | Critical equations |
| ACSM-walk | ACSM | Statistical | Velocity (v), body mass (m), regression coefficients |
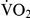 = (0.1v+0.0583)m = (0.1v+0.0583)m |
| Force production | EXT-FP | Measured, calculated, statistical | Body mass, velocity, ground contact time |
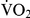 = ƒ (vm/contact time) = ƒ (vm/contact time) |
| CoM-GRF | EXT-GRF | Measured, calculated | Ground reaction forces, body mass, acceleration (a) | F = mav = ∫a dtEnergy = mgh+0.5mv2External work = ∑ dEnergy (time) |
| CoM-sacrum-model | EXT-MAT | Simulated | Velocity, body mass, segment lengths, angles | x = ƒ (segment length, angles)v = dx/dtEnergy = mgh+0.5mv2External work = ∑ dEnergy (time) |
| CoM- sacrum-measured | EXT-SAC | Measured, calculated | Motion of sacrum (x), body mass | v = dx/dtEnergy = mgh+0.5mv2External work = ∑ dMEnergy (time) |
| Internal work | INT-MAT | Simulated | Velocity, angular velocity (ω), segment lengths, angles, segment mass and moments of inertia (I) | Energy = ∑ 0.5 (mv2 + Iω2)(of segments)Internal work = ∑ dEnergy (time) |
| Joint moments | COMB-JM | Measured, calculated | Ground reaction forces (F), joint shape (r/R), motion of ankle, knee and hip joints | Muscle force = r/R FPower = Muscle force * vCombined work = ∑ Power/time (of joints) |
| Model (int + ext work) | COMB-MAT | Simulated, calculated | Internal (INT-MAT) and external (EXT-MAT) work | Combined work = internal +external work |
Note that the ACSM method is a metabolic energy approach while others are mechanical energy approaches. The mechanical energy approaches are grouped into those the approximate external work (the energy required to move the body), internal work (the energy required to move the legs relative to the body) and combined work (external and internal work).
