Abstract
We consider the problem of efficiently encoding a signal by transforming it to a new representation whose components are statistically independent. A widely studied linear solution, known as independent component analysis (ICA), exists for the case when the signal is generated as a linear transformation of independent nongaussian sources. Here, we examine a complementary case, in which the source is nongaussian and elliptically symmetric. In this case, no invertible linear transform suffices to decompose the signal into independent components, but we show that a simple nonlinear transformation, which we call radial gaussianization (RG), is able to remove all dependencies. We then examine this methodology in the context of natural image statistics. We first show that distributions of spatially proximal bandpass filter responses are better described as elliptical than as linearly transformed independent sources. Consistent with this, we demonstrate that the reduction in dependency achieved by applying RG to either nearby pairs or blocks of bandpass filter responses is significantly greater than that achieved by ICA. Finally, we show that the RG transformation may be closely approximated by divisive normalization, which has been used to model the nonlinear response properties of visual neurons.
1 Introduction
Processing of signals is often facilitated by transforming to a representation in which individual components are statistically independent. In such a natural coordinate system, the components of the signal may be manipulated, transmitted, or stored more efficiently. It has been proposed that this principle also plays an important role in the formation of biological perceptual systems (Attneave, 1954; Barlow, 1961).
The problem of deriving an appropriate transformation to remove dependencies of a given source, based on the statistics of observed samples, has been studied for more than a century. The classical solution, principal components analysis (PCA), is a linear transformation derived from the second-order signal statistics (i.e., the covariance structure). Although it may be computed for any source with finite variance, it typically fails to eliminate dependencies for nongaussian sources. Over the past 20 years, a more general method, known as independent component analysis (ICA), has been developed to handle the case when the signal is formed as a linear transformation of independent nongaussian sources. Again, the solution is a linear transformation that is derived from statistical properties of the source. ICA methods have shown success in many applications, especially in deriving bases for natural signals (Olshausen & Field, 1996; van der Schaaf & van Hateren, 1996; Bell & Sejnowski, 1997; Lewicki, 2002). As with PCA, the ICA transformations may be computed for most sources, but they are guaranteed to eliminate dependencies only when the assumed source model is correct. And even where the methodology seems to produce a sensible solution, the components of the resulting representation may be far from independent. A case in point is that of natural images, for which derived ICA transformations consist of localized oriented basis functions that appear similar to the receptive field descriptions of neurons in mammalian visual cortex (Olshausen & Field, 1996; Bell & Sejnowski, 1997; van Hateren & Ruderman, 1998). Although dependency between the responses of such linear basis functions is reduced compared to that of the original pixels (Zetzsche & Schönecker, 1987), such reduction is only slightly more than that achieved with decorrelation methods such as PCA (Bethge, 2006). Furthermore, ICA coefficients (or the responses of similar oriented filters) for natural images exhibit striking higher-order dependencies (Wegmann & Zetzsche, 1990; Zetzsche, Wegmann, & Barth, 1993; Simoncelli, 1997; Buccigrossi & Simoncelli, 1999).
Here, we consider the dependency elimination problem for the class of source models known as elliptically symmetric densities (ESDs). For ESDs, linear transforms have no effect on the dependencies beyond second order, and thus ICA decompositions offer no advantage over second-order decorrelation methods such as PCA. We introduce an alternative nonlinear procedure, which we call radial gaussianization (RG), whereby the norms of whitened signal vectors are nonlinearly adjusted to ensure that the resulting output density is a spherical gaussian, whose components are thus statistically independent. We apply our methodology to natural images, whose local statistics have been modeled by a variety of different ESDs (Zetzsche & Krieger, 1999; Wainwright & Simoncelli, 2000; Huang & Mumford, 1999; Parra, Spence, & Sajda, 2001; Hyvärinen, Hoyer, & Inki, 2001; Srivastava, Liu, & Grenander, 2002; Sendur & Selesnick, 2002; Portilla, Strela, Wainwright, & Simoncelli, 2003; Teh, Welling, & Osindero, 2003; Gehler & Welling, 2006). We show that RG produces much more substantial reductions in dependency, as measured with multi-information of pairs or blocks of nearby bandpass filter responses, than does ICA. Finally, we show that the RG transformation may be closely approximated by divisive normalization (DN), which was developed as a description of the nonlinear response properties of visual neurons (Heeger, 1992; Geisler & Albrecht, 1992), and which has been shown empirically to reduce higher-order dependencies in multiscale image representations (Malo, Navarro, Epifanio, Ferri, & Artigas, 2000; Schwartz & Simoncelli, 2001; Wainwright, Schwartz, & Simoncelli, 2002; Valerio & Navarro, 2003; Gluckman, 2006; Lyu & Simoncelli, 2007). Thus, RG provides a more principled justification of these previous empirical results in terms of a specific source model. Preliminary versions of this work have been presented in Lyu and Simoncelli (2009).
2 Eliminating Dependencies with Linear Transforms
We seek a transformation that maps a source signal drawn from a known density to a new representation whose individual components are statistically independent. In general, the density transformation problem is highly underconstrained: an infinite number of transformations can map a random variable associated with some input density into one associated with a given target density, and the problem only becomes worse as the dimensionality of the space increases.
A natural means of handling the nonuniqueness of this problem is to restrict the transformation to be linear. Linear transforms are particularly easy to work with and are often able to substantially reduce the complexity and improve the tractability of optimization problems. However, this comes at the expense of strong limitations on the set of source models that can be exactly factorized. In the following sections, we review linear solutions to the problem of dependency elimination, while emphasizing the underlying source model assumptions.
2.1 Multi-Information
We quantify the statistical dependency for multivariate sources using multi-information (MI) (Studeny & Vejnarova, 1998), which is defined as the Kullback-Leibler divergence (Cover & Thomas, 2006) between the joint distribution and the product of its marginals:
| (2.1) |
where H(x⃗) = ∫ p(x⃗) log (p(x⃗)) dx⃗ is the differential entropy of x⃗, and H(xk) denotes the differential entropy of the kth component of x⃗. If the logs are computed in base 2, these entropy quantities are expressed in units of bits. In two dimensions, MI is simply the mutual information between the two components (Cover & Thomas, 2006).1 As a measure of statistical dependency among the elements of x⃗, MI is nonnegative and is zero if and only if the components of x⃗ are mutually independent. Furthermore, MI is invariant to any operation performed on individual components of x⃗ (e.g., element-wise rescaling) since such operations produce an equal effect on the two terms in equation 2.1.
When x⃗ has finite second-order statistics, MI may be further decomposed into two parts, representing second-order and higher-order dependencies (Cardoso, 2004):
| (2.2) |
where Σ is the covariance matrix of x⃗, defined as E((x⃗ − Ex⃗)(x⃗ − Ex⃗)T), and
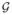 (x⃗) and
(x⃗) and
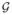 (xk) are gaussian densities with the same mean and covariance as x⃗ and xk, respectively.2
(xk) are gaussian densities with the same mean and covariance as x⃗ and xk, respectively.2
2.2 Principal Components Analysis and Whitening
For a gaussian signal x⃗, PCA provides a complete solution for the dependency elimination problem (Jolliffe, 2002). Assuming that x⃗ has zero mean, one computes the covariance matrix, Σ = E{x⃗x⃗T} and factorizes it as Σ =
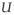 Λ
Λ
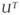 , where
, where
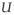 is an orthonormal matrix containing the eigenvectors of Σ and Λ is a diagonal matrix containing the corresponding eigenvalues. The covariance matrix of the PCA-transformed signal, x⃗pca =
is an orthonormal matrix containing the eigenvectors of Σ and Λ is a diagonal matrix containing the corresponding eigenvalues. The covariance matrix of the PCA-transformed signal, x⃗pca =
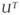 x⃗, is equal to Λ, and the second-order terms of the multi-information (defined in equation 2.2) will cancel, since the determinant of a diagonal matrix is the product of the diagonal elements. For a gaussian density, the higher-order terms of equation 2.2 are zero, and thus the PCA transform completely eliminates the statistical dependencies in x⃗ (i.e., I (x⃗pca) = 0). PCA may be followed by a linear “whitening” step in which each component is rescaled by its standard deviation: x⃗wht = Λ−1/2
x⃗, is equal to Λ, and the second-order terms of the multi-information (defined in equation 2.2) will cancel, since the determinant of a diagonal matrix is the product of the diagonal elements. For a gaussian density, the higher-order terms of equation 2.2 are zero, and thus the PCA transform completely eliminates the statistical dependencies in x⃗ (i.e., I (x⃗pca) = 0). PCA may be followed by a linear “whitening” step in which each component is rescaled by its standard deviation: x⃗wht = Λ−1/2
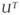 x⃗. A two-dimensional illustration of this two-step whitening procedure is illustrated in the left column of Figure 1. If the original signal is gaussian, the whitened signal will be a spherical gaussian with unit variance for each component. PCA or whitening may be applied to any nongaussian source with finite second-order statistics. In such cases, the second-order dependencies will be eliminated, but the higher-order dependencies in equation 2.1 may remain.
x⃗. A two-dimensional illustration of this two-step whitening procedure is illustrated in the left column of Figure 1. If the original signal is gaussian, the whitened signal will be a spherical gaussian with unit variance for each component. PCA or whitening may be applied to any nongaussian source with finite second-order statistics. In such cases, the second-order dependencies will be eliminated, but the higher-order dependencies in equation 2.1 may remain.
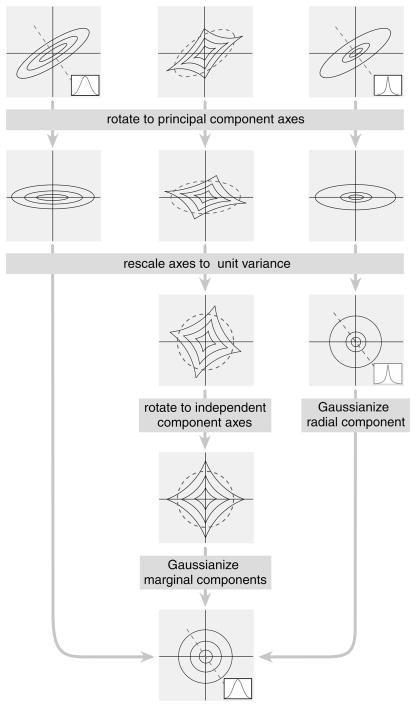
Figure 1.
Three methods of dependency elimination and their associated source models, illustrated in two dimensions. Dashed ellipses indicate covariance structure. Inset graphs are slices through the density along the indicated (dashed) line. (Left) PCA/whitening a gaussian source. The first transformation rotates the coordinates to the principal coordinate axes of the covariance ellipse, and the second rescales each axis by its standard deviation. The output density is a spherical, unit-variance gaussian. (Middle) Independent component analysis, applied to a linearly transformed factorial density. After whitening, an additional rotation aligns the source components with the Cartesian axes of the space. Last, an optional nonlinear marginal gaussianization can be applied to each component, resulting in a spherical gaussian. (Right) Radial gaussianization, applied to an elliptically symmetric nongaussian density, maps the whitened variable to a spherical gaussian.
2.3 Independent Component Analysis
Linear transformations are sufficient to remove statistical dependencies in gaussian variables and may be efficiently computed. A natural question is whether there is a class of nongaussian densities that can also be factorized with linear transforms. Consider a source that is formed by linearly transforming a signal with independent components, x⃗ = Ms⃗, where M is an invertible square matrix,3 and the density of s⃗ is factorial: p(s⃗) = Πk p(sk). Clearly, M−1 is a linear transformation that maps x⃗ into the original independent sources, s⃗. Given samples of x⃗, the general procedure for finding a linear transform that removes or reduces statistical dependency in x⃗ is known as independent components analysis (ICA) (Comon, 1994; Bell & Sejnowski, 1997; Cardoso, 1999).
A standard ICA methodology arises from decomposing the linear transform M using the singular value decomposition, M =
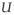 ΛVT. As with PCA, the matrices
ΛVT. As with PCA, the matrices
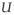 and Λ may be estimated from the covariance matrix of the data and used to whiten the data: x⃗wht = Λ−1/2
and Λ may be estimated from the covariance matrix of the data and used to whiten the data: x⃗wht = Λ−1/2
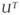 x⃗. The matrix V may then be chosen to minimize the MI of the whitened data x⃗wht:
x⃗. The matrix V may then be chosen to minimize the MI of the whitened data x⃗wht:
Since the second term does not depend on V, the optimization is performed only over the first term, which is the sum of the transformed marginal entropies. While some ICA algorithms optimize this objective directly (Learned-Miller & Fisher, 2000), most choose instead to optimize the expected value of a higher-order contrast function to avoid the difficulties associated with entropy estimation (Comon, 1994; Bell & Sejnowski, 1997; Cardoso, 1999). After the linear ICA transformation has factorized the source density, one may apply a marginal gaussianization procedure, nonlinearly mapping each component to have a unit-variance gaussian density using 1D histogram transforms (e.g., Chen & Gopinath, 2000). If the original density was a linearly transformed factorial density, the result of ICA followed by marginal gaussianization will be a spherical gaussian. Similar to PCA, ICA can be applied to an arbitrary source as long as the covariance and the higher-order contrast function exist. However, the result is guaranteed to be independent only when the signal actually comes from a linearly transformed factorial density. A two-dimensional illustration of the ICA procedure is shown in the middle column of Figure 1.
3 Eliminating Dependencies in Elliptical Symmetric Sources
PCA and ICA have been successfully applied to a wide range of problems across diverse disciplines. However, if our goal is to remove statistical dependency from a signal, PCA and ICA are not necessarily the right choices for sources that are not linearly transformed factorial densities. Here, we consider dependency elimination methods for the elliptically symmetric density models.
3.1 Elliptically Symmetric Densities
A d-dimensional random vector x⃗ has an elliptically symmetric density (ESD) if all surfaces of constant probability are ellipsoids that are parameterized by a symmetric positive-definite matrix Σ. In particular, an ESD with zero mean may be written
where f(·) is a positive-valued generating function satisfying (Fang, Kotz, & Ng, 1990). The normalizing constant α is chosen so that the density integrates to one. For a given matrix Σ, p(x⃗) is completely determined by the generating function f (·). Note that when x⃗ has finite second-order statistics, the covariance matrix will be a multiple of Σ. As a result, when x⃗ is whitened, the density of x⃗wht is a spherically symmetric density (SSD, also known as isotropic density), whose level surfaces are hyperspheres in the d-dimensional space (see the right column in Figure 1).
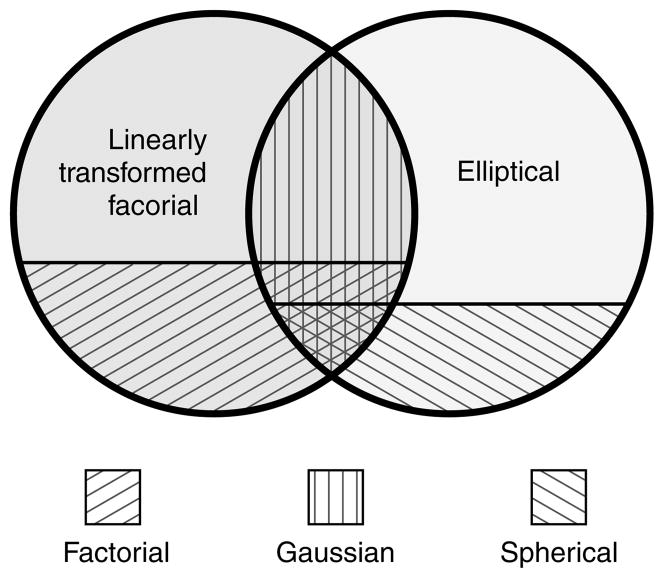
When the generating function, f, is an exponential, the resulting ESD is a multivariate gaussian with zero mean and covariance matrix Σ. The same gaussian variable x⃗ can also be regarded as a linear transformation of d independent gaussian components s⃗ = (s1, …, sd)T, each of which has zero mean and unit variance, as x⃗ = Σ−1/2s⃗. In general, gaussians are the only densities that are both elliptically symmetric and linearly decomposable into independent components (Nash & Klamkin, 1976). In other words, the gaussian densities correspond to the intersection of the ESDs and the linearly transformed factorial densities. Restricting this further, a spherical gaussian is the only density that is both spherically symmetric and factorial (i.e., with independent components). The relationships of gaussians, ESDs, and the linearly transformed factorial densities may be summarized with a Venn diagram, as shown in Figure 2.
Figure 2.
Venn diagram of the relationship between density models. The two circles represent the two primary density classes considered in this article: linearly transformed factorial densities and elliptically symmetric densities (ESDs). The intersection of these two classes is the set of all gaussian densities. The factorial densities (i.e., joint densities whose components are independent) form a subset of the linearly transformed factorial densities, and the spherically symmetric densities (SSDs) form a subset of the ESDs.
Besides gaussians, the ESD family also includes a variety of known densities and density families. Some of these have heavier tails than gaussians, such as the multivariate Laplacian, the multivariate Student’s t, and the multivariate Cauchy. More general leptokurtotic ESD families include the α-stable variables (Nolan, 2009) and the gaussian scale mixtures (GSM) (Kingman, 1963; Yao, 1973; Andrews & Mallows, 1974). The ESDs also include densities with lighter tails than a gaussian, such as the uniform density over the volume of a d-dimensional hyperellipsoid.
3.2 Linear Dependency Reduction for ESDs
As described in section 2, linear transforms can be used to remove statistical dependencies of gaussians, as well as the more general class of linearly transformed factorial densities. But apart from the special case of the gaussian, they cannot eliminate the dependencies found in ESDs. Specifically, if x⃗ has an ESD, we can remove the second-order dependencies of equation 2.2 with a linear whitening operation, thereby transforming an elliptically symmetric variable to one that is spherically symmetric. But unlike the ICA case, there is no orthonormal matrix V that can affect the MI of the spherically symmetric density of x⃗wht. The reason is simple: p(x⃗wht) is isotropic (it is a function only of the vector length ), and thus the density and its marginals are invariant under orthonormal linear transformation:
Since the MI given in equation 2.1 is a function of the joint and marginal densities, we conclude that I(Vx⃗wht) = I(x⃗wht).
3.3 Radial Gaussianization
Given that linear transforms are ineffective in removing dependencies from the spherically symmetric x⃗wht (and hence the original ESD variable x⃗), we need to consider nonlinear mappings. As described previously, the gaussian is the only spherically symmetric density that is also factorial. Thus, given a nongaussian spherically symmetric variable x⃗wht, a natural solution for eliminating dependencies is to map it to a spherical gaussian using a nonlinear function that acts radially, and thus preserves spherical symmetry. We henceforth term such a transform a radial gaussianization.
Specifically, we write the radial marginal distribution of the whitened source variable, r = ||x⃗wht||, in terms of the ESD generating function, f (·),
where β is the normalizing constant that ensures that the density integrates to one. As a special case, the radial marginal distribution of a spherical gaussian density with unit component variance is a chi density with d degrees of freedom:
where Γ(·) is the standard gamma function.
The unique monotonic and differentiable function that transforms a random variable with distribution pr to one with distribution pχ is the composition of the inverse cumulative density function of pχ with the cumulative density function of pr (Casella & Berger, 2001):
We define the RG transformation as4 as
| (3.1) |
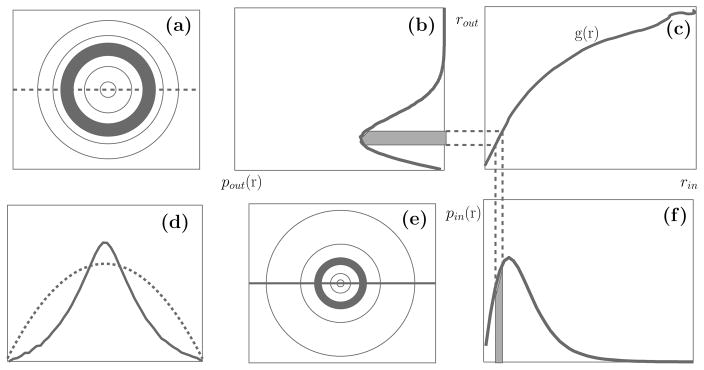
In practice, the radial marginal of the source density may be estimated using a binned histogram. An example of the RG procedure is illustrated in Figure 3, for the case of a spherically symmetric 2D Student’s t variable (see appendix C for a definition).
Figure 3.
Radial gaussianization procedure, illustrated for two-dimensional variables. Joint densities of (a) a spherical gaussian and (b) a nongaussian SSD (multivariate Student’s t). Plotted levels are chosen such that a spherical gaussian has equal-spaced contours. (b,f) Radial marginal densities of the joint gaussian and SSD densities in a,e, respectively. Shaded regions correspond to shaded annuli. (c) Radial map of the RG transform. (d) Log marginal densities of the joint gaussian (dashed line) and SSD (solid line) densities.
3.4 RG for General Signal Models
If x⃗ is not an elliptically symmetric variable, applying RG may not completely eliminate the higher-order dependencies. We can quantify this by reexamining the decomposition of MI in equation 2.2, assuming a whitened source where the second-order terms have been eliminated:
| (3.2) |
We express x⃗ in generalized polar coordinates as x⃗ = r · u⃗, where r = ||x⃗|| and u⃗ is a unit vector. For spherically symmetric densities, p(x⃗) = pr(r)
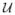 (u⃗), where
(u⃗), where
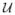 (u⃗) denotes a uniform density on the surface of the d-dimensional unit hypersphere. The first term of the MI expression of equation 3.2 may be written in polar form:
(u⃗) denotes a uniform density on the surface of the d-dimensional unit hypersphere. The first term of the MI expression of equation 3.2 may be written in polar form:
Substituting this back into equation 3.2 gives
| (3.3) |
The RG operation eliminates the first term in equation 3.3. When p(x⃗) is spherically symmetric, the second term is zero since the conditional density of u⃗ given r is
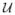 (u⃗). Finally, the last term will also be zero for spherical sources, since RG ensures that the joint density is a spherical gaussian, and thus that the marginals will be gaussian with unit variance.
(u⃗). Finally, the last term will also be zero for spherical sources, since RG ensures that the joint density is a spherical gaussian, and thus that the marginals will be gaussian with unit variance.
For general whitened sources, the second term of equation 3.3 is typically nonzero but is not affected by a radial transform such as RG. On the other hand, the RG operation may actually increase the last term. When the density is close to spherically symmetric, the increase in the last term is likely to be smaller than the reduction resulting from the elimination of the first term, and thus RG may still achieve a reduction in multi-information. But for densities that are close to factorial, RG can result in a net increase in MI (and thus the statistical dependency) in the transformed variables.
Summarizing, ICA and RG are two different procedures for dependency elimination, developed for two complementary generalizations of the gaussian source model, as illustrated in Figure 2. Each can be optimized for, and will be effective in eliminating dependencies of, data drawn from the corresponding source model. A natural question then arises: How relevant is the elliptically symmetric family (and the RG transformation) for real-world signals? In the next section, we examine this question in the context of natural images.
4 Local Image Statistics
The characterization of statistical properties of images is of central importance in solving problems in image processing and in understanding the design and functionality of biological visual systems. The problem has been studied for more than 50 years (see Ruderman, 1996, or Simoncelli & Olshausen, 2001, for reviews). Early analysis, developed in the television engineering community, concentrated on second-order characterization, or gaussian models, of local pixel statistics. Specifically, if one assumes translation invariance (stationary), then the Fourier basis diagonalizes the covariance matrix of pixel intensities, and thus provides principal components for image intensities (see section 2.2). This fact underlies the popularity of frequency domain analysis in early image statistics research.
Starting in the 1980s, researchers began to notice striking nongaussian behaviors of bandpass filter responses (Burt & Adelson, 1981; Field, 1987; Mallat, 1989), and this led to an influential set of results obtained by using newly developed ICA and related methodologies to exploit these behaviors (Olshausen & Field, 1996; van der Schaaf & van Hateren, 1996; Bell & Sejnowski, 1997). These analyses generally produced basis sets containing oriented filters of different sizes with frequency bandwidths of roughly 1 octave. The nature of these results was widely hailed as a confirmation of central hypotheses that had become standard in both scientific and engineering communities. Specifically, the biological vision community had discovered neurons in the primary visual cortex of mammals whose primary response behaviors could be approximated by oriented bandpass filters, and these were hypothesized to have been developed under evolutionary pressure as an efficient means of representing the visual environment (Barlow, 1961; Field, 1987). On the other hand, the computer vision and image processing communities (partly motivated by the biological observations and partly by a desire to capture image features such as object boundaries) advocated the use of banks of oriented bandpass filters for representation and analysis of image data (Granlund, 1978; Koenderink, 1984; Adelson, Simoncelli, & Hingorani, 1987; Mallat, 1989).
Despite the success of ICA methods in providing a fundamental motivation for the use of oriented bandpass filters, there are a number of simple observations that indicate inconsistencies in the interpretation.
From a biological perspective, it seems odd that the analysis produces a solution that seems to bypass the retina and the lateral geniculate nucleus (LGN), two stages of processing that precede visual cortex and exhibit significant nonlinear behaviors in their own responses. Linear approximations of the response properties of these neurons are isotropic (i.e., nonoriented) bandpass filters. If the optimal decomposition for eliminating dependencies is an oriented bandpass filter, why do we not see these in retina or LGN?
The responses of spatially proximal-oriented bandpass filters (including ICA filters) exhibit striking dependencies, in which the variance of one filter response can be predicted from the amplitude of another nearby filter response (Simoncelli, 1997; Buccigrossi & Simoncelli, 1999). This suggests that although the marginal responses are heavy-tailed, the joint responses are not consistent with the factorial source model assumed by ICA.
A related observation is that the marginal distributions of a wide variety of bandpass filters (even a “filter” with randomly selected zero-mean weights) are all highly kurtotic (Baddeley, 1996). This would not be expected for the ICA source model: projecting the local data onto a random direction should result in a density that becomes more gaussian as the neighborhood size increases, in accordance with a generalized version of the central limit theorem (Feller, 1968; see section 4.1.2).
Recent quantitative studies (Bethge, 2006) further show that the oriented bandpass filters obtained through ICA optimization lead to a surprisingly small improvement in terms of reduction in multi-information (MI) relative to second-order decorrelation methods such as PCA.
Taken altogether, these observations suggest that the linearly transformed factorial model underlying ICA is not a good description of local statistics of natural images, and thus the ICA decomposition is perhaps not as ideally suited for image representation as initially believed.
On the other hand, there is substantial empirical evidence (along with associated modeling efforts) indicating that local joint densities of images are approximately elliptically symmetric. This was first noted with regard to pairwise joint statistics of Gabor filters of differing phase (Wegmann & Zetzsche, 1990), and later extended to filters at nearby positions, orientations and scales (Zetzsche & Krieger, 1999; Wainwright & Simoncelli, 2000). As a result, many recent models of local image statistics are members of the elliptically symmetric family (Zetzsche & Krieger, 1999; Huang & Mumford, 1999; Wainwright & Simoncelli, 2000; Hyvärinen et al., 2001; Parra et al., 2001; Srivastava et al., 2002; Sendur & Selesnick, 2002; Portilla et al., 2003; Teh et al., 2003; Gehler & Welling, 2006). This suggests that radial gaussianization may be an appropriate methodology for eliminating statistical dependencies in local image regions. In this section, we examine this hypothesis empirically by first testing the local statistics of bandpass filter responses for ellipticity and then comparing the reduction in MI that is obtained using PCA, ICA, and RG.
4.1 Elliptical Symmetry of Local Image Statistics
In order to examine the elliptical properties of image statistics, we use a calibrated test set of gray-scale images whose pixel values are linear with light intensity (van Hateren & Ruderman, 1998). All images are preprocessed by first taking the log, and then removing the local mean by convolution with a bandpass filter that subtracts from each pixel the mean value over the surrounding block, as in Ruderman and Bialek (1994).
4.1.1 Elliptical Symmetry of Pairwise Pixels Densities
We first examine the statistical properties of pairs of bandpass filter responses with different spatial separations. The two-dimensional densities of such pairs are easy to visualize and can serve as an intuitive reference when we later extend to the pixel blocks.
The top row of Figure 4 shows example contour plots of the joint histograms obtained from a test image. Consistent with previous empirical observations (Wegmann & Zetzsche, 1990; Wainwright & Simoncelli, 2000), the joint densities are nongaussian, with roughly elliptical contours for nearby pairs. For pairs that are distant, both the second-order correlation and the higher-order dependency become weaker, and the corresponding joint histograms show more resemblance to the factorial product of two one-dimensional supergaussian densities, as would be expected for independent random variables.
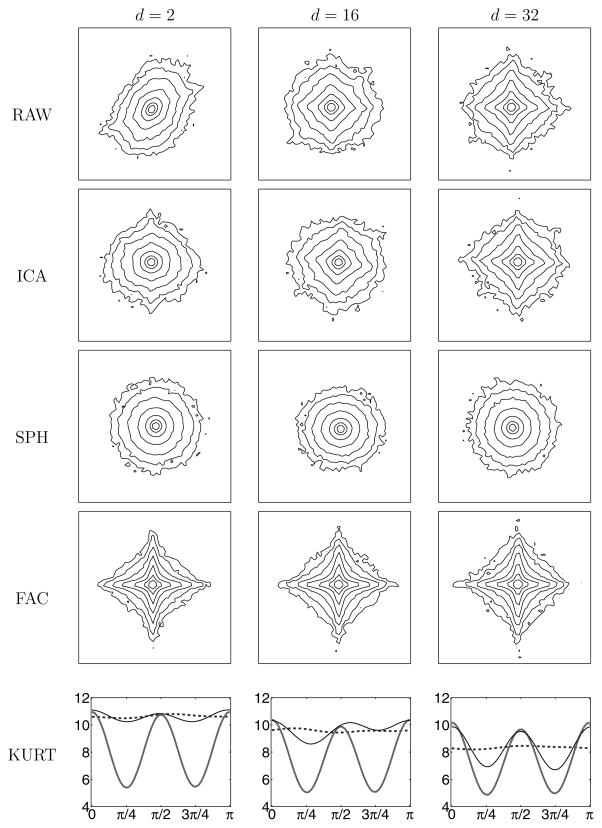
Figure 4.
Joint histograms of pairs of samples from transformed images, at three different spatial separations. Lines indicate level sets of constant probability, chosen such that a gaussian density will have equispaced contours. Data taken from a single test image. RAW: original bandpass filtered image. ICA: data after ICA transformation. SPH: sphericalized synthetic data (randomized directions). FAC: factorialized synthetic data (independently sampled marginal components). KURT: kurtosis of marginal density, as as function of marginal direction, for RAW (thin line), SPH (dashed line), and FAC (thick line) data.
The second row in Figure 4 shows the ICA-transformed pairs. The ICA transform was computed using the RADICAL algorithm (Learned-Miller & Fisher, 2000), an implementation that directly optimizes the MI using a smoothed grid search over a nonparametric estimate of entropy. Note that for adjacent pairs, the transformed density is far from factorial: it has contours that are approximately circular. It is also not a spherical gaussian, which can be seen from the irregular spacing of the contours (plots are drawn such that gaussian contours will be equispaced). Since the spherical gaussian is the only density that is both spherically symmetric and completely factorized (see section 3.1), we can conclude that ICA has not succeeded in removing the higher-order dependencies in the pairs. On the other hand, for pairs that are farther apart, the raw density is closer to factorial and remains relatively unchanged by the ICA transformation.
Next, we compare the distributions of the ICA-transformed pairs with those drawn from synthesized data with related spherically symmetric or complete factorial distributions. Shown in the third row of Figure 4 are histograms of synthetic 2D samples, generated by assigning a random orientation to each ICA-transformed data pair. The resulting samples are (by construction) spherically symmetric, with the same radial marginal as the ICA-transformed pairs. Shown in the fourth row are histograms of synthetic 2D samples, generated by resampling each of the two components independently from the component marginals of the ICA-transformed pairs. The resulting density is factorial (again, by construction), with the same marginal densities as the ICA-transformed pairs. Comparing the histograms in the second row to those in the third and fourth, we see that the densities of the ICA-transformed adjacent pairs are much more similar to the spherically symmetric density than the factorial density. As the separation increases, the ICA-transformed density becomes less circular and starts to resemble the factorial density.
The isotropy of the 2D joint densities shown in Figure 4 can be further illustrated by measuring the sample kurtosis of marginal projections in different directions.5 The last row of Figure 4 shows the kurtosis of the ICA-transformed pairs plotted as a function of marginalization direction. For the spherically symmetric densities of the third row, the marginal sample kurtosis is constant with respect to marginalization direction, apart from fluctuations due to estimation errors from finite sampling. In contrast, the kurtosis of the factorial density shows significantly more variation with marginalization direction.6 The kurtosis of the ICA-transformed adjacent pairs is clearly seen to be better approximated by that of the spherically symmetric density than the factorial density. As the distance increases, the kurtosis of the ICA-transformed pairs fluctuates more and begins to resemble that of the factorial density, indicating that the two components are becoming less dependent.
4.1.2 Elliptical Symmetry of Joint Density of Pixel Blocks
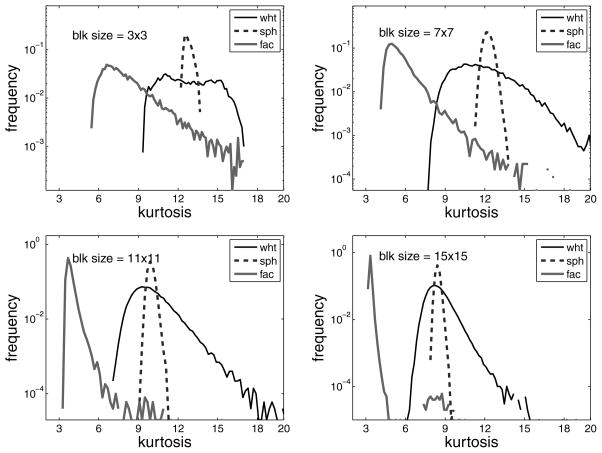
The analysis of the previous section indicates that pairs of spatially proximal bandpass coefficients have approximately spherically symmetric joint densities after whitening. But this does not necessarily guarantee that the densities of blocks of whitened coefficients are also spherically symmetric. There have been relatively few experimental explorations of the joint statistics of coefficient blocks, perhaps because the high dimensionality prohibits the direct visualization that is achievable in the case of pixel pairs. In order to assess spherical symmetry, we examine the distribution of kurtosis values for a large set of random projections.7 If the joint density has spherical symmetry, then the kurtosis (and all other statistics) should be identical for marginals along any direction, and their distribution over random projections should be highly concentrated around the mean value, with variance due to with variability arising only from the computation from finite samples. On the other hand, for a nongaussian factorial density with identical marginals, such higher-order statistics will vary depending on how close a randomly chosen projection direction is to one of the cardinal axes (the independent components). The distribution of kurtosis over random projections in this case will be spread more widely. We can thus use such a distribution of kurtoisis as an indicator of the spherical symmetry of the joint density in the high-dimensional space.
Shown in Figure 5 are distributions of kurtosis of 105 × b2 random projections of ICA-transformed b × b blocks of bandpass-filtered images. In this case, ICA is implemented with the FastICA (Hyvärinen, 1999), which is more efficient and reliable for data of more than a few dimensions. Specifically, we used contrast function g(u) = 1 − exp(−u2), and the optimization was done using the symmetric approach. The factor of b2 in the number of sampled projections compensates for the expected increase in sampling-induced variability that arises as the block size increases. In each plot, the thin curves correspond to the ICA-transformed bandpass filtered pixel blocks. As in the pairwise case, the dashed curves are computed on samples from a synthetic sphericalized data set with radial distribution matching the original data, and the thick curves are computed on a synthetic factorial data set with marginal distributions matching the original data.
Figure 5.
Histograms of kurtosis values for ICA transformed pixel blocks (thin), sphericalized synthetic data (dashed), and factorialized synthetic data (thick). Data are taken from a set of 10 images.
We can use these distributions of kurtosis as an indicator of the spherical symmetry of the underlying joint density. Specifically, the mean of these distributions is the average kurtosis over all marginals and can be taken as a measure of the gaussianity of “typical” projections of the data. The width of the distributions is determined by differences in the kurtosis of the marginal projections along different directions, as well as variability that arises from the estimation of kurtosis from finite samples. This latter component of the variability may be seen directly in the distributions corresponding to the sphericalized data in Figure 5. Since these distributions are spherically symmetric by construction, all variability is due to sampling.
Consider the distributions corresponding to the factorialized data. For small block sizes, the kurtosis varies substantially, ranging from roughly 5 to 16. The large values correspond to marginal directions that are well aligned with one of the cardinal axes. The smaller values correspond to marginal directions that are poorly aligned with the cardinal axes (e.g., the marginal along the direction ), and thus are averaging together the independent marginal variables. These averages tend to be significantly more gaussian than the distributions along the cardinal axes.8 As the block size grows, alignment with the cardinal axes becomes rarer, and the distribution becomes more concentrated toward three (the value one expects for a gaussian).
Now consider the distributions of kurtosis for the ICA-transformed pixel blocks (black dashed curves). For all block sizes, they have a mean that is similar to that of the data from a spherically symmetric joint density, but consistently and substantially larger than that of the data from a factorial density. We also see that the distribution is not quite as concentrated as that of the corresponding spherically symmetric density. Thus, there is some variation in kurtosis that cannot be attributed to sampling, implying that the underlying densities for the pixel blocks are not perfectly spherically symmetric.
4.2 Dependency Reduction with RG
Empirical results in the previous section suggest that local joint densities of bandpass filter responses are closer to elliptical than factorial; thus, RG is likely to be more effective in reducing their statistical dependencies than linear transforms such as PCA and ICA. In this section, we test this assertion directly.
In order to implement RG, we estimate the radial marginal density of the whitened data. From a set of whitened training data {x⃗1, …, x⃗n}, a trapezoidal approximation of Fr, F̂r, is obtained as follows. First, we reorder the training data into {x⃗i1, …, x⃗in}, such that ||x⃗|| ≤ ··· ≤ ||x⃗in||. Then F̂r is computed as
In practice, if n is sufficiently large, the obtained F̂r (r) will be smooth and a good approximation of Fr (r). A nonparametric estimation of Fχ(r), F̂χ(r) can be obtained similarly by generating a set of spherical gaussian samples of the same dimensionality. From F̂χ(r) and F̂r (r), a lookup table can be constructed with proper interpolation, as , to approximate the continuous function g(r). It is also possible, though not necessary, to fit it with piece-wise smooth functions (e.g., splines).
4.2.1 MI Reduction for Pixel Pairs
We begin by comparing the reduction of statistical dependency in pairs using each of the methods described previously. We estimated the MI for x⃗raw, x⃗wht, x⃗ica, and x⃗rg on pairs of bandpass filter responses separated by distances ranging from 1 to 35 samples. Here, the MI was computed using a recent nonparametric method based on the order statistics (Kraskov, Stögbauer,& Grassberger, 2004). This approach belongs to the class of “binless” estimator of entropy and mutual information, which alleviates the strong bias and variance intrinsic to the more traditional binning (i.e., “plug-in”) estimators. It is especially effective in this particular case, where the data dimension is two.
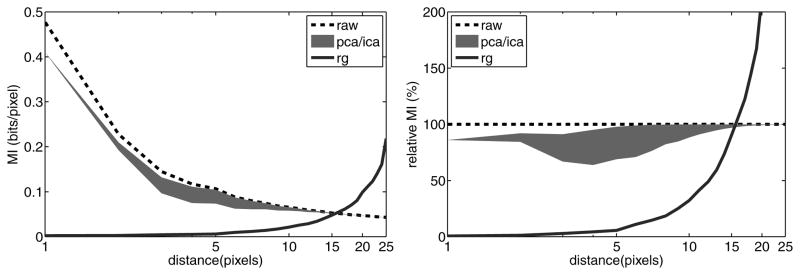
The results, averaged over ten images, are plotted in Figure 6. First, we note that PCA produces a relatively modest reduction in MI: roughly 20% for small separations, decreasing gradually for larger separations. More surprisingly, ICA offers no additional reduction for small separations and a relatively modest improvement for separations of between 12 and 32 samples. This is consistent with the histograms and kurtosis analysis shown in Figure 4, which suggest that the joint density of adjacent pairs has roughly elliptical contours. As such, we should not expect ICA to provide much improvement beyond what is obtained with a whitening step.
Figure 6.
Multi-information for original bandpass filtered pixel pairs (dashed line), compared with PCA (top of gray region), ICA (bottom of gray region) and RG (solid line) transformations. All values are averages over 10 images.
The behavior for distant pairs is also consistent with the results shown in Figure 4. These densities are roughly factorial and thus require no further transformation to reduce MI. So ICA again provides a very small reduction, as is seen in the plots of Figure 6 for separations beyond 32 samples. The behavior for intermediate separations indicates that in the transition from spherically symmetric density to more factorial density, there is a range where ICA can result in a reduction in MI (e.g., middle columns of Figure 4).
In comparison to PCA and ICA, the nonlinear RG transformation achieves an impressive reduction (nearly 100%) in MI for pairs separated by fewer than 16 samples. Beyond that distance, the joint densities are closer to factorial, and RG can actually make the pairs more dependent, as indicated by an increase in MI.
4.2.2 MI Reduction for Pixel Blocks
In the next set of experiments, we generalize our analysis to examine the effects of RG in reducing dependencies within pixel blocks. As with the kurtosis analyses of the previous section, the generalization from pairs to blocks is more difficult computationally. Specifically, direct estimation of the MI of pixel blocks becomes increasingly difficult (and less accurate) as the block size grows. This problem may be partially alleviated by instead evaluating and comparing differences in MI between different transforms (Bethge, 2006). Details are provided in appendix B.
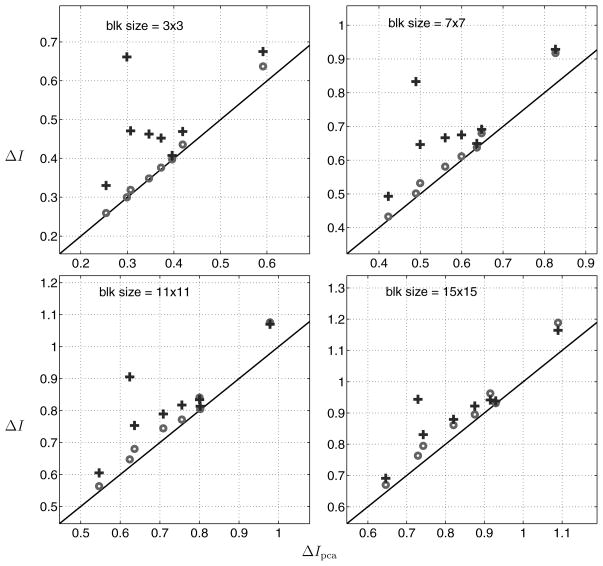
For the sake of comparison, we use ΔIpca = I(x⃗raw) − I(x⃗pca) as a reference value and compare this with ΔIica = I(x⃗raw) − I(x⃗ica) and ΔIrg = I(x⃗raw) − I(x⃗rg). Shown in Figure 7 are scatter plots of ΔIpca versus ΔIica and ΔIrg for various block sizes. Each point corresponds to MI computation over blocks from one of eight bandpass-filtered test images. As previously, the ICA algorithm was implemented with FastICA.
Figure 7.
Comparison of reduction of MI achieved by ICA and RG against that achieved by ICA, for pixel blocks of four different sizes. Each symbol corresponds to a result from one image in our test set. Pluses denote ΔIrg, and circles denote ΔIica.
As shown in Figure 7, for small block sizes (e.g., 3 × 3), RG achieves a significant reduction in MI, whereas ICA shows only a small improvement over PCA. Since PCA-based whitening is usually used as a preprocessing step for ICA, this suggests that the ICA algorithm does not offer much advantage over second-order decorrelation algorithms such as PCA, which may be attributed to the fact that the joint density for local pixel blocks is roughly elliptical. It also suggests that the amount of higher-order dependency in these blocks is significant compared to the second-order correlations measured by the MI reduction of PCA. Similar results have been obtained with a slightly different method of removing the mean values of each block (Bethge, 2006). On the other hand, as the block size increases, the advantage of RG in reducing statistical dependency fades, consistent with the fact that the pairwise densities for coefficients become less dependent as their separation increases, and thus the multidimensional joint density of larger blocks will tend to deviate more from being elliptically symmetric.
5 Relationship to Divisive Normalization
In recent years, a local gain control model, known as divisive normalization (DN), has become popular for modeling biological vision. In DN, responses of a bandpass filter are divided by a Minkowski combination of a cluster of neighboring response amplitudes. This type of model has been used to explain nonlinearities in the responses of mammalian cortical neurons (Heeger, 1992; Geisler & Albrecht, 1992) and nonlinear masking phenomenon in human visual perception (Foley, 1994; Teo & Heeger, 1994; Watson & Solomon, 1997). Empirically, it has been shown that locally dividing bandpass-filtered pixels by local standard deviation can produce approximately gaussian marginal distributions (Ruderman, 1996) and that a weighted DN nonlinearity can reduce statistical dependencies of oriented bandpass filter responses (Simoncelli, 1997; Buccigrossi & Simoncelli, 1999; Schwartz & Simoncelli, 2001; Valerio & Navarro, 2003). Recently, several authors have developed invertible image transformations that incorporate DN (Malo et al., 2000; Malo, Epifanio, Navarro, & Simoncelli, 2006; Gluckman, 2006; Lyu & Simoncelli, 2007). Since DN provides a nonlinear means of reducing dependencies in bandpass representations of images, it is natural to ask how it is related to the RG methodology introduced in this article.
Given decorrelated input variable x⃗ ∈
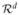 , we define the DN transform as (Simoncelli, 1997):
, we define the DN transform as (Simoncelli, 1997):
where ci and b are the transform parameters.9 When the weights are all identical (ci = c, ∀i), for example, as a result of whitening, DN becomes a radial transform:
| (5.1) |
where
| (5.2) |
with scalars b and c as transform parameters.
In practice, the transform parameters in the DN transform are learned from a set of data samples. Previously this parameter learning problem was formulated to maximize likelihood, where specific marginals were assumed for x⃗dn (Schwartz & Simoncelli, 2001; Wainwright et al., 2002). In this work, we employ an alternative learning scheme that explicitly optimizes the DN parameters to reduce MI. Specifically, we optimize the difference in MI from whitened input data x⃗wht to the DN transformed data x⃗dn:
| (5.3) |
Note that is a constant with regard to the DN parameters, and the Jacobian of DN transform is given as
where r = ||x⃗wht||(see appendix A), and the optimization is reduced to
| (5.4) |
We then use a grid search to find the values of {b, c} that maximize equation 5.4, where the expectation over r is replaced by averaging over training data and the entropy H((x⃗dn)i) is computed using a nonparametric m-spacing estimator (see section B.1).
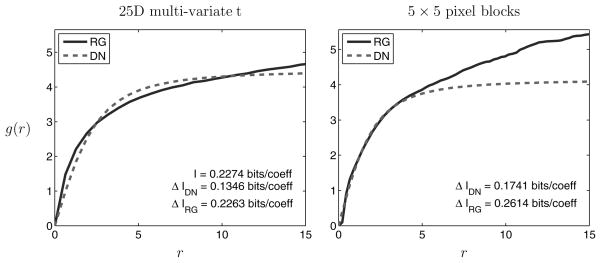
Figure 8 shows two comparisons of RG and optimal DN transformations. The first shows results obtained by optimizing over 105 25-dimensional multivariate Student’s t samples. The multivariate Student’s t density is a member of the elliptically symmetric family, and its MI can be computed in closed form (see appendix C). Note that for relatively small values of r, the DN radial map closely approximates the RG radial transform. But we also see that the DN radial transform saturates at large values, while the RG radial transform continues to increase. Finally, note that DN eliminates a bit more than half of the MI, whereas RG eliminates nearly all of it. The right side of Figure 8 shows a comparison of RG and DN applied to one image in the van Hateren database. Similar to the case of multivariate Student’s t, the DN radial transform approximates the RG radial transform and reduces a substantial fraction of the MI. Nevertheless, it falls significantly short of the performance of the RG transform.
Figure 8.
Comparison of radial transforms corresponding to RG (solid line) and DN (dashed line), each optimized to minimize MI for 105 samples of a 25-dimensional spherical Student’s t density (left), and 5 × 5 pixel blocks taken from one bandpass-filtered test image (right). Average MI reduction is indicated for each transform.
Finally, we note that the functional form of the DN transform suggests that it cannot fully remove the dependencies of spherically symmetric densities. Specifically, the radial transform in RG, g(·), must have as its range the entire half-interval [0, ∞) since the support of the target χ-distribution is [0, ∞). On the other hand, the radial DN transform, expressed in equation 5.2, saturates at a value of for large values of r.
6 Discussion
We have introduced a new form of nonlinear statistically adaptive signal transformation, radial gaussianization (RG), which is designed to remove dependencies in signals drawn from elliptically symmetric densities (ESDs). The RG methodology is complementary to that of ICA, which is effective in removing statistical dependencies for linear transformation of independent sources but ineffective for ESDs. An important aspect of our development of this methodology is the emphasis on source models. The RG transformation may be applied to data from any source, but it is guaranteed to produce independent responses only when the source is elliptically symmetric, and it may actually increase dependencies of certain class of source models.
Several other nonlinear methods for dependency elimination may be found in the literature. In particular, ICA has been generalized to allow nonlinear transformations (Hyvärinen & Pajunen, 1999), and RG may be viewed as a special case of this generalization. On the other hand, kernel PCA (Mika et al., 1999) may be viewed as a nonlinear gaussianization of a signal (although it not usually formulated in this way), followed by a PCA step to remove any remaining dependencies. Although the concepts underlying nonlinear ICA and kernel PCA are quite appealing, success relies on choosing the right nonlinear map or kernel function, which is quite difficult in practice if one does not know the source model. RG, by comparison, is designed for a specific family of source densities, for which it is guaranteed to work. Chen and Gopinath (2000) proposed an iterative scheme that alternates between ICA and marginal gaussianization transformations. Although this method is guaranteed to transform any source density into a spherical gaussian, the overall transformation is a composition of the iterated alternating sequence of linear transforms and marginal nonlinearities and is difficult to interpret due to substantial distortion of the original source space. This would be especially true for the case of elliptically symmetric sources, for which RG provides an efficient one-step procedure.
In the second half of this article, we demonstrated the use of RG on gray-scale natural image data, where we found it highly effective in removing dependencies within local blocks of bandpass filtered images. This dependency reduction greatly surpasses that of ICA, which is only slightly more effective than PCA. These results are complementary to a number of recent observations in the literature regarding statistical properties of images. As mentioned previously, the fact that marginal densities of all local zero-mean filter responses (even random filters) are highly kurtotic (Baddeley, 1996) is consistent with an ESD description. Several authors have noted that spherical symmetry of local image densities arises naturally from local oriented image features that occur with arbitrary phases or angles (Zetzsche & Barth, 1990; Kohonen, 1996; Zetzsche & Krieger, 1999; Parra et al., 2001), and these concepts have been incorporated in some recent approaches for unsupervised learning of local image structures. Specifically, independent subspace analysis (Hyvärinen & Hoyer, 2000), topographical ICA (Hyvärinen et al., 2001), and hierarchical ICA models (Karklin & Lewicki, 2005; Shan, Zhang, & Cottrell, 2007) all assume that image data are generated from linearly transformed densities that are formed by combining clusters of variables whose dependency cannot be further reduced by linear transformation. In all these cases, we expect that the densities of these local clusters are approximately elliptical, in which case the RG framework should be relevant for eliminating the dependencies captured by these generative models. Finally, we note that similar statistical behaviors have been observed in sound signals (Schwartz & Simoncelli, 2001; Turner & Sahani, 2008), and our preliminary investigation indicates that RG is also effective in removing dependencies in those signals (Lyu & Simoncelli, 2009).
A number of extensions of RG are worth considering in the context of image representation. First, in the examples shown here, we have estimated the optimal RG transformation nonparametrically from sample data. It is worth asking whether there are specific subfamilies of ESD for which this nonlinear transformation may be expressed in closed form. Second, we have seen that RG nearly eliminates the multi-information within small blocks, but that performance worsens as the block size increases. This is expected. As noted earlier, distant samples are nearly independent, and thus (since they are marginally nongaussian) are not well described by ESDs. As such, the RG solution does not provide a global solution for removing dependencies from images. One possible solution is to assume that the image density can be partitioned into independent elliptically symmetric subspaces (Hyvärinen & Hoyer, 2000; Wainwright, Simoncelli, & Willsky, 2001). Alternatively, one could try to develop a more flexible model that transitions naturally from the ESD to the ICA model. One natural means of achieving this is to use the local ESD description as a basis for constructing a Markov random field, which can naturally exhibit local elliptical symmetry and (implicitly defined) dependencies that fade with distance (Lyu & Simoncelli, 2009a). And third, since the RG methodology generates responses with much less dependency than the input, it provides an approximate solution to the efficient coding problem in the noise-free case (Barlow, 1961; Dayan & Abbott, 2001; Simoncelli & Olshausen, 2001). A worthwhile avenue for future investigation is to examine how the solution would be affected by the incorporation of sensor or channel noise (Zhaoping, 2006). Although RG is unlikely to remain optimal in the presence of channel noise, we expect that a globally extended RG transform might still be effective for image compression. In previous work, we found that divisively normalized representations can produce improvements in the rate-distortion trade-off (for MSE and in terms of visual quality) compared with their linear counterparts (Lyu & Simoncelli, 2007).
The results presented in this article may also be interpreted in the context of biological sensory systems. RG requires an initial whitening transform, and a natural choice10 results in local center-surround filters. In addition, we’ve shown that the optimal nonlinear radial transformation is similar to the gain control operations that have been used to model the response properties of mammalian visual neurons in retina (Shapley & Enroth-Cugell, 1984), LGN (Mante, Bonin, & Carandini, 2008), and primary visual cortex (Heeger, 1992; Geisler & Albrecht, 1992). Thus, it seems that the RG transformation on images is most readily identified with the functional processing of center-surround cells in the mammalian retina (e.g., the “parasol” cells in macaque monkey). This is also sensible from a normative perspective: the axons of these cells (along with other ganglion cell classes) make up the optic nerve, which is a bottleneck for visual information that is transmitted to the brain and has presumably been under evolutionary pressure to maximize information transmission (Srinivasan, Laughlin, & Dubs, 1982; Atick & Redlich, 1990), and the solution in the noise-free case should generate independent responses. The RG methodology may seem at first inconsistent with this interpretation, since RG outputs are (ideally) zero-mean and gaussian, whereas ganglion cell responses (specifically, firing rates) are positive and typically heavy-tailed. But note that the RG transformation can be followed by a nonlinear marginal operation that serves to rectify and sparsify the responses without altering the dependency reduction.11
Finally, while we have argued that RG is a better methodology for eliminating local dependencies in natural images than ICA and that it provides a normative explanation for both linear and nonlinear aspects of retinal processing, we have lost the best-known benefit arising from ICA (and related sparse coding methods): an explanation for oriented receptive fields found in primary visual cortical neurons (e.g., Olshausen & Field, 1996, 1997; Bell & Sejnowski, 1997; van Hateren & Ruderman, 1998; Hyvärinen & Hoyer, 2000; Hyvärinen, Hurri, & Väyrynen, 2003). It is important to recognize that despite its effectiveness, RG does not eliminate all dependencies from images. For example, an RG transformation based on isotropic filters cannot eliminate local orientation structure in images. Preliminary observations indicate that the statistics of images that have been processed using local RG transformations contain higher-order statistical regularities and that oriented receptive fields can emerge from ICA or sparse coding analyses of these signals.
Supplementary Material
Acknowledgments
This work was supported by the Howard Hughes Medical Institute and was done when S. L. was a postdoctoral fellow at the Center for Neuroscience at New York University. We thank M. Raphan for valuable discussions and an anonymous reviewer for thorough and constructive comments on the submitted manuscript.
Appendix A: Jacobian of Radial Transform
In this appendix, we derive the Jacobian of a radial transform as used in equation 3.1. Denote ; we would like to compute .
Defining , we have
where δij is the Kronecker delta function. Rewriting in matrix form and defining r = ||x⃗||, we have
where Id is a d-dimensional identity matrix. Using the identity det(a Id + bx⃗x⃗T) = ad−1(a + bx⃗T x⃗) (Abadir & Magnus, 2005), we can rewrite the determinant of as
| (A.1) |
For the DN radial transform of equation 5.1, in which g has the form of equation 5.2, a simple substitution of equation A.1 yields equation 5.3.
Appendix B: Computing Differences in Multi-Information
Direct estimation or optimization of multi-information (MI) is problematic for high-dimensional data. In our experiments, we do not need to compute the MI directly, only the reduction of MI that is achieved by each transformation. Therefore, we compute the difference in MI between raw data and transformed data. For an invertible transform φ:
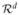 ↦
↦
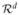 , the change in MI from x⃗ to y⃗ = φ(x⃗) is computed as
, the change in MI from x⃗ to y⃗ = φ(x⃗) is computed as
Therefore, the computation of ΔI can be split into two parts: (1) estimating marginal entropies for the input and transformed variables, H(xi) and H(yi), and (2) computing the expected log Jacobian . We describe these two steps in the following subsections.
B.1 Marginal Entropy Estimation
To estimate the entropy for the 1D marginal densities p(xi) and p(yi), we employed the nonparametric m-spacing entropy estimator (Vasicek, 1976). We briefly describe this algorithm here: a more comprehensive tutorial can be found at Learned-Miller and Fisher (2000). Assume one is given a set of independent and identically distributed data samples (x1, …, xN). Let z1 ≤ ··· ≤ zN be the sorted data values. Next, for integer m, the m-spacing entropy estimator is computed as
where is the digamma function. The m-spacing estimator is strongly consistent, that is, as m → ∞, and m/N → 0, Ĥ(z1, …, zN) → H(z) with probability 1. For our experiments, we set .
B.2 Computing Expected Log Jacobian
For linear transforms, the log Jacobian, , is a constant equal to the log determinant of the transform matrix. Note that when the linear transform is orthonormal, the log Jacobian is zero.
For the nonlinear RG transform, the log Jacobian can be directly computed from the radial transform, g(r), as
where r = ||x⃗|| (see appendix A). Then the expectation over x⃗ of the log Jacobian in this case is computed as
In practice, the differentiation is computed numerically, and the expectation is implemented by averaging over the training data.
Appendix C: Multivariate Student’s t Density
The d-dimensional Student’s t density is the multivariate extension of the Student’s t distribution (Casella & Berger, 2001), and its density is defined as
where α, β, and Σ are model parameters. It can be shown that its multi-information is computed as
where is the digamma function.
Footnotes
Because of this, multi-information is sometimes casually referred to as mutual information.
The quantity DKL(p(x⃗)||
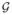 (x⃗)) is known as the negentropy.
(x⃗)) is known as the negentropy.
For our purposes here, we assume M is square and invertible (i.e., the number of basis functions is equal to the dimensionality of the input space), as in Olshausen and Field (1996), Bell and Sejnowski (1997), and van Hateren and Ruderman (1998). A variety of related methods consider the problem of describing signals as a superposition of a small subset of an overcomplete dictionary of basis functions (e.g., Coifman & Wickerhauser, 1992; Mallat & Zhang, 1993; Olshausen & Field, 1997; Chen, Donoho, & Saunders, 1998; Lewicki & Sejnowski, 2000; Donoho & Elad, 2003).
We define kurtosis as the ratio between the fourth-order centered moments and the squared second-order centered moment (i.e., variances): κ(x) = E{(x − E(x))4}/(E{(x −E(x))2})2. With this definition, a gaussian density has kurtosis of 3.
Note that the ICA transformation on pairs results in slightly different marginal statistics depending on the separation d, resulting in slightly different kurtosis behavior.
A more sophisticated hypothesis test of elliptical symmetry using higher-order statistics was proposed in Manzotti, Pérez, and Quiroz (2002), but we have chosen to use the more intuitive approach of comparing kurtosis distributions.
This is expected from an extension of the central limit theorem, which states that random linear combinations of independent random variables tend toward a gaussian (Feller, 1968). It is also the justification for most ICA algorithms, which search for the most nongaussian marginals.
For biological modeling, the DN transform is sometimes defined with squared numerator and denominator: (Schwartz & Simoncelli, 2001). Note that X⃗dn can be mapped to x⃗dn, and vice versa, using a point-wise operation. As MI is not affected by point-wise operations, we may choose either for the analysis of dependency reduction.
The whitening transformation is not unique, but it is common to select the one corresponding to a symmetric matrix transformation, which minimizes the distortion induced by the transformation (Atick & Redlich, 1990).
Indeed, a noise-free formulation of efficient coding dictates that the responses, in addition to being independent, should have marginal distributions that maximize information transmission subject to response constraints. For example, if one assumes a metabolically motivated limit on mean firing rate, then the marginal response distribution should be exponential (Baddeley, 1996; Dayan & Abbott, 2001).
Contributor Information
Siwei Lyu, Email: lsw@cs.albany.edu, Computer Science Department, University at Albany, State University of New York, Albany, NY 12222, U.S.A.
Eero P. Simoncelli, Email: eero@cns.nyu.edu, Howard Hughes Medical Institute, Center for Neural Science, and Courant Institute for Mathematical Sciences, New York University, New York, NY 10003, U.S.A
References
- Abadir KM, Magnus JR. Matrix algebra. Cambridge: Cambridge University Press; 2005. [Google Scholar]
- Adelson EH, Simoncelli EP, Hingorani R. Proc SPIE Visual Communications and Image Processing II. Vol. 845. Bellingham, WA: SPIE; 1987. Orthogonal pyramid transforms for image coding; pp. 50–58. [Google Scholar]
- Andrews DF, Mallows CL. Scale mixtures of normal distributions. Journal of the Royal Statistical Society, Series B (Methodological) 1974;36(1):99–102. [Google Scholar]
- Atick JJ, Redlich AN. Towards a theory of early visual processing. Neural Computation. 1990;2:308–320. [Google Scholar]
- Attneave F. Some informational aspects of visual perception. Psych Rev. 1954;61:183–193. doi: 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
- Baddeley R. Searching for filters with “interesting” output distributions: An uninteresting direction to explore. Network. 1996;7:409–421. doi: 10.1088/0954-898X/7/2/021. [DOI] [PubMed] [Google Scholar]
- Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith WA, editor. Sensory communication. Cambridge, MA: MIT Press; 1961. pp. 217–234. [Google Scholar]
- Bell AJ, Sejnowski TJ. The “independent components” of natural scenes are edge filters. Vision Research. 1997;37(23):3327–3338. doi: 10.1016/s0042-6989(97)00121-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bethge M. Factorial coding of natural images: How effective are linear models in removing higher-order dependencies? J Opt Soc Am A. 2006;23(6):1253–1268. doi: 10.1364/josaa.23.001253. [DOI] [PubMed] [Google Scholar]
- Buccigrossi RW, Simoncelli EP. Image compression via joint statistical characterization in the wavelet domain. IEEE Transactions on Image Processing. 1999;8(12):1688–1701. doi: 10.1109/83.806616. [DOI] [PubMed] [Google Scholar]
- Burt P, Adelson E. The Laplacian pyramid as a compact image code. IEEE Transactions on Communication. 1981;31(4):532–540. [Google Scholar]
- Cardoso JF. High-order contrasts for independent component analysis. Neural Computation. 1999;11(1):157–192. doi: 10.1162/089976699300016863. [DOI] [PubMed] [Google Scholar]
- Cardoso JF. Dependence, correlation and gaussianity in independent component analysis. J Mach Learn Res. 2004;4(7–8):1177–1203. [Google Scholar]
- Casella G, Berger RL. Statistical inference. 2. Pacific Grove, CA: Duxbury Press; 2001. [Google Scholar]
- Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing. 1998;20(1):33–61. [Google Scholar]
- Chen SS, Gopinath RA. Gaussianization. In: Leen TK, Dietterich TG, Tresp V, editors. Advances in neural computation systems. Vol. 13. Cambridge, MA: MIT Press; 2000. pp. 423–429. [Google Scholar]
- Coifman RR, Wickerhauser MV. Entropy-based algorithms for best basis selection. IEEE Trans Info Theory. 1992;38(2):713–718. [Google Scholar]
- Comon P. Independent component analysis, a new concept? Signal Process. 1994;36:387–314. [Google Scholar]
- Cover T, Thomas J. Elements of information theory. 2. Hoboken, NJ: Wiley-Interscience; 2006. [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- Donoho DL, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization. Proc National Academy of Sciences. 2003;100(5):2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang K, Kotz S, Ng K. Symmetric multivariate and related distributions. London: Chapman and Hall; 1990. [Google Scholar]
- Feller W. An introduction to probability theory and its applications. Vol. 1. Hoboken, NJ: Wiley; 1968. [Google Scholar]
- Field DJ. Relations between the statistics of natural images and the response properties of cortical cells. J Opt Soc Am A. 1987;4(12):2379–2394. doi: 10.1364/josaa.4.002379. [DOI] [PubMed] [Google Scholar]
- Foley J. Human luminance pattern-vision mechanisms: Masking experiments require a new model. J Opt Soc Am A. 1994;11(6):1710–1719. doi: 10.1364/josaa.11.001710. [DOI] [PubMed] [Google Scholar]
- Gehler P, Welling M. Products of “edge-perts”. In: Weiss Y, Schölkopf B, Platt J, editors. Advances in Neural Information Processing Systems. Vol. 18. Cambridge, MA: MIT Press; 2006. pp. 419–426. [Google Scholar]
- Geisler WS, Albrecht DG. Cortical neurons: Isolation of contrast gain control. Vision Research. 1992;8:1409–1410. doi: 10.1016/0042-6989(92)90196-p. [DOI] [PubMed] [Google Scholar]
- Gluckman JM. Higher order pyramids: An early vision representation. In: Leonardis A, Bischof H, Prinz A, editors. European Conference on Computer Vision (ECCV) Berlin: Springer-Verlag; 2006. [Google Scholar]
- Granlund GH. In search of a general picture processing operator. Computer Graphics and Image Processing. 1978;8(2):155–173. [Google Scholar]
- Heeger DJ. Normalization of cell responses in cat striate cortex. Visual Neural Science. 1992;9:181–198. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
- Huang J, Mumford D. IEEE International Conference on Computer Vision and Pattern Recognition. New York: IEEE; 1999. Statistics of natural images and models. [Google Scholar]
- Hyvärinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Transactions on Neural Networks. 1999;10(3):626–634. doi: 10.1109/72.761722. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Hoyer P. Emergence of phase- and shift-invariant features by decomposition of natural images into independent feature subspaces. Neural Computation. 2000;12(2):1705–1720. doi: 10.1162/089976600300015312. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Hoyer PO, Inki M. Topographic independent component analysis. Neural Computation. 2001;13:1527–1558. doi: 10.1162/089976601750264992. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Hurri J, Väyrynen J. Bubbles: A unifying framework for low-level statistical properties of natural image sequences. J Opt Soc Am A. 2003;20(7):1237–1252. doi: 10.1364/josaa.20.001237. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Pajunen P. Nonlinear independent component analysis: Existence and uniqueness results. Neural Networks. 1999;12(3):429–439. doi: 10.1016/s0893-6080(98)00140-3. [DOI] [PubMed] [Google Scholar]
- Jolliffe I. Principal component analysis. 2. Berlin: Springer-Verlag; 2002. [Google Scholar]
- Karklin Y, Lewicki MS. A hierarchical Bayesian model for learning non-linear statistical regularities in non-stationary natural signals. Neural Computation. 2005;17(2):397–423. doi: 10.1162/0899766053011474. [DOI] [PubMed] [Google Scholar]
- Kingman JFC. Random walks with spherical symmetry. Acta Math. 1963;109(9):11–53. [Google Scholar]
- Koenderink JJ. The structure of images. Biological Cybernetics. 1984;50:363–370. doi: 10.1007/BF00336961. [DOI] [PubMed] [Google Scholar]
- Kohonen T. Emergence of invariant-feature detectors in the adaptive-subspace self-organizing map. Biological Cybernetics. 1996;75(5):281–291. [Google Scholar]
- Kraskov A, Stögbauer H, Grassberger P. Estimating mutual information. Phys Rev E. 2004;69(6):66–82. doi: 10.1103/PhysRevE.69.066138. [DOI] [PubMed] [Google Scholar]
- Learned-Miller EG, Fisher JW. ICA using spacings estimates of entropy. Journal of Machine Learning Research. 2000;4(1):1271–1295. [Google Scholar]
- Lewicki MS. Efficient coding of natural sounds. Nature Neuroscience. 2002;5(4):356–363. doi: 10.1038/nn831. [DOI] [PubMed] [Google Scholar]
- Lewicki MS, Sejnowski TJ. Learning overcomplete representations. Neural Computation. 2000;12:337–365. doi: 10.1162/089976600300015826. [DOI] [PubMed] [Google Scholar]
- Lyu S, Simoncelli EP. Proceedings of the IS&T/SPIE 19th Annual Symposium of Electronic Imaging. Bellingham, WA: SPIE; 2007. Statistically and perceptually motivated nonlinear image representation. [Google Scholar]
- Lyu S, Simoncelli EP. Nonlinear extraction of “independent components” of elliptically symmetric densities using radial Gaussianization (Tech. Rep. TR2008-911) New York: Courant Institute of Mathematical Sciences, New York University; 2008. [Google Scholar]
- Lyu S, Simoncelli EP. Modeling multiscale subbands of photographic images with fields of gaussian scale mixtures. IEEE Trans Patt Analysis and Machine Intelligence. 2009a;31(4):693–706. doi: 10.1109/TPAMI.2008.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu S, Simoncelli EP. Reducing statistical dependencies in natural signals using radial gaussianization. In: Koller D, Schuurman D, Bengio Y, Bottou L, editors. Advances in neural information processing systems. Vol. 21. Cambridge, MA: MIT Press; 2009b. [PMC free article] [PubMed] [Google Scholar]
- Mallat SG. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans Patt Analysis and Machine Intelligence. 1989;11:674–693. [Google Scholar]
- Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries. IEEE Trans Signal Proc. 1993;41(12):3397–3415. [Google Scholar]
- Malo J, Epifanio I, Navarro R, Simoncelli EP. Nonlinear image representation for efficient perceptual coding. IEEE Trans Image Processing. 2006;15(1):68–80. doi: 10.1109/tip.2005.860325. [DOI] [PubMed] [Google Scholar]
- Malo J, Navarro R, Epifanio I, Ferri F, Artigas J. Proc SPR +SSPR. Berlin: Springer-Verlag; 2000. Non-linear invertible representation for joint statistical and perceptual feature decorrelation; pp. 658–667. [Google Scholar]
- Mante V, Bonin V, Carandini M. Functional mechanisms shaping lateral geniculate responses to artificial and natural stimuli. Neuron. 2008;58:625–638. doi: 10.1016/j.neuron.2008.03.011. [DOI] [PubMed] [Google Scholar]
- Manzotti A, Pérez FJ, Quiroz AJ. A statistic for testing the null hypothesis of elliptical symmetry. Journal of Multivariate Analysis. 2002;81(2):274–285. [Google Scholar]
- Mika S, Schölkopf B, Smola AJ, Müller K-R, Scholz M, Rätsch G. Kernel PCA and de-noising in feature spaces. In: Kearns MS, Solla SA, Cohn DA, editors. Advances in neural information processing systems. Vol. 11. Cambridge, MA: MIT Press; 1999. [Google Scholar]
- Nash D, Klamkin MS. A spherical characterization of the normal distribution. Journal of Multivariate Analysis. 1976;55:56–158. [Google Scholar]
- Nolan JP. Stable distributions—Models for heavy tailed data. Boston: Birkhäuser; 2009. In progress, Chapter 1 online at http://academic2.american.edu/~jpnolan. [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vision Research. 1997;37:3311–3325. doi: 10.1016/s0042-6989(97)00169-7. [DOI] [PubMed] [Google Scholar]
- Parra L, Spence C, Sajda P. Higher-order statistical properties arising from the non-stationarity of natural signals. In: Leen TK, Dietterich TG, Tresp V, editors. Advances in neural information processing systems. Vol. 13. Cambridge, MA: MIT Press; 2001. pp. 786–792. [Google Scholar]
- Portilla J, Strela V, Wainwright MJ, Simoncelli EP. Image denoising using a scale mixture of gaussians in the wavelet domain. IEEE Trans Image Processing. 2003;12(11):1338–1351. doi: 10.1109/TIP.2003.818640. [DOI] [PubMed] [Google Scholar]
- Ruderman DL. The statistics of natural images. Network: Computation in Neural Systems. 1996;5:517–548. [Google Scholar]
- Ruderman DL, Bialek W. Statistics of natural images: Scaling in the woods. Phys Rev Letters. 1994;73(6):814–817. doi: 10.1103/PhysRevLett.73.814. [DOI] [PubMed] [Google Scholar]
- Schwartz O, Simoncelli EP. Natural signal statistics and sensory gain control. Nature Neuroscience. 2001;4(8):819–825. doi: 10.1038/90526. [DOI] [PubMed] [Google Scholar]
- Sendur L, Selesnick IW. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans Signal Proc. 2002;50(11):2744–2756. [Google Scholar]
- Shan H, Zhang L, Cottrell GW. Recursive ICA. In: Schölkopf B, Platt J, Hoffman T, editors. Advances in neural information processing systems. Vol. 19. Cambridge, MA: MIT Press; 2007. pp. 1273–1280. [Google Scholar]
- Shapley R, Enroth-Cugell C. Visual adaptation and retinal gain control. Progress in Retinal Research. 1984;3:263–346. [Google Scholar]
- Simoncelli EP. Proc 31st Asilomar Conf on Signals, Systems and Computers. Vol. 1. Washington, DC: IEEE Computer Society; 1997. Statistical models for images: Compression, restoration and synthesis; pp. 673–678. [Google Scholar]
- Simoncelli EP, Olshausen B. Natural image statistics and neural representation. Annual Review of Neuroscience. 2001;24:1193–1216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- Srinivasan MV, Laughlin SB, Dubs A. Predictive coding: A fresh view of inhibition in the retina. J R Soc Lond B. 1982;216:427–459. doi: 10.1098/rspb.1982.0085. [DOI] [PubMed] [Google Scholar]
- Srivastava A, Liu X, Grenander U. Universal analytical forms for modeling image probability. IEEE Trans Patt Anal Mach Intell. 2002;24(9):1200–1214. [Google Scholar]
- Studeny M, Vejnarova J. The multiinformation function as a tool for measuring stochastic dependence. In: Jordan MI, editor. Learning in graphical models. Dordrecht: Kluwer; 1998. pp. 261–297. [Google Scholar]
- Teh Y, Welling M, Osindero S. Energy-based models for sparse overcomplete representations. Journal of Machine Learning Research. 2003;4:1235–1260. [Google Scholar]
- Teo PC, Heeger DJ. IEEE Intl Conf on Image Proc. New York: IEEE; 1994. Perceptual image distortion; pp. 982–986. [Google Scholar]
- Turner R, Sahani M. Modeling natural sounds with modulation cascade processes. In: Platt J, Koller D, Singer Y, Roweis S, editors. Advances in neural information processing systems. Vol. 20. Cambridge, MA: MIT Press; 2008. [Google Scholar]
- Valerio R, Navarro R. Optimal coding through divisive normalization models of V1 neurons. Network: Computation in Neural Systems. 2003;14:579–593. [PubMed] [Google Scholar]
- van der Schaaf A, van Hateren JH. Modelling the power spectra of natural images: Statistics and information. Vision Research. 1996;28(17):2759–2770. doi: 10.1016/0042-6989(96)00002-8. [DOI] [PubMed] [Google Scholar]
- van Hateren JH, Ruderman DL. Independent component analysis of natural image sequences yields spatio-temporal filters similar to simple cells in primary visual cortex. Proc R Soc Lond B. 1998;265:2315–2320. doi: 10.1098/rspb.1998.0577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasicek O. A test for normality based on sample entropy. Journal of the Royal Statistical Society, Series B. 1976;38(1):54–59. [Google Scholar]
- Wainwright MJ, Schwartz O, Simoncelli EP. Natural image statistics and divisive normalization: Modeling nonlinearity and adaptation in cortical neurons. In: Rao R, Olshausen B, Lewicki M, editors. Probabilistic models of the brain: Perception and neural function. Cambridge, MA: MIT Press; 2002. pp. 203–222. [Google Scholar]
- Wainwright MJ, Simoncelli EP. Scale mixtures of gaussians and the statistics of natural images. In: Solla SA, Leen TK, Müller KR, editors. Advances in neural information processing systems. Vol. 12. Cambridge, MA: MIT Press; 2000. pp. 855–861. [Google Scholar]
- Wainwright MJ, Simoncelli EP, Willsky AS. Random cascades on wavelet trees and their use in modeling and analyzing natural imagery. Applied and Computational Harmonic Analysis. 2001;11(1):89–123. [Google Scholar]
- Watson A, Solomon J. A model of visual contrast gain control and pattern masking. J Opt Soc Amer A. 1997;14:2379–2391. doi: 10.1364/josaa.14.002379. [DOI] [PubMed] [Google Scholar]
- Wegmann B, Zetzsche C. Proc Visual Comm and Image Processing. Vol. 1360. Bellingham, WA: SPIE; 1990. Statistical dependence between orientation filter outputs used in an human vision based image code; pp. 909–922. [Google Scholar]
- Yao K. A representation theorem and its applications to spherically-invariant random processes. IEEE Trans on Information Theory. 1973;19(9):600–608. [Google Scholar]
- Zetzsche C, Barth E. Fundamental limits of linear filters in the visual processing of two-dimensional signals. Vision Research. 1990;30:1111–1117. doi: 10.1016/0042-6989(90)90120-a. [DOI] [PubMed] [Google Scholar]
- Zetzsche C, Krieger G. The atoms of vision: Cartesian or polar? J Opt Soc Am A. 1999;16(7):1554–1565. [Google Scholar]
- Zetzsche C, Schönecker W. Orientation selective filters lead to entropy reduction in the processing of natural images. Perception. 1987;16:229. [Google Scholar]
- Zetzsche C, Wegmann B, Barth E. Intl Symposium, Society for Information Display. Vol. 24. Campbell, CA: Society for Information Display; 1993. Nonlinear aspects of primary vision: Entropy reduction beyond decorrelation; pp. 933–936. [Google Scholar]
- Zhaoping L. Theoretical understanding of the early visual processes by data compression and data selection. Network: Computation in Neural Systems. 2006;17(4):301–334. doi: 10.1080/09548980600931995. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.