The protein folding network indicates that the ultrafast folding mutant of villin headpiece subdomain has a deeper folding funnel

Abstract

Protein folding is a dynamic process with continuous transitions among different conformations. In this work, the dynamics in the protein folding network of villin headpiece subdomain (HP35) has been investigated based on multiple reversible folding trajectories of HP35 and its ultrafast folding mutant where sub-angstrom folding was achieved. The four folding states were clearly separated on the network, validating the classification of the states. Examination of the eight conformers with different formation of the individual helices revealed high plasticity of the three helices in all the four states. A consistent feature between the wild type and mutant protein is the dominant conformer 111 (all three helices formed) in the folded state and conformers 111 and 011 (helices II and III formed) in the major intermediate state, indicating the critical role of helices II and III in the folding mechanism. When compared to the wild type, the folding landscape of the ultrafast folding mutant exhibited a deeper folding funnel towards the folded state. The very beginning of the folding (0–10 ns) was very similar for both protein variants but it soon diverged and displayed different folding pathways. Although going through the major intermediate state is the dominant pathway for both, it was also observed that some folding went through the minor intermediate state for the mutant. The intriguing difference resulting from the mutation at two residues in helix III has been carefully analyzed and discussed in details.

INTRODUCTION

Protein folding is a dynamic process consisting of continuous making and breaking of native contacts, both locally and globally. To monitor protein folding process, various experimental techniques have been developed or applied,^{1, 2} including fluorescence, Forster resonance energy transfer, infrared spectroscopy, Raman spectroscopy, circular dichroism, nuclear magnetic resonance, and hydrogen-deuterium exchange. In a recent work by Takahashi and co-workers, time-resolved small-angle x-ray scattering was applied to the folding study of barnase³ in which two burst phase intermediates were found, one with non-native cis-proline isomer and the other with native trans proline isomer. The relatively extended conformation of these two intermediates suggested that only the N-terminal helix was formed at the early stage and the rest of the protein folded in a much slower phase. In another study, fluorescence correlation spectroscopy was applied to the folding study of cytochrome c.⁴ It was found that the presence of arginine favored the more compact structure in the unfolded state, and the formation of the collapsed state took ∼30 μs. In addition to the folding experiments, theoretical studies play a complementary role in understanding the protein folding dynamics. In a recent work by Shakhnovich and co-workers, the folding of a three-strand β-sheet WW domain was examined by all atom Monte Carlo simulation with a knowledge-based potential.⁵ Two major folding pathways were observed with different orders in the formation of the two hairpins. In another work by Pande, an analytical kinetic model was built in order to better interpret folding simulations.⁶ It was found that the native state serves as kinetic hub which connects various non-native states.

Villin headpiece subdomain (HP35) has been a model protein to study folding mechanism. Its unique three-helix architecture packed in a small size (35 residues) has attracted wide attention from both experimentalists and theoreticians,^{1, 7} including recent work by Shaw and co-workers.⁸ The atomic structure has been determined at high resolution, and an ultrafast folding mutant was designed and validated. In our previous theoretical works, we conducted all-atom folding simulations on HP35 wild type and mutant and achieved successful folding in both cases (the lowest C_α RMSD < 0.5 Å).⁹ Based on the simulations, we proposed a two-stage folding mechanism where the conformations with the folded helix II/III segment constitute the primary intermediate state. In a more recent work,¹⁰ we further illustrated the roughness of the folding landscape with a network of conformational clusters, consistent with the folding funnel hypothesis.¹¹

Traditionally, due to the limitation of one-dimensional profiles, such as root mean square deviation (RMSD) and two-dimensional maps, it has been challenging to present the roughness of the folding landscape. The situation has been changed in recent years with the development or application of new techniques. In 2002, Krivov and Karplus proposed a disconnectivity graph with a tree representation of the populated conformations from simulation.¹² Protein folding network was first visualized in the work of Duan and Kollman¹² and more recently explored by Caflisch and co-workers,¹³ Pande and co-workers,¹⁴ Schulten and co-workers,¹⁵ and Xiao and co-workers.¹⁶ With the application of these new techniques, protein folding mechanism can be examined at finer details.

In our recent work, we analyzed the folding network of the HP35 wild type based on five long trajectories by molecular dynamics simulation.¹⁰ In this work, we generated additional five reversible folding trajectories (10 μs each) of HP35 mutant by molecular dynamics simulation. The five trajectories of each of the HP35 variants were combined for the network analyses. By constructing the folding networks at different time frames, including 0–10 ns, 10–100 ns, 0.1–1.0 μs, 1.0–10 μs, and the full 10 μs, we attempted to study the dynamics of the networks and the time evolution during the folding. The folding of HP35 was compared at each of the time frames for the two variants. Furthermore, the events leading to the first folding in each individual trajectory were also examined.

METHODS

The simulations were conducted with the “sander” program in the AMBER simulation package.¹⁷ From previous ab initio folding simulations (1 μs for each trajectory),⁹ five trajectories for the HP35 mutant were selected to continue to 10 μs from the previous endpoints of 1 μs. As in the previous simulations, the all-atom point-charge force field AMBER FF03 was chosen to represent the protein,¹⁸ and the combined generalized-Born¹⁹ and surface area model was chosen to mimic the solvation effect (IGB = 5 and surface tension = 0.005 kcal/mol/Ų). The temperature was set to 300 K and was controlled by applying Berendsen's thermostat²⁰ with a coupling time constant of 2.0 ps. Ionic strength was set to 0.2 M. The cutoff for both general non-bonded interaction and generalized-Born pairwise summation was set to 12 Å. SHAKE was applied for the bond constraint.²¹ The time step was set to 2 fs. Slow-varying terms were evaluated every four steps. The coordinates were saved every 10 ps. The simulations were run on a Linux computer cluster and each simulation trajectory occupied a single node with 8 cores. It took about 15 min to complete each 1 ns runs and the total computer time for each 10 μs simulation would be around 104 days if uninterrupted.

The snapshots were classified into four folding states based on the C_α- RMSDs of segments A and B (R_A and R_B), where segment A is the helices I/II segment (residues 2–20) and segment B is the helices II/III segment (residues 13–31). Consistent with the results from our earlier studies, the two-dimensional folding landscape can be divided into four distinct regions (see Fig. 1 in supplementary material²²): the folded region N (bottom left, R_A < 2.0 Å and R_B < 2.0 Å), the unfolded region U (top right, R_A > 2.0 Å and R_B > 2.7 Å), the major intermediate region I₁ (bottom right, R_A > 2.0 Å and R_B < 2.7 Å), and the minor intermediate region I₂ (top left, R_A < 2.0 Å and R_B > 2.0 Å).

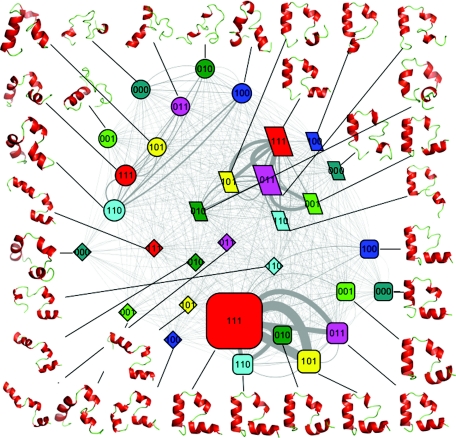
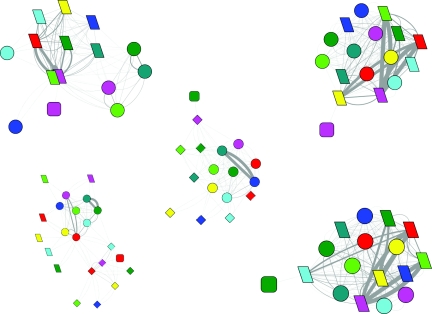
Figure 1.

The folding network of HP35 mutant. Node shape is based on the folding states (round rectangle for the native state, ellipse for the unfolded state, parallelogram for the intermediate 1 state, and diamond for the intermediate 2 state); node color is based on the eight conformers (red for conformer 111, cyan for conformer 110, yellow for conformer 101, purple for conformer 011, blue for conformer 100, dark green for conformer 010, green for conformer 001, and dark cyan for conformer 000); node size is based on population of each substate; Edge line width is based on the number of transitions between each pair of substates.

The snapshots were also classified into eight conformers based on the formation of the individual helices. For helix I, the conformer code is “1” if five out of the seven residues (residues 3–9) are in helical dihedral zone and those five residues are consecutive, otherwise the code is “0”. For helix II, the conformer code is “1” if four out of the six residues (residues 14–19) are in helical dihedral zone and those four residues are consecutive, otherwise the code is “0”. For helix III, the conformer code is “1” if seven out of the ten residues (residues 22–31) are in helical dihedral zone and those seven residues are consecutive, otherwise the code is “0.” Helical dihedral zone is defined as Φ within −57° ± 40° and ψ within −47° ± 40°. There are a total of eight conformers from different combination of the three individual helices, namely, 111, 110, 101, 011, 100, 010, 001, and 000. Thus, there are eight possible sub-states within each of four folding state, resulting in a total of 32 substates.

Comprehensive network analyses were conducted for both HP35 variants based on all five trajectories combined. Each of the 32 substates was a node of the network. The edges of the networks were represented by the transitions among the substates. The change from one substate to another between neighboring snapshots was counted as one transition. Nodes with at least one direct transition were linked together. A network software CYTOSCAPE was used to visualize the network.²³ An organic layout was chosen to present the network. The network nodes were colored by the conformers and assigned to different shapes based on the folding state.

Hierarchical clustering was conducted on the combined trajectories for both HP35 varaints. Two snapshots were considered as neighbors when their pairwise C_α-RMSD was below 2.0 Å. One residue from each terminus was excluded in the clustering due to high flexibility. Within each cluster, the snapshot with the most neighbors was identified as the center of the cluster. The process was iterated to identify other clusters from the remaining snapshots. The choice of the cutoff value for clustering is important. In our previous work,⁹ we experimented with 1.5 Å, 2.0 Å, 2.5 Å, and 3.0 Å and concluded that 2.0 Å was the most appropriate cutoff for this protein based on the optimal balance between the separation of clusters and the number of clusters. Therefore, we chose 2.0 Å as the cutoff for the clustering in this work. The clustering results were used to choose the criteria for the classification of helix conformers. We experimented using the cluster center as a representative of all members in a cluster, but eventually decided to classify conformer for each snapshot directly.

RESULTS

Five trajectories of each of the HP35 variants⁹ were selected from the 1 μs molecular dynamics simulations to continue to 10 μs at 300 K. Multiple folding events were observed in all ten trajectories. Network analyses were conducted on the merged trajectories for both HP35 variants. The overall protein folding landscape revealed by the folding network of the wild type HP35 from the five trajectories have been reported in our recent publication.¹⁰ In this work, we describe the time evolution of the folding networks and comparison between the two variants.

The reversible folding of HP35 mutant, as measured in terms of C_α-RMSD (residues 2–34, excluding the terminal residues 1 and 35, and relative to the x-ray structure of HP35 with the PDB code 1YRF), is illustrated in Fig. 2 of the supplementary material.²² As we can see from the global C_α-RMSD profiles, the native state was reached several times in all five trajectories of the mutant, similar to that of the wild type. In trajectory MT4, the native state was reached during 1.0–4.2 μs, 5.8–6.5 μs, and 7.7–10.0 μs. In trajectory MT5, the native state was reached during 0.2–0.4 μs, 2.4–7.1 μs, and 8.0–10.0 μs. In trajectory MT6, the native state was reached during 1.0–3.7 μs and 4.8–10.0 μs. In trajectory MT9, the native state was reached during 1.8–4.0 μs. In trajectory MTA, the native state was reached during 0.2–0.9 μs, 2.0–3.5 μs, 4.9–5.5 μs, and 6.6–10.0 μs. With the exception of trajectory MT9, the native state was predominant within the duration of the simulation and remained stable at the end of the 10.0 μs simulations. This was in clear contrast with the simulations of the HP35 wild type where the native state had much lower population.

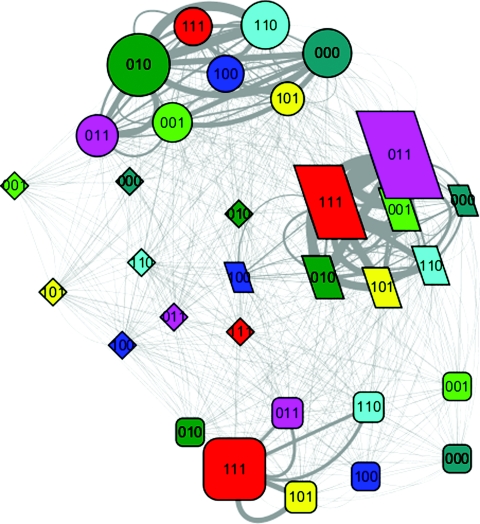
Figure 2.

The folding network of HP35 wild type. (Refer to Fig. 1 for detailed legend.)

In order to dissect the folding mechanism of HP35 and understand the contribution of the mutation to the folding, we conducted analyses based on the folding network. To construct the network, we divided the conformational space into four folding states (U, F, I_1, and I₂) and eight helix conformers (111, 000, 001, 010, 100, 011, 101, and 110). For definition of the folding states and helix conformers, refer to Sec. 2. For each of the 32 substates, we calculated the average potential energy and the number of native hydrogen bonds. A simplified folding landscape was constructed based on these two reaction coordinates which demonstrated the progressive increase of native hydrogen bonds and decrease of potential energy during the folding process (see Fig. 3 in supplementary material).²² The folding network was visualized by the network analysis software CYTOSCAPE. Here, we describe the network analyses in details.

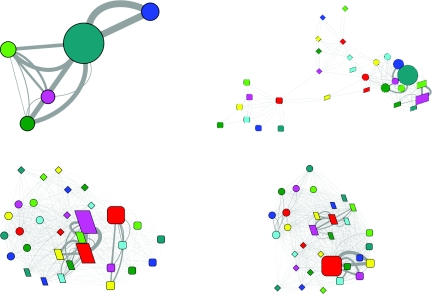
Figure 3.

The evolution of the folding network for HP35 mutant. Upper left, 0–10 ns; upper right, 10–100 ns; lower left, 0.1–1.0 μs; lower right, 1.0–10.0 μs. (Refer to Fig. 1 for detailed legend.)

Comparison of the folding network

First, we compared the population of the folding states, conformers, and the three helices from the two sets of simulations (see Table 1 in supplementary material).²² The population of the native state was 51.9% for the mutant, while only 13.9% for the wild type. Not surprisingly, this was accompanied by the significant decrease of the population of the other three states for the mutant, down from 47.9% to 33.8% for the I₁ state, 37.6% to 14.0% for the U state, and 0.6% to 0.2% for the I₂ state. As for the eight conformers, the population of the most populated conformer 111 is 54.7% for the mutant, more than twice that of the wild type (26.0%). This is accompanied by the decrease of population for most other conformers except for conformer 101 which increased from 7.1% to 9.7%. The second most populated conformer remained to be conformer 011, although the population decreased from 22.1% to 16.6%. It should be noted that the conformers with 0–1 helices, namely, conformers 000, 001, 010, and 100, all had low population ranging from 1.6% to 3.7% in the mutant simulation. In contrast, the combined population for those conformers was 34.0% for the wild type. When the three helices were examined independently, a significant increase of population for all three helices was observed in the mutant, from 47.6% to 75.1% for helix I, from 73.4% to 82.2% for helix II, and from 63.5% to 84.7% for helix III. The implication of the population shift will be discussed later.

To construct the folding network, each of the four folding states was further divided into eight sub-states according to the conformer assignment. These 32 sub-states formed the nodes of the network, and the transitions between any pair of sub-states formed the edges of the network. The folding state and conformer are illustrated by node shape and node color, respectively. The population of the sub-states is indicated by the node size, and the frequency of the transition between sub-states is indicated by edge line width. The folding networks for the HP35 mutant and wild type are shown in Figs. 12, respectively.

The overall topologies of the two networks are similar. The unfolded state and native state are clustered at the two ends, while the two intermediate states reside in the middle with good separation between them. Within the native state, the ranking for the top four populated sub-states is the same for both (see Table 2 in supplementary material),²² in the order of conformer 111, 101, 011, and 110. However, every one of those four sub-states has much higher population in the network of the mutant. For example, the population of sub-state 111 is 39.5% for the mutant and 9.8% for the wild type. Within the major intermediate state, the ranking for three of the top four populated sub-states is the same for both, with conformer 011, 111, and 001 ranked at 1, 2, and 4, respectively. Similarly, the population for all those three sub-states is lower for the mutant, with the top ranked sub-state 011 decreased from 16.7% to 12.3%. A notable difference is the change of the no. 3 sub-state from conformer 010 for the wild type (4.5%) to 101 for the mutant (3.2%). Since the minor intermediate state had low population for both cases, we did not observe significant difference in the sub-state population. The major difference resided in the unfolded state, not only the total population was significantly lower for the mutant, but the ranking of the top four sub-states were also different. It was sub-states 010 (9.9%), 000 (6.1%), 110 (5.9%), and 011 (4.2%) for the wild type and 110 (3.8%), 111 (3.3%), 100 (2.0%), and 010 (1.3%) for the mutant.

Next, we examined the conformational transitions (see Tables 3 and 4 in supplementary material).²² Not surprisingly, the ranking of the intra-state transitions followed the ranking of the population of the states. The top inter-state transition is between I₁ and F state, with ∼35% increase for the mutant. This is followed by the transition between I₁ and U state, with ∼50% increase for the mutant. The major difference resided in the next two inter-state transitions. The transition between I₂ and U state decreased more than 90% for the mutant, while the transition between I₂ and F state increased ∼2.5 fold for the mutant.

We then further examined the sub-state transitions. Again, the top ranked intra-state transitions were almost always between the top two populated sub-states. Slight deviation was observed for the unfolded state where the top transition was between no. 1 and no. 3 for both wild type and mutant. To be more specific, it was between the sub-states 111 and 101 for the F state, 111 and 011 for the I₁ state, and 111 and 110 for the I₂ state. As for the U state, it was between sub-states 110 and 010 for the wild type and 110 and 100 for the mutant. On the other hand, the inter-state transition showed almost no similarity between the wild type and mutant. For the mutant, conformer 111 consistently appeared as the top sub-state in the transitions between I₁ and F state, I₁ and U state, and I₂ and U state. In contrast, conformer 111 never showed up as the top sub-state in any of those three inter-state transitions for the wild type.

Evolution of the folding network

The above-described networks were constructed based on the full length trajectories which reflected a quasi-equilibrium state. To further dissect the folding process, we divided the trajectories into four representative time frames, namely, 0–10 ns, 10–100 ns, 0.1–1.0 μs, and 1.0–10 μs and investigated the evolution of the folding network (Fig. 3 for the mutant and Fig. 4 for the wild type). Similar features were observed in the first time frame for both HP35 variants, with exclusive sampling of the unfolded state and dominant presence of sub-state 000. The three sub-states with one helix formation were all sampled. The sub-state 100 only had transition with sub-state 000. In contrast, sub-states 010 and 001 also had transition with each other and with a two helix sub-state 011. A noticeable difference is the higher transition between sub-states 001 and 011 for the mutant.

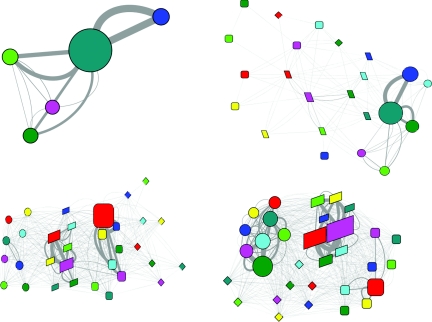
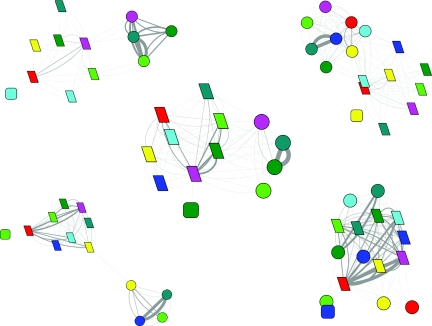
Figure 4.

The evolution of the folding network for HP35 wild type. Upper left, 0–10 ns; upper right, 10–100 ns; lower left, 0.1–1.0 μs; lower right, 1.0–10.0 μs. (Refer to Fig. 1 for detailed legend.)

In the second time frame, the network started to diverge. A common feature was the appearance of the native state, although the unfolded state still dominated. The network topology was quite different for the two HP35 variants. In the network of the mutant, the native state was isolated from the other states with sub-state 111 as the only connection with the two intermediate states. Although the unfolded state had direct transitions with many different sub-states in the two intermediate states, the productive transitions seemed to be from sub-state 111 in the unfolded state to the sub-states 111 and 101 in the I₁ state and 011 in the I₂ state. In the network of the wild type, however, the native state connected to the intermediate states through and with many different conformers. The unfolded state connected only to the I₁ state with no clear preference on the conformers. As for the transition from the I₁ state to the F state, the preferred conformers at the I₁ state seemed to be 011 and 111. The I₂ state was not significantly populated in this time frame for the wild type.

In the third time frame, the two variants continue to show difference in the network topology. In the network of the mutant, the native state was relatively separated from the other three states. The preferred inter-state transitions were mediated solely by the conformer 111, either between the U state and the I₁ state or between the I₁ state and the F state (data not shown). In the network of the wild type, the four states were clearly arranged from left to right, suggesting the folding from the U state to the I₁ state and then to the F state, plus additional transitions between the F state and the I₂ state. The most frequent transitions between the I₁ state and the F state were among conformers 011 and 111 at both states with preference to the transitions between the same conformers (data not shown). Again, no significant preference was observed for the transitions between the U state and the I₁ state.

In the final time frame, the most prominent difference was the population of the states. The native state was the dominant state for the mutant while it was ranked no. 3 after the I₁ state and the U state for the wild type. For both HP35 variants, significant inter-state transitions were observed between the same conformer (either 111 or 011) at the I₁ state and the F state (data not shown), with much higher frequency for the mutant.

The initial folding events

In yet another attempt to further dissect the folding mechanism, we examined the very first folding events in the ten individual trajectories (Figs. 56). The pathways leading to the first folding events were quite diverse for the five trajectories of the mutant, three of which went through the major intermediate state and the other two went through the minor intermediate state. For the three trajectories that went through the I₁ state, no I₂ state was observed. The final inter-state conformational transitions were from conformers 011 to 011, 101 to 011, and 110 to 010 in the three trajectories. For the two trajectories that went through the I₂ state, I₁ state was only observed in one of them. The final inter-state conformational transitions were from conformers 011 to 010 and 011 to 111 in the two trajectories.

Figure 5.

Network illustration of events leading to the first folding events in the five individual trajectories of HP35 mutant. Refer to Fig. 1 for detailed legend. For clarity, node size is set to uniform in this figure.

Figure 6.

Network illustration of events leading to the first folding events in the five individual trajectories of HP35 wild type. Refer to Fig. 1 for detailed legend. For clarity, node size is set to uniform in this figure.

In contrast, the pathways leading to the first folding were very consistent for the five trajectories of the wild type, all of which went through the major intermediate state and there was no observation of the minor intermediate state. Prior to the folding, four of the I₁ sub-states were 111, and the other one was 011. The major difference among the five trajectories was the first conformers in the native state which were all different, including 101, 110, 100, 001, and 010.

DISCUSSION

Based on the observations described in Sec. 3, here we attempt to dissect the folding mechanism of HP35, with an emphasis on the nontrivial contribution from the mutation. Ideally, both HP35 variants should have a dominant native state. However, due to the limited number of trajectories (five each for the wild type and mutant), the observed relative population of different states will not be accurate. In addition, there are errors in the existing force fields. Nevertheless, the qualitative increase of the population of the native state for the mutant is encouraging and provided an opportunity to reveal the contribution of the mutation to the folding.

The mutation in helix III not only increased the population of the well-formed helix III, but also significantly enhanced the formation of the other two helices. More specifically, conformers with at least two well-formed helices became much more populated and conformer 111 became dominant. When the intra-state population distribution was compared, the most significant change was in the unfolded state, where the most populated conformers changed from 010 and 000 for the wild type to 110 and 111 for the mutant. The deeper traps with little helical content in the unfolded state had significantly negative effect on the folding of HP35. Within the other three states, the relative population of the conformer 111 was also significantly higher for the mutant. The dominance of the conformer 111 in turn lowered the energy barrier and facilitated the transition from the unfolded state to the major intermediate state, from the major intermediate state to the native state, and even from the minor intermediate state to the native state. Thus, the overall mutational effect was an enhanced folding rate and increased stability of the native state, in other words, an improved folding funnel towards the native state.

The improved folding funnel was also demonstrated by the state transition. For the unfolded state, the ratio of intra-state versus inter-state transition was three times higher for the wild type, and a large portion of the inter-state transition was towards the unproductive I₂ state (∼38%), while it was mostly towards the I₁ state (∼97%) for the mutant. For the major intermediate state, the preference of transition to the native state rather than going back to the unfolded state was similar for both HP35 variants (3:1). However, the preference of transition out of the state versus within the state was much higher for the mutant (1:3) than the wild type (1:7). Although the population of the minor intermediate state was small for both HP35 variants, the much higher preference of transition to the native state rather than going back to the unfolded state (5:1 for the mutant and 1:7 for the wild type) also had significant contribution to the enhanced folding rate. In addition, the ratio of intra-state versus inter-state transition was lower for the mutant (2.5:1) compared to the wild type (4:1), which means it had higher preference to leave the state. For the native state, the ratio of intra-state versus inter-state transition was 40:1 for the mutant and 16:1 for the wild type, indicating much higher stability of the native state for the mutant. For those transitions out of the native state and towards the I₁ and I₂ state, the ratio was 22:1 for the mutant and 41:1 for the wild type. More transition towards the I₂ state for the mutant was not negative since I₂ state had high preference towards transition back to the native state. Overall, the transition properties indicated that the folding funnel was reshaped to have shallower traps in the unfolded and intermediate states and deeper minimum in the native state for the mutant. In addition, the unproductive I₂ state for the wild type became productive for the mutant, also constituting a major change of the folding landscape.

The difference on the folding landscape can also be seen from the evolution of the folding network. In the second time frame, the population of the I₁ state was notably higher for the mutant, owing to the enhanced transition propensity from U state to I₁ state. The sole conformer 111 at the F state connecting the intermediate states for the mutant was due to the deeper global minima compared with the wild type. In the third time frame, we can see the significant accumulation of the I₁ and F state and diminishing of the U state for both HP35 variants. However, due to the shallower global minima and deeper traps in the I₁ and U state for the wild type, a significant portion shifted back to the I₁ state and some even back to the U state. On the other hand, the continued accumulation of the F state and diminishing of other states for the mutant was due to the improved folding landscape.

The network of events leading to the first folding further demonstrated the change of folding landscape. For the wild type, all five folding events were mediated by the I₁ state while the I₂ state did not even show up on those networks. It was a totally different scenario for the mutant, where two of the five folding events were mediated by the I₂ state in addition to the other three folding events that were mediated by the I₁ state. The rerouting of the folding pathway by two point mutations in helix III is rather intriguing.

In fact, both I₁ and I₂ states have been proposed as the intermediate state for the folding of HP35 wild type from experimental folding studies. Recent works by Gai and co-workers demonstrated the important role of the turn linking helices II and III,²⁴ suggesting I₁ as the intermediate state. In the work by Kiefhaber and co-workers,²⁵ however, the I₂ states was proposed as the intermediate state. The detection of an intermediate state has also been claimed in the recent works by Tycko and co-workers²⁶ and Eaton and co-workers.²⁷ It should be noted that various perturbations have been applied in those experimental folding studies. Our current theoretical work suggests that HP35 is very sensitive to small perturbation, whether by mutating residues, adding fluorescence probe, or changing the environment. We strongly propose that similar experimental work be performed on the HP35 mutant so that we can have a clearer picture of the folding landscape of HP35.

CONCLUSIONS

We conducted folding network analysis on the folding of HP35 wild type and mutant. From the intra-state and inter-state conformational transitions, the folding mechanism can be implied. The mutation in helix III not only stabilized the targeted helix but also made other two helices more stable, which led to the dominant conformer 111 for the mutant. This dominant conformer as well as the conformer 011 facilitated the transitions from the U state to the I₁ state and from the I₁ state to the F state. In addition, it also made the F state more accessible by the I₂ state, which was an off-pathway intermediate for the wild type. In summary, the folding network analysis can provide novel insights into the understanding of folding mechanism.