Multicellular Model for Intercellular Synchronization in Circadian Neural Networks

Abstract

We developed a multicellular model characterized by a high degree of heterogeneity to investigate possible mechanisms that underlie circadian network synchronization and rhythmicity in the suprachiasmatic nucleus (SCN). We populated a two-dimensional grid with 400 model neurons coupled via γ-aminobutyric acid (GABA) and vasoactive intestinal polypeptide (VIP) neurotransmitters through a putative Ca²⁺ mediated signaling cascade to investigate their roles in gene expression and electrical firing activity of cell populations. As observed experimentally, our model predicted that GABA would affect the amplitude of circadian oscillations but not synchrony among individual oscillators. Our model recapitulated experimental findings of decreased synchrony and average periods, loss of rhythmicity, and reduced circadian amplitudes as VIP signaling was eliminated. In addition, simulated increases of VIP reduced periodicity and synchrony. We therefore postulated a physiological range of VIP within which the system is able to produce sustained and synchronized oscillations. Our model recapitulated experimental findings of diminished amplitudes and periodicity with decreasing intracellular Ca²⁺ concentrations, suggesting that such behavior could be due to simultaneous decrease of individual oscillation amplitudes and population synchrony. Simulated increases in Cl⁻ levels resulted in increased Cl⁻ influx into the cytosol, a decrease of inhibitory postsynaptic currents, and ultimately a shift of GABA-elicited responses from inhibitory to excitatory. The simultaneous reduction of IPSCs and increase in membrane resting potential produced GABA dose-dependent increases in firing rates across the population, as has been observed experimentally. By integrating circadian gene regulation and electrophysiology with intracellular and intercellular signaling, we were able to develop the first (to our knowledge) multicellular model that allows the effects of clock genes, electrical firing, Ca²⁺, GABA, and VIP on circadian system behavior to be predicted.

Introduction

In mammals, most physiological and behavioral events are subject to well-controlled daily oscillations. These rhythms are generated by an internal, self-sustained oscillator located in the hypothalamic suprachiasmatic nucleus (SCN). The SCN consists of a broad range of neural subgroups that are differentiated according to their neuropeptide content (1), afferent (2) and efferent (3) connections with other regions of the brain, and oscillatory behavior (4,5). Circadian rhythmicity is ensured not only by autonomous intracellular mechanisms within individual cells (6) but also by intercellular communication that coordinates these functionally and structurally distinct cell types across the SCN (7,8).

A critical element of the circadian clock is postulated to involve intracellular signaling mechanisms instigated by cytosolic Ca⁺² (9). Calcium is a second messenger that affects not only core-clock transcriptional mechanisms but also the electrophysiological properties of the circadian system. Cytosolic calcium has been demonstrated to activate Ca²⁺/calmodulin dependent kinases, which in turn phosphorylate the cAMP-response-element binding (CREB) protein, ultimately leading to Per1 gene induction (9). Decreased Ca²⁺concentrations have been shown to abolish daily Per1 mRNA oscillations in SCN slices (10).

Vasoactive intestinal polypeptide (VIP) is a critical neuropeptide that is involved in the generation and synchronization of circadian rhythms (11). VIP is synthesized primarily in the ventrolateral SCN by ∼10–20% of the 20,000 SCN neurons (10% in mouse (4)), whereas the VIP receptor VPAC2 is expressed by 60% of the neurons across the SCN (12). Mice lacking VIP (13) or VPAC2 (14) have been reported to express multiple circadian rhythms or single rhythms with greatly reduced periods and lower-amplitude oscillations than wild-type mice (11,15). Although the 70% of wild-type SCN neurons that fire in a circadian pattern display similar periods and phases, only 30% of VIP and VPAC2 mutant neurons produce daily oscillations, and they display a significantly broader range of periods (11).

The most abundant neurotransmitter, which originates primarily within the component neurons of the SCN itself, is γ-aminobutyric acid (GABA) (1,4,16). GABA interacts with GABA_A and GABA_B receptors, producing primarily inhibitory responses through membrane hyperpolarization that effectively shunts transmembrane voltage shifts. Recent studies, however, suggest that GABA can also act as an excitatory neurotransmitter in the SCN (17). Simultaneous multichannel recordings from the dorsal and ventral regions of the SCN demonstrated inhibitory effects of GABA within the ventral part at all phases of the circadian cycle (18). Within the dorsal SCN, GABA elicited excitatory responses during late day/early night, and switched back to the usual inhibitory effect during the early/mid circadian day. Such variability in GABA-elicited responses has been attributed to changes in the transmembrane chloride gradient, which determines the direction of current flow and hence the inhibitory or excitatory nature of the response (19,20). Another point of controversy concerns the role played by GABA in synchronizing the SCN network. Although one study showed that daily application of exogenous GABA synchronized the firing rhythms of dispersed SCN neurons (21), in another study it was reported that GABA blockade had no effect on synchronization and was not required for the expression of a coherent signal within SCN slices (22).

Mathematical models of multicellular circadian systems include those that simulate the core oscillator and intercellular coupling mechanisms (23,24). Single-cell oscillator models range from simple limit cycle oscillators (25) to detailed descriptions of interconnected transcriptional and translational feedback loops (26,27). Most previous studies of cell-to-cell communication focused on VIP (23,28) or GABA (29) as the coupling neurotransmitter. The underlying topology in these models included locally connected (23,24,30), mean-field (31), random (24), or small-world (32) networks. Recently, a Hodgkin-Huxley model of SCN neurons was developed to reproduce electrophysiological behavior on a millisecond timescale (33). Another study of particular interest involved a limit cycle oscillator coupled with a leaky integrate-and-fire model (34). This model demonstrated the importance of the bidirectional relationship between the molecular clock and the membrane potential for establishing synchronous circadian signals across the population. Although the results were conceptually appealing, this study did not include detailed descriptions of the molecular clock and the signaling mechanisms that are putatively involved in mediating robust circadian behavior.

In an effort to discover important mechanisms that underlie network synchronization and circadian dynamics, we developed a multicellular SCN population model that is heterogeneous with respect to uncoupled rhythmic behavior, single-cell periodicity, neurotransmitter release, and intercellular coupling. Our model integrates the electrophysiological properties of SCN neurons to obtain daily fluctuations in the firing rate, and also contains descriptions of clock gene transcriptions and the intracellular signaling mechanisms that are responsible for cell-to-cell communication. Our objective was to evaluate the role of various intracellular signaling events and SCN neurotransmitters (VIP and GABA) with respect to their effects on synchronicity and circadian behavior. We further investigated variations in GABA-elicited responses and their effects on system behavior as a function of the cytosolic Cl⁻ level.

Materials and Methods

The SCN population model consists of four fundamental components: a core-clock gene regulatory model, a firing-rate code model of neuronal electrical activity, a cell-to-cell signaling model, and a model of the connection topology between cells. Details about the components, capabilities, and limitations of the model are provided in the Supporting Material.

Computational studies and data analysis

The multicellular model was formulated within MATLAB (The MathWorks, Natick, MA). Each model neuron across the 20 × 20 network grid was characterized by 21 differential equations (ODEs). Two ODEs described cytosolic calcium oscillations; three ODEs described oscillations in VIP, GABA, and phosphorylated CREB concentrations (for details, see Vasalou and Henson (35)); and 16 ODEs described molecular events within the core-clock oscillator (for details, see Leloup and Goldbeter (36)). We modified the equation accounting for GABAergic transmission from our previous single-cell study (35), in which release of the neurotransmitter was modeled as a function of VIP, to obtain a more realistic expression for GABA release as a function of the firing rate (see Supporting Material). The multicellular formulation was characterized by an increased number of model parameters, many of which were obtained from the previously published core-clock gene regulatory model (36) or directly obtained from the literature (35), whereas the remaining parameters were fitted to reproduce experimentally observed behavior (23,35). A small number of parameter values were tuned from our previous study (35) to produce firing rate and Per mRNA oscillations within an experimentally observed range (Table S1). In our previous analyses (35) we found that despite the large number of parameters, the structure of the underlying model played a critical role in producing the desired model behavior, such that an improperly structured model was not tunable.

Random perturbations in the basal Per transcription rate (ν_sp0) with a 6% standard deviation (SD) around its nominal value were introduced in each neuron to create an uncoupled population in which ∼25% of the model neurons were intrinsic oscillators and the remaining neurons did not sustain circadian rhythmicity. The Bmal1 transcription rate (ν_sB), and the Bmal1 mRNA degradation rate (ν_mB) were randomly perturbed with a 1% SD around their nominal values to achieve a distribution of periods among the intrinsic oscillators with their uncoupled periods ranging between 21 and 26 h, as observed experimentally (11). Random perturbations in molecular parameters underlying circadian rhythmicity generated cell-to-cell variability, thereby introducing an element of randomness into our deterministic model. Previous studies that compared predictions of deterministic and stochastic circadian models showed that both model types yield similar results provided that the numbers of molecules involved remain sufficiently large (i.e., on the order of hundreds) (37,38). We obtained the initial cell states from our previously published study on single-cell circadian oscillations (35), and set the initial condition for the ODE accounting for GABA oscillations at 0.01 nM.

We formulated the resulting multicellular model within MATLAB and solved it using the differential-algebraic equation solver ode23 with a 6 min time step to ensure accurate solutions with a reasonable computational cost. Cell-to-cell couplings mediated by VIP-, GABA-, and Ca²⁺-instigated signaling were introduced at 150 h (V_β, V_MK, and GABA_i^f were zeroed for t < 150 h). We allowed each simulation to run for an additional 250 h (≥10 oscillation cycles) after the introduction of intercellular communication to obtain sufficient results to assess synchronicity and circadian behavior. For all simulations, we conducted 10 independent runs and subsequently computed the average and SD at each time point to generate the results.

To evaluate the degree of phase synchronicity, we used the synchronization index (SI) (39). The SI is a measure that quantifies the ability of the system to produce a coherent signal by comparing the instantaneous phase angle of each oscillator relative with a reference cycle. We computed the SI from the Per mRNA concentration of each neuron in the 400 cell ensemble at the end of each oscillation cycle as follows:

$$SI=\left|\frac{1}{N}{e}^{i\vartheta j}\right|,$$ (1)

where N is the number of cells and θ_j is the phase of the jth cell with respect to a reference cycle computed as the population average. The phase θ_j was computed as the difference between the time of peak in the Per mRNA rhythm of the j^th neuron and the peak of the mean Per mRNA of the entire population divided by the average period of the population and multiplied by 2π to convert to radians.

We evaluated circadian robustness by determining changes in the mean amplitudes of the Per mRNA and firing rate oscillations, which we computed by averaging the amplitudes (peak-to-trough) of individual rhythmic cells across the network after introducing various perturbations. Such perturbations included changes in cytosolic Ca²⁺ levels, VIP and GABA concentrations binding to the cell surface, and Cl⁻ transmembrane gradients across the cell membrane. To change the effective Ca²⁺ concentration affecting cell electrophysiology and gene regulation, we scaled the output of the equation responsible for the circadian evolution of intracellular calcium (35) by multiplying with a scaling factor ranging from 0.1 to 1.5. Hence, mean levels of calcium were varied from −90% to 150% of their nominal values. We changed VIP levels by including an additive term in the VIP concentration (γ_i) that binds on the membrane of individual cells (Eq. S1). Hence, VIP concentrations were increased by up to 200% of their nominal values. We performed simulations of incrementally decreasing GABA concentrations by imposing step reductions in the mean GABA levels binding to the cell membrane (Eq. S4), gradually eliminating the effects of GABAergic signaling. We then implemented incremental increases of the GABA concentration binding to the cell surface by including an additive term in the GABA concentration equation (Eq. S4), introducing up to 100 nM additional GABA. Other simulations involved variations in the mean intracellular chloride concentration (as mean Cl⁻ levels were increased from 15 mM to ∼65 mM) implemented by including an additive term in the mathematical expression of cytosolic Cl⁻ oscillations (35).

Results

Circadian dynamics of the model population

We placed an ensemble of 400 model neurons on a 20 × 20 grid to investigate the ability of the heterogeneous population to self-synchronize and produce coherent rhythms in the absence of environmental timing cues. Highly phase-synchronized rhythms in Per mRNA concentrations and firing rates were observed despite the lack of a photic driving signal, in similarity to experimental data (40) (Fig. 1, A and B). Firing-rate oscillations exhibited larger-amplitude variations in comparison with Per mRNA profiles across the coupled population. Within the first 4 days, the SI rapidly increased and then slowly approached an asymptotic value of ∼0.93 (Fig. 1 C). The kinetics of synchronization and the predicted SI value obtained at the end of the simulation were in agreement with data collected from SCN slices, from which an SI value of 0.90 was calculated (32). The synchronized population at the end of 10 cycles had an average period of 23.3 h, whereas the distribution of periods among the individual oscillators had an SD of 0.22 h (Fig. 1 D, upper panel). The uncoupled population (for t < 150 h) was comprised of 75% nonrhythmic cells and 25% intrinsic oscillators. The computed average period across the uncoupled pacemakers was 23.0 h and the SD was 0.65 h (Fig. 1 D, bottom panel). These model predictions are consistent with previous experimental work that showed a period decrease due to elimination of cell-to-cell couplings (11,13,43).

Figure 1.

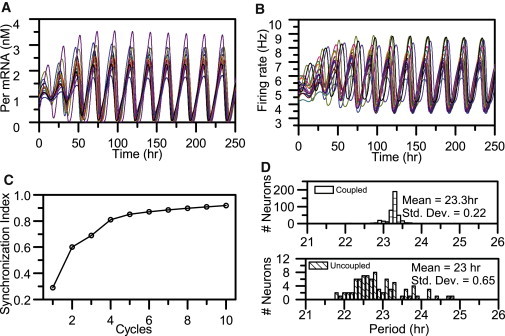
Synchronization dynamics of neurons under environmental conditions of constant darkness. Rhythmic Per mRNA (A) and neural firing frequency (B) profiles of 15 randomly selected circadian neurons. (C) A high degree of synchrony (SI = 0.93) was obtained after four oscillation cycles. (D) The distribution of periods is shown at the 10th cycle for all cells in coupled populations (top panel) and for intrinsic oscillators in uncoupled populations (bottom panel).

Effect of intracellular calcium concentration on circadian dynamics

We varied the intracellular calcium concentration to investigate its effects on synchronization behavior and circadian dynamics under environmental conditions of constant darkness. We found that increasing the intracellular Ca²⁺ concentration up to 150% enhanced the coordination of single oscillators within the model system, as SI values computed at the end of 10 cycle simulations monotonically increased with higher cytosolic Ca²⁺ levels. Using 10 independent runs for each Ca²⁺ concentration, we obtained comparatively small SDs in the synchronization measure after Ca²⁺ reached its nominal value (denoted as 0% Ca_in change in Fig. 2 A). Incrementally increasing intracellular calcium levels produced increased mean Per mRNA and neural firing rate amplitudes across the population (Fig. 2, B–D). By contrast, computed SI values began to decrease once the intracellular Ca²⁺ concentration was increased beyond 150% (not shown). These model predictions can be compared with experimental data on SCN explants, which show abolished mean Per mRNA rhythms, averaged over the SCN population, as a function of increasing concentrations of Ca²⁺ buffer (10). Hence, our model suggests that elimination of circadian rhythmicity of SCN explants in low Ca²⁺ may be attributable to simultaneous reductions in population synchrony and oscillation amplitudes of individual cells as intracellular Ca²⁺ is gradually depleted.

Figure 2.

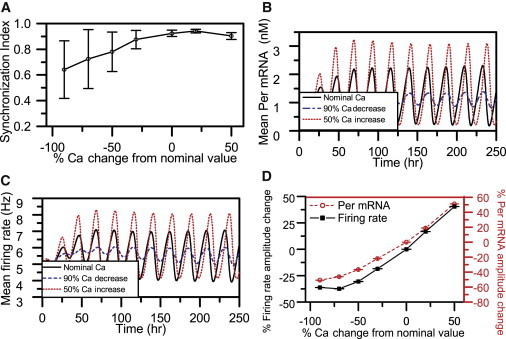
Circadian behavior of the SCN population as a function of intracellular Ca⁺² levels. For each calcium concentration, the mean (circle) and SD (error bars) were computed from 10 independent runs. (A) The SI at the 10th cycle versus % changes in cytosolic Ca²⁺ concentration. Circadian profiles of Per mRNA (B) and neural firing rates (C) averaged over the entire population are shown for nominal calcium concentrations (solid line), 90% decreased intracellular Ca²⁺ (dashed line), and 50% increased cytosolic Ca²⁺ (dotted line) compared with the nominal. (D) Average Per mRNA (dashed line) and firing-rate (solid line) amplitudes as a function of the cytosolic calcium concentration.

Cytosolic Ca²⁺ levels also affected the average period of the model system and the SD of individual neuron periods across the network. Increasing cytosolic Ca²⁺ concentrations produced longer periods of the core oscillator, reaching a maximum of 24.1 h for a 50% Ca²⁺ increase (Fig. S2). These model trends qualitatively agree with experimental studies that demonstrated shorter periods with decreasing cytosolic Ca²⁺ concentrations (10). A more quantitative comparison cannot be made at this time because the necessary experimental data are currently unavailable. We also computed the SDs of the period distribution across the network for each simulation. When these SDs were averaged across 10 independent runs, lower calcium concentrations produced a larger period variability than higher Ca²⁺ levels (Fig. S2). These model predictions require further experimental validation.

Effect of VIP signaling on circadian dynamics

We varied the amount of VIP binding on the membrane surface of our 400 model neurons to investigate the effects of the VIP signaling pathway on system synchronicity and behavior in constant darkness. Initially, we zeroed the VIP signal responsible for the GABA oscillations and Per mRNA activation (35) to mimic experimental work on Vip−/− neurons (11,15). Complete VIP blockade resulted in substantially reduced system synchronicity, as SI values of 0.11 ± 0.05 across 10 independent runs were obtained. Because Per gene expression is the final target of the VIP signaling cascade, elimination of VIP resulted in decreased mean Per mRNA amplitudes by 67%, consistent with the literature (44) (Fig. S3 A). Similarly, mean firing rate amplitudes showed 62% reductions due to VIP loss, in agreement with experiments (45,46) (Fig. S3 B). Such low-amplitude oscillations are due to large populations of nonrhythmic cells, as nearly 75% of the neurons failed to exhibit sustained rhythmicity after VIP was eliminated. The model predictions are in agreement with findings that show loss of rhythmicity in the majority of cells and reduced synchrony within the SCN upon the loss of VIP signaling (11,15).

Additional simulations involved the incremental increase of VIP binding to the cell surface. To our knowledge, experimental data on constitutive VIP administration throughout 24-h periods are not currently available. Across 10 independent runs implemented for each VIP concentration, we observed a dose-dependent increase in mean circadian amplitudes of firing frequency and Per mRNA as increasing VIP concentrations were applied (Fig. 3 A and Fig. S3, C–D). Our simulations further showed an incremental decrease in system synchronicity with increasing VIP concentrations (Fig. 3 B). SI values continued to decrease with a slower rate once the VIP concentration was increased by >200%. The model therefore suggests a threshold in VIP concentration above which population coordination is observed to decrease in a dose-dependent manner. The average period of the model system also monotonically decreased, from 23.3 to 22.8 h, due to increased VIP levels (Fig. 3 C). These model predictions are consistent with experimental work on VPAC2 receptor overexpression in transgenic mice that showed shorter circadian periods (0.6-h reductions compared with wild-type mice) in constant darkness (47).

Figure 3.

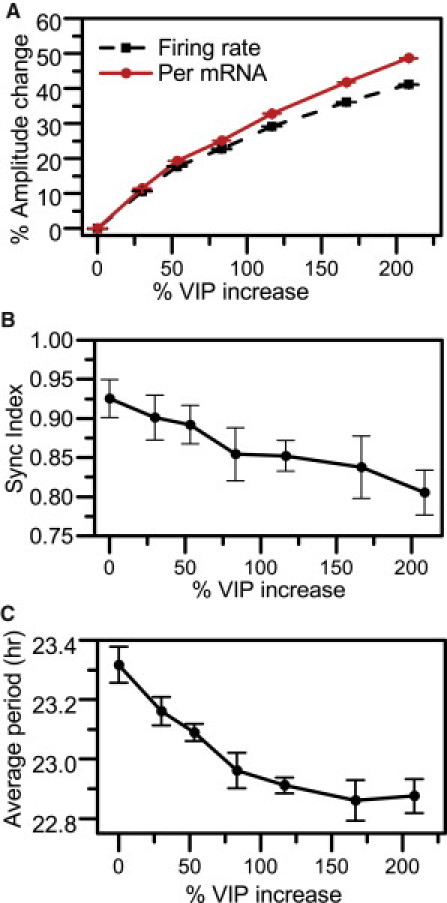
Effect of varying VIP concentration on SCN population behavior. For each VIP concentration, the mean (circle) and SD (error bars) were computed from 10 independent runs. (A) Mean Per mRNA (solid line) and firing-frequency (dashed line) amplitudes as a function of VIP application. (B) The SI at the 10th cycle of our simulations versus % increases in VIP concentration. (C) Average period of the model network versus % increases in VIP.

Effect of GABA signaling on circadian dynamics

We varied the amount of GABA binding to the cell surface to investigate the effects of inhibitory postsynaptic currents (IPSCs) on system synchronization and circadian behavior. Our first tests involved simulations of incrementally decreasing GABA concentrations. Across 10 independent runs implemented for each GABA concentration, system synchrony and average period were observed to remain constant regardless of GABA levels across the network. As GABA was gradually decreased, values of the SI measure and the average period remained at ∼0.9 and 23.3 h, respectively. By contrast, the mean circadian amplitudes of firing rate and Per mRNA were shown to be dependent on the GABA level. These predictions are in agreement with experimental findings that although endogenous GABA controls circadian amplitudes, it is not required for synchrony among SCN neurons (22). We evaluated the effect of GABA reduction on the electrophysiological properties of our system during the subjective day and night by computing the percent changes in firing frequency peak and trough versus these values at nominal GABA levels. As GABA was depleted from the model, the mean neural firing rate showed a dose-dependent increase during both the subjective day and night (Fig. 4 A), in agreement with the literature (48). Such a response can be attributed to IPSC reductions caused by the depletion of GABA across the population, further affecting neuron excitability. The mean Per mRNA amplitude also exhibited a concentration-dependent effect, as GABA reduction led to increased mean Per mRNA levels during the subjective day and had a minimal effect during the subjective night (Fig. 4 B), in similarity to experimental data (22).

Figure 4.

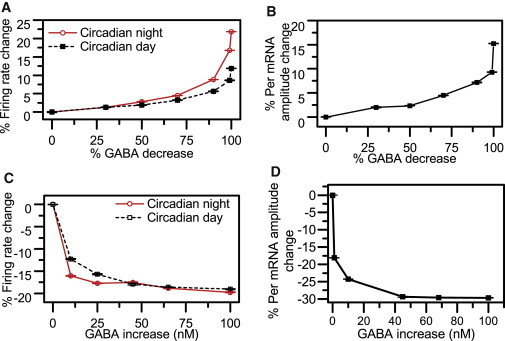
Circadian behavior of the SCN population as a function of GABA concentration. For each GABA concentration, the mean (circle) and SD (error bars) were computed from 10 independent runs. (A) The mean firing frequency of 400 cells changes during the subjective night (solid line) and day (dashed line) as a function of % GABA decrease. (B) Mean Per mRNA amplitude versus % GABA decrease. (C) Mean firing frequency of model population during the subjective night (solid line) and day (dashed line) as a function of GABA increase. (D) Mean Per mRNA amplitude versus GABA concentration increase.

Additional simulations involved the incremental increase of GABA binding to the cell surface. Across 10 independent runs implemented for each GABA concentration, values of the SI measure and the average period were observed to remain constant as GABA concentrations increased. In contrast, progressively higher GABA levels were observed to produce dose-dependent decreases in firing frequency during both the subjective day and night (Fig. 4 C), in agreement with experimental data (48,49). Decreased neuron excitability can be correlated with increased IPSCs as a result of elevated GABA levels. Mean Per mRNA amplitudes were also observed to decrease in a concentration-dependent manner (Fig. 4 D), as GABA administration led to decreased Per mRNA levels during the subjective day and had a minimal effect during the subjective night. These model predictions are in accord with previous reports of suppression of Period gene expression during the subjective day due to GABA_A receptor activation (50).

GABA-elicited responses as a function of cytosolic chloride content

We varied the mean intracellular chloride concentration to investigate its effects on GABA-elicited responses and circadian behavior. Increasing cytosolic Cl⁻ concentrations directly affected the transmembrane chloride gradient and hence the current flow direction. Therefore, progressively higher Cl⁻ concentrations gradually decreased inhibitory current levels and finally shifted the action of GABA on neuronal discharge from inhibition to excitation (Fig. 5 A). These model predictions are in agreement with findings that GABA-elicited currents depend on cytosolic Cl⁻ concentrations (19,20). Additionally, increasing Cl⁻ levels were found to produce higher resting potentials causing a gradual depolarization of the cell membrane (Fig. 5 B). Due to the simultaneous elimination of IPSCs and the depolarization of the cell membrane, the neuronal firing frequency of the population was observed to increase in a dose-dependent manner, with a larger effect seen during the subjective night than during the day (Fig. 5 C) as Cl⁻ concentrations were increased. Mean Per mRNA amplitudes also demonstrated concentration-dependent effects, as progressively higher Cl⁻ concentrations led to increased Per mRNA levels during the subjective day but had no effect during the subjective night (Fig. 5 D).

Figure 5.

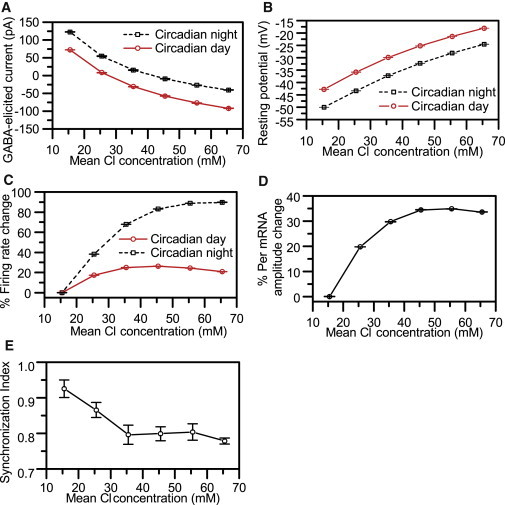
Effect of increasing intracellular Cl⁻ concentrations on circadian behavior. For each Cl⁻ concentration, the mean (circle) and SD (error bars) were computed from 10 independent runs. (A) GABA-elicited currents during subjective night (dashed line) and day (solid line) versus increasing cytosolic chloride concentration. (B) Neuron membrane potential as a function of intracellular chloride during the subjective night (dashed line) and day (solid line). (C) % Mean firing rate change of 400 cells during the subjective night (dashed line) and day (solid line) as a function of cytosolic chloride concentration. (D) % Mean Per mRNA amplitudes versus increases in Cl⁻. (E) The SI at the 10th cycle as a function of cytosolic chloride concentration.

Intracellular Cl⁻ levels were observed to affect the system synchrony and average period of the model SCN population. Our simulations predicted decreased coordination of individual oscillators across the network as a function of increasing Cl⁻ concentrations. SI values were observed to gradually decrease from 0.93 to 0.78 with progressively higher Cl⁻ levels (Fig. 5 E). These model predictions may be relevant to the observation that separating the dorsal and ventral SCN abolishes synchrony in the dorsal SCN, which is the primary region in which GABA-elicited excitatory responses have been recorded (40). The average period of the model system monotonically decreased from 23.3 to 22.4 h due to increases in cytosolic Cl⁻ (Fig. S4). Our model predictions can be experimentally validated by recording the system response while imposing step reductions in the Cl⁻ gradient across the neuron membrane. Such reductions can be practically implemented by gradually decreasing the extracellular Cl⁻ concentration.

Discussion

We developed a multicellular population model of the mammalian core circadian clock that is heterogeneous with respect to uncoupled rhythmic behavior, single-cell periodicity, and neurotransmitter release. An important characteristic of the SCN is its ability to perceive and adapt to various light and dark schedules. Such effects are not currently included in our model but will be the focus of future work. The heterogeneous population was observed to self-synchronize in conditions of constant darkness and produce coherent rhythms in Per mRNA concentrations and firing rates despite the lack of a photic driving signal. The SI rapidly increased within the first 4 days and then slowly approached an asymptotic value of ∼0.93, comparable to data collected from SCN slices (32).

Cytosolic Ca²⁺ is regarded as a critical element of the circadian clock, which is postulated to participate in intracellular signaling mechanisms (9) that affect circadian behavior (51). To test this hypothesis, we varied intracellular calcium levels within individual oscillators. Amplitude reductions in Per mRNA and neural firing across the population accompanied by a decrease in network synchronicity were observed as cytosolic Ca²⁺ concentrations were gradually reduced. These model predictions may be relevant to experimental studies demonstrating abolishment of mean Per mRNA rhythms as a function of increasing concentrations of Ca²⁺ buffer (10). Our simulations therefore suggest that the observed elimination of a collective Per gene expression rhythm across the population can be attributed to reductions in both the amplitude of individual oscillating signals and the system synchrony. Progressively lower intracellular Ca²⁺ concentrations were further seen to decrease the average period of the model system while producing increased SDs of individual neuron periods across the network. This model prediction is comparable to experimental findings of shorter periods with decreasing cytosolic Ca²⁺ concentrations (10). Although experimental data on the effects of increasing Ca²⁺ concentrations are not currently available, our model provides a novel (to our knowledge) computational tool that is able to predict system responses as intracellular Ca²⁺ levels gradually exceed their physiological range within the cytosol.

VIP is a critical neuropeptide that is involved in the generation and synchronization of circadian rhythms (11). We conducted simulations in which the VIP concentration was varied from its nominal value, and successfully replicated a number of experimental observations. Simulations of VIP blockade produced system behavior characterized by reduced synchronicity (SI = 0.1) and low-amplitude oscillations, in similarity to experimental studies (11,44,46). We further tested the effects of constitutive VIP application, for which experimental data are not currently available. The model predicted dose-dependent increases in Per mRNA and firing-rate amplitudes accompanied by reduced synchrony and mean period across the network as the VIP concentration incrementally increased. We were able to experimentally validate these model predictions by applying constant VIP concentrations over 24-h periods while obtaining bioluminescence recordings of Per gene activation by multielectrode arrays on SCN slices.

We varied the amount of GABA binding to the cell surface of individual SCN neurons to compare the model output with experimental data and further test the validity of the model. Incrementally increasing GABA levels led to decreased neural firing frequencies and Per mRNA amplitudes in a concentration-dependent manner, consistent with the literature (48–50). Simulations of incrementally decreasing GABA concentrations produced higher firing rates and Per mRNA amplitudes, as shown experimentally (48). System synchronization and population average periodicity were independent of GABA levels across the network, as values of the SI measure and the average period remained constant over a wide range of GABA concentrations. This model prediction is in agreement with experimental findings (22) suggesting that although GABA controls circadian amplitudes of neuronal rhythms, it is not required for synchrony among SCN neurons.

Several experimental studies have reported excitatory responses in a subset of neurons within the dorsal SCN depending on the circadian timing of GABA administration (18,19). It has been postulated that this variability in GABA-elicited responses results from changes in the transmembrane chloride gradient, which determines the direction of current flow and hence the inhibitory or excitatory nature of the response (19,20). To investigate this hypothesis, we varied the mean intracellular chloride concentration to investigate its effects on GABA-elicited responses and circadian behavior. Increasing Cl⁻ concentrations were shown to progressively decrease IPSCs and ultimately shift the effects of GABA from inhibitory to excitatory. Additionally, progressively higher Cl⁻ levels were observed to increase the membrane resting potential and cause a gradual depolarization. As expected, simultaneous elimination of IPSCs and membrane depolarization produced dose-dependent increases in firing rates across the population (48). Similarly, our model predicted increasing Per mRNA amplitudes as a function of increased Cl⁻ concentrations. This prediction is comparable to experimental work that demonstrated a positive correlation between neural firing rate and core-clock gene transcriptional activity (53).

Our simulations further predicted decreased coordination of individual single oscillators across the network as a function of increasing Cl⁻ concentrations. These model predictions may be relevant to the observation that separating the dorsal and ventral SCN abolishes synchrony in the dorsal SCN, which is the primary region in which GABA-elicited excitatory responses have been recorded (40). The average period of the model system monotonically decreased from 23.3 to 22.4 h due to increases in cytosolic Cl⁻. Our model suggests that intracellular Cl⁻ concentrations directly affect GABA-elicited currents, further influencing system behavior and synchrony.