Hybrid Steered Molecular Dynamics-Docking: An Efficient Solution to the Problem of Ranking Inhibitor Affinities Against a Flexible Drug Target

Abstract

Existing techniques which attempt to predict the affinity of protein-ligand interactions have demonstrated a direct relationship between computational cost and prediction accuracy. We present here the first application of a hybrid ensemble docking and steered molecular dynamics scheme (with a minimized computational cost), which achieves a binding affinity rank-ordering of ligands with a Spearman correlation coefficient of 0.79 and an RMS error of 0.7 kcal/mol. The scheme, termed Flexible Enzyme Receptor Method by Steered Molecular Dynamics (FERM-SMD), is applied to an in-house collection of 17 validated ligands of glutamate racemase. The resulting improved accuracy in affinity prediction allows elucidation of the key structural components of a heretofore unreported glutamate racemase inhibitor (K_i = 9 µM), a promising new lead in the development of antibacterial therapeutics.

1 Introduction

The grand challenge of computer-aided drug discovery and design is the ability to rank-order the binding affinity of known ligands/inhibitors at a reasonable level of both accuracy and precision. This allows one to predict potential chemical modifications of an inhibitory scaffold class with high confidence, which offers a potentially transformative tool for medicinal chemists. However, current methods have not displayed substantial progress.

Docking and scoring methods used on single crystal structures (or accurate homology models) have been shown to perform well at both ligand placement and distinguishing binders from non-binders (i.e., enrichment studies). Furthermore, docking and scoring has worked well in the realm of virtual screening (VS), where the goal is to enrich test sets with novel binding scaffolds with approximately micromolar equilibrium dissociation constants.^[1] However, problems persist here as well, as recently reviewed by Martha Head.^[1] Nevertheless, all current docking and scoring schemes completely lack the ability to rank-order drug leads at the level of resolution necessary for efficient drug optimization. There are a plethora of docking packages and approaches that account for receptor flexibility,^[2–7] by employing various versions of ensemble docking, and show improvements in ligand placement versus single crystal structure cross-docking. However, it should be emphasized that none of these approaches has demonstrated any improvements in rank-ordering relative ligand binding affinities. The current consensus is that affinity rank-ordering is beyond the means of any simple scoring function, even when flexibility is taken into account.^{[1, 8–10]}

Late-phase drug discovery depends critically on the ability to predict how affinity to a 3D pharmacophore changes with the structure of the lead compound. The particular role that relative free energy calculations play in the drug lead optimization process has been recently reviewed.^{[9, 11]} More sophisticated treatments to directly calculate the free energy of binding of a ligand to a target have made noteworthy progress in the last decade, and have recently been reviewed by Shirts et al.^[9] On the other hand, direct free energy calculation methods based on molecular dynamics (MD) simulations such as thermodynamic integration (TI)^[12] and weighted histogram analysis method (WHAM)^{[13, 14]} are both technically challenging to implement and usually very computationally expensive. Furthermore, there is not yet a wide consensus that such methods meaningfully improve rank-ordering, relative to well designed endpoint methods that utilize implicit solvation models (MD/MM/PBSA/GBSA).^[9,15] Additionally, even the most inexpensive TI and WHAM-based calculations of binding free energies are certainly not applicable to large numbers of compounds.

Hybrid MD/Docking studies have recently shown progress at improving affinity rank-ordering relative to docking against a single crystal structure,^[16] but rely on multiple docking simulations for every ligand tested. Here we present a novel hybrid method for accurate and precise affinity rank-ordering of ligands against a challenging enzyme drug target, which employs a combination of steered molecular dynamics (SMD) simulations, ensemble docking and solvation free energy calculations of the enzyme. The method has been termed Flexible Enzyme Receptor Method by Steered Molecular Dynamics (FERM-SMD), and gives outstanding correlations with experimental values at a fraction of the simulation costs of methods that rely on extensive MD-based sampling (vide infra). SMD yields information beyond the normal MD timescale (10 s to 100 s of ns) by applying a harmonic force potential along a defined path. Although the magnitude of the forces and timescales employed may not be compared to the experimental (i.e., in vitro) studies, it has been shown that SMD simulations have accurately predicted macromolecular behavior, often with short simulation times. SMD simulations have been used to determine a variety of macromolecular phenomena, including binding/unbinding of small molecule-protein complexes, protein-protein adhesion and stretching of muscle proteins.^[17–20]

The receptor employed to test this hybrid SMD/Docking approach to ligand affinity rank ordering is the enzyme glutamate racemase (GR), which catalyzes the reversible isomerization of l- to d-glutamate,^[21] a key step in synthesis of the peptidoglycan cell wall of Gram-positive and -negative bacteria,^[22] and is accordingly a recognized drug target for development of antibiotics. GR is a member of the pyridoxal phosphate-independent family of racemases and epimerases, which have been the subject of recent mechanistic and structural advances.^[23–30] Knockout studies have shown that the absence of an active form of GR is lethal for the target cells.^[31] Despite attempts from several academic and pharmaceutical labs, progress in lead discovery and therapeutic development based on GR inhibition has been limited. Successful leads (IC₅₀’s in the low µM- and high nM-range) are limited to a competitive class of 4-substituted glutamate analogs,^[32] an uncompetitive class of pyrazolopyrimidinediones,^[33] and two competitive inhibitors located via virtual screening against GR transition state structures.^[29] GR is a challenging system to study in silico due to its inherent flexibility. This is not an uncommon problem with enzyme targets, and undermines the core assumption of the majority of tools used in CADD (i.e., drug design targeting a unique receptor structure). The ligand set employed here, a total of 17 compounds, is composed entirely of validated, competitive GR inhibitors (with the exception of d-glutamate, the native substrate) discovered in-house from previous virtual screening campaigns against GR as described by Spies and co-workers.^[26]

Contrary to the technique successfully employed by Spies et al.^[26] as well as Whalen et al.^[29] which focuses on targeting an enzyme conformation related to the chemical step of the catalytic cycle (i.e., the catalytic transition state), this study attempts to represent receptor flexibility with conformations sampled in the process of substrate unbinding. In this study, we present the utilization of FERM-SMD in the elucidation of the structure-affinity relationship of a novel competitive GR inhibitor (heretofore unreported), which displays a K_i of 9 µM (the lowest K_i yet reported for a GR inhibitor). Importantly, the rank-ordering results presented here meet or exceed a number of critical accuracy and precision thresholds often cited as performance standards in CADD.

2 Materials and Methods

2.1 Materials

Inhibitor compounds were acquired from a variety of vendors. Chemical or common names are listed and catalog numbers as well as numeration utilized in the current study is noted in parenthesis. Croconic acid (2, LT00453399) was purchased from Labotest (Bremen, Germany). 4-Hydroxy-1,3-benzenedisulfonic acid (3, BAS 00124393) was purchased from Asinex (Moscow, Russia). From Sigma Aldrich (St. Louis, MO) we obtained the following: α-ketoglutarate (5, K1875), tartrate (16, 228729), d-glutamate (4, G1001), d-glucuronic acid (8, G5269), citrate (17, C8532), 4-pyridazine carboxylic acid (12, 297763), (R)-(+)-2-pyrrolidone-5-carboxylic acid (13, 422614), 2-hydroxy-5-nitrobenzenesulfonic acid (11, S364169), chloroaniline-4-sulfonic acid (6, S438774), and benzimidazole-2-sulfonic acid (1, 530646). Both dipicolinic acid (9, 02321) and l-pyroglutamic acid (14, 83160) were supplied by Fluka, while formylbenzene-sulfonic acid (10, S0122) and methyl-propene-sulfonic acid (15, M1408) were purchased from TCI America (Portland, OR). Compound 13a (7) was generously provided by Igor Komarov (Kyiv Taras Shevchenko University, Kyiv, Ukraine).^[60] The %-purity and method of purity analysis for each active compound is listed in Table S1. Concerning the coupled-enzyme assay, all reagents were purchased from Sigma Aldrich: iodonitrotetrazolium (I8377), diaphorase (D5540), ATP (A7699), NAD⁺ (N7004), and l-glutamate dehydrogenase (G2501). All reagents related to buffer preparation for protein purification and circular dichroism were purchased from Sigma-Aldrich. Amicon centrifugal filtration devices were purchased from Millipore (Billerica, MA). Finally, HIS-Select Cobalt Affinity Gel (H8162) was purchased from Sigma-Aldrich.

2.2 Protein Expression and Purification

A 10 mL starter culture of LB medium with 100 µg/mL ampicillin was prepared from the stock E. coli BL21 (DE3) cells containing pET-15b plasmid (cells and plasmid acquired from Novagen/EMD Biosciences [San Diego, CA]) with the gene encoding RacE from B. subtilis and grown overnight at 37°C with rotation. The 10 mL starter culture was back-diluted into 1 L fresh LB medium with 100 µg/mL ampicillin. Cells were grown at 37°C with shaking until the optical density at 600 nm reached 0.5–0.8. Protein expression was induced upon addition of a final concentration of 0.1 mM IPTG. Following induction, cells were grown for an additional 16–20 h at 37°C with shaking (16 °C for mutant proteins). Cells were harvested by centrifugation at 5000 × g for 15 min. Cell lysis was achieved through sonication (3 × 20 s cycles, 23 kHz and 20 W), using a 100 Sonic Dimembrator (Fisher Scientific). Insoluble materials were pelleted by centrifugation at 20000 × g for 30 min and clarified lysate was applied to batch-style affinity chromatography using His-Select Cobalt Affinity Gel. Concentrated eluant was incubated at 37°C for 15 min with 1 mM ATP and 1 mM MgCl₂ to remove high molecular weight contaminants suspected to be chaperones. Eluant was then diluted 10-fold with H₂O and submitted to ion exchange chromatography using a BioRad Uno Q1 column on a BioRad BioLogic DuoFlow HPLC. Pooled fractions were then exchanged into protein storage buffer (50 mM Tris, 100 mM NaCl, 0.2 mM DTT, pH 8.0) and concentrated utilizing a 10000 MWCO Amicon centrifugal filter device. Finally, protein stocks were stored at a final concentration of 7–10 mg/mL with 20% glycerol at −20°C.

2.3 Enzyme Kinetics via Circular Dichroism

Racemization of d-glutamate to l-glutamate by glutamate racemase (GR) was assayed by measuring molar ellipticity at 225nm continuously for 15 min using a JASCO J-720 spectropolarimeter (JASCO Inc., Easton, MD). IC₅₀ curves were acquired in the presence of 0.5 µM GR and 1 mM d-glutamate with varying concentrations of the inhibitor compound. Data was analyzed using the accompanying software, JASCO Spectra Manager v1.54A. K_i values were acquired through global fitting of three Michaelis–Menten curves conducted in the presence of three distinct concentrations of inhibitor and 0.5 µM GR. Global fitting to varying inhibition models was completed using GraphPad Prism v5. All assays were performed at 25°C.

2.4 Enzyme Kinetics via the Coupled-Enzyme Assay

For compounds whose contribution to the spectropolarimeter noise was too great to acquire accurate kinetic curves (i.e., compounds required in excess or compounds with substantial optical activity), the previously established coupled-enzyme assay for measurement of d-glutamate to l-glutamate racemization was utilized.^[61] IC₅₀ curves and K_i values were acquired in the same manner in the presence of 0.38 µM GR. Absorbance at 500 nm (production of reduced INT) was measured using a Varian Cary-300 UV-VIS spectrometer (Agilent Technologies). Data was acquired using the accompanying Cary Kinetics software. All assays were performed at 25°C.

2.5 Classical MD Simulations

The molecular dynamics simulations were performed with the YASARA Structure package version 9.11.9 (YASARA Biosciences).^[56] A periodic simulation cell with dimensions of 54.99 Å, 64.39 Å, and 57.77 Å was employed with explicit solvent, using the monomer (C chain) of PDB 1ZUW (B. subtilis RacE GR with ligand d-glu). The AMBER03 force field was used with long-range electrostatic potentials calculated with the Particle Mesh Ewald (PME) method, with a cutoff of 7.864 Å.^[62–64] The substrate force field parameters were generated with the AutoSMILES utility,^[57] which employs semi-empirical AM1geometry optimization and assignment of charges, followed by assignment of AM1BCC atom and bond types with refinement using RESP charges, and finally the assignments of general AMBER force field atom types. The hydrogen bond network of GR is optimized using the method of Hooft and co-workers,^[65] in order to address ambiguities from multiple side chain conformations and protonation states that are not resolved by the electron density. YASARA’s pKa utility was used to assign pK_a values at pH 7.0.^[66] The box was filled with water, with a maximum sum of all bumps per water of 1.0 Å, and a density of 0.997 g/mL. The simulation cell was neutralized with NaCl (0.9% final concentration; % by mass). Waters were deleted to readjust the solvent density to 0.997 g/mL. A short MD was run on the solvent only. The entire system was then energy minimized using first a steepest descent minimization to remove conformational stress, followed by a simulated annealing minimization until convergence (<0.05 kJ/mol/200 steps). The MD simulation was then initiated, using the NVT ensemble at 298 K, and integration time steps for intramolecular and intermolecular forces every 1.25 fs and 2.5 fs, respectively.

2.6 Steered Molecular Dynamics Simulation

The singular steered MD simulation was carried out using the YASARA Structure package v9.11.9. Before applying the steering potentials in the production phase, the classical MD procedure, described above, was executed. The production phase consisted of external steering forces applied to the center of mass of the GR enzyme and the glutamate ligand. A vector leading out of the constricted entrance to the active site of GR was selected (Shown in Fig. 3B, depicted as a red arrow) for constant velocity pulling of the glutamate ligand into bulk solvent. The velocity of the ligand in the pulling vector was set in a window of 0.2 to 0.5 Å/ps using a scaled pulling force of 5000 pN. The large magnitude of the applied steering force constant allows one to make a stiff spring approximation, which has been shown to significantly minimize fluctuations of the pulling coordinate^[67] from one trajectory to another. The external force was applied only along the pulling vector. The glutamate ligand was not constrained in the plane orthogonal to the pulling vector. The forces and the velocity in the pulling direction were calculated at every time step. The entire production simulation consisted of ~50 ps, which resulted in a translocation of the glutamate ligand a distance of ~30 Å from the active site of GR.

Figure 3.

a) Area of active site entrance and corresponding protein solvation energy at varying time points along the trajectory of a Steered Molecular Dynamics simulation. The x-axis corresponds to the distance between the center of the mass of d-glutamate and the center of mass of GR as d-glutamate is being pulled out of the active site. The area of the active site was calculated as explained above. Protein solvation energy was calculated for each time-point using the Poisson–Boltzmann method with an internal dielectric of 25, a solvent dielectric of 78, and a salt concentration of 0.1 M. The region shaded in yellow represents entrance areas observed for inhibitor-GR complexes after standard MD simulation. Twelve structures were selected arbitrarily for analysis. Arrows indicate structures selected for use in ensemble docking. b) The user-defined exit vector for d-glutamate (shown in stick rendering) from the active site of B. subtilis GR employed for SMD unbinding simulations is shown as a red arrow leaving the active site entrance. The external force was applied only along the pulling vector. The glutamate was not constrained in the plane orthogonal to the pulling vector (see Computational Methods section for a detailed description of the SMD unbinding).

2.7 Preparation of Docking Receptors

Twelve structures were selected from the SMD simulation at regular time intervals and active site entrance area was approximated by calculating the area of a plane defined by four points (the γ-carbons of Pro41, Pro44, Pro146, and Pro150). Three structures were selected from that subset to reflect three points, approximately equidistant, along the continuum of active site entrance areas. The structures correspond to the following distances between the centers of mass of the glutamate molecule and GR: 28.8, 43.7, and 46.7 Å, respectively. Structures were prepared for virtual docking by first deleting all water molecules, salt ions and the substrate, d-glutamate. A simulation cell was centered on the catalytic cysteine residues, Cys74 and Cys185, and dimensions of the cell were adjusted for individual structures to encompass the entirety of the active site. The same preparation was used for docking to the crystal structure of RacE from B. subtilis (1ZUW, chain C).

2.8 Virtual Docking of Known GR Ligands

Ligands were constructed and minimized in MOE v2009.10^[68] and imported into YASARA for virtual docking. YASARA v9.11.9^[56] employs AutoDock 4^[58] in its docking functionality. AutoDock uses a Lamarckian genetic algorithm to sample ligand conformations and binding modes. The following general docking parameters were used: 25 independent docking runs, each with a total of 2.5 × 10⁶ energy evaluations, a torsional degrees of freedom value of 8, grid point spacing was left at the default of 0.375 Å, and the force field selected was AMBER03. Specific to the genetic algorithm, the following parameters were used: a population size of 150, 2.7 × 10⁴ generations, an elitism value of 1, a mutation rate of 0.02, and a crossover rate of 0.8. Final poses were considered distinct if they varied by > 5 Å RMSD. AutoDock uses a semi-empirical free energy force field to predict free energies of binding which accounts for intermolecular and intramolecular energies, as well as charge-based desolvation. Calculated binding energies and corresponding binding constants, acquired from the docking output file, were applied to the FERM-SMD correction equation (see Results). All correlation datasets are fit to a semi-log equation and indicated R values represent the Spearman’s coefficient of rank correlation as calculated by GraphPad Prism v5.0.

2.9 Protein Solvation Energy Calculations

The protein solvation energy was calculated for each structure attained from the SMD simulation using the Poisson–Boltzmann method. In the Poisson–Boltzmann method, the calculated solvation energy is based on numerical solution of the differential Poisson equation (also called the finite difference method) and the solvent is represented as a continuum having a relatively high dielectric constant, while the protein and ligand may be viewed as point charges projected onto a grid in a low dielectric continuum. Structures were prepared by deleting all water molecules, salt ions and substrates. The internal dielectric was set to 25, which resulted in more consistent energy predictions between structures and was thus determined to be most representative for the highly-hydrophilic glutamate racemase active site. The overall trend in solvation energies over the span of the SMD was the same with an internal dielectric of 2 (Fig. S8). The external dielectric was set to 78 and the salt concentration was set to 0.1 M. Solvation energies were reported in kcal/mol.

3 Results

3.1 Discovery of Glutamate Racemase Inhibitors of Varying Scaffolds and Potencies

All ligands referred to in this study fall into two categories based on their method of selection for use: 1) those identified from a previous in silico screening study and 2) glutamate analogs (see Supporting Information Data for a full account of the source of active compounds). The group of ligands identified from virtual screening can be further categorized into: 1) hits originally ranked in the virtual screening study and 2) hits derived from ranked compounds but not present in the original library of compounds. Co-crystal structures exist only for compounds 4 (d-glutamate, PDB 1ZUW), 16 (citrate, PDB 2JFV), and 17 (tartrate, PDB 2JFW). Despite being co-crystallized with GR previously, inhibition by compounds 16 and 17 had not been characterized until now. All compounds derived from virtual screening underwent full structural characterization as well as controls for non-specific inhibition, which can be found in the Supporting Information (Supporting Information, Fig. S6 and S7).

All compounds were assayed for inhibition against glutamate racemase from Bacillus subtilis (RacE, abbreviated in this study as GR) in-house. Compounds 2, 3, and 9 were presented previously as being competitive inhibitors of BsGR by our group.^{[26, 29]} Compounds 1, 5–8, and 10–17 are presented here for the first time as being inhibitors of GR. Compound 4 is the d-enantiomer of the native substrate, glutamate. Inhibitors discovered here range in potency from low-µM (K_i = 9 µM) to high-mM (IC₅₀ = 50+ mM), a range of 5 log-units (Supporting Information, Fig. S4). Additionally, this set of 17 ligands is unique in its wide diversity of structures (see Supporting Information Table S1 for all structures), a testament to the flexibility of GR in that the active site can accommodate inhibitors with solvent accessible volumes ranging from 307 ų to 482 ų. Worth high-lighting is a promising new class of GR inhibitors represented by 1 and 6. Compound 1 is particularly impressive in that it possesses a ligand efficiency of 0.53 kcal/mol/heavy atom and is a verified competitive inhibitor (Fig. S4, as verified by global fitting to varying inhibition models). This high ligand efficiency may facilitate the development of a nM inhibitor that maintains a low molecular weight.^[34] The scaffolds of these sulfonate-containing aromatic compounds offer an assortment of possible modifications that have the potential of increasing the potency into the nM-range. Additionally, this scaffold lies in a similar chemical space as known therapeutics (particularly, the recently reviewed class of sulfa drugs^[35]), indicating an increased likelihood of bioactivity.^[36–40]

3.2 Docking to the GR Crystal Structure Gives Little-to-no Information About Rank Order of the Ligand Set

Docking of inhibitors to a single crystal structure of glutamate racemase from B. subtilis (PDB 1ZUW) results in a poor Spearman correlation coefficient (denoted, R) between predicted and actual binding energy (Fig. 1, R = 0.53). Specifically, this method of docking and scoring more often errs on the side of overestimating the potency of inhibitors (Table S1 for affinity predictions). A handful of inhibitors displayed inhibition in the low mM range (IC₅₀ = 1–10 mM) but were predicted by docking to possess binding constants in the hundreds and in some cases even tens of µM. This trend of overestimation of affinity would indicate that an unfavorable component of complex formation is not being accounted for in this method. An important corollary of the above is that the RMS error (1.2 kcal/mol) from the linear regression is beyond the limit for what is considered “practical accuracy” (1 kcal/mol),^{[9, 41]} which reduces the usefulness of this correlation in structure-based drug design.

Figure 1.

Correlation of binding energy for 17 inhibitor-GR complexes as predicted by docking to the crystal structure and experimental-derived binding affinities (as K_i or IC₅₀ values), many of which are presented here for the first time. Experimental results were determined using circular dichroism or a pre-established colorimetric coupled-enzyme assay, depending on the optical activity of inhibitor compounds. Docking studies were conducted using a single monomer of GR from the previously solved co-crystallization of GR from B. subtilis, RacE, with d-glutamate (1ZUW). Ligands were allowed to explore space limited to the GR active site. Only the predicted binding energy of the top-ranked binding pose for each inhibitor is represented on the graph. Data is fit to a semi-log regression and the Spearman correlation coefficient, R, is noted. The ± 1 kcal/mol threshold is marked (dotted lines). Classical MD simulations of GR-ligand complexes show receptor heterogeneity at the equilibrated active site.

Half-nanosecond MD simulations were conducted on the top-docked poses of all GR-inhibitor complexes, following simulated annealing energy minimization, in an attempt to better represent the true complex and improve binding energy predictions. Time series data for all of the MD trajectories of GR-inhibitor complexes are located in Figure S5 of the SI. We observed that the final equilibrated complexes varied widely in their degree of opening at the active site (i.e., the area of the active site entrance). The area is defined by the γ-carbons of four proline residues that form a plane at the mouth of the active site (residues 41, 44, 146 and 150). The spectrum of areas induced by the presence of inhibitor ranged from 47.4 Ų (for 1) to 63.6 Ų (for 7).This metric for opening is also used in the SMD studies (vide infra). Figure 2 illustrates the opening metric.

Figure 2.

Image of GR (white surface area) with 3 (stick, blue/red/green) bound in active site. The γ-carbon atom of four proline residues (red; Pro41, Pro44, Pro146, Pro150) designate the perimeter of the active site entrance. Five distances (yellow) composing two irregular triangles are calculated to approximate the area of the active site entrance of varying inhibitor-GR complexes after energy minimization and 500 ps of molecular dynamics simulation.

It is reasonable that large changes in the degree of opening of the active site, and generally large changes in the structure of GR (which seem to be captured or represented in the distribution of equilibrated GR-ligand complexes) will alter physical parameters that determine the ligand affinity. For instance, one would expect large changes in the protein solvation energy of a very open GR complex versus a closed complex, due to its very polar and H-bond donating interior. This question is best addressed by the use of steered MD simulations (vide infra), since high energy transitions on the ligand binding trajectory can be obtained without prohibitively long simulation time.

3.3 Steered MD Unbinding Simulation of the Native Substrate (Glutamate) Shows a Correlated Pattern Between Protein Solvation Energy and Area of Active Site Opening

In order to investigate if there is a relationship between the degree of opening and the protein solvation energy we employ SMD to capture a reasonable ensemble for the entire unbinding process for the substrate, d-glu. By plotting the area of the active site entrance and the protein solvation energy as a function of the distance between glutamate and GR (obtained from our SMD simulations), a pattern between protein conformation and solvation (Fig. 3) becomes apparent. The active site entrance area opens incrementally as glutamate is being pulled out of the active site, suggesting that the active site is closed tightly in the Michaelis–Menten complex and conformational changes must occur to accommodate the passage of glutamate back through the entrance during product release. The entrance area reaches a maximum when the glutamate center of mass is 46.7 Å from the center of mass of GR and this maximum is immediately followed by a decrease in entrance area indicating the relaxation of GR upon complete substrate release into bulk solvent. This SMD simulation agrees with the previous notion that GR undergoes conformational changes during its catalytic cycle, and now shows that these conformational changes correspond to significant changes in the protein solvation energy, which will directly affect complex affinity (i.e., more negative protein solvation energies will contribute to weaker ligand binding; vide infra).

The data from the SMD simulation in Figure 3 covers a relatively large range of openings, relative to the areas of opening seen in equilibrated GR-ligand complexes obtained from classical MD simulations (Fig. S5). The range of openings seen in GR-ligand complexes from classical MD is depicted by the yellow shaded area in Figure 3 (i.e., opened GR structures captured by ligands may be a subset of structures in the SMD d-glu-unbinding trajectory). If the distribution of conformations of GR is relatively independent of the nature of any particular active site ligand, then a single SMD unbinding simulation with the natural substrate (which is also the ligand in the original co-crystal structure) would be a sufficient approximation of the liganded ensemble of GR, and obviate the need for unbinding simulations for any particular ligand of interest. In other words, this simple, single SMD with d-glu is used to construct a new target, in lieu of the crystal structure. It is important to stress that the SMD simulation is only ever performed one time (i.e., on the native substrate), which is used to prepare the new target ensemble, which will be docked against the library of ligands used in this study.

3.4 The Flexible Enzyme Receptor Method by Steered-MD Docking (FERM-SMD)

The following docking and scoring method incorporates the structural data obtained from the SMD procedure described above for the binding trajectory of the native substrate with GR in order to improve ligand rank ordering relative to classical docking (where only a single structure is used as a receptor). The dominant trend in the erroneous rank-ordering of classical docking with GR is both the assignment of high affinities to weak inhibitors and the large scatter in the correlation between predicted and experimental binding energies. The incorporation of an ensemble of structures taken from the GR-substrate unbinding trajectory allows one to largely correct for these problems with classical docking, as described below.

Figure 3 clearly shows the trend in solvation energy of GR with opening. When calculating ligand binding free energy values with endpoint methods (reviewed recently^[42]), ΔG_bind is composed of constituent parts of a thermodynamic box that involves solvation of the individual components. The binding energy expression is:

$$\mathrm{\Delta }{G}_{\text{Bind},\text{Solv}}=\mathrm{\Delta }{G}_{\text{Bind},\text{Vacuum}}+\mathrm{\Delta }{G}_{\text{Solv},\text{Complex}}-(\mathrm{\Delta }{G}_{\text{Solv},\text{Ligand}}+\mathrm{\Delta }{G}_{\text{Solv},\text{Receptor}})+\mathrm{\Delta }{G}_{\text{np}}$$ (1)

Equation 1 shows that the more negative the value of ΔG_bind,solv then the more positive will be the overall ΔG_{solv,receptor} for a given ligand, assuming all other parameters are constant. Thus, structural changes in the receptor that lead to more favorable solvation energies will result in more unfavorable (i.e., weaker) binding of a given ligand, assuming that the solvation energy of the GR-ligand complex is relatively unchanged.

Our hypothesis is that this is the major feature that is causing over estimation of ligand affinity for GR using classical docking. For the case of GR, this means that the larger openings of GR-ligand complexes and their more favorable solvation energies of their corresponding protein component would lower binding affinities of ligands that populate those states (assuming that the GR-ligand complex solvation energy is not greatly different than the fully closed state). This concept is illustrated in Figure 4, which depicts a central manifold that represents the native substrate (dark grey structure) unbinding trajectory, which has been elucidated with SMD (Fig. 3a). A substrate analog (black structure, upper manifold of Fig. 4) has a high affinity for the closed state (which closely matches the crystal structure), and little affinity for more opened states; this represents a situation where binding affinity would be well predicted using classical docking methods, and approximates a true positive. On the other hand, some compounds (light grey structure, lower manifold of Fig. 4) will have an affinity for multiple structures along the ligand unbinding trajectory. To the extent that open forms are highly complementary to a given ligand, the classical docking assumptions fail, for numerous reasons, as outlined above. Therefore, compounds that “capture” or form complexes with more open GR structures should be identified and have a weighted docking score that accurately reflects the reduced affinity. A weighting scheme based on a statistical thermodynamically-determined ensemble from SMD is one approach to construct a corrected binding energy calculation. However, energies obtained via SMD are notoriously not reflective of experimental conditions.^{[18, 19]} In the FERM-SMD scheme presented below, the inhibitor-enzyme distribution is determined by a weighting factor based on the relative binding affinity of a given ligand within the SMD ensemble, while the ΔΔG_protein,solv (i.e., the change that occurs in the open state relative to the closed state) is used to correct the predicted binding affinity of each inhibitor-enzyme complex, as described below.

Figure 4.

Scheme for Hybrid Steered Molecular Dynamics-Docking and how it might elucidate rank-order decoys (RODs) amongst a set containing true positives. In the boxed region is a simplified representation of steered molecular dynamics (SMD) including the removal of substrate (dark grey) along the indicated vector (arrow), and resulting in the subsequent opening of GR. Structure ascertained from SMD are then used as receptors in docking of inhibitor 1 (black) and inhibitor 2 (light grey). A true positive (as is the case for inhibitor 1) will result in high affinity binding to the closed for (K_d = X) and low affinity binding to the open form (K_d > X). A rank-order decoy (as is the case for inhibitor 2) will result in high affinity binding to the closed form (K_d = Y) but also high affinity binding to the open form due its ability to also bind an alternate binding mode only present in the open form (K_d < Y).

The FERM-SMD/Docking weighting and correction method is summarized as follows:

$$\mathit{\text{FERMScore}}=-{\displaystyle \sum }[(X_n·a_n)]$$ (2)

$$X_n=\frac{\Delta G_{{\mathit{\text{bind}}}_n}}{\Delta G_{{\mathit{\text{solv}}}_n}-\Delta G_{{\mathit{\text{solv}}}_{\propto }}}$$ (3)

$${\mathrm{\alpha }}_n=\frac{1}{\frac{K_{i_n}}{{\displaystyle {\sum }_{\mathit{\text{Closed}}}^{\mathit{\text{Opened}}}}{K}_{i_n\mathrm{\varnothing }}}}$$ (4)

where, FERMScore is the predicted binding metric (more negative value corresponds to tighter binding); X_n is the correction factor for docking to the n^th structure of an ensemble of target structures obtained by steered MD unbinding of the natural substrate (i.e., a single SMD simulation used for all docking studies); ΔG_bindn is the predicted change in free energy for binding of a given ligand to the n^th structure of an ensemble of target structures obtained from SMD, as described above; ΔG_solvn is the change in solvation energy of the n^th structure of the SMD ensemble, going from a low dielectric constant to that of aqueous solvent, by numerically solving the Poisson–Boltzmann (PB) equation; ΔG_solv∝ is the change in solvation energy of a reference structure of the SMD ensemble (here the most closed or starting structure), going from a low dielectric constant to that of aqueous solvent, using PB approaches (as above); a_n is the weighting factor for docking a given compound to the n^th structure of the SMD ensemble; K_in is the equilibrium dissociation constant obtained for docking a given ligand to the n^th structure of the SMD ensemble using AutoDock. ${\displaystyle {\sum }_{\mathit{\text{Closed}}}^{\mathit{\text{Opened}}}}{K}_{i_n\mathrm{\varnothing }}$ represents a summation of all of the calculated equilibrium constants determined via docking to the SMD ensemble for ligand Ø.

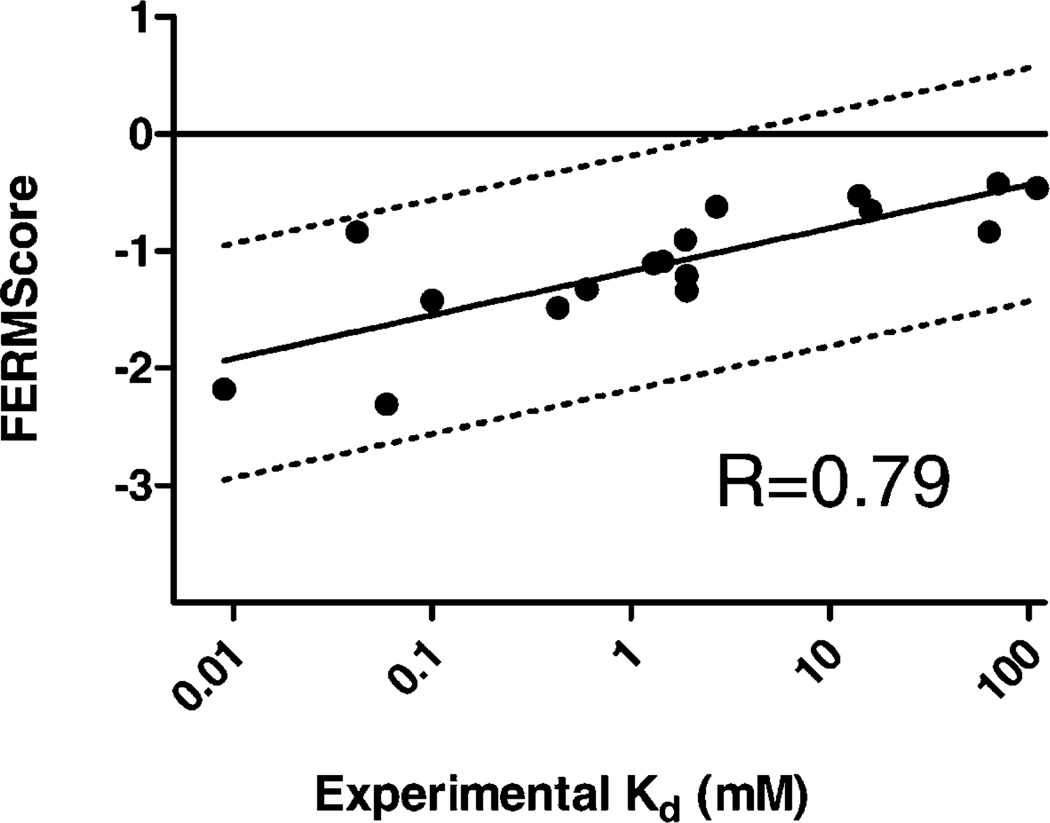
The FERM-SMD/Docking approach is to simply dock any given ligand to representative structures from a single SMD simulation from Figure 3 (performed on d-glu), which are indicated by the black arrows (in Fig. 3A), and span the range from essentially fully closed to the most open (for overlay of structures, see Fig. S1). When applied to the 17-ligand set of GR, the correlation between predicted and experimental binding energies increases to R = 0.79 with an RMS error of 0.70 kcal/mol. This is a significant improvement relative to orthodox docking, in both of the critical areas of R value and the RMS error (i.e., scatter). Importantly, these large improvements were obtained with little additional simulation time (vide infra). This is a noteworthy improvement in the field of predicting ligand affinities and performs well against both expensive free energy approaches (TI and WHAM^{[13, 43, 44]}) and significantly surpasses most end point methods (MD/MM/PBSA/GBSA type^{[15, 43, 45, 46]}) as well as other ensemble MD/Docking methods;^[16] when one considers the improvement in rank-ordering (relative to standard docking) of a set of ligands per simulation time, relative to more expensive techniques, the FERM-SMD/Docking approach is exceedingly attractive. This will be fully discussed below.

In order to explore whether significant improvement in the correlation could be attributed simply to ensemble docking regardless of where receptor structures were acquired, the FERM-SMD/docking method was performed where SMD-derived structures were replaced with three structures acquired from a 16-nanosecond classical MD simulation of an apo-RacE monomer. QR analysis was conducted on snapshots from the classical MD simulation to provide the three most structurally-distinct snapshots and best represent the sampled structural space. QR analysis has been shown previously to successfully distill MD results structurally without losing representation energetically.^{[47, 48]} With all other aspects of the scheme remaining the same, this modified method did not improve upon the correlation achieved by orthodox docking (Fig. S3). This finding reaffirms the ability of SMD to sample a greater structural space and this supports the idea that relatively large global fluctuations are a key parameter in correcting rank ordering with a flexible target. Also worth noting, individual docking to any one of the three structures acquired from SMD does not result in an improvement in the correlation over orthodox docking to the crystal structure (Fig. S2), pointing to the importance of ensemble docking and ruling out the possibility of FERM-SMD’s success being simply the result of a single structure providing a more optimal receptor.

A particularly difficult challenge for any computational method is to rank order congeneric sets. All of the compounds in our 17 ligand set have a low molecular weight (124–260) and negative charges, consisting of carboxylates and/or sulfonates (except 2, which has an oxyanion), with some variation in the number of rotatable bonds. If one examines, for instance the subset of compounds that have single sulfates, and compares the rank-order performance of orthodox docking versus FERM-SMD/Docking (Table 1, see Table S1 for a complete table of predicted and experimental affinities), it is apparent that the former results in a narrowing and incorrect ordering, while the latter results in a spreading out of the affinities that mirrors the experimental trend. It is instructive to examine how the SMD ensemble is used to dock and score compounds into a more realistic rank-ordering. Figure 6 compares the “well-behaved” 1 which possesses a relatively enhanced binding affinity for the closed form of GR (Fig. 6a and 6b) to 10, which tends to partition into more open forms of GR, relative to 1. This differential partitioning would pose serious problems for accurate rank-ordering using classical docking, but is corrected using FERM-SMD scoring.

Table 1.

Predicted and experimental binding constants of select sulfonate-containing ligands to exemplify the superior rank-ordering of the FERM-SMD method.

Compound	Predicted binding	constant[a] (mM)	Actual binding constant (mM)
	Crystal 0nly	FERM-SMD
1	0.29	0.002	0.009
6	0.76	0.44	0.6
10	0.23	0.91	1.9
15	62.0	8.9	63

^[a]Relative binding constants are predicted by docking to the crystal structure (Crystal only) or by docking to the SMD-derived ensemble (FERM-SMD) and calculated using the logarithmic regression shown in the correlations in Figure 1 (y = −0.334 ln(x) + 5.883) or Figure 5 (y = −0.163 ln(x) + 1.194), respectively.

Figure 6.

Example of partitioning of false positive (rank-order) decoys into open forms of GR from the SMD ensemble used in the FERM-SMD/Docking procedure. Panels a and b illustrate the case of a “well behaved” ligand, in that it does not partition into opened structures; Panel a is the ligand map for the top docked pose of 1 to the closed form, which is strongly favored in this case; panel b is the top docked conformation into an opened structure from the GR SMD ensemble, which has a strongly diminished affinity for the target, showing a change in the hydrogen bond donors to sulfate and more solvent exposure of the ligand relative to the closed complex. Panel c and d summarize the binding pattern of the rank-order decoy, 10, which partitions into the more opened forms of GR (relative to compound 1); the FERM-SMD/Docking approach identifies and corrects the scores of these rank-order decoys, as described in the text.

4 Discussion

Presented here for the first time is a set of bona fide inhibitors of glutamate racemase (13 of the 17 ligands analyzed by FERM-SMD/Docking) spanning a large range of potencies and scaffolds. Especially interesting is the discovery of a unique family of sulfonate-containing aromatic compounds characterized best by 1, which has the lowest K_i (9 µM) of any GR inhibitor yet characterized. It is noteworthy that several studies have identified antibacterial and antifungal activity as well as the low toxicity of 1 (and derivatives thereof),^{[38, 39]} however the target and nature of the bioactivity were not determined. Compound 1 is one of our most promising leads for optimization, and thus it is essential that the structural moieties responsible for its relatively high affinity and ligand efficiency be clarified. Not surprisingly, Figure 1 indicates that rank-ordering, and thus logical structure based design is problematic without increased accuracy and precision in the prediction of binding free energies. Surmounting this barrier will facilitate the development of sorely-needed antibacterial therapeutics.

It has become clear that the main failure of docking for a flexible target, such as GR, is the gross assumption of a single representative structure for the receptor. Previous studies have reported the successful implementation of ensemble docking in virtual screening as a means of addressing receptor flexibility and improving enrichment and the accuracy of ligand placement.^{[2,7, 49]} This study aims at extending the reach of classical docking into the realm of affinity rank-ordering by enhancing target information (i.e., steered ensemble docking). The wide variety of programs and approaches for representing local receptor flexibility by using thermal sampling techniques mixed with classical scoring functions are not appropriate for solving the affinity rank-order problem. The authors are not aware of any published study in which such approaches are tested for the ability to rank-order validated sets of inhibitors.

The FERM-SMD/Docking approach represents receptor flexibility in an inexpensive manner by utilizing ensemble docking of SMD-derived structures, which when combined with solvation free energy calculations, corrects for previously inaccurate rank-ordering of ligands. This relatively inexpensive SMD simulation provides a much improved target (ensemble) than the single crystal structure used in orthodox docking and virtual screening. The improvement in Spearman correlation coefficient (R = 0.79) and precision (RMSE = 0.7 kcal/mol) due to the FERM-SMD/Docking, places this approach amongst the highest accuracy (as measured by rank-order correlation) methods that have been published. The best methods for achieving high accuracy and precision are mostly alchemical approaches (e.g., TI),^{[9,11, 44, 50, 51]} reaching R values in the range of 0.72 to 0.85 and RMSE values in the range of 0.4 kcal/mol to 0.7 kcal/mol. However, several studies achieved high accuracy (R > 0.7) using endpoint approaches (e.g., MM/GBSA^[15]), but these often had much lower precision than alchemical methods.^{[9, 15, 43, 45, 46]} Several authors have cited a 1 kcal/mol threshold value as having real benefits in the workflow of lead optimization.^{[9, 41]} However, the benefits of precise prediction of relative ligand affinities extend beyond simple synthetic convenience. This is especially true in the rapidly changing landscape of natural products synthesis, as recently reviewed by Li and Vederas.^[52] Currently, the intersection of drug discovery and natural products is characterized by great compound diversity and even greater synthetic expense, thus the importance of accurate rank-ordering goes beyond improvement of workflow and will most likely mean the difference between pursuit and abandonment of a candidate compound. Consequently, accuracy and precision is best achieved with either alchemical approaches or an efficient ensemble docking and scoring method, such as FERM-SMD or the Docking/MD/LIE of Stjernschantz and Oostenbrink (2010).^[16]

One recent and noteworthy study by Stjernschantz and Oostenbrink outlined the successful implementation of a hybrid docking and MD scheme that employs end-point Linear Interaction Energy (LIE) calculations for cytochrome P450 2C9.^[16] Under the assumption that a multitude of binding poses not only exist but each contribute to the overall binding affinity of a ligand to P450 C29, classical docking to a crystal structure was carried out and 4 pre-determined poses (of varying ligand orientation within the active site) were selected from the docking results. These select four complexes were then subjected to 2 ns of MD simulation and binding energy calculations via LIE. The correlation of predicted and experimental binding energies of a set of 12 ligands was improved significantly (R = 0.83, RMSE = 0.7 kcal/mol) over ChemScore alone (R = 0.55; the scoring function utilized by GOLD).^[16] This method is comparable in accuracy and precision to the scheme presented here but differs greatly in its computational requirement. Contrary to the FERM-SMD method, the method discussed above requires four individual MD simulations for each ligand. The FERM-SMD method uses approximately 50 ps production simulation time for the actual SMD, while alchemical methods often employ about 20 ns per ligand, depending on the number of λ values used per transformation, often resulting in hundreds of ns per entire ligand set.^[42]

Another study, by Colizzi et al.,^[53] recognizes that orthodox docking fails to represent the true binding energy of a congeneric set of β-hydroxyacyl-ACP dehydratase inhibitors. By exploiting the power of SMD to capture conformational states that are otherwise not sampled by classical MD, the method developed in this study correctly partitions inhibitors into “active” (IC₅₀ values in the low “M-range) and “inactive” compounds by comparing the force profiles produced from individual inhibitor-unbinding SMD simulations. Like the study conducted by Stjernschantz and Oostenbrink, this method requires individual MD simulations for each inhibitor, a more costly undertaking than the single SMD simulation required by FERM-SMD. Additionally, the method developed by Colizzi et al. has not yet demonstrated whether the generated force profiles have the resolution to allow for accurate rank-ordering of a set of ligands, only general partitioning of inhibitors that vary in potency by a factor of at least two orders of magnitude (ie. an enrichment study).

Currently, the FERM-SMD method is not without limitations. Primarily, the applicability of the method is limited by the ability to correctly represent unbinding in a steered molecular dynamics simulation. Specifically, correct sampling is essential to the accuracy of the subsequent docking and scoring. For this system, the pulling vector used in SMD was easily estimated (as should also be the case for other enzymes with buried active sites and a single substrate entrance/exit). However, in the case of enzymes with large, poorly-defined active sites, determining the correct pulling vector for an unbinding SMD is far less trivial. If the unbinding (or binding) trajectory is non-obvious, elucidation may be achieved by multiple exit vector SMD simulations, which may significantly reduce the efficiency of the improvement in accuracy. However, even this may be preferable to performing alchemical calculations on a large set of ligands. Additionally, at this time, FERM-SMD is not an accurate means of calculating absolute binding free energies. It should be noted that a variety of MD sampling approaches have been used to determine precise absolute free energies of binding for one or a few compounds,^{[50, 54, 55]} with errors of only 1 or 2 kcal/mol, but here we only consider comparisons of methods for accurate and precise determination of relative binding free energy from validated sets of inhibitors.

Mobley et al. suggested that it may be necessary to account for not only protein conformational changes alone, but also to determine the free energy differences associated with the conformational transitions in the receptor, in order to achieve free energy calculations with high accuracy.^[50] Indeed, FERM-SMD/Docking takes into account a correction based on estimated changes in the ΔG_{Solv,Receptor} between different structures of the ensemble, which are used to correct the docking score, where it is assumed that ΔG_{Solv,Receptor} is the dominant factor in free energy changes between structures in the ensemble. Thus, this parallels the predictions made by Mobley et al. that not only would one have to account for structural changes that occur in the target, but also to consider energetic changes that occur between such structures. However, it is surprising that a correction simply based on endpoint ΔG_{Solv,Receptor} using PB approaches would be sufficient to achieve the large enhancement seen in this study. This may be due to the accuracy of the AutoDock scoring function to predict ligand affinities (for binding to a single receptor structure, i.e., with no receptor flexibility), which includes empirically parameterized terms for ligand desolvation and entropy. Furthermore, the version of AutoDock used in this study (a module of the YASARA Structure package, YASARA Biosciences^[56]) employs a more sophisticated charge acquisition scheme than standard AutoDock packages, based on a semi-empirical quantum chemical RESP-like autoSMILES method.^[57,58]

In the future, it would be desirable to apply this method to other flexible enzyme targets in order to test the applicability of FERM-SMD/Docking across a range of enzyme classes as well as reveal any additional inadequacies or biases inherent to the system. As pointed out by Shirts et al., obtaining high-accuracy ligand binding data has been surprisingly problematic.^[9] However, the recently NIH-funded initiative, Community Structure-Activity Resource (CSAR),^[59] has begun to address this problem by curating high quality binding and structural data from previously proprietary pharmaceutical databases.

A hybrid Steered-MD-Docking procedure has been described, which corrects the rank ordering of a set of 17 inhibitors of the highly flexible, antimicrobial drug target, glutamate racemase. The current study employs this technique in the elucidation of binding determinants for a new class of sulfonate GR-inhibitors, best exemplified by 1, which was shown in this study to be a competitive inhibitor with a K_i of 9 µM. This hybrid SMD-Docking approach is shown to have high accuracy, precision and efficiency (i.e., improvement in R value per total simulation time), when compared to the many other methods that attempt to predict binding affinities for protein-ligand complexation.

Figure 5.

Correlation of binding free energies as predicted by FERM-SMD/Docking and experimental binding affinities from various inhibitor-GR complexes. FERMScore values are predicted using the FERM-SMD/Docking scheme described above. Experimental binding constants are approximates based on experimentally-derived K_M, K_i and IC₅₀ values. Data is fit to a semi-log regression and the Spearman correlation coefficient is noted. The ± 1 kcal/mol threshold is marked (dotted lines).

Scheme 1.

Representative compounds from a promising new class of GR inhibitors.