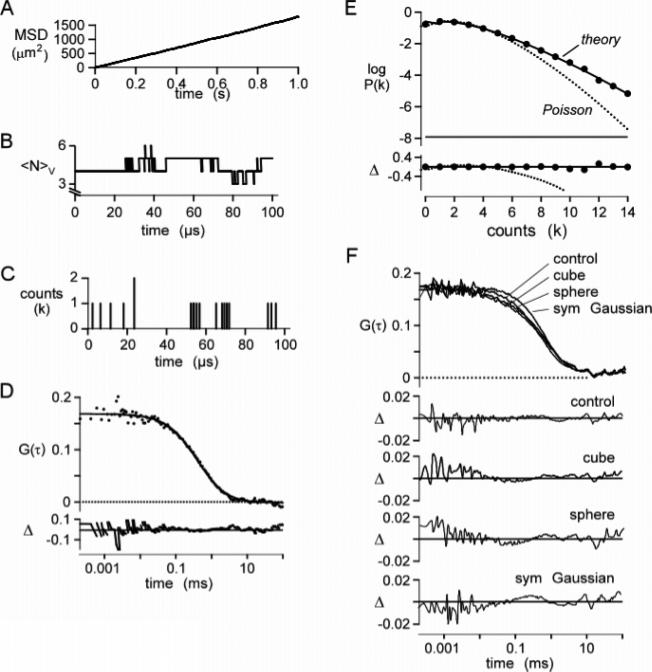
Figure 2.

Validation of simulation method. The Brownian dynamics simulation of particle diffusion was run for 1 s using a 200 ns time step for 1000 molecules with a diffusion coefficient of 300 μm²/s in a 10 × 10 × 10 μm³ box (average concentration 1 particle/μm³; 1.7 nM). (A) Mean-square displacement plot of particle positions. The fitted slope gives a diffusion coefficient of 298 μm²/s. (B) Representative plot of the number of particles, N_V, in a 1 × 1 × 3 μm³ cubic observation volume. (C) Corresponding plot for detected photons. Molecules were excited with a Gaussian excitation profile of w_xy = 0.354 μm, w_z = 1.061 μm (κ = 3), and specific brightness 17 kHz/molecule. (D) Autocorrelation function, G(τ), computed from F(t) from four separate simulations. The solid line is fitted G(τ) for a simple diffusion (eq 9) (see text for fitted parameters), with fractional deviation (Δ) shown in the lower panel. (E) Photon-count histogram, P(k;ΔT), generated from the fluorescence trace with ΔT = 20 μs. Data were fitted with the P(k;ΔT) for the Poisson distribution (dotted curve) and the super-Poissonian model (theory; solid curve) (Chen et al.¹²). (F) Effect of the excitation profile on G(τ). Trajectories were generated as above. The fluorescence module was modified to produce cubic, spherical, and symmetric Gaussian (ω_x = ω_y = ω_z) excitation profiles. Simulated data were fitted with eq 9, and the fractional deviation between fit and simulation (Δ) was plotted.