Simulation of Chaperonin Effect on Protein Folding: A Shift from Nucleation–Condensation to Framework Mechanism

Abstract

The iterative annealing mechanism (IAM) of chaperonin-assisted protein folding is explored in a framework of a well-established coarse-grained protein modeling tool, which enables the study of protein dynamics in a time-scale well beyond classical all-atom molecular mechanics. The chaperonin mechanism of action is simulated for two paradigm systems of protein folding, B domain of protein A (BdpA) and B1 domain of protein G (GB1), and compared to chaperonin-free simulations presented here for BdpA and recently published for GB1. The prediction of the BdpA transition state ensemble (TSE) is in perfect agreement with experimental findings. It is shown that periodic distortion of the polypeptide chains by hydrophobic chaperonin interactions can promote rapid folding and leads to a decrease in folding temperature. It is also demonstrated how chaperonin action prevents kinetically trapped conformations and modulates the observed folding mechanisms from nucleation–condensation to a more framework-like.

Introduction

Protein folding occurs in vivo in the environment quite unlike that under experimental, in vitro conditions. A large fraction of newly synthesized protein chains do not fold spontaneously, but are assisted by molecular chaperones.(1) Chaperonins, a class of hollow cylindrical chaperones, are responsible for binding and encapsulating substrate proteins (SP) in their non-native conformations by enabling them to reach their native states. The exact mechanism of chaperonin assistance in protein folding remains unsolved. The observation of protein dynamics in the presence of or inside the chaperonin by means of experimental techniques is extremely difficult and lacks sufficient detail.

A number of models have been proposed for the chaperonin mechanism related to either direction of the chaperonin cage role: passive (aggregation prevention without altering the folding mechanism or kinetics) or active (folding promotion).¹⁻³ The two major active models are iterative annealing mechanism (IAM), where the chaperonin promotes folding by unfolding from misfolding traps, and the active cage model exploring the role of the chaperonin interior microenvironment on SP folding promotion. There is evidence for either of these mechanisms, both experimental and theoretical, and none of them is mutually exclusive.(2) The presence of more than one mechanism may be important for the ability to serve a great variety of different SPs, which may require different supportive mechanisms.

Probably the earliest and most popular explanation of the chaperonin active role is the IAM model.^2,3 The first theoretically driven IAM concepts^4,5 were followed by simple kinetic models and simulations of chaperonin-assisted folding. The earliest simulations involved highly simplistic protein-like models and later less simplified real protein models, recently reviewed in refs (2,3).

The common interaction model for the chaperonin-assisted folding simulation of real proteins is the simplified potential known as the Go-model employed in most, if not all, simulation studies.(2) Go-like models favor native interactions, assuring the lowest energy for the native conformation a priori, and ignore non-native interactions, assuming their low importance in folding mechanisms. For many proteins, non-native interactions could be important as shown, for instance, in the B1 domain of protein G (GB1) folding studies.(6) In this respect, the present results differ from the other IAM models. The simulations presented here rely on the predictive power of the model, rather than on biasing the interactions toward the native ones. That is because the CABS force field, derived from statistical regularities seen in experimentally determined protein structures, describes molecular interactions common for all globular proteins, and not for a single structure as assumed in the Go-like models. Therefore, CABS simulations do not preclude different from “down the hill” folding pathways, as it has been demonstrated in our earlier work.

This work is a continuation of in silico studies of protein folding pathways by means of stochastic dynamics, coarse-grained representation, and knowledge-based potentials (the CABS model).^7,8 An overview of the CABS model is given in the Materials and Methods. The folding mechanisms observed in simulations (for the paradigm systems: chymotrypsin inhibitor 2 and barnase(7) or GB1(8)) showed high consistency with the experimental findings on the level of individual residues. In this work, we apply a similar strategy to characterize the equilibrium folding of B domain of protein A (BdpA). Next, a simple IAM chaperonin protocol is applied to BdpA and GB1 domains. Following one of the most popular theoretical pictures of the nonspecific mechanism of chaperonin action, it is assumed that the protein inside the chaperonin cage is subject to periodic swelling caused by hydrophobic interactions with the cage walls. Thus, the present simulations could be considered as a computational test of such an IAM model, describing its consequences on the molecular level, and thereby providing some additional hints for designing new experiments.

BdpA and GB1 are not natural chaperonin SPs as their small size and spontaneous, fast folding process make them very good folders. Importantly, their folding process is particularly well reproduced in the CABS model as we show here for BdpA and already described for GB1.(8) The CABS simulation of both proteins offers a possibility to observe multiple transitions from a highly denatured ensemble (perfectly matching experimental data) to a native-like ensemble, around 2 Å from the native, in a short time. Because the simulation accurately describes the ground and transition states, we expect correct prediction of the changes introduced by the chaperonin protocol.

Materials and Methods

Chaperonin Model

The simple chaperonin-like protocol was implemented within the CABS algorithm.(9) CABS proved very accurate in protein folding^7,8 and protein structure predictions (ranked as best, or one of the best, among other approaches in CASP6 blind prediction experiments).(10)

A detailed description of CABS, the CA-CB-side-chain protein modeling tool, can be found elsewhere.(9) Here, we provide a concise outline only of the most important features of this modeling tool. CABS coarse grained representation of polypeptide chains uses up to four united atoms per residue. These are α carbon, β carbon, a virtual united atom placed at the center of mass of a side group (where applicable), and a virtual atom placed in the center of the Cα–Cα virtual bond. The Cα-trace is restricted to a high resolution (0.61 Å spacing) cubic lattice. Allowing some fluctuations of the Cα–Cα distances leads to 800 possible orientations of Cα–Cα virtual bonds. Positions of the remaining united atoms are not restricted to the lattice, being defined in the local Cartesian coordinates determined by the Cα-trace. The lattice representation enables very fast computation of local conformational transitions, making CABS simulations about 100 times faster in respect to otherwise similar continuous models. The stochastic dynamics of the CABS chains is simulated as a long series of small conformational updates controlled by an appropriately designed (pseudo)random mechanism. Except for very short times (corresponding to the characteristic time of the local conformational transitions), the CABS Monte Carlo dynamics is equivalent to Brownian dynamics of analogous continuous space coarse-grained models.

The force field of CABS is knowledge-based, and the parameters of the constituent potentials are derived via Boltzmann inversion applied to the statistics of structural regularities seen in experimentally solved protein structures. The interaction scheme consists of sequence-dependent short-range conformational propensities, a model of main-chain hydrogen bonds, and context-dependent potential of pairwise interactions of side groups. The averaged solvent effect is accounted for in an implicit fashion in the statistics used in the derivation of the CABS potentials. Thus, at present, the model cannot be used for straightforward simulations of “atypical” pH or ionic strength effects on protein structure and dynamics. The average hydrophobic effects are well accounted for, and it has been proven that the model is capable of reproducing complex details of protein folding mechanisms.^7,8

We probed several versions of the chaperonin model. The sizes and shapes tested included spherical small (r = 2R_g), spherical medium (r = 2.33R_g), spherical large (r = 3R_g), and cylindrical (r = 2R_g) models, where r is the radius of a sphere or a tube (cylindrical) and R_g is the estimated, native radius of gyration of a given protein. During the hydrophobic disruption cycle (see below), the walls of the model chaperonin attract the polypeptide segments with a strength set to 1kT_B, and a thickness of the attractive wall equal to 1R_g. For each chaperonin model, we performed a set of long isothermal simulations at reduced temperatures from 2.52 to 2.90 for GB1 and 3.10 for BdpA with the 0.02 increment.

A single chaperonin cycle consisted of 10 time intervals of equal length. Only the first interval of a cycle refers to the chaperonin hydrophobic attraction phase; in the remaining nine intervals, the chaperone is inert with respect to the encapsulated protein (see also Figure 4A). Each run simulated 1000 chaperonin cycles, and each cycle lapsed with 20 000 arbitrary time units, where the time unit of Monte Carlo dynamics corresponded to several (range of 10) attempts at various local random micromodifications of the model chain per residue (see a detailed description of the CABS modeling tool). Because the sequence of local micromodifications is controlled by a pseudorandom mechanism, the evolution of the model chain follows a coarse-grained Brownian motion. Every simulation started from a random conformation prepared in a separate, short, high temperature run.

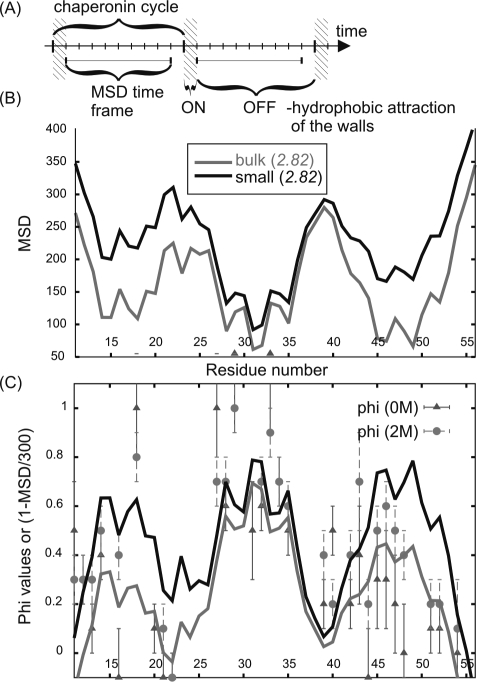
Figure 4.

Characterization of BdpA mobility and comparison with experimental Phi values. (A) Illustration of the chaperonin cycle and the time frame used for measuring chain mobility. (B) Profiles of the mean square displacement (MSD, measured in Ų) for BdpA bulk and small chaperonin simulations calculated for all of the simulation snapshots. (C) Comparison of residue mobility (plotted as: 1 – MSD/300) with phi values measured for 0 and 2 M GdmCl (denaturant) concentration (10).

Simulation Analysis

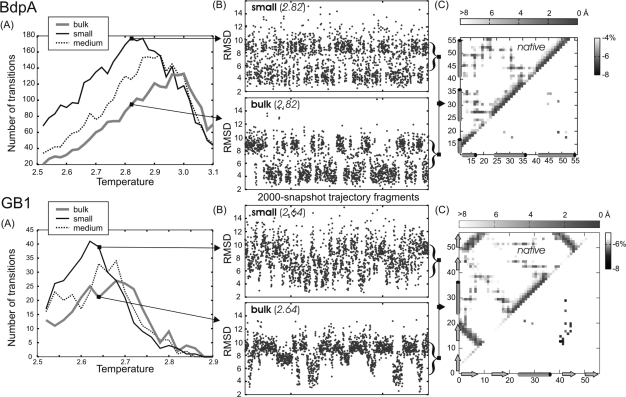
The number of folding transitions (Figure 3) was estimated as a number of transitions between low root-mean-square deviation (rmsd) structures (below 5 Å) and high rmsd structures (above 9 and 10 Å, for BdpA and GB1, respectively), using the averaged rmsd values over the trajectory frames spanning one-half of the chaperonin cycle.

Figure 3.

Summary of chaperonin and bulk simulations for BdpA and GB1. (A) Number of folding transitions between denatured and native-like ensembles, see also Materials and Methods, as a function of temperature. (B) The rmsd (from native) flowcharts at selected temperatures for small chaperonin and bulk systems. (C) Difference contact maps (below the diagonal) show the weakening of folding nuclei by the chaperonin (see the text). The maps were obtained by subtracting side-chain contact (7 Å cutoff) frequencies from chaperonin and corresponding (at the same temperature) bulk system simulations (preceded by the normalization over the number of TSE snapshots) and were shaded gray to show meaningful differences only. Native distance maps (above the diagonals) are given for reference.

TSE structures where defined as those having 5.5 < rmsd < 8.5 Å for BdpA, and 6 < rmsd < 9 Å for GB1, respectively. These TSEs contributed to about one-fourth of BdpA and one-half of GB1 trajectory snapshots (BdpA exhibits more two-state-like behavior).

Simulation analysis was done with a Bioshell tool-set–utility library for structural bioinformatics.^11,12

Secondary structure assignments (helix, strand, coil), presented in Table 1 and Figure 6, were done using the P-SEA algorithm.(13)

Table 1. Average BdpA Secondary Structure Content^a.

simulations at T = 2.82	all snapshots		most expanded only
helices content	bulk	small	bulk	small
H1	0.139	0.129	0.076	0.085
H2	0.666	0.654	0.563	0.571
H3	0.559	0.547	0.506	0.480

^aAverage number of residues with helix secondary structure assignment in the bulk and the small chaperonin simulations for all the trajectory snapshots (10 000 snapshots) and the most expanded only (with radius of gyration larger than 11 Å, constituting 5% of the bulk and 18% of chaperonin simulation).

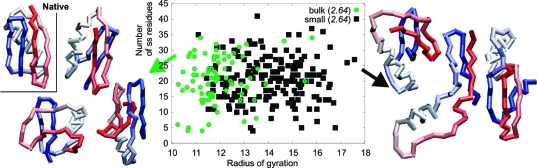
Figure 6.

Characteristics of the most misfolded GB1 structures from the bulk and chaperonin simulations. Plot of secondary structure content (number of residues assigned as helices or strands) in the most misfolded structures (rmsd > 12) against their radii of gyration (in Å) for the bulk simulations (green ● and example structures on the left) and small chaperonin (◼ and example structures on the right), respectively. Native structure of GB1 is given for reference.

Results

Simulation Design

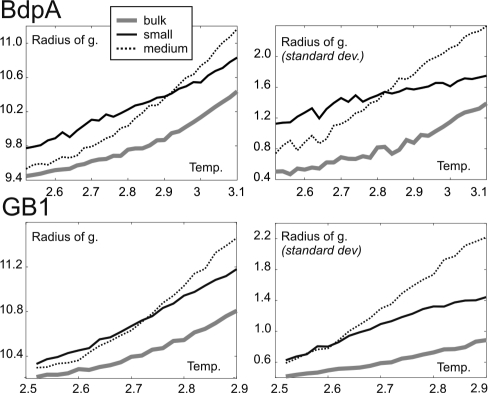
Chaperonin-assisted simulations of BdpA and GB1 were performed independently with several size and shape chaperonin types (see Materials and Methods) and compared to the results of equilibrium folding simulations for a protein only (bulk) model. Temperature-dependent compactness analysis (see Figure 1) and other characteristics showed the most significant impact for a small and a medium-size spherical chaperonin, and for clarity only these types are presented here.

Figure 1.

Temperature-dependent characteristics of BdpA and GB1 coil/globule dimensions. Mean radius of gyration (in Å) and its standard deviation as a function of reduced dimensionless temperature for two types of chaperonins (small and medium) as compared to chaperonin-free (bulk) simulations. Chaperonin-assisted simulations produce, on average, less compact structures, although with significantly larger structural variability.

Bulk BdpA Folding

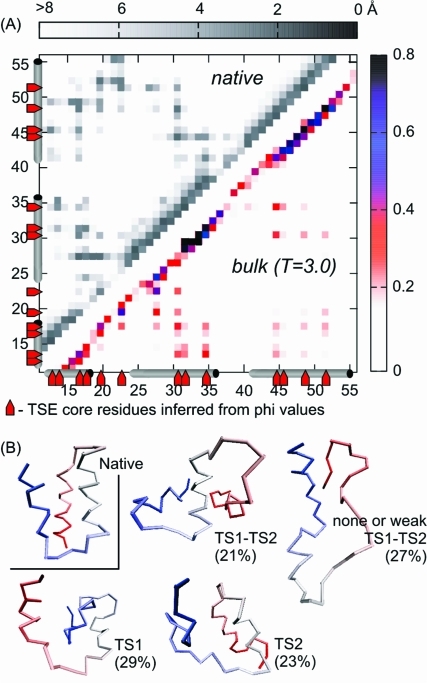
BdpA is a three-helical protein (PDB code: 1BDD), 46 residues long (when the N-terminal unstructured fragment is truncated), which folds according to simple two-state kinetics.(14) The folding pathway of BdpA is one of the most systematically studied by computer simulation because of the short folding time scale, close to current simulation capabilities. Not long ago, it was also thoroughly examined by the phi value analysis,(15) the only extensive experimental technique sufficiently close to atomic resolution. As experimentally assessed, many of the simulation predictions captured important folding features; however, none was entirely consistent with the experimental data, especially with respect to the observed order of folding events. As summarized by Wolynes,(16) the transition state ensemble (TSE) structures seen in simulations broadly fall into two classes, those suggesting an H1 and H2 helices dominant role,^17,18 and those highlighting an H3 helix role¹⁹⁻²⁴ and its interactions with H2. These inconsistencies may be due to the existence of multiple transition states and pathways of BdpA, as inferred from the statistical mechanical folding model(25) (discussed in more detail in the next section).

The phi value analysis suggested the following:(15) TSE is constructed around a nearly fully formed H2 stabilized by hydrophobic interactions with H1, which is only weakly structured. Some structure was noted within the turn connecting H2 and H3 and the N-terminus of H3. H3 was found to contribute to stabilizing hydrophobic interactions by its N-terminal side chains, while C-terminal interactions are less important. In general, the folding follows the nucleation–condensation mechanism with the secondary structure well formed (mainly H2) and with a stabilizing contribution of hydrophobic interactions.

The CABS energy landscape for BdpA seems to be the least rugged among the paradigm systems we have described so far.^7,8 The average picture of the transitional, between-the-basins (native and denatured) conformers is amazingly consistent with the phi value observations (see Figure 2A). The most persistent cluster of contacts, forming an unstable network of tertiary interactions (contact probability ≈ 0.2–0.3; involving 14 residues: 14, 15, 17, 18, 20, 23, 28, 31, 32, 35, 45, 46, 49, 52), belongs to the extended hydrophobic core identified in the phi value analysis (except for R28 and W15, for which phi values have not been estimated). The most persistent contacts were those between H1 and H2 with F14, L18, F31, I32, L35 playing a central role (and all having high phi values; see Table 3 in ref (15)). The next group (about 1/4 from the most persistent) are H2–H3 contacts, with L45 as the dominant H3 residue (the highest phi value among the H3 residues: 0.6) interacting most notably with F31 and L35 (also heavily involved in H1–H2 contacts). The rest of the most persistent ones are individual contacts of turn 1 (T1) with all of the helices and H1–H3 contacts formed mostly by L18, L45 and I13, A49, L52 (moderate phi values). Analyzing the secondary structure formation, the 31–35 region of H2 is the best structured thanks to the stabilizing tertiary interactions (see Figure 2), H3 does have some structure, and H1 is only weakly structured (see also the average secondary structure content in Table 1). Phi value analysis suggests a similar picture, although with a somewhat more stable H2 secondary structure and weaker H3. Interestingly, H3 early formation agrees with experimental measurements of isolated helices stability and the general picture emerging from the simulation studies.(16) Recently, a very detailed computational study of BdpA, using a different coarse-grained model of protein folding, UNRES, has been published.^26,27 The overall picture emerging from these studies is very similar to the findings of the present work. In particular, the identified set of residues responsible for nucleation of folding, the order of the secondary structure, and tertiary network formation are almost the same, despite qualitatively different philosophy and design of CABS and UNRES. UNRES is a continuous space model with its force field being physics-based (in contrast to the knowledge-based potentials of CABS) and classical molecular dynamics used in simulations. This provides yet additional justification of the applicability of knowledge-based models not only to structure prediction but also to the prediction of dynamics (folding/assembly pathways) of proteins.

Figure 2.

Structural characterization of BdpA transition state ensemble. (A) Averaged side-chain contact map (with 7 Å cutoff) of the BdpA nucleation core from bulk simulation at T = 3.0 (below the diagonal). The colors indicate the probability of contacts. Short-range contacts (up to i, i+3) are omitted for clarity. Native distance map (above the diagonal) is shown in gray scale, indicating pairwise distances. Native helices and extended hydrophobic core residues in the TSE, inferred from phi value analysis,(15) are marked at the borders of the map. (B) Examples of BdpA TSE structures (percentages are explained in Table 2) as compared to the native.

BdpA Folding: Chaperonin Model

The highest frequency of interconversions between native-like and denatured ensembles is observed for the small chaperonin (see Figure 3A). Therefore, the small variant was chosen for more detailed analysis (Figure 3B,C). The time-averaged side-chain contact maps from the chaperonin and the bulk system were used to calculate difference contact maps (see Figure 3C). The most pronounced differences were observed at chaperonin maximum yields (T = 2.62; 2.64; 2.66) and indicated the weakening of the folding nucleus, most significant in the key contacts between H2–H3 (L45 with F31, L35, the most distinct at T = 2.64, and A49–F31) together with individual contacts between H3 (L52, A49) and H1 (I18) or T1 (L20). This suggests a chaperonin-induced shift toward a nucleus centered more on H1–H2 than on H2–H3.

To measure protein chain mobility, the autocorrelation function (time-averaged mean-square displacement, MSD) was calculated as a function of time lapse and residue position in the sequence (Figure 4) according to the following formula: MSD = g(Δt) = ⟨(r_i(t + Δt) – r_i(t))² ⟩ where r_i(t) are Cartesian coordinates (in angstroms) of the ith side chain at time t, and ⟨⟩ denotes averaging over a long trajectory. Time is measured by the number of steps of the CABS stochastic dynamics.

The mobility profiles correlate well with the phi values. It means that on the microscopic level the experimental phi values measure not only the structural stability in the neighborhood of selected residues (see the correlation of the high phi values with frequency of ternary contacts during the folding demonstrated in Figure 2A) but also the residues’ local mobility along the folding pathways. As demonstrated in Figure 4C, where the mobility profiles are arbitrarily rescaled using a linear function, high phi values imply low mobility, and vice versa. Mobility analysis shows that the chaperonin action significantly alters H1 and H3 (with H3 being slightly more stable). Thus, more efficient sampling of H1 and H3 around the folding nucleus center (H2) occurs, and H2 remains the most stable region under the chaperonin disruption cycles. Interestingly, the calculations of time-averaged secondary structure content show slight additional stabilization of H1 and H2 in the most expanded structures, as compared to bulk folding (Table 1).

According to the statistical mechanical model of folding analysis,(25) the BdpA nucleation process can proceed through many pathways, and most of them should pass through two distinct TSEs: centered at H1–H2 or H2–H3 (TS1 and TS2, respectively). Moreover, the TSEs and pathways are sensitively dependent on temperature and denaturant concentration, which may be the key to resolving the inconsistency among simulation and experiment (thus, comparing simulation and experiment, one has to ensure that they are conducted in the same conditions). The effect is a consequence of broken symmetry pathways in a nearly symmetrical protein: the TS1 interface involves a larger number of native interactions than that of TS2, which makes TS1 more sensitive to weakening upon denaturant addition or temperature increase. Itoh and Sasai(25) showed that under physiological conditions, BdpA should fold through TS1, while at high temperature and high denaturant concentration, pathways passing TS2s are more important. Consequently, the prediction of phi values in the unfolding process for high denaturant concentration(25) showed higher values in H3, low in H1, and highest in H2.

Contrary to the denaturing environment effect, the IAM employed here leads to TS2 rather than TS1 pathway destabilization as compared to the bulk system, which is not surprising as the environmental conditions remain the same and TS1 involves more contacts. The IAM and temperature-induced folding pathway modulation is quantified in Table 2. The changes are small, on the border of statistical significance, although the overall destabilization of the pathways involving either of the two transition states typical for the bulk folding is significant, as evidenced by the statistics given in column 2 of Table 2 (31% pathways seen in the chaperonin-assisted folding simulations do not pass through any of the well-defined transition states of the bulk folding).

Table 2. Temperature and Chaperonin-Induced Modulation of BdpA Folding Pathway^a.

model (temperature)	TS1 and TS2	TS1 and TS2 none or weak	TS1	TS2
bulk (3.0)b	21%	27%	29%	23%
bulk (2.82)*	23%	24%	30%	23%
small (2.82)*	18%	31%	30%	21%

^aThe modulation is shown by the percentage of four kinds of TSE structures for which TS1 and TS2 are well formed, or none of them, or TS1 only, or TS2 only. TSE structures were parsed as TS1 or TS2 well-formed if the number of long-range side-chain contacts within TS1 or TS2, native or non-native, was above an average from the entire simulation (measured in the bulk and given temperature). The average number of contact threshold values were 9.3 ± 3.1* (TS1), 6.1 ± 2.5 (TS2) at T = 3.0 and 10.6 ± 3.3* (TS1), 6.4 ± 2.5 (TS2) at T = 2.82 (*note that the TS1 threshold is much larger at lower temperature).

^bStructure examples are shown in Figure 2B.

GB1 Folding: Chaperonin Model

GB1 is a 56 residue, α/β protein (α-helix tightly packed against four-stranded β-sheet, PDB code: 2GB1). Recently, using the same ab initio modeling approach as here, we described its folding process in detail.(8) Interestingly, the simulations clearly showed a subset of native interactions driving the nucleation–condensation process from highly expanded conformations, with the observed folding nucleus perfectly matching the experimental data.

As compared with the bulk system, simulations within the chaperonin-like protocol produced notably more-expanded structures with a higher level of size and compactness variability, similarly to BdpA (see Figure 1).

As in the case of BdpA, chaperonin-mediated iterative unfolding leads to GB1 destabilization and temperature decrease where the largest number of transitions is observed (see Figure 3). Because the frequency of transitions should be the largest near the folding temperature, this indicated a decrease of the folding temperature, evident also from the observed shift of the heat capacity peaks (not displayed here). The result is contrary to the simulation of the confinement effect only for GB1 (and other SPs) folding showing significant SP stabilization and increase in denaturation temperature.(28) As can be seen in Figure 5, the chaperonin action leads to a more diffuse and less cooperative transition as compared to the simulation in the bulk. The native and unfolded basins are less separated (shallow near-native and unfolded basins) during the chaperonin-assisted folding.

Figure 5.

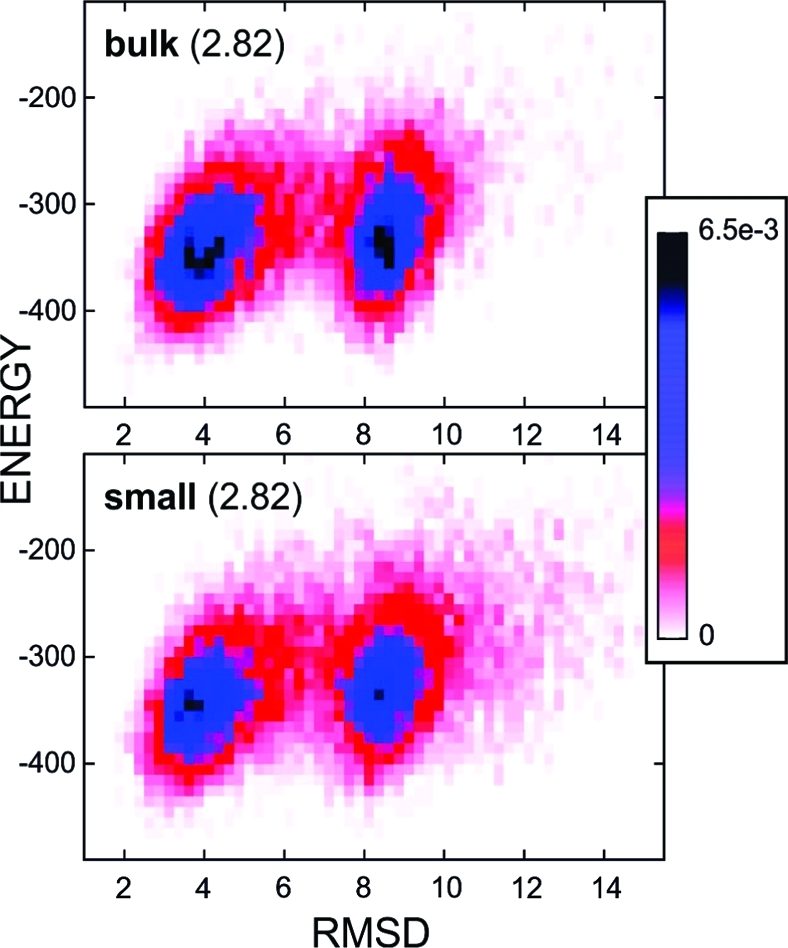
Distribution of structures according to their energy (CABS model) and rmsd values for the bulk system (upper panel) and small chaperonin (lower panel). Histograms were calculated at the same temperature (2.82), for all simulation snapshots (10 000), with bin sizes of 10 for energy and 0.25 for rmsd values. Colors denote frequencies of occurrence from black (6.5 × 10^–3), through blue and red, to white (0).

The maximum number of transitions for the small spherical chaperonin type is almost twice as high as in the bulk, as in the BdpA case. As seen in trajectory fragments shown in Figure 3B, GB1 two-state behavior is much less pronounced than for BdpA (reflected also in a nearly 5-fold difference in the maximum number of transitions for the same simulation length).

On the residue contact level, the most relevant difference between the bulk and the chaperonin system appears to be where the largest difference in transition yields occurs (T = 2.64). Given the relevancy criteria, no difference is observed in other temperatures. As seen in Figure 3C, chaperonin-mediated simulation differs almost exclusively in a smaller number of non-native β2−β3 interactions (being in the native at the edges of the 4-stranded β sheet) together with a notable decrease in F30–W43 contacts, belonging to the folding nucleus (the same at T = 2.62). Going down with the relevancy cutoff (applied in Figure 3), we observed an interesting feature at T = 2.62: one of the largest drops in the contact number (about −6%) for F30–W43 is accompanied by the largest increase (about 3%) for another folding nucleus contact, L5–W30 (together with other drops: notable in native-like β3−β4 contacts, less significant in β2−β3, and minor increase for native-like β1−β2). In summary, the observed nucleation mechanism appears to be similar to that in the bulk, but the sequence of events in the nucleation process is less emphasized; nucleus growth is more simultaneous.

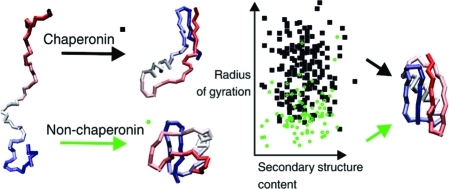
We also examined all of the structures with the least resemblance to the native, the misfolders (see Figure 6). The misfolders from the bulk and the chaperonin system have similar secondary structure content; however, some of the bulk are notably more compact, reaching an radius of gyration (R_g) of the native structure (10.8 Å) or even slightly smaller. Most of those densely packed misfolders have secondary structure patterns similar to the native but with secondary structure elements assembled in non-native supersecondary configurations.

Discussion

So far, the simulation studies of the IAM suggested essentially the same mechanistic concept: binding to the hydrophobic walls of the open chaperonin helps to pull out kinetically trapped SPs from their misfolded conformations.(2) We demonstrate that periodical disrupting can also have an effect on a folding pathway modulation toward the more efficient exploration of the folding landscape and avoiding the kinetic traps. The iterative relaxation of the tertiary structure together with stabilization of the preformed secondary structure elements results in the folding mechanism shifted from nucleation–condensation toward the framework. The shift of the folding mechanism manifests itself by a similar secondary structure content with and without a chaperonin effect (see Table 1 and Figure 6, confirmed also by rmsd of the native measurements of single BdpA helices) accompanied by the chaperonin-induced increased volume of structures and significantly larger structural variability (see Figures 1, 4, and 6). When taken at face value, the changes in the secondary structure alone suggest a slight shift toward the framework-like mechanism (Table 1); however, the small differences observed are statistically insignificant. Our observations remain in agreement with recent experimental evidence on chaperonin bound SP structure and indicate an ensemble of compact and locally expanded states which lack stable tertiary interactions.²⁹⁻³¹

Framework and nucleation–-condensation mechanisms of protein folding are extreme manifestations of an underlying common mechanism.^32,33 The former is favored by a highly stable secondary structure, while the latter is the concomitant secondary and tertiary structure formation. A shift between the two extremes is not unusual upon condition changes or even by a single mutation.^32,33

More generally, our results illustrate the power of the reduced protein models of interactions, motion, and chain representation employed. Combining experiment and simulation has already become a powerful method for describing protein folding pathways(33) and atomic details involved in the dynamic processes of macromolecular machines.(34) The future of accessing most of the molecular machineries of life would require new tools combining all-atom and coarse-grained schemes.³⁵⁻³⁸