Self-similar pulse evolution in an all-normal-dispersion laser

Abstract

Parabolic amplifier similaritons are observed inside a normal-dispersion laser. The self-similar pulse is a local nonlinear attractor in the gain segment of the oscillator. The evolution in the laser exhibits large (20 times) spectral breathing, and the pulse chirp is less than the group-velocity dispersion of the cavity. All of these features are consistent with numerical simulations. The amplifier similariton evolution also yields practical features such as parabolic output pulses with high energies, and the shortest pulses to date from a normal-dispersion laser.

Mode-locked fiber lasers have generated major interest as an alternative to solid-state systems owing to improved simplicity, stability and cost. From a purely scientific point of view, optical fibers and fiber lasers provide convenient and reproducible experimental settings for the study of a variety of nonlinear dynamical processes. Despite substantial research in this field, qualitatively new phenomena are still being discovered. Short-pulse fiber lasers based on soliton formation in anomalous-dispersion cavities [1], dispersion-managed solitons in cavities with a dispersion map [2], and all-normal-dispersion (ANDi) cavities [3–5] have been demonstrated. The latter system supports dissipative solitons in the cavity [6], and allows performance comparable to solid-state lasers [7]. In addition, ANDi designs allow for simple instruments at a lasing wavelength of 1 μm, an ideal wavelength for optical bandwidth and efficiency.

Self-similar pulses (“similaritons”) are parabolic pulses that convert nonlinear phase into a linear frequency chirp that can be compensated with standard dispersive devices. Specifically, similaritons are solutions of the nonlinear Schrodinger equation with gain,

$$\frac{\partial A}{\partial z}=\frac{g}{2}A-i\frac{{\beta }_2}{2}\frac{{\partial }^{2}A}{\partial t^2}+i\gamma ({\mid A\mid }^2)A,$$ (1)

with the form

$$A(z,t)=A_0(z)\sqrt{1-{(t/t_0(z))}^2}{e}^{i(a(z)-{bt}^2)}$$ (2)

for t ≤ t₀(z). Similaritons were first demonstrated theoretically and experimentally in single-pass fiber amplifiers [8–10], and they continue to attract much attention [11]. Self-similar evolution of a pulse in the passive fiber of a laser has been observed, and leads to major performance increases in pulse energy over previously-studied evolutions [12].

Solitons in passive fiber and self-similar pulses in fiber amplifiers are the most well-known classes of nonlinear attractors for pulse propagation in optical fiber, so they take on major fundamental importance. Solitons are static solutions of the nonlinear Schrodinger equation, and are therefore naturally amenable to systems with feedback. The demonstration of a laser that supports similaritons in its amplifier would be remarkable as a feedback system with a local nonlinear attractor that is not a static solution. The spectrum of the self-similar pulse broadens with propagation, so an immediate challenge is the need to compensate this in a laser cavity. A design with a long normal-dispersion gain fiber, a filter, and a linear anomalous-dispersion segment was proposed [13], but has not been realized experimentally. Oktem et al. reported a major step forward in this context: a laser with similariton evolution in the amplifier and soliton evolution in an anomalous-dispersion segment [14]. The soliton formation is thought to stabilize the similariton solution. Thus, self-similar pulse evolution has been observed only in lasers with dispersion maps. An unanswered question is whether amplifier similaritons can form in an ANDi laser, where satisfying the periodic boundary condition will be much more challenging. Such a pulse evolution would isolate the amplifier similariton in a system with feedback. Dissipation presumably would be a crucial process in that evolution.

Here we demonstrate self-similar pulse formation in the amplifier of an ANDi laser. Theory and experiments show that a range of inputs to the amplifier evolve to the self-similar solution, which verifies the existence of the nonlinear attractor in that segment of the oscillator. This local nonlinear attractor suppresses effects from the average cavity parameters that are unavoidable in lasers with dispersion maps. The solutions exhibit large (up to 20 times) spectral breathing, but the pulse chirp is always less than expected from the cavity dispersion. This new pulse evolution can be obtained over a broad range of parameters, which allows tuning the pulse duration, bandwidth, and chirp. For example, amplifier similaritons underlie the generation of the shortest parabolic pulses to date from a laser, in addition to the shortest pulses from any ANDi laser. The ability to generate high-energy chirped parabolic pulses or ultrashort pulses from a simple device will be attractive for applications.

Numerical modeling illustrates the main features of a laser that can support amplifier similaritons, indicated schematically at the top of Fig. 1(a). A gain fiber with normal group-velocity dispersion (GVD) dominates the parabolic pulse shaping. This is followed by a saturable absorber, which is assumed to be conversion of nonlinear polarization evolution (NPE) into amplitude modulation in the standard way. The cavity is a ring: after the filter, the pulse returns to the gain fiber. Propagation in the gain fiber, neglecting modal birefringence, is modeled with the coupled equations for the orthogonal electric field polarization states, A_x and A_y:

$$\begin{array}{l}\frac{\partial A_x}{\partial z}=\frac{g}{2}{A}_x-i\frac{{\beta }_2}{2}\frac{{\partial }^2{A}_x}{\partial t^2}+i\gamma ({\mid A_x\mid }^2+\frac{2}{3}{\mid A_y\mid }^2)A_x\\ \frac{\partial A_y}{\partial z}=\frac{g}{2}{A}_y-i\frac{{\beta }_2}{2}\frac{{\partial }^2{A}_y}{\partial t^2}+i\gamma ({\mid A_y\mid }^2+\frac{2}{3}{\mid A_x\mid }^2)A_y,\end{array}$$ (3)

where z is the propagation coordinate, t is the local time, β₂ = 23 fs²/mm is the group-velocity dispersion, and γ = 0.0044 (W m)⁻¹ is the cubic self-focusing nonlinear coefficient for the fiber. The linear gain coefficient is defined as:

$$g=\frac{g_0}{1+\frac{\int [{\mid A_x\mid }^2+{\mid A_y\mid }^2]dt}{E_{\mathit{sat}}}},$$ (4)

where g₀ = 6.9 is the small-signal gain corresponding to a ~30 dB fiber amplifier, E_sat = 170 pJ is the saturation energy, and the integral is calculated before propagation through the 2-m gain fiber. The polarization-dependent elements are treated with a standard Jones matrix formalism in the (x,y) basis. The NPE is implemented with a half-wave and a quarter-wave plate, a polarizer, and another quarter-wave plate, with orientations (with respect to the x-axis) θ_q1 = 2.21 rads, θ_h = 2.28 rads, θ_pol = π/2, and θ_q2 = 0.59 rads, respectively. The filter is a Gaussian transfer function with 4-nm full-width at half-maximum (FWHM) bandwidth. Finally, as in a practical oscillator a linear loss of 70% is imposed after the filter. The initial field is white noise, and the model is solved with a standard symmetric split-step algorithm.

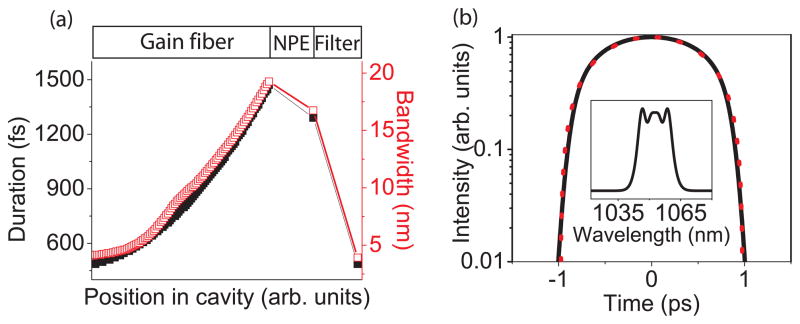
FIG. 1.

(a) Evolution of the FWHM pulse duration (filled) and spectral bandwidth (open) in the cavity. The components of the laser are shown above the graphs. (b) The output pulse at the end of the gain fiber (solid) and a parabolic pulse with the same energy and peak power (dotted). Inset: spectrum. The orthogonally polarized pulse and spectrum (not shown) are essentially identical.

A typical stable evolution is shown in Fig. 1(a). The two polarization modes evolve almost identically, so the sums of the temporal and spectral intensities are plotted. The pulse duration and bandwidth increase in the gain fiber as the pulse evolves toward the asymptotic attracting solution in the fiber. The filter and saturable absorber reverse these changes. The filter provides the dominant mechanism for seeding the self-similar evolution in the amplifier. This implies that only the initial pulse profile is important, and no additional nonlinear attraction is required, in contrast to soliton evolution in the results of Oktem et al.. Dissipative solitons and dispersion-managed parabolic pulses [12] have nearly constant bandwidth, and the pulse duration increases due to the accumulation of linear phase. In contrast, the amplifier similariton increases in duration as a consequence of its increase in bandwidth, which is an intrinsic property of the exact asymptotic solution [8]. A key feature of amplifier similaritons is that the pulses evolve toward a parabolic asymptotic solution: each polarization component is parabolic at the end of the gain fiber (Fig. 1(b)). The associated spectra exhibit some structure, as expected for a parabola with finite chirp (Fig. 1(b) inset). No stable solution was found with a single-field equation and a saturable absorber with transmission that increases monotonically with intensity; the coupling of the polarizations evidently provides some stabilizing function.

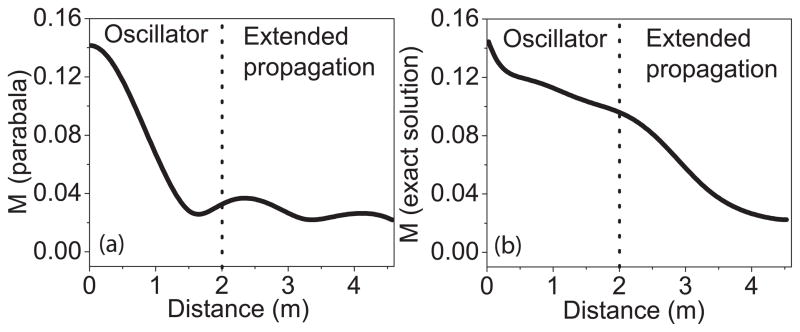
The pulse evolution can be quantified with the metric, M² = ∫[|u| − |p|]²dt/∫|u|⁴dt, where u is the pulse being evaluated and p is a parabola with the same energy and peak power. In the gain fiber, the pulse evolves from a Gaussian profile (M=0.14) after the spectral filter to a parabola (Fig. 2(a)). To verify that the pulse is converging to a parabola, the pulse at the end of the 2-m gain fiber is taken as the initial condition for propagation through an additional 3 m of identical gain fiber, and the pulse remains parabolic (Fig. 2(a)). To further confirm that the pulse is converging to the exact asymptotic solution demonstrated in Refs. [8–10], p from the M² metric is replaced with the pulse representing the asymptotic solution for this fiber. Indeed the pulse evolves toward the attractor in the gain fiber (Fig. 2(b)). The resulting pulses exhibit a parabolic shape and large spectral breathing as is expected from the parabolic attractor. The numerical simulations clearly show the formation of the amplifier similariton inside the laser.

FIG. 2.

Evolution of the (a) M parameter comparing the pulse to a parabola and the (b) M parameter comparing the pulse to the exact solution of Ref. [8] in the oscillator. An additional 3 m of propagation was added to each plot to emphasize convergence.

We designed a Yb fiber laser with parameters similar to those of the simulations. The schematic is identical to dissipative soliton lasers ([6]) with the exception of a diffraction grating (300 lines per millimeter) placed before a collimator, which replaces the birefringent plate as a spectral filter. The wavelength-dependent diffraction along with the Gaussian dependence of the fiber acceptance angle yield a 4-nm Gaussian spectral filter when the collimator is 11 cm from the grating. Along with the three wave-plates required for NPE, we add a half-wave plate before the grating to optimize the transmission. The zeroth-order grating reflection is used as a secondary output for analysis. The Yb-doped double-clad gain fiber is 1.8 m long and is pumped with a multi-mode pump diode. 28 cm of single-mode fiber (a collimator pigtail) precedes the gain fiber and a pump/signal combiner and collimator follow it, which together add 128 cm of SMF. All fibers have normal GVD.

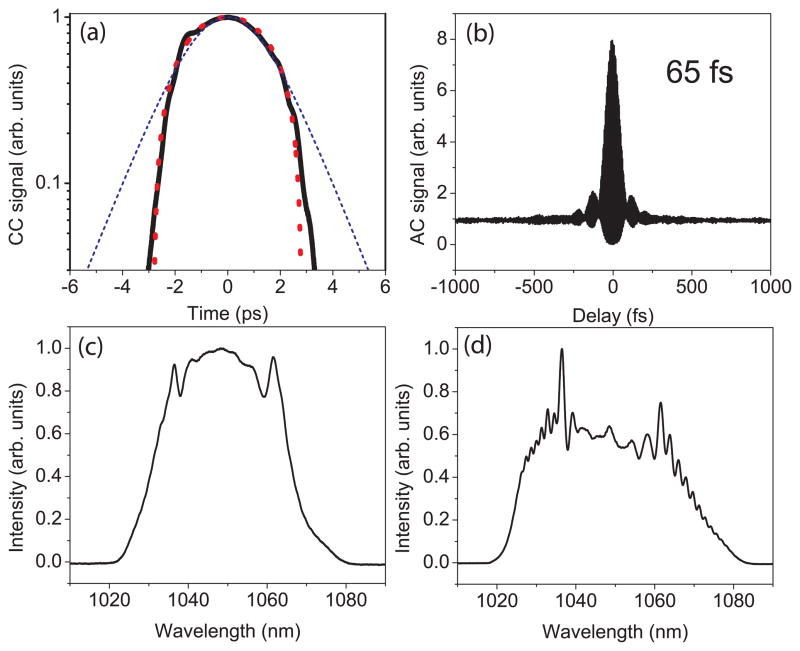
Self-starting mode-locking is achieved by adjustment of the wave plates. The chirped pulse from the grating reflection is measured directly by cross-correlation with the dechirped pulse from the NPE output, which is 60 times shorter than the chirped pulse (Fig. 3(a)). The pulse is parabolic and the spectrum (Fig. 3(c)) agrees well with the theoretical prediction for an amplifier similariton (Fig 1(b), inset). The shape of the spectrum is an immediate indication that this is a new regime of modelocking, as it lacks the characteristic steep edges of dissipative solitons in normal-dispersion lasers [4, 6]. The spectral bandwidth breathes by a factor of ~10 as the pulse traverses the cavity. The pulse from the NPE output (Fig. 3(d)) can be dechirped to a duration of 65 fs (Fig. 3(b)), with minimal secondary structure. The pulse chirp (0.05 ps²), inferred from the dispersion required to dechirp it to the transform limit, is less than the GVD of the cavity (0.08 ps²). This is another feature of this regime, as prior ANDi lasers have generated pulses with chirp comparable to, or much greater than, the cavity GVD.

FIG. 3.

Experimental (a) cross-correlation of the pulse from the grating reflection (solid) with a parabolic (dotted) and sech² (dashed) fit; (b) interferometric auto-correlation of the dechirped pulse from the NPE output; and spectra from the (c) grating reflection and (d) NPE output.

The narrow filter is crucial for the formation of similaritons in the amplifier. The challenge is for the pulse to reach the asymptotic solution in a fiber length that is compatible with efficient laser design. We offer the following argument: for fixed chirp, a pulse with a narrower spectrum is shorter and closer to the transform limit; such a pulse can reach the single-pass amplifier similariton solution in a shorter segment of gain. A pulse propagating in normal-dispersion gain fiber will always be attracted to the similariton solution, but if the pulse is too long, the effect is negligible and the resulting pulse will not be parabolic.

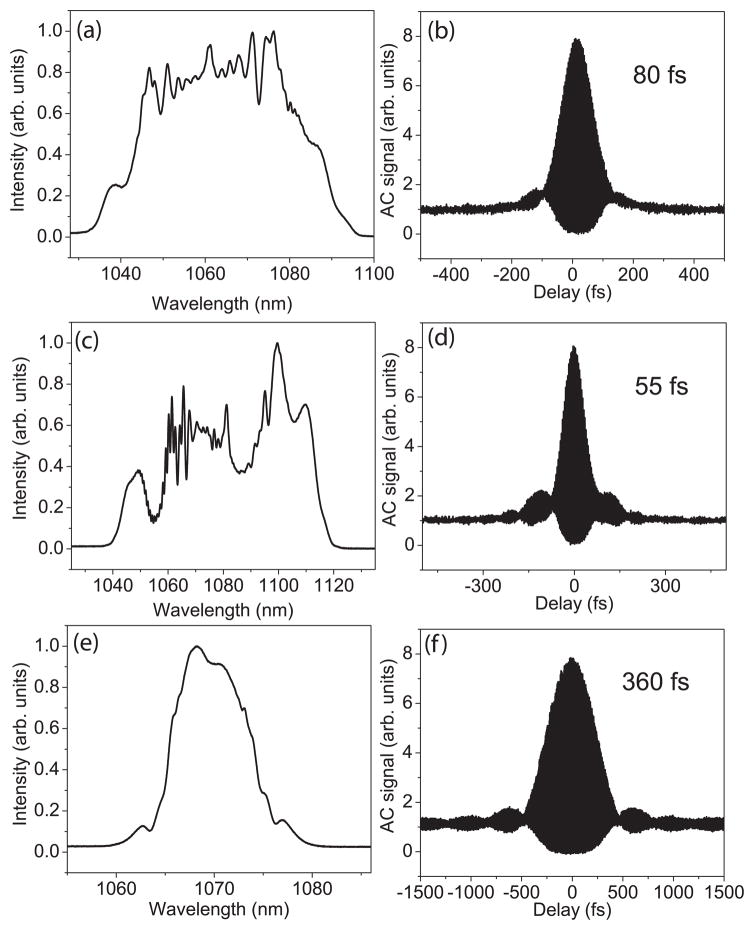
In contrast to prior pulsed lasers, the local attraction of the pulse to the amplifier similariton solution decouples the output pulse from other elements of the cavity. This property allows a variety of pulse evolutions and performance parameters. For example, with a narrower (2 nm) spectral filter, the pulse still evolves to an amplifier similariton with large bandwidth. The resulting solution has a very large spectral breathing ratio (~20), and yields 5-nJ pulses that dechirp to 80 fs (Fig. 4(a,b)). A well-known limitation to similaritons in fiber amplifiers is the gain bandwidth; as the spectrum approaches the gain bandwidth the chirp is no longer monotonic, which disrupts the self-similar evolution. With larger pump powers the spectral bandwidth increases, but the pulse quality is degraded. For example, with a 4-nm filter a 3-nJ pulse dechirps to 55 fs (Fig. 4(c,d)), a remarkably short pulse considering the large normal GVD of the cavity. Finally, amplifier similariton mode-locking is possible even with the addition of long lengths of fiber before the gain. For example, with 63 m of fiber and a 2-nm spectral filter, a 15-nJ pulse that can be dechirped to 360 fs is generated (Fig. 4(e,f)). These results extend the performance of recently-developed giant-chirp oscillators [15] to shorter pulses, which is needed.

FIG. 4.

Output spectrum and dechirped auto-correlation for modes with (a,b) large spectral breathing, (c,d) short pulse duration, and (e,f) long cavities.

The phenomena described here can be distinguished clearly from other pulse-propagation regimes. The pulses in Ref. [12] are self-similar in the passive fiber. The laser requires a dispersion-managed cavity and spectral filtering is avoided as much as possible. The spectrum of the passive similariton has characteristic steep sides, with minimal breathing. The passive similariton is not a nonlinear attractor, so there is no local attractor and the average cavity parameters influence the pulse evolution. Finally, parabolic self-similar mode-locking as in Ref. [12] was found to exist for a narrow region of parameter space [16]. All of these features contrast with the observations presented above for the amplifier similariton laser. Of course, dissipative solitons can be generated in a laser with only normal dispersion and a filter, as is the case here. However, dissipative solitons are characterized by a small spectral breathing ratio (<5), and the pulses are not parabolic [6]. Furthermore, the multi-pulsing threshold decreases with decreasing filter band-width, which severely restricts the stable mode-locking states that can be accessed with a narrow filter. The amplifier similariton regime allows much higher pulse energies and much shorter pulse durations to be obtained with the narrow filter. Giant-chirp oscillators are possible based on dissipative solitons [15]. These employ larger-bandwidth filters, so spectral breathing is small. The pulses exhibit the steep-sided spectra that are characteristic of dissipative solitons, and acquire frequency chirps that can be many times larger than expected from the cavity dispersion, again all in contrast to the long-cavity results of Fig. 4(e,f) above. Finally, the pulses in Ref. [14] are characterized by soliton evolution in an anomalous dispersion section of fiber. This requires dispersion management and fiber with anomalous dispersion in the cavity, which can limit the efficiency and simplicity of the operating regime. In contrast, similaritons in an ANDi fiber laser are stabilized with only a filter, which allows for a simple design with minimal components and without restriction on the lasing wavelength.

In summary, we have demonstrated self-similar pulse propagation in the gain segment of a normal-dispersion fiber laser. Strong spectral filtering is adequate to satisfy the periodic boundary condition of the laser. Thus, the evolution is dominated by the presence of the local nonlinear attractor in the cavity. This regime offers flexibility to design for distinct performance parameters. These include the shortest pulses generated by an ANDi laser and pulses with small and linear chirp, both of which will be valuable for applications.