Application of Polychromatic µCT for Mineral Density Determination

Abstract

Accurate assessment of mineral density (MD) provides information critical to the understanding of mineralization processes of calcified tissues, including bones and teeth. High-resolution three-dimensional assessment of the MD of teeth has been demonstrated by relatively inaccessible synchrotron radiation microcomputed tomography (SRµCT). While conventional desktop µCT (CµCT) technology is widely available, polychromatic source and cone-shaped beam geometry confound MD assessment. Recently, considerable attention has been given to optimizing quantitative data from CµCT systems with polychromatic x-ray sources. In this review, we focus on the approaches that minimize inaccuracies arising from beam hardening, in particular, beam filtration during the scan, beam-hardening correction during reconstruction, and mineral density calibration. Filtration along with lowest possible source voltage results in a narrow and near-single-peak spectrum, favoring high contrast and minimal beam-hardening artifacts. More effective beam monochromatization approaches are described. We also examine the significance of beam-hardening correction in determining the accuracy of mineral density estimation. In addition, standards for the calibration of reconstructed grey-scale attenuation values against MD, including K₂PHO₄ liquid phantom, and polymer-hydroxyapatite (HA) and solid hydroxyapatite (HA) phantoms, are discussed.

Introduction

Knowledge of mineral distribution in calcified tissues is of considerable importance. Laboratory studies have found the degree of mineralization to be a determinant of bone strength and fracture risk (Follet et al., 2004). Mineral density has also been considered as a standard parameter for the determination of demineralization and remineralization in dental caries, and thereby provides insight into the dynamic changes associated with the three-dimensional spatial distribution pattern of mineral within caries lesions.

There are numerous methods available for the evaluation of mineral concentrations in calcified tissues, each with its own advantages and disadvantages (ten Bosch and Angmar-Månsson, 1991; Arends and ten Bosch, 1992; White et al., 1992). The most direct is chemical analysis based on a known volume or mass (Elliott et al., 1998). Other techniques that have been applied for the assessment of mineralization include: scanning electron microscopy (SEM) (Johnson et al., 1969; Daculsi et al., 1979) and backscatter SEM (Roschger et al., 1998; Angker et al., 2004), confocal laser scanning microscopy (van der Veen and ten Bosch, 1996), chemical analysis (Arends and ten Bosch, 1992), and Fourier transformed infrared spectroscopy (Paschalis et al., 1997; Verdelis et al., 2003). These approaches require destructive specimen preparation (e.g., sectioning, milling), so that longitudinal analysis and multiple sampling cannot be carried out, which disables the evaluation of time histories. In addition, the effect of dehydration is also a major concern when one is working with samples of low mineral concentration by the above-mentioned techniques. With prior dehydration, mineral loss and the actual depth of carious dentin are underestimated, due to the shrinkage of the specimen (ten Cate et al., 1991; van Strijp et al., 1995).

The x-ray attenuation method has long been appreciated as a sensitive measurement of atomic composition and density, and has been widely used in the determination of mineralization (Kinney and Nichols, 1992). Attenuation mechanisms relevant to CµCT x-ray passage through materials are the photoelectric and the Compton effects. At high energy levels, attenuation is dominated by Compton scattering, whereas at low energies the photoelectric effect is an important contributor. With photoelectric absorption, the incident x-ray photon energy is completely transferred to a core electron of the absorbing atom. The electronic excitation energy is emitted by secondary processes (i.e., auger electrons, fluorescence photons), which mostly do not contribute to the detected image signal. The Compton effect is the scattering of the incident photon at one atomic electron, resulting in a scattered photon with lower energy and the electron accepting the remaining energy. The scattered photon can be further scattered by small angles and therefore detected at erroneous positions in the detector. This leads to a scattering background in the projection (Bonse and Busch, 1996). As previously noted (Ritman, 2004), if the x-ray photon-energy is less than 25 keV, the x-ray interaction with matter is predominantly by the photoelectric effect, whereas in scanners where the photon energy generally exceeds 50 keV, it is predominantly by Compton scattering.

Microradiography (MR) is one x-ray absorption technology that has been commonly used for determining mineral content (ten Cate, 2001; Boivin and Meunier, 2002). An important limitation of this method is that, regardless of the resolution in the plane of section (around 10 µm), measurements of mineral content are integrated over the section thickness (typically ~ 100 µm), so that any variation in this plane is averaged out (Dowker et al., 2003). Also, the thinnest sections that allow sample integrity to be maintained (50-100 µm) are too thick to prevent image blurring from overlapping microstructural features in the tissue (Kinney and Nichols, 1992), and, in addition, shrinkage can occur during preparation, which may lead to underestimation of quantitative parameters such as mineral loss and lesion depth (ten Cate et al., 1991).

Under these circumstances, a non-destructive technique facilitating the three-dimensional determination of tissue-level mineral density profiles is highly desirable. µCT, as a form of x-ray microscopy, provides volumetric x-ray attenuation measurements for the completely non-destructive evaluation of materials, revealing the spatial distribution of attenuation coefficients (µ) within the object (Davis and Wong, 1996). There are two types of µCT available: synchrotron radiation microcomputed tomography (SRµCT) systems that can produce parallel monochromatic x-ray beams (Lewis, 1997), and commercial or in-house-developed desktop systems that can produce polychromatic x-rays with cone-beam geometry (Wong et al., 2000). Ideally, mineral density measurements should be conducted on SRµCT systems, where the power of a synchrotron source allows for the selection of a very intense monochromatic beam to facilitate the accurate quantitation of Linear Attenuation Coefficients (µ), thereby avoiding density calibration and beam-hardening corrections required for polychromatic laboratory x-ray sources (Dowker et al., 2004). However, since synchrotron radiation is emitted by high-speed electrons spiraling in a magnetic field of a particle accelerator (Lewis, 1997), there is limited access (Elliott et al., 1998). If polychromatic radiation is used, the x-ray spectrum shifts toward higher energy (beam hardening) as the attenuation through the specimen increases, because low-energy photons are generally more attenuated than high-energy photons. The resultant beam-hardening artifacts lead to increasing underestimation of µ toward the center of the specimen, but these artifacts can be minimized (not eliminated) by careful correction. The physical limitations of conventional polychromatic µCT (CµCT), such as cone-shaped beam geometry, beam divergence, and limited intensity flux, exert a major impact on the accuracy of a quantitative determination of mineral density (Chappard et al., 2006). Nevertheless, CµCT has been applied to quantitative studies of mineralized tissue, including bone, enamel, and dentin (Mulder et al., 2004; Wong et al., 2004; Willmott et al., 2007).

Beam hardening is arguably the most problematic issue for accurate MD determination. Recently, several protocols have been established for CµCT to assess beam-hardening artifacts associated with CµCT imaging and to ensure that accurate MD measurements can be obtained. The primary purpose of this review is to evaluate several important aspects of beam hardening associated with quantitative CµCT, which are most likely to render inaccuracies in the assessment of calcified tissue mineralization. Specifically, the following areas are critically characterized: (1) beam filtration during the scan, (2) beam-hardening correction during reconstruction, and (3) mineral density calibration.

(1) Beam Filtration during Scanning

The basis of computed tomography is the measurement of the attenuation of x-rays (photons) passing through an object. It is important to note that x-ray energy from a desktop micro-CT is polychromatic—that is, there is a continuous spectrum of x-ray energies emitted for any given potential setting. A spectrum of energies has an important practical consequence referred to as beam hardening. The x-ray spectrum, usually described in terms of the effective x-ray energy (keV), is arguably the most important variable to control to minimize beam-hardening artifacts. The total “effective” spectrum is determined by several factors, including: energy input of the x-ray source; autofiltration, both by absorption of photons generated beneath the surface of an x-ray source anode target and by passage through the tube exit port; other beam filtration introduced for the selective removal of low-energy x-rays; and the relative efficiency of the detectors to different photon energies (Tucker et al., 1991). Image contrast arises from variations of Linear Attenuation Coefficient (µ) within the sample material. This distribution map of µ values can be interpreted as a coarse approximation of the density distribution of the given sample and therefore allows different materials to be distinguished by µCT. A desirable feature of the low photon energy is the higher x-ray attenuation, thereby allowing for better discrimination of tissue types, especially soft tissues. While maximum contrast can be achieved when low energies are used, the photon energy has to be high enough to ensure that a sufficiently large number of x-rays penetrate the sample in an acceptable time. If the energy is too high, only a few photons are absorbed, and therefore the sensitivity for small changes in µ decreases.

Although x-ray attenuation can be related to the density of the material being scanned (Elliott et al., 1998; Nuzzo et al., 2002a,b), beam hardening compromises this conversion. Beam hardening also results in artifacts that appear as cupping, streaks, dark bands, or flare artifacts (Duerinckx and Macovski, 1978; Joseph and Spital, 1978; Barrett and Keat, 2004). Fortunately, in most applications the principal image errors that result from the use of polychromatic x-ray spectra can usually be minimized by arranging the experiment in a suitable way.

The only way to eliminate beam hardening completely is with monochromatic x-rays. Filtering can be performed to obtain a monochromatic beam by using Bragg reflection to pass x-rays of only a single energy (Bonse and Busch, 1996). However, the intensity of the beam produced by an x-ray tube after filtering is reduced by several orders of magnitude, thereby compromising the sufficiency of x-rays to penetrate the sample in acceptable time, and as a result, data acquisition is rather impractical for CµCT. With the advent of synchrotron radiation (SR), where x-rays are produced in highly specialized national laboratories, the intensities of the x-rays are much higher, and monochromatization of the polychromatic beam can be achieved while extremely high intensity is still maintained. The filtering by Bragg reflection can be adjusted to produce monochromatic x-rays of different energies, so the source can be tuned for specific materials and object sizes.

Some promising approaches to the conversion of a polychromatic spectrum into monochromatic or quasi-monochromatic spectra for desktop microCT are also in development. The one discussed below involves specific x-ray source anode materials and matched band-pass filter materials. As noted earlier, x-ray source anode materials can be selected for their characteristic Kα emission radiation (e.g., 8.0 keV for Cu, 17.5 keV for Mo, and 22.1 keV for Ag). This radiation output can then be filtered through a thin metal foil selected to have a K absorption edge at an energy just above the Kα of the respective anode material (e.g., 8.3 keV for Ni, 18.0 keV for Zr, and 24.4 keV for Pa), which predominantly attenuates the x-ray photons with energies above and below the Kα characteristic radiation energy (Lopes et al., 2000; Ritman, 2004). For example, the use of a powerful laser to elicit characteristic Kα emission (e.g., 17.5 keV for Mo) from a suitable target material, so that when combined with a suitable foil filter, little bremsstrahlung contamination occurs, and a resultant < 400 eV bandwidth at full width at half maximum (FWHM) of the spectrum of the Kα peak is possible (Lopes et al., 2000). However, as discussed, insufficient numbers of x-rays at the detector resulting from filtration necessitate increased exposure time by several orders of magnitude.

The following method was shown to compensate for the scanning time while maintaining a relatively effective monochromatization (Wong et al., 2004). Effective monochromatization was achieved by setting the multichannel analyzer to count photons at an energy level that was inside either a 4% (narrow) or a 40% (wide) window centered on the Ka peak (22.1 keV) of Ag (the target of the microfocus generator). The number of x-ray photons in the 40% window was about 2.5-fold the count of the 4% window. At each data point, 5000 photons were counted in the narrow window. The data set from the narrow window was used to calibrate the data in the wide window by fitting a seventh-order polynomial to avoid artifacts associated with polychromatic radiation, and to improve the signal-to-noise ratio in the final reconstruction. The calibrated wide-window data were used for reconstruction. Nevertheless, data were not detailed with regard to bandwidth at full width at half maximum of the spectrum of the Kα peak. Given a rotation step of 1.434°, creating 251 projections over 360°, it still took an average time of 12 hrs to complete each scan, despite the time-saving strategy used.

The commercialization of this technology includes a range of suppliers:

• Scanco Medical (http://www.scanco.ch)

• Skyscan (http://www.skyscan.be)

• GE Healthcare (http://www.gehealthcare.com/usen/funimg/pcimaging/)

• Xradia (http://www.xradia.com)

• BIR ACTIS Volume CT (http://www.bio-imaging.com/indcompare.asp?c=1)

• Philips HOMX 161 (http://www.tsgxray.com/homx-161_tsg.htm)

• ImTek: MicroCAT II

Unlike home-made custom µCT, where it is possible to manipulate parts and detectors, commercial µCT systems are equipped with fixed x-ray sources, filters, and detectors. In a typical µCT, the energy of the x-ray source and current can be adjusted and optimized when different materials are scanned. The x-ray tube voltages can be adjusted typically in the range of 20-100 kVp, and currents below 200 µA, depending on the manufacturer.

Despite the availability of software and of other possibilities to correct for beam-hardening artifacts that result from the use of polychromatic x-ray spectra, it remains desirable to avoid beam-hardening artifacts altogether. Using the lowest possible energy to achieve partial attenuation, combined with an appropriate filter, provides the closest approximation to a narrow and single-peak spectrum.

Filtration is typically used to pre-harden the x-ray spectrum by removing low-energy x-rays. Meganck et al. introduced x-ray filters in conjunction with beam flattening as a method to reduce beam-hardening-induced cupping artifacts in bone-like materials on a commercially available µCT system (eXplore Locus SP, GE Healthcare Pre-Clinical Imaging, London, ON, Canada) (Meganck et al., 2009). Five choices are available for beam filtration: none, 0.254 mm aluminum (Al), 0.508 mm Al, 1.016 mm Al, and 0.254 mm Al followed by 0.254 mm copper (Cu). Each of these filters resulted in different x-ray spectra, so the effectiveness of each filter in reducing cupping was investigated in detail. Differences between the filters that used 0.254 mm Al and 0.254 mm Cu and the filter that used 1.016 mm Al were found. The filter that used 0.254 mm Al and 0.254 mm Cu reduced cupping to an undetectable level. As a practical issue, using the filter composed of 0.254 mm Al and 0.254 mm Cu required a substantial increase in the integration time to obtain adequate photon statistics at the detector, resulting in scans that were approximately 3.5 to 3.75 times longer in comparison with those achieved with no filtration. Analysis of previous data has shown that the spectrum transmitted by a 0.1-mm-Cu filter is very close to the spectrum transmitted by a 3.7-mm-Al filter (Jennings, 1988). The results of this study indicate a marked reduction in contrast and increase in noise with filtration, which can be explained by the fact that the number of photons at the lower energy levels decreases as filtration increases, resulting in an upward shift in the mean energy of the spectrum. As stated, increased energy compromises contrast, thus blurring discrimination of tissue types. Energy spectrum is fundamentally important to MD determination, since it is closely related to beam-hardening-induced artifacts; the most favorable pattern is a narrow and single-peak spectrum. However, multi-peak spectra could be identified by this study, which used a source voltage of 80 kV. Apart from the primary peak, a further pair of peaks occurred at 50 and 60 keV, which, we assume, are resulting from the interaction of tungsten-characteristic emission (stimulated only at voltages of 80-100 kV) and the energy dependence of GADOX scintillator detection efficiency of the x-ray detector (Ryder et al., 2002). This would also increase the likelihood for Compton scattering that may occur for some of the higher photon energies in this x-ray beam; accordingly, lower voltage than used for this study is indicated to generate a spectrum that is primarily in the energy range of photoelectric absorption after filtration (< 25 keV).

The overall goal of filtration is to use the lowest possible energy to secure partial attenuation combined with an appropriate filter to provide a narrow and single-peak spectrum. A summary of effective energy levels, derived from different µCT systems using different voltage settings, is presented in the Table. However, it should be noted that to have one single energy number as the ‘effective’ energy does not fully describe all the properties of the spectral composition of the beam; the instability and aging of the source further alter the estimation of an accurate effective energy level (Nuzzo et al., 2002b). Since attenuation coefficients are very dependent on x-ray energy, the altered energies of a polychromatic beam lead to different attenuations of the same material (Elliott et al., 1998).

Table.

Reported Effective Energy Levels in Various Studies

Effective Energy Level (keV)	Studies
22.1	Anderson et al., 1996; Wong et al., 2004
40	Dowker et al., 2003; Willmott et al., 2007
26.6	Schweizer et al., 2007
24	Mulder et al., 2004
31	Mulder et al., 2004
60	Huang et al., 2007

(2) Beam Hardening Correction during Reconstruction

To compensate for beam-hardening effects on reconstructed linear attenuation values, other studies utilized linearization procedures based on step-wedge calibration or polynomial-based approaches to correct beam-hardening artifacts (Mulder et al., 2004; Burghardt et al., 2008).

A wedge-shaped phantom composed of a 200-mg HA/cm³ HA-resin mixture was first introduced to generate a voltage-specific beam-hardening correction (Burghardt et al., 2008). This concentration was assumed to be a reasonable approximation of apparent mineral density (averaged over the bulk sample volume) for cancellous bone biopsies/necropsies and whole-bone samples from small animals (Kazakia et al., 2008). The phantom geometry is shown in schematic form in Fig. 1. The transmitted x-ray intensity at each width of the wedge (I_meas) and the unimpeded reference intensity (I₀) were measured along the length of the wedge. The deviation of the absorption curve from linearity indicates the degree of beam hardening (Fig. 2).

Figure 1.

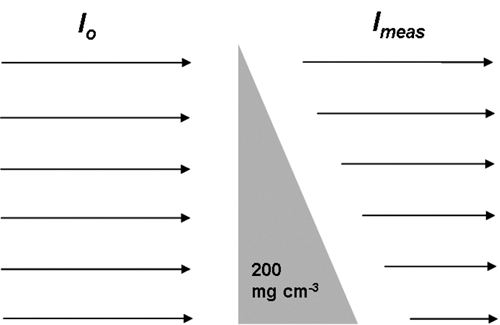
Schematic diagram of the wedge for beam-hardening correction.

Figure 2.

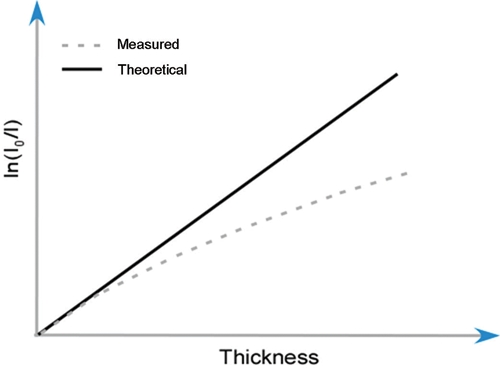
Schematic diagram of the deviation of the measured ln(I₀/I_measured) from ln(I₀/I_theoretical).

It is possible to define a voltage-specific polynomial correction term as an optimal correction function (ε_v), derived from the difference between ln(I₀/I_theory) and ln(I₀/I_meas). Corrected absorption values ln(I₀/I_corr) are calculated for tomographic acquisitions based on the following expression, derived from the Lambert-Beer law:

$$\ln \left(\frac{I_0}{I_{corr}}\right)=\ln \left(\frac{I_0}{I_{meas}}\right)+{\epsilon }_v\left[\ln \left(\frac{I_0}{I_{meas}}\right)\right]$$ (1)

$${\epsilon }_v=A_0+A_1\times \ln (I_0/I_{meas})+A_2{[\ln (I_0/I_{meas})]}^2+A_3{[\ln (I_0/I_{meas})]}^3$$ (2)

Eq. (2) represents a polynomial expansion form of eq. (1) in third-order, where A₀-A₃ are the polynomial correction values—for instance, A₀ corresponds to the 0-order coefficient, A₁ to first-order, and so on.

In a commercially available reconstruction software package (NRecon, SkyScan, Aartseelar, Belgium), beam-hardening correction utilizes a second-order relationship: ε_v = A₂[In(I₀/ I_meas)]². The options in the program allow the operator to select the A₂ level from 0% to 100%. It is claimed that this type of correction is suitable for most objects, covering the density range from 0 to 3-4 g cm^-3 (from air to bones, plastics, light metals, etc.). Two reconstructed virtual slices through a phantom composed of pure HA with A₂ set as 0 and 1 are shown in Fig. 3. Distinct beam-hardening effects were present without beam-hardening correction, whereas those were almost entirely absent with the second-order correction algorithm being implemented, which could also be reflected by the stable 1-x-ray intensity profile across the reconstructed image (Fig. 3).

Figure 3.

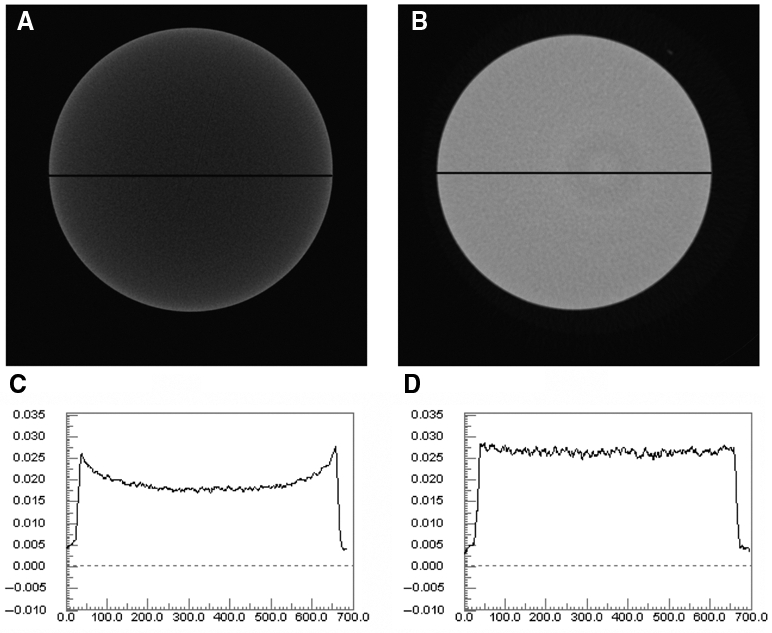
Influence of the beam-hardening correction. (A) Cross-section through a 12-mm sample, scanned with radiation energy (100 kV, 100 µA), without implementation of the beam-hardening correction algorithm. (B) Same as (A), but with implementation of the second-order correction algorithm. (C) Line profiles through the cross-sections of (A). (D) Line profiles through the cross-sections of (B).

The effect of beam-hardening may be further reduced by the application of a higher-order correction function to the detected x-ray radiation attenuation for more dense objects or complicated compositions. In a recent study, a voltage-specific correction equation used a third-order polynomial, with coefficients 0, -0.44, 0.78, and -0.09 assigned to A₀-A₃, respectively, in eq. (2) (Burghardt et al., 2008). It was noted that the results are CT-scanner- and calibration-standard-dependent, since conversion relations could be quite different for CT scanners having different effective x-ray beam energies and different beam-hardening and scatter properties and corrections.

However, evidence of beam-hardening artifacts was found despite the use of a beam-hardening correction algorithm based on a 200-mg HA/cm³ wedge phantom (Kazakia et al., 2008). It was suggested that the density of the wedge phantoms used to produce the correction factor should be chosen based on maximum tissue density (1200 mg HA/cm³) rather than mean apparent density of the specimen (200 mg HA/cm³), as has been a common approach in the past.

A symmetrical seven-step Al wedge with steps of known thickness and mass per unit area has also been used for beam-hardening correction (Davis and Elliott, 2003). For each CCD column, a fifth-order polynomial was fitted to the measured attenuation against the calculated attenuation for a nominal monochromatic beam and used to correct for the recorded projections. Although this method works ideally only when the attenuation vs. energy characteristics of the specimen match those of Al, it reduces the beam-hardening artifacts considerably and provides a good approximation of equivalent monochromatic x-ray attenuation for biological specimens (Willmott et al., 2007).

Beam-hardening effects also lead to a non-linear relationship between mineral density and a linear attenuation coefficient of radiation measured by µCT (Nazarian et al., 2008). The attenuation becomes more underestimated with increasing density. It has been reported that by the implementation of the beam-hardening correction algorithm, the non-linear relationship was eliminated (Mulder et al., 2004), and measurements became almost independent of the orientation of the sample (Postnov et al., 2003).

The reliability of µCT measurement of peri-implant bone, especially at the interface between a titanium implant and bone, is greatly anticipated in implant research for enhancing and quantifying osseointegration of dental implants. However, it has been shown that beam hardening very strongly affects the reconstruction quality of current µCT machines. The emergence of prominent dark-streak artifacts in the areas of sharp density transitions makes the reconstructed regions close to the surfaces of titanium implants unreliable, rendering erroneous the interpretation of osseointegration (Butz et al., 2006). Depending on the implant thickness and the radiation parameters, the artifact-affected region extends to various distances from the bone-implant interface: 200 µm (Bernhardt et al., 2004), 45 µm (Rebaudi et al., 2004), 60 µm (Stoppie et al., 2005), 24 µm (Butz et al., 2006), and 350-400 µm (Park et al., 2009).

It should also be recognized that the choice of the reconstruction method itself can correct several kinds of artifacts (Wang et al., 1993; Grass et al., 2000). To address inherent metallic halation artifacts, simple backprojection algorithms such as the Feldkamp algorithm might be inadequate (Feldkamp et al., 1984), since the projection data used as the basis for the reconstruction process do not correspond to the simplified model underlying the backprojection-based 3D reconstruction. It is well-known that algebraic reconstruction (ART) can deal more effectively with missing or corrupted data (De Man et al., 1999, 2000, 2001; Zhang et al., 2007), since ART is very flexible and mathematical constraints can be quite simply integrated into the reconstruction process. In a general sense, ART describes iterative techniques that find a best-fit solution from solving a huge set of projection equations. ART would allow for a more sophisticated modeling of the actual physical properties of the image acquisition process (Schulze et al., 2010). However, ART requires several iterations and considerable computational power, making it impractical for such reconstruction to be adapted to µCT systems. In commercialized desktop µCT systems, to our best knowledge, the reconstruction algorithm in use is still the simple Feldkamp algorithm or modified Feldkamp algorithm, due to its computational efficiency.

(3) Density Calibration

Rather than reporting µ values, transforming these into mineral density g_HAp cm^-3 [the mass of hydroxyapatite (HA) per unit volume] is always preferable. The advantage of this conversion is that the significance of the measurement is more easily appreciated, and recordings are more easily compared with other work. Therefore, calibrating a µCT system for mineral density values becomes a major challenge within the mapping process of mineral density gradients. Different solutions have been studied with various calibration standards and underlying assumptions, to estimate the attenuation for the observed tissue.

If a series of phantoms with different concentrations of minerals is simulated, a linear relationship between grey level (µ) and mineral density can be generated from these phantoms, allowing the measured grey value of a sample to be converted to an estimated mineral density (Huang et al., 2007; Zou et al., 2009). This is straightforward and does not depend on the spectral composition of the x-rays, which may be a source of error in CµCT studies. However, the calibration standards need to fulfill several basic requirements to be useful for the calibration of modern µCT scanners: (a) Their x-ray attenuation must reflect the absorbance of the interested object and should cover a representative range of mineral densities, and (b) they must be homogeneous at the spatial resolution of the scanner (Schweizer et al., 2007).

Hydroxyapatite (HA) is the major component of bones and teeth. It has been widely used as a bone substitute in clinical studies and as the experimental phantoms in calibration standards. When it comes to practical application, the form of the composite containing hydroxyapatite crystals varies, necessitating the selection of different matrix materials; however, the method of establishing a calibration curve remains. The application of this approach is described in the following section.

Owing to solubility limitations, it is impossible to obtain a homogeneous solution of HA for calibration purposes. An alternative for HA, dipotassium hydrogen phosphate (K₂HPO₄), was introduced by Witt and Cameron in the 1970s (Witt and Cameron, 1970). K₂HPO₄ liquid calibration phantoms are similar in atomic weight and x-ray absorption characteristics to HA over a wide range of energies (Nuzzo et al., 2002b; Schweizer et al., 2007; Nazarian et al., 2008), but are soluble in water and therefore far more homogeneous at the microscopic level.

Aluminum (Al) is a convenient material that has an atomic number close to the effective atomic number of HA (Elliott et al., 1998; Nazarian et al., 2008), with atomic numbers of 13 and 15.86, respectively, for Al and HA (Dowker et al., 2004). Therefore, a pure aluminum (Al) wire was placed longitudinally next to the object and exposed simultaneously as a reference material that was visible in every single slice (Wong et al., 1995, 2000, 2004; Clementino-Luedemann et al., 2006; Clementino-Luedemann and Kunzelmann, 2006; Willmott et al., 2007). The µ values were standardized by using the measured mean µ of the pure aluminum wire and its theoretical value at the effective energy level from a published database (NIST, Gaithersburg, MD, USA). Based on the assumption that the mineral was HA, with a density of 3.15 g cm^-3, the µ values were converted to mineral concentrations of enamel by:

$$C_e=\frac{{\mu }_e·{\mu }_{Al(pub)}}{{\mu }_{Al}·{\mu }_{mHA}}$$ (3)

where µ_e is the measured µ of enamel, µ_Al(pub) the µ of aluminum wire from published data, µ_Al the measured µ of aluminum wire, and µ_mHA the mass attenuation coefficient of HA from published data.

The popularity of aluminum standards can be traced to its successful application for the determination of mineral concentration from x-ray attenuation measurements by both quantitative MR and µCT equipped with monochromatic x-ray sources (Angmar et al., 1963; Elliott et al., 1981, 1998; de Josselin de Jong and ten Bosch, 1985). If one or more aluminum step-wedges, with steps of known mass per unit area, are placed next to the section, the attenuation of enamel of a given thickness is then reported as the equivalent thickness of aluminum, which gives the same optical density. As reported, the linear attenuation coefficients (µ) of calcified tissues are preferably expressed as the µ of Al at the applied photon energy, which neatly avoids the need to measure x-ray intensity_, a potential source of error in photon counters (Elliott et al., 1998).

Other compounds, such as potassium pyrophosphate (K₄P₂O₇), also have attenuation properties similar to those of HA, yet their application as bone calibration phantoms has not been as extensive as that of K₂HPO₄ (Sanada et al., 1999).

(3.1) Bone Research

Bone architecture and mineral density are regarded as key factors in determination of the biomechanical properties and fracture risks of trabecular bone (Smith and Smith, 1976; Rice et al., 1988; Rho et al., 1995; Bo et al., 2001). In the past few years, µCT has been used extensively as a principal standard to quantify the micro-architectural properties of bone; the possibilities for the application of µCT in the quantification of the degree of mineralization of bone have also received much attention (Nuzzo et al., 2002b; Postnov et al., 2003; Mulder et al., 2004; Schweizer et al., 2007; Burghardt et al., 2008; Kazakia et al., 2008; Nazarian et al., 2008).

Bone is composed of two phases: a highly attenuating calcium phosphate mineral component and a soft-tissue-equivalent organic phase (Burghardt et al., 2008). The underlying assumptions made to estimate the attenuation of the observed tissue are that the mineral phase of bone is calcium and phosphate, bound in the form of HA; x-ray absorption in the organic part remains constant (approximately 7%), regardless of changes in mineral content. The latter hypothesis was confirmed by a study in which completely demineralized bones were scanned by a CµCT system (Postnov et al., 2003; Mulder et al., 2004). For the characterization of trabecular bone, a spatial resolution of about 10 µm, much smaller than the typical size of trabecular bone structures (~100 µm), was shown to be a good compromise to obtain a large field of view, but with sufficient detail and reduced partial volume effects (Nuzzo et al., 2002b; Chappard et al., 2006).

In the following, three well-established processing techniques for mineral density calibration are presented to illustrate the various approaches outlined above.

HA-Resin Phantom

MD calibrating phantoms are provided by commercial µCT manufacturers. A good example is the phantom provided by Scanco Medical, consisting of 5 cylindrical inserts of different concentrations (0, 200, 400, 600, and 800 mg/cm³) of hydroxyapatite particles (≤ 30 µm in size) embedded in PMMA to mimic surrounding soft tissue (Cheng et al., 2000; Zheng et al., 2000; Nuzzo et al., 2002b; Chueh et al., 2006; Burghardt et al., 2008; Nazarian et al., 2008). The whole phantom has a diameter of 35 mm and is 30 mm high. The hydroxyapatite cylinders have a diameter of 6 mm and a height of 30 mm. In contrast, SkyScan has a slightly different calibrating system, where fine HA powder is uniformly embedded in epoxy resin, forming individual HA-resin rods of various diameters to match the calibrated bone samples (2, 4, 8 mm correspond to mouse, rat, and rabbit, respectively). Phantom MD values range from 50-750 mg HA/cm³. If a custom µCT is used, evaluations of the features—such as in-plane and axial spatial resolution, noise and uniformity, and artifacts incurred by reconstruction algorithms—can be aided by a series of phantoms at QRM GmbH (http://www.qrm.de/content/products.htm), in a direct, visible manner. A phantom housing 5 cylindrical inserts containing various densities of HA (0, 50, 200, 800, 1000 mg/cm³) is available for bone density calibration purposes.

As noted previously, the reference material must be homogeneous at the micrometer scale such that the standard deviation of the attenuation coefficient in a given area is reduced to a minimum (Schweizer et al., 2007). Unfortunately, some phantoms currently available appear inhomogeneous at the scale used for µCT imaging (~10 µm), and the non-uniform distribution of the powder, presumably occurring during resin mixing and curing, results in the granular nature of the images, contributing to larger variations in linear attenuation (Bonse et al., 1994; Nazarian et al., 2008). Additionally, a limitation and potential source of error in the calibration scheme are the range of HA concentrations represented in the phantoms (0-800 mg/cm³) (Burghardt et al., 2008). Because the biological upper range of mineral density typically exceeds 1000 mg/cm³, extrapolation of the calibration curve is necessary for most applications in bone and tooth biology. Beyond these concentrations, it is difficult to manufacture relatively homogeneous HA-epoxy resin mixtures. Also, the calibration relationships have been shown to be different for standards made by the various manufacturers (Goodsitt, 1992). This presumably is due to differences in composition of the resin, filler, and HA components.

Another general principle is that the x-ray attenuation of the calibration phantoms during scanning must match approximately the attenuation of the sample and any surrounding tissue or water. Meganck and co-workers reported an enhanced sensitivity of calibration by using an acrylic tube of distilled water (beam flattener) to ensure equivalent path lengths of the x-ray beam, as if the phantom and specimens were imaged individually. To achieve this, they immersed the specimens in an identical water tube for every scan (Meganck et al., 2009). Although beam flattening has the effect of normalizing the beam path length within the field of view for each sample scan, most studies failed to take it into consideration, partly attributed to the fact that most phantoms provided by manufacturers do not have a comparable diameter to approximately match the cross-sectional thickness of the calcified tissue scanned. For instance, solid-state phantoms of HA rods (see http://www.qrm.de) having a diameter of 32 mm, the average diameter of a fat mouse or a lean rat, were used for the study of typical mouse or rat bone features (distal femur, proximal tibia, lumbar vertebra) only 2 mm and 4 mm in diameter. From this point of view, SkyScan provides phantoms with diameters better matched to the bone samples. This also implies that separate scans must be used for individual samples, because the simultaneous scanning of multiple samples renders a significant underestimation of MD, in addition to suboptimal image signal-to-noise ratio and spatial resolution.

No absolute standards exist for CµCT measurements, making it difficult to conduct any direct comparison between values obtained with different calibration systems. SRµCT is considered an appropriate standard reference technique. By comparing CµCT mineralization evaluation of a bone sample with that measured by SRµCT, it was found that MD was significantly underestimated, with MD values 15.0% lower than SRµCT values (Kazakia et al., 2008). The HA-resin phantom (0-800 mg/cm³) may be one important source of error, since the majority of voxels within adult human bone specimens are at a mineralization level greater than 800 mg HA/cm³. Therefore, extrapolation of the calibration curve is necessary to convert attenuation to HA concentration. Since beam-hardening artifacts will also exist in the phantom scan and are clearly dependent on density, it is possible that extrapolation causes errors in the calculation of high-intensity voxels (Schweizer et al., 2007).

Another way to verify these MD measurements is to compare them with physical measurements that are typically performed by ashing (Magne, 2007; Kazakia et al., 2008). Even though there is a high correlation between the µCT-based densitometry measurements and ash weights, which is an average value for a large number of bone voxels containing both cortical and trabecular bone, making MD estimates on a voxel-by-voxel level should still be avoided because this type of measurement would be prone to image quality issues such as noise and partial volume artifacts (Wong et al., 2004). However, it is possible to visualize clearly the distribution patterns of mineralization based on grey-scale values.

HA-Li₂B₄O₇ Solid Phantom

To fulfill the requirement that the calibration material should cover a representative range of mineral densities, a recent development has opened a new avenue for the calibration of local bone mineral densities.

Fusion of pure HA with Li₂B₄O₇ with the capacity to achieve mineral density concentrations ranging between 120 and 740 mg/cm³, in conjunction with pressed and sintered pellets of pure HA, extends the phantom calibration range densities up to 3050 mg/cm³ (Schweizer et al., 2007). HA-Li₂B₄O₇ phantoms can be prepared by the dissolution of HA in a flux of Li₂B₄O₇, a traditionally used glassy solid solvent with a low x-ray absorption coefficient, at a temperature of 1300°C for 10 min, with an oxygen/natural gas flame under constant agitation in a commercial fusion machine (Autofluxer, Breitländer, Germany). One can adjust the mineral concentrations very easily and precisely by mixing known weights of the flux and the mineral before fusion. The second set of standards used by these authors was prepared by compaction of HA directly in a hydraulic press at different pressures, ranging from 1 to 5 tons, prior to sintering.

However, there are many open questions before the material can be applied as an actual calibration standard. Recent studies in our laboratory (Zou et al., 2009) have indicated that composite phantoms may overcome the need for extrapolated calibration; however, differences in background matrix between these phantoms must be taken into account. It is also not clear how calibration performed as a separate acquisition apart from the specimen, as done by Schweizer et al. (2007), differs from a single acquisition incorporating internal calibration standards (Burghardt et al., 2008). Additionally, the combined calibration curve was obtained after subtraction of the absorption caused by the mass fraction of Li₂B₄O₇ matrix; therefore, the contributions of organic phase and water were ignored.

K₂HPO₄ Liquid Phantom

At the University of California San Francisco (UCSF), the calibration standards containing liquid solutions of dipotassium hydrogen phosphate (K₂HPO₄) have been in use since the late 1970s (Faulkner et al., 1993). Similar calibration standards are now in worldwide use. They were scanned simultaneously by quantitative computed tomography (QCT). With this kind of calibration system, bone mineral results are expressed as an equivalent density in milligrams of K₂HPO₄ per milliliter of bone tissue.

Liquid K₂HPO₄ solutions have also been used in µCT studies. A study by Nazarian et al. (2008) presented observations showing that both HA-SCANCO solid and K₂HPO₄ liquid calibration phantoms can be used to assess bone mineral density. K₂HPO₄ solution represents a two-phase mixture, with K₂HPO₄ representing the mineral phase, and water representing the non-mineral elements (Nuzzo et al., 2002b). The advantage of the K₂HPO₄ liquid calibration phantom is not only that it reduces non-homogeneities within liquid phantoms, but it also has the ability to be placed in a variety of media, mimicking different tissue properties (soft tissue, fat) or using different specimen preservation techniques (fresh frozen, saline, formaldehyde, ethyl alcohol, air). This is not possible with the HA-SCANCO calibration phantoms, since the calibration phantom rods are embedded in resin (Nazarian et al., 2008).

Researchers have experienced some problems with these liquid standards. The chief complaint is air bubble formation. Air bubbles arise from: (1) the equilibration of the liquid solutions with air dissolved in the plastic material (a phenomenon known as ‘out-gassing’), and (2) the evaporation of water through imperfect seals. Out-gassing does not change the concentration of the solution and is therefore of minor importance. The bubbles form at a rate of about 500 µL/yr, and can be removed from the solutions in phantoms that incorporate bubble traps. The evaporation of water is definitely a problem with many homemade and commercial phantoms. It results in more concentrated solutions (Goodsitt, 1992; Schweizer et al., 2007), which may be solved by regular replenishment or replacement, e.g., 3 mos, during which the liquid phantom was shown to be leak- and bubble-free (Nazarian et al., 2008). If properly performed with carefully prepared solutions, the refilling of these liquid phantoms will not adversely affect the calibration values.

Overall, up to the limit of solubility (1000 mg/cm³), the K₂HPO₄ liquid calibration phantoms provide a cost-effective, easy-to-prepare, and convenient means to perform quantitative µCT analysis (Nazarian et al., 2008).

(3.2) Dental Research

In an attempt to understand the physicochemical processes of caries attack, investigators have undertaken extensive quantitative studies of mineral distributions in natural and artificial caries lesions using microradiography (MR) (ten Bosch and Angmar-Månsson, 1991; ten Cate et al., 1991; Kinney and Nichols, 1992; Dowker et al., 2004; Wong et al., 2004). MR provides a high-resolution but destructive and two-dimensional assessment of a three-dimensional calcified tissue structure. However, a so-called ‘single-section model’ made the destruction of a sample unnecessary (Klont and ten Cate, 1991; Mukai et al., 2001; Mukai and ten Cate, 2002), and determination of the mineral content profiles of the lesions, lesion depth between incubations in vitro or between exposures to the oral environment, can be conducted repeatedly on MR. In this unique model, thin sections were prepared and embedded in the dentin-bonding agent, and sandwiched between two glass plates, with only the experimental surfaces being cut open (Kinney et al., 1994; Kawasaki et al., 1999; Mukai et al., 2001; ten Cate, 2001; Mukai and ten Cate, 2002). Nevertheless, longitudinal studies of lesion formation are still restricted to essentially 2D model systems, in which the lesion develops within the plane of the thin section, providing limited representation of a lesion formed in a whole tooth (Dowker et al., 2004). In addition, the authors did not consider that a sealing agent can affect the organization of the investigated structure and thus the mechanisms of demineralization or remineralization.

Alternatively, µCT provides non-destructive, three-dimensional images of an object, making it possible to generate localized 3D imaging of the development of lesions within an uncut tooth that can be assessed after each series of demineralization or remineralization episodes.

µCT with a synchrotron x-ray beam has been used to study natural caries lesions from dentin (Kinney et al., 1994) and enamel (Kinney and Nichols, 1992). However, longitudinal studies with repeated measurement of specimens over a series of demineralization or remineralization episodes are not practical, owing to the limited availability and cost of SRµCT (Dowker et al., 2003).

In the last few years, CµCT has been utilized for the study of the dynamic processes of demineralization and remineralization in dental caries, including enamel (Wong et al., 2000, 2004; Dowker et al., 2004; Clementino-Luedemann and Kunzelmann, 2006; Huang et al., 2007) and dentin (Kinney et al., 1994; Clementino-Luedemann et al., 2006; Clementino-Luedemann and Kunzelmann, 2006; Willmott et al., 2007). While the use of K₂HPO₄ liquid calibration phantoms and HA-resin solid phantom has become commonplace in bone research, calibration schemes used in dental research for CµCT have focused on aluminum. Other reference materials have not been extensively studied for research-based CµCT imaging.

(3.2.1) Enamel

Enamel is a highly mineralized crystalline structure. It contains, on average, 95% inorganic substance, 4% water, and 1% organic substance by weight. The inorganic substances have been reported to vary from the outer enamel surface to the enamel-dentin junction (EDJ); the mineral content and the density were reported to decrease toward the EDJ (Weatherell et al., 1974). The mineral content of outer enamel falls off from the cusps toward the cervical region (Weatherell et al., 1974). These features were also consistent with CµCT observations (Wong et al., 2004).

Aluminum Reference

There have been numerous experimental attempts to measure the MD of enamel by CµCT. The majority of these measurements have been performed with a pure Al wire placed alongside the tooth rod for calibration. This method is advantageous because one can standardize the mean µ for each image using the ratio of the published theoretical µ for Al to the measured value and assuming that HA is the only content in enamel (see eq. 3). In contrast, it is also necessary to point out that Al facilitates calibration only when the attenuation vs. energy characteristics of the specimen match those of Al. Although the ratio of attenuation coefficient of sound enamel to that of aluminum was reported to be nearly independent of energy (Elliott et al., 1998), many uncertainties and variations in the composition of sound and carious enamel limit the accuracy of the determination of mineral concentration from the µ. In addition, an accurate evaluation of the effective energy level becomes particularly important in such applications. As shown in eq. 3, the validity of calibration depends on the ratio of the theoretical µ for Al at the effective energy level to the measured values. In contrast, the concept of effective energy level has become unnecessary by the construction of a linear curve between measured grey values (µ) and known mineral densities of calibration phantoms, where a direct assessment of effective energy level is avoided.

Pure HA Solid Phantoms

In a recent study, Huang et al. (2007) introduced pure HA phantoms to quantify mineral density (MD) of white-spot lesions (WSLs) for the first time, based on the assumption that the mineral phase of enamel is the only x-ray-absorbing component. With HA phantoms of various densities as internal standards, the MD of WSLs was quantified accordingly. In a solid form, pure HA was used to represent the mineral phase in bones and teeth (Postnov et al., 2003; Huang et al., 2007). While solid HA phantoms have been proven to be spatially homogeneous (He et al., 2007; Huang et al., 2007; Schweizer et al., 2007), and were capable of spanning the highest and lowest densities in carious and sound enamel (approximately 1200-3000 mg/cm³), a lack of phantoms with densities below 1400 mg/cm³ remains, due to manufacturing limitations (He et al., 2007). The advantages of this method are that: (a) HA is closest to the composition of natural enamel, (b) low-density HA phantoms have increased porosity very similar to that of demineralized enamel, (c) the phantoms provide internal standards to counteract any instrument fluctuation between samples, and (d) the measured grey values of sound and demineralized enamel fall mainly within the range of the grey values of the highest- and lowest-density phantoms, thereby producing an accurate calibration (Huang et al., 2007). However, errors have been introduced into the quantitative three-dimensional measurements of mineral concentration by the single-model assumption.

The variation and uncertainty in the composition of sound and carious enamel limit the accuracy with which enamel mineral concentrations can be determined from µ values. It is difficult, however, to simulate a standard exactly imitating the structure and composition of enamel. Fortunately, Dowker and co-workers (Dowker et al., 2004) have developed a numerical method to determine mineral concentrations on the basis of model compositions. Close SRµCT inspection of mineral concentration in enamel explored the effects of composition and density by modeling enamel as a two-phase system: an inorganic (HA) and an organic component (a, absent; b, water; c, polyglutamate). The results showed a negligible difference between models in which the organic phase was modeled as water or polyglutamate [(C₅H₇NO₃)_n, an approximation to protein].

(3.2.2) Dentin

Dentin constitutes the bulk of a tooth. On a weight basis, it consists of 70% inorganic minerals (mainly hydroxyapatite and some non-crystalline amorphous calcium phosphate), 20% organic material (90% of which is collagen and the remaining 10% ground substance), and 10% water (which is absorbed on the surfaces of the minerals, between the crystals, or within the tubules) (Linde et al., 1980; Marshall et al., 1997). Dentin is a complex hydrated composite consisting of three major structural features: (i) oriented tubules surrounded by (ii) a highly mineralized peritubular zone (1-2 µm in thickness) embedded in (iii) a less mineralized intertubular dentin (Zavgorodniy et al., 2008b). The closely packed tubules range in diameter from 0.9 µm near the DEJ or cementum to 2.5 µm adjacent to the pulp chamber. The organic component surrounds and exists within the tubules.

Dentin is generally susceptible to caries, an infectious and chronic dental disease process with a multi-factorial etiology. The carious process is not only associated with the loss of mineral matter, altered ultrastructure and chemical composition, and disintegration of the organic material, but also with various defensive reactions by the dentin-pulp complex to carious attack (Daculsi et al., 1987; Marshall et al., 2001). The most common observed defense reaction is the formation of caries-induced occluding of the tubules, described as a gradual mineralization of the tubule lumens, which can lead to complete obstruction of the tubules (Zavgorodniy et al., 2008b). In addition to the original biological HA mineral in sound dentin, Mg-substitute β-TCP (β-tricalcium phosphate) is also present in the resulting sclerotic dentin (Zavgorodniy et al., 2008a).

As a consequence of the porous nature of dentin, attributable to the tubular structure, the non-homogenously calcified peritubular and intertubular dentin, and the non-uniform inorganic phase, it is necessary to make some assumptions to estimate the mineral density of sound and carious dentin. Generally, the inorganic component in carious and sound dentin has been modelled, for simplicity, as pure HA, with a theoretical density of 3.156 g cm^-3 (Kinney et al., 1994; Anderson et al., 1996; Wong et al., 2000; Clementino-Luedemann et al., 2006; Clementino-Luedemann and Kunzelmann, 2006). The contribution of the organic phase was assumed to be constant (Willmott et al., 2007). Considering the current spatial detection limit of a CµCT (about 5 µm), it is not possible to investigate this structure at the tubular level, resulting in specimens being imaged at a relatively low magnification. As a consequence, the x-ray intensity of each pixel recorded corresponds to an averaged mineral density over a volume of the target specimen (~ 10 µm³). To reduce the influence of the recorded noise level, the intensity values are averaged by calculation of the mean grey levels of a small number of adjacent pixels, instead of the mapping of single pixel line profiles, generating a result that represents a more homogenous mixture of tubule, peritubular, and intertubular structure (Wong et al., 2000; Angker et al., 2004; Huang et al., 2007).

Using a synchrotron source, Kinney and co-workers (Kinney et al., 1994) mapped, for the first time, the three-dimensional mineral distribution of a carious human canine. They found that mineral concentrations for sound and demineralized dentin were 1.29 and 0.55 g cm⁻³, respectively. However, this work failed to take into account the contributions of water and organic material within dentin; the mineral phase was assumed to be the only absorbing part. This single-mineral-phase model continues to be the basis of interpretation, and few attempts have been made to reproduce this observation with CµCT systems (Anderson et al., 1996; Clementino-Luedemann et al., 2006; Clementino-Luedemann and Kunzelmann, 2006).

Recently, an x-ray microtomography study of the mineral concentration of carious dentin was carried out based on a two-phase assumption (Willmott et al., 2007). It was also noted that proteolysis of collagen was involved in the carious process; thus, errors may potentially arise from the assumption that the contribution made by collagen was constant. For this reason, the mineral concentrations were reported as a range rather than a specific value. Two extreme situations were simulated: The collagen concentration either remained unaltered (0.54 g cm^-3), or all the collagen was completely proteolytically degraded (0 g cm^-3).

Although µCT has been applied to the study of teeth since 1989 (Davis and Wong, 1996), little headway was made in terms of calibration standards in the ensuing 20 years. The scarcity of the currently available information on the mineral concentration of sound and carious dentin, from another aspect, reflects this issue’s complexity. While it has proceeded to two-phase models in studies of bones, the calibration method for dental research has lagged, since Al is still being used extensively for calibration of the mineral density of dentin (Anderson et al., 1996; Clementino-Luedemann et al., 2006; Clementino-Luedemann and Kunzelmann, 2006). As stated above, not only is the accuracy of this calibration method energy-dependent, but it is also dependent on the ratio of attenuation coefficient of dentin to that of aluminum, which may be altered by the variation of structure and composition, along with the dynamic carious process.

Since few attempts have been made to determine mineral density profiles accurately in carious dentin, due to the lack of suitable calibration standards, we sought to develop a two-phase calibration method and address the issue associated with the extrapolation of the calibration range obtained from either K₂HPO₄ liquid standards or HA-resin solid standards (Kazakia et al., 2008; Zou et al., 2009). Gelatin was considered an appropriate material of soft-tissue equivalence. However, the relative hydrophobicity of HAP precluded successful formation of a gel incorporating HAP with gelatin. Bearing in mind that K₂HPO₄ was substituted for HA when creating water-soluble systems, we incorporated gelatin with various quantities of K₂HPO₄ into discs, producing effective K₂HPO₄ densities ranging from 0 to 900 mg/cm³ (Schwass et al., 2009). Although easy to create, the resulting phantom discs were highly susceptible to variations in humidity. Dehydration and consequent shrinkage of the discs caused the effective K₂HPO₄ density to increase with time. It was readily apparent that discs involving a gelatin-K₂HPO₄ system would be inappropriate for practical experimentation, where it was expected each micro-CT scan could exceed 1.5 hours’ duration, where repeated calibrations are called for, and given that it would be desirable to use them for multiple scans.

Another observation—that a set of water-infiltrated porous solid HA phantoms (specimens were submerged in water, and vacuum-degassed for 1 hr to remove any air bubbles trapped in the pore spaces) was capable of expanding the calibration curve obtained from K₂HPO₄ solutions (Fig. 4)—is an interesting finding which could open additional possibilities for more accurate three-dimensional volume analysis (Zou et al., 2009). The significance of this work is that, for the first time, it has been possible to define a two-phase calibration standard for dentin. On this basis, the mineral densities covered ranges from the highest- and lowest-density values found in dentin, thus avoiding extrapolation of the calibration curve obtained from low-density K₂HPO₄ solution phantoms or high-density HA phantoms toward the actual mineral density values in dentin, and enabling a more rational mineral density calibration to be obtained.

Figure 4.

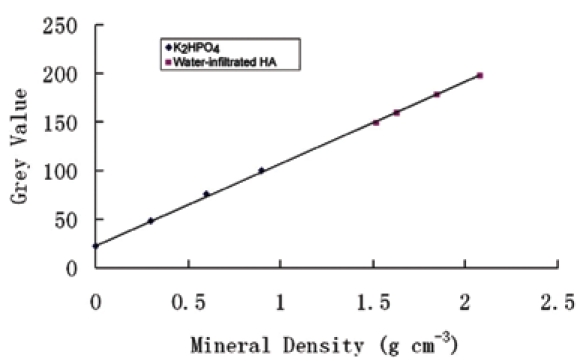
An expanded calibration curve from K₂HPO₄ solution phantoms and water-infiltrated HA phantoms.

As was documented recently (Schwass et al., 2009), a range of low-mineral-density phantoms was fabricated by the combination of TEGDMA/BIS-GMA resin with commercially pure HA powder densities from 70 mg/cm³ to 1050 mg/cm³. Sintered HA with various densities was also impregnated with the same resin, producing medium-density phantoms up to 1900 mg/cm³. Despite the manufacturer-stated presence of radiopaque components within the resin, the authors claimed that its influence was found to be practically negligible. Using these phantoms, the authors were able to establish linear grey-level calibration attenuation curves vs. MD or absolute density.

To date, µCT has been incorporated for study of the volume of carious dentin removed during cavity preparation in deciduous molars (Willmott et al., 2007); for assessment of a chemomechanical caries removal strategy (Hahn et al., 2004); for evaluation of a new enzyme solution for caries removal (Clementino-Luedemann et al., 2006); and for estimation of long-term remineralization of interproximal caries-like lesions adjacent to glass-ionomer restorations (Lee et al., 2008). Most quantitative evaluations have essentially used two-dimensional data extracted from a three-dimensional µCT data set. Ideally, mineral density measurement in three dimensions would most accurately represent caries lesions; however, tools to enable such measurements to be made are not readily available. In addition, natural caries lesions (in both enamel and dentin) are characterized by indistinct boundaries of different zones, due to the demineralization gradient (Zheng et al., 2003). Therefore, measurement of volumes associated with various degrees of demineralization would be of great relevance. Although reconstruction of a dentin caries lesion in three dimensions may be easily done (Wong et al., 2006), no value of mineral concentration for the boundary between sound and carious dentin is available in the literature (Wong et al., 2006); consequently, an accurate contour and extension of dentinal caries lesions cannot be achieved.

With respect to the minimally invasive clinical treatment of caries (Tyas et al., 2000), some of the questions that remain to be answered include the following: “To arrest and remineralize caries lesions, how much bacteria-infected carious dentin should be removed?” “Which dental material can most effectively arrest caries progression and optimize remineralization?” “How much of the demineralizing dentin should be removed to obtain sufficient adhesion of restorative materials?” Without an accurate knowledge of mineral density profiles and lesion extension of dentinal caries, it will not be possible to standardize conservative therapy and assess its consequences.

Conclusions

Over the past decade, significant advances have been made in striving for accurate assessments of the degree of mineralization of calcified tissues by polychromatic CµCT systems. The accuracy, scanning speed, and spatial resolution of µCT systems continue to improve. Although polychromatic µCT is not a substitute for synchrotron µCT, it does provide a user-friendly approach, offering short scanning times and cost-effective CµCT in a laboratory environment.

Based on this review of the application of µCT with polychromatic x-ray sources for mineral density determination, the following conclusions can be drawn:

• The energy spectrum of the x-ray source is fundamentally important to MD determination. Filtration and lowest possible source voltage provide narrow and near-single-peak spectra, favoring high contrast and minimal beam-hardening artifacts; in addition, there is still considerable opportunity for more effective beam monochromatization approaches.

• A precise beam-hardening correction is a critical factor that determines the accuracy of mineral density estimation.

• A simple method to calibrate mineral density is to include two-phase calibration phantoms of appropriate size, covering a representative range of mineral densities of the structure investigated.

CµCT evaluation of mineralization is significant in the context of assessment of human biopsies, animal models, and tissue-engineered bone by polychromatic µCT systems. It is hoped that these recommendations, and the evidence on which they are based, initiate additional discourse and research on the application of µCT with polychromatic x-ray sources for mineral density determination.