Multiple-Timescale Dynamics Underlying Spontaneous Oscillations of Saccular Hair Bundles

Abstract

Spontaneous oscillations displayed by hair bundles of the bullfrog sacculus have complex temporal profiles, not fully captured by single limit-cycle descriptions. Quiescent intervals are typically interspersed with oscillations, leading to a bursting-type behavior. Temporal characteristics of the oscillation are strongly affected by imposing a mechanical load or by the application of a steady-state deflection to the resting position of the bundle. Separate spectral components of the spontaneous motility are differently affected by increases in the external calcium concentration. We use numerical modeling to explore the effects of internal parameters on the oscillatory profiles, and to reproduce the experimental modulation induced by mechanical or ionic manipulation.

Introduction

The sensory epithelium of the inner ear is a remarkably responsive system, capable of detecting displacements due to an incoming sound wave as small as a few Å (1–3). It simultaneously displays a vast dynamic range, covering as much as six orders of magnitude in applied pressure. The detection of mechanical signals by the auditory system is performed by hair cells, named in reference to their ciliated appearance.

Hair cells exhibit highly nonlinear response to external stimuli. The amplification gain is frequency-selective, with each cell maximally responsive at a characteristic frequency, and compressive, with highest gain at low-intensity input. The acuity of auditory detection has been shown to be crucially dependent upon its nonlinearity. In a number of species (4–6), the phenomenon has also been shown to underlie spontaneous limit-cycle oscillations, displayed by individual hair bundles under in vitro conditions.

Theoretical models have proposed that the dynamics of hair bundle response can be described by differential equations that support a Hopf bifurcation (7–10). The equations predict a regime with a stable fixed point, and upon crossing of the bifurcation, the system sustains a stable limit-cycle oscillation. A control parameter determines the dynamic state of the system, with a critical value corresponding to the bifurcation point.

Hair bundles of the bullfrog sacculus oscillate at amplitudes up to ∼100 nm, at 5–50 Hz. We showed previously that these oscillations are mutually uncorrelated, with frequencies uniformly and randomly distributed across the epithelium (11). This study required recording spontaneous motility from hundreds of unloaded bundles to obtain sufficient statistics to characterize their spatial distribution (11,12). We observed that the majority of active hair bundles exhibit multimode oscillations, with long quiescent periods interrupting oscillatory behavior. Reminiscent of bursting behavior seen in neuronal firing patterns (13), this temporal characteristic indicates the existence of an additional manifold with slower dynamics. Prior numerical simulations in the field have described the more regular limit-cycle oscillations (single-mode) observed in hair bundles loaded with an elastic probe (6,14,15). Our data indicate that freely oscillating bundles may access a different dynamics regime, hence, we propose modifications to the models in the referenced literature to describe the observed complex temporal patterns by introducing a variable gating spring element that includes slow calcium-binding dynamics.

Our experiments explore the impact of mechanical and ionic manipulation on the oscillation patterns in hair bundles that exhibit this bursting-type behavior. We show that varying external calcium concentration and imposing a mechanical load affects both the fast component of the oscillations as well as the occurrence of quiescent intervals. We explore these same effects numerically and show that this additional element in the model captures a rich array of experimental observations.

Methods

Experimental techniques

Biological preparation

Experiments were performed on sacculi from North American bullfrog (Rana catesbeiana), proven to be particularly robust to dissection and yielding in vitro preparations that maintain the exquisite mechanical transduction system while allowing sufficient access to measure the responses of individual hair cells (16). Sacculi were excised from the inner ear under cooled and oxygenated saline solutions, then mounted in a two-compartment chamber, with artificial endolymph (117.5 mM K⁺, 2 mM Na⁺, 0.25 mM Ca²⁺, 118 mM Cl⁻, 3 mM D-glucose, and 5 mM HEPES) and perilymph (110 mM Na⁺, 2 mM K⁺, 1.5 mM Ca²⁺, 118 mM Cl⁻, 3 mM D-glucose, 1 mM sodium pyruvate, 1 mM creatine, and 5 mM HEPES) bathing the apical and basal surfaces, respectively. The otolithic membrane was removed with an eyelash tool after the preparation was digested in 50 μg/mL collagenase 1A (Sigma-Aldrich, St. Louis, MO) in artificial endolymph with 4 mM Ca²⁺. For one set of experiments, the concentration of calcium in the endolymph solution was incrementally increased before each recording.

Tracking bundle motility

Hair bundles were imaged on an upright B51X optical microscope (Olympus America, San Diego, CA) under bright-field illumination. Recordings were obtained at 1000 fps with a complementary metal oxide semiconductor (CMOS) camera (FASTCAM SA1.1; Photron, San Diego, CA). Images were analyzed in MATLAB (The MathWorks, Natick, MA), with Gaussian fits to the intensity profiles used to extract the center position of a hair bundle in each frame. A quantity of 5–11 adjacent vertical rows were tracked and averaged for each bundle to enhance the signal/noise ratio of the record. Beads positioned on the epithelium and stationary features within the tissue were tracked to estimate a noise floor of ∼3–5 nm.

Mechanical loading

Mechanical loading was applied to the hair bundles via specially fabricated glass probes. Borosilicate fibers were pulled with a commercial micropipette puller (Model P-97; Sutter Instruments, Novato, CA). A modified microforge was then used to extend an additional thin glass rod from the tip of the fiber, at ∼90° with respect to the axis of taper. The probes were sputter-coated with gold palladium to enhance optical contrast. We recorded their position in water at 10,000 fps and used the power spectra of their random fluctuations for stiffness calibrations. The tips of the glass probes were treated with Concanavalin A—a charged polymer shown to improve adhesion to cells. The fibers were mounted onto a piezo-electric actuator (PiezoJena, Jena, Germany), and positioned with a micromanipulator. Bringing a coated fiber into contact with a hair bundle causes it to adhere: we attached to the kinociliary bulb or the row of tallest stereocilia. The glass probes were used to impose passive loading on selected cells, or to apply steady-state offsets on the resting position of the hair bundles.

Numerical model

We base our numerical model upon previous theoretical simulations of hair bundle mechanics (6,14,15,17–20), and modify it to account for the bursting-type behavior observed in the majority of freely oscillating cells. The limit-cycle instability mainly arises from the interplay between transduction and adaptation, hence its oscillation profile is influenced by the relative dynamics of these two processes. In addition, calcium modulates both of the components, at different timescales.

Hair bundle mechanics

The hair bundle is modeled as a rigid structure with elastic components. The inertial force is neglected, as the system oscillates in a liquid environment (endolymph) at low Reynolds number. The drag force is proportional to the velocity, with drag coefficient ξ. The main contribution to the stiffness of the bundle arises from the pivots of the stereocilia and the tip links, which connect neighboring stereocilia and attach on one of the ends to the transduction channels. These mechanically gated, nonselective ion channels open and close in response to bundle deflection. A schematic diagram of a hair bundle is shown in Fig. S1 in the Supporting Material. We only consider bundle displacement (X) along the axis of sensitivity, corresponding to the direction of increasing height of the stereocilia comprising the bundle. The displacement of the myosin-motor complex along the axis parallel to the stereocilium is denoted by X_a; following convention, the downward direction is defined to be positive. Newton's second law yields the equation of motion for the hair bundle:

$$\xi \frac{dX}{dt}=-N\gamma K_{gs}\left(\gamma X-X_a+X_c-p_{o}d\right)-K_{sp}\left(X-X_{sp}\right)+K_f\left(\Delta -X\right)+\eta .$$ (1)

The first term on the right represents the tension in the gating spring, where N is the number of transduction channels, γ is the geometrical gain for the hair bundle, K_gs is the gating spring stiffness, X_c is the resting extension of the gating spring with all channels closed, p_o is the open probability of the transduction channel, and d is the gating swing distance of the transduction channel. The extension of the gating spring is assumed to be along the stereociliary axis (X_a direction). The second term represents the passive stiffness element of the bundle, with K_sp denoting the combined stiffness of all the connections between adjacent stereocilia, as well as their innate stiffness, determined at their pivots. The offset X_sp is the resting position of an unloaded bundle in the absence of gating springs. The next term accounts for the force exerted by an attached glass fiber, where Δ is the displacement of the fiber base and K_f is the stiffness of the fiber. The noise due to stochastic forces acting on the bundle is denoted by η (see Fluctuations in the System, below).

The transduction channel is described as a two-state system, with its opening probability following the Boltzmann distribution. The energy difference between the open state and the closed state has two contributions: the intrinsic energy difference due to the conformational change (ΔE⁰), and the extension of the gating spring (d). The channel gating is assumed to be instantaneous, and therefore, the open probability is always in equilibrium with the bundle displacement. At temperature T, the open probability of the transduction channel is

$$p_o=\frac{1}{1+\exp \left(\frac{\Delta E^0-K_{gs}d\left(\gamma X-X_a+X_c-d/2\right)}{k_{\text{B}}T}\right)}.$$ (2)

The energy difference ΔE⁰ is determined from Eq. 2 at the resting value of open probability (p_o,0).

Calcium influx

During channel opening, a fraction of the cation inflow is carried by calcium ions, which enter the stereocilia and diffuse to the myosin motors to which they bind. The calcium influx through a transduction channel is well approximated by the Goldman-Hodgkin-Katz current equation (21)

$$I_{Ca}=p_o\frac{P_{Ca}{z}^{2}eF{V}_M{\left[C{a}^{2+}\right]}_{ext}}{k_{\text{B}}T\left(1-\exp \left(\frac{ze{V}_M}{k_{\text{B}}T}\right)\right)},$$ (3)

in which P_Ca is the calcium permeability, z is the valence of the calcium ion, e is the electron charge, F is the Faraday constant, [Ca²⁺]_ext is the calcium concentration in endolymph, and V_M is the membrane potential. We assume the resting calcium concentration inside the stereocilia to be negligible, and thus omit it in our equations. In this model, we assume the membrane potential to be a constant.

The calcium ions diffuse rapidly to the binding sites at myosin motors; therefore, the calcium concentration at the motors is assumed to equilibrate instantly to

$${\left[C{a}^{2+}\right]}_{motor}=\frac{-I_{Ca}}{2\pi zF{D}_{Ca}{r}_m},$$ (4)

where D_Ca is the diffusion coefficient of a calcium ion, and r_m is the distance from the transduction channel to the myosin motors. Following convention, inward current is defined to be negative.

Adaptation

Calcium binding to the myosin motors affects the stability of their actin binding, and allows them to slip along the actin core in response to the force exerted by the gating spring (22,23). The slipping reduces the tension stored in the gating spring and allows the reclosure of the transduction channels. After the calcium ions are instantaneously extruded from the stereocilia during the closed-channel state, the myosin motors restore tension in the gating spring by climbing along the actin filaments.

In the absence of calcium, myosin motors climb along the actin filaments at a constant rate. The slipping rate depends on the tension exerted on the myosin-motor complex by the gating spring, and on the binding of calcium (binding probability p_m). The velocity of the myosin-motor array along the length of a stereocilium is given by

$$\frac{d{X}_a}{dt}=-C+S{K}_{gs}\left[\left(\gamma X-X_a+X_c-p_{o}d\right)-K_{es}\left(X_a-X_{es}\right)\right]+\frac{{\eta }_a\gamma }{{\lambda }_a},$$ (5)

where C is the rate of climbing, S is the rate of slipping, and K_es is the stiffness of the extension spring connecting the myosin motors to the actin core. The resting extension of this spring is given by X_es, and η_a denotes noise similar to η (see Fluctuations in the System, below). For simplicity, the rate of slipping (S) is assumed to linearly depend on p_m. Hence,

$$S=\left(S_{max}-S_{min}\right)p_m+S_{min}.$$ (6)

With the assumption that the dynamics of binding are instantaneous, the binding probability to the motors is given by

$$p_m=\frac{1}{1+\frac{k_{m,off}}{k_{m,on}{\left[C{a}^{2+}\right]}_{motor}}},$$ (7)

with k_m,on and k_m,off denoting the rates of calcium binding and unbinding to the myosin motors. Its resting value (p_m,0) is calculated from Eqs. 3, 4, and 7 at p_o,0. The climbing rate is constant over time but dependent on p_m,0: C = (1 – p_m,0)(C_max – C_min) + C_min.

Slow dynamics

We posit a variable gating spring element, intracellularly in series with the tip link, which consists of a constant spring stiffness in parallel with one of variable stiffness (see Fig. S1 C). Calcium binding to the variable element decreases its stiffness thus rendering the overall gating spring more elastic. For simplicity, we assume the gating stiffness K_gs to linearly decrease with the probability of calcium binding (p_gs),

$$K_{gs}=K_{gs0}-K_{gs1}{p}_{gs},$$ (8)

where K_gs0 is the gating stiffness in the absence of calcium, and K_gs1 is the slope of stiffness change with bound calcium.

This variable gating spring introduced here is analogous to a relaxation element previously proposed to capture fast channel reclosure (9,24). In contrast, the dynamics of calcium binding and unbinding from the variable gating spring are assumed to be slow with respect to those at the myosin motors, and thus introduce a slow timescale into our system. This binding probability follows the standard rate equation

$$\frac{d{p}_{gs}}{dt}=k_{gs,on}{\left[C{a}^{2+}\right]}_{gs}\left(1-p_{gs}\right)-k_{gs,off}{p}_{gs},$$ (9)

with k_gs,on and k_gs,off denoting the rates of binding and unbinding of calcium to the variable gating spring. [Ca²⁺]_gs denotes the calcium concentration at this site. The location of this variable gating spring is assumed to be in close proximity to the myosin motors, and therefore [Ca²⁺]_motor ≈ [Ca²⁺]_gs.

Fluctuations in the system

We incorporate noise terms into our model that were previously shown to play a role in simulated spontaneous oscillations (15). The noise η in the bundle's equation of motion (Eq. 1) accounts for channel clatter and hydrodynamic friction. The noise η_a for myosin displacement (Eq. 5) arises from the force due to the stochastic binding and unbinding of the motors to actin filaments. All the noise terms are assumed to be Gaussian with zero mean, with the fluctuation-dissipation theorem characterizing the autocorrelation function 〈η(t)η(0)〉 = 2 k_BT λδ(t) and 〈η_a(t)η_a(0)〉 = 2 k_BT λ_aδ(t), where λ and λ_a are the friction coefficients of the hair bundle and the myosin motors, respectively, following notations in Nadrowski et al. (15). We neglect any effects of calcium fluctuations.

Simulation protocol

The numerical simulations of Eqs. 1–9 were performed in MATLAB (The MathWorks), using the fourth-order Runge-Kutta method with a time step of 0.1 ms. Table S1 lists all of the parameter values used in the simulations presented. The following criteria were used to distinguish regular from complex oscillations: For a noiseless simulation, regular limit-cycle oscillations (referred to as single-mode oscillation in the figures) have only one channel-opening and closure per cycle, whereas bursting-type ones (referred to as multimode oscillation in the figures) have multiple open and closed states per cycle. The channels are defined as open if the probability p_o exceeds 0.5 and closed otherwise.

Results

Complex temporal profile

The phenomenon of spontaneous motility observed in hair bundles of the amphibian sacculus has been characterized by a limit-cycle oscillation (14). Prior theoretical work has examined the effects of noise on these oscillations, including thermal fluctuations in the ambient water bath, channel clatter, and stochastic binding and unbinding of myosin motors to and from the actin core (15). Incorporating these noise terms into the system of differential equations describing hair-bundle motion captures many of the features experimentally observed in spontaneous oscillations.

Recording with a CMOS camera allows us to track 10–20 hair bundles per field of view, and hence observe spontaneous oscillations in many cells from each preparation. We can then readily record bundle motion without an attached fiber, thus probing its intrinsic oscillation pattern. The top trace of Fig. 1 (Experiment) shows an example of a single limit-cycle oscillation. We observed, however, that the majority of cells display complex temporal profiles, with long pauses occurring intermittently with oscillatory behavior as seen in the bottom trace of Fig. 1 (Experiment). The intervals of quiescence can last hundreds of milliseconds and typically show a slow negative movement of the bundle, indicative of the climbing phase of the myosin.

Figure 1.

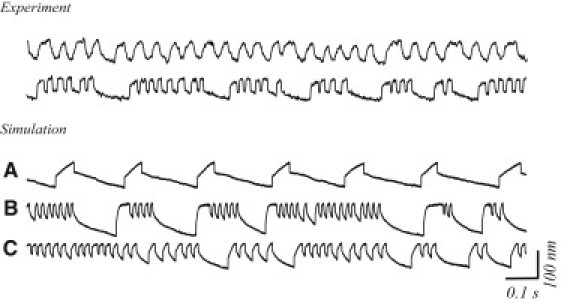
Spontaneous oscillations of hair bundles. Experiment: Time-dependent displacement measured in two different hair bundles. (Top traces) Example of a single-mode oscillation with a single dominant period. (Bottom traces) Multimode oscillation, with oscillatory behavior interspersed with quiescent intervals. (A) Numerical simulation of spontaneous oscillations, with the gating spring stiffness set to be constant. (B and C) Examples of two numerical simulations, which display quiescent intervals interspersed with oscillatory behavior as observed in experimental data. Numerical simulation shown in panel A used the same set of parameters as in panel B, with constant gating stiffness equal to the time-averaged value from panel B.

To capture the intermittent pauses, or multimode oscillatory behavior, we include a variable gating spring—an elastic element of tunable stiffness, hypothesized to be in series with the tip link. We assume the calcium dependence of the variable gating stiffness to be linear. Further, to account for the slow modulation of the oscillatory behavior, we assume the kinetics of calcium binding and dissociation to and from this element to be slow with respect to that of the myosin motor complex (see Methods). Fig. 1, B and C show examples of simulations for two sets of parameters (representing two simulated “cells”) which yield complex oscillatory behavior qualitatively similar to experimental observations. Without the inclusion of the variable gating spring, the multimode oscillation is not observed: Fig. 1 A shows a simulation performed with the same set of parameters as in Fig. 1 B but with a constant gating stiffness, set equal to the time-averaged gating stiffness of the simulation in Fig. 1 B.

In general, a multimode oscillation does not arise in a two-dimensional system as it would show trajectory crossings in a two-dimensional phase portrait. Hence, we introduce a third dimension into the system by including a variable gating spring in the model. An example of a three-dimensional phase portrait of a noiseless multimode oscillation is shown in Fig. 2. The system moves along the trajectory in a clockwise direction from a top-down view: the higher peak of the velocity corresponds to the first opening of the channels after a quiescent interval; the bundle subsequently deflects in the positive direction as myosin motors slip, then, upon channels closing, the bundle position drifts in the negative direction before the channels reopen, corresponding to the lower peak in the velocity. Note that the openings and closings of the channels occur at different positions of the adaptation motors.

Figure 2.

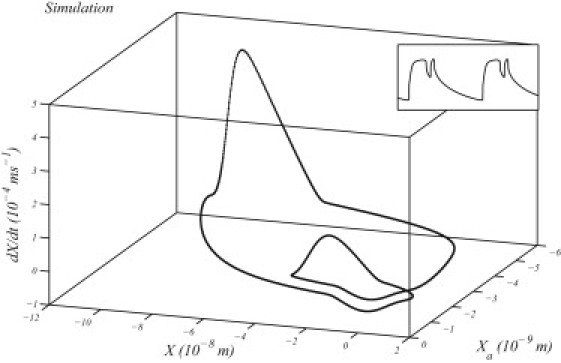
Phase portrait and its projections onto each plane of a simulation of a noiseless multimode oscillation (inset).

In Fig. 3, we show traces from a simulation demonstrating the effects of noise on the active bundle motility predicted by the model. The top traces in Fig. 3, panels A and B, show spontaneous oscillations for two simulated cells, without the inclusion of noise terms. Effects of thermal jitter and stochastic attachment and detachment of myosin motors to and from the actin filaments are introduced into the simulations shown in the bottom traces. As can be seen from the records, noise can strongly affect the oscillation profiles. Fig. 3 A illustrates a case where the addition of noise changed the behavior of a simulated cell from that of regular oscillation to one with sporadic quiescence. For other choices of parameters (example shown in Fig. 3 B), the presence of noise only introduces variation in the timing of the quiescent intervals. This indicates that the bursting-type behavior is sensitive to the choice of model parameters, and is affected by the inclusion of noise terms.

Figure 3.

Simulations of the effects of noise on the oscillation profiles. (Top traces) Simulation of a noiseless spontaneous oscillation. (Bottom traces) Simulations obtained with the same set of parameter values, but with noise terms added. (A) The oscillation becomes multimode in presence of noise, although the noise only causes the irregular occurrence of the quiescent intervals in panel B.

Parameter dependence of multiple oscillatory behavior

With the inclusion of slow calcium dynamics, our numerical simulations capture the bursting-type behavior observed experimentally; the effect was, however, sensitively dependent upon the choice of parameters. We therefore systemically varied key parameters in the simulations without the inclusion of noise terms, to determine the range of values for which the oscillations were single-mode, multimode, or entirely suppressed.

The impact of calcium binding upon the variable gating stiffness and on the myosin motor activity was seen to play an important role in determining the motile behavior. Fig. 4 shows a summary plot, where maximal slipping rate of myosin motors (S_max) and slope of the gating stiffness change with calcium binding (K_gs1) were incrementally varied. As shown in the figure, qualitatively different oscillation profiles were observed in different regimes of the parameter space. Varying these parameters simultaneously is analogous to the experiment in which the calcium concentration in the endolymph is changed, as S_max and K_gs1 describe the calcium sensitivity of the myosin motor complex and the variable gating spring, respectively.

Figure 4.

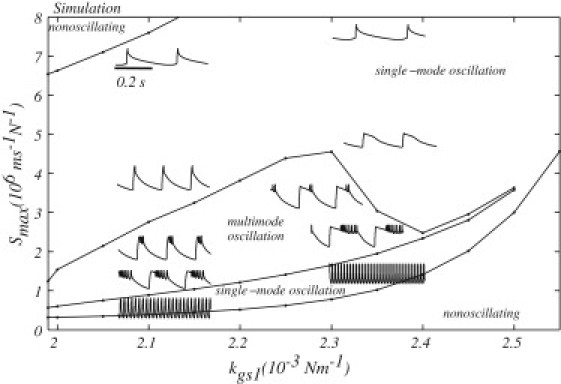
Oscillatory profiles of hair cells over the parameter space of the maximal slipping rate (S_max) and the slope of the stiffness change (K_gs1). The diagram shows various states of the hair bundle: stable (i.e., nonoscillating), oscillating with regular patterns (i.e., single-mode oscillation), or showing complex bursting-type behavior (i.e., multimode oscillation). Examples of the oscillations with different parameter values are shown in the insets located in regions that correspond to their parameters values. The horizontal scale bar indicates 0.2-s time interval for all of the oscillations shown. The displacement of each oscillation is independently scaled. Note that the two nonoscillating regions are due to different stabilities: in the low-S_max region, most of the channels stay open, and in the high-S_max region, most of the channels remain closed. Regimes that show single-mode oscillation likewise show different patterns, though no sharp transition exists at high K_gs1. The region with S_max higher than that of the multimode oscillation region shows spikelike profiles with periodicity determined by the quiescent interval and the region with lower S_max shows only fast component of the oscillations.

In Fig. 5, we plot the results of a numerical study where the stiffness of the stereociliary pivots (K_sp) and the offset position of the bundle due to the stereociliary pivots (X_sp) were systematically varied in the model. The steady-state terms were found to have a profound effect upon the oscillation profiles, as illustrated in the diagram. These numerical results are consistent with our experimental observations (L. Fredrickson-Hemsing, S. Ji, R. Bruinsma, and D. Bozovic, unpublished), where imposed offsets were shown to modulate and even suppress spontaneous oscillations in hair bundles (example shown later in Fig. 8). This parameter space also corresponds to the experiment where the overall stiffness of the bundle is manipulated by imposing a mechanical load on the bundle (examples shown later in Fig. 9).

Figure 5.

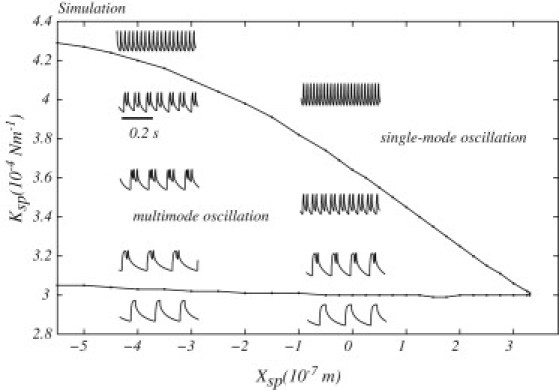
Oscillatory profiles of hair cells over the parameter space of the stiffness (K_sp) and offset (X_sp) of the stereociliary pivots. The diagram determines the multimode oscillation and single-mode oscillation states of the hair bundle, as in Fig. 4. Examples of oscillations are illustrated in the insets located in the areas corresponding to their parameter values with the same scale bar indicating 0.2-s time interval. The single-mode oscillation region with high K_sp shows only fast oscillations, whereas the single-mode oscillation region with low K_sp shows oscillations with a dominant slow period.

Figure 8.

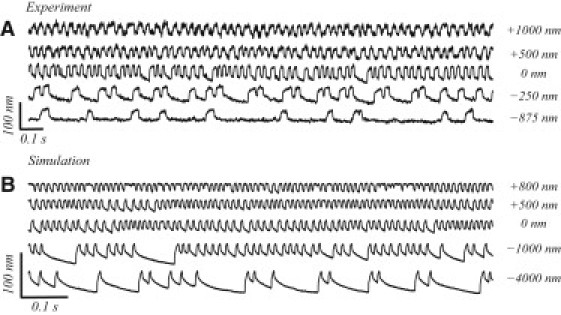
Effects of steady-state offsets imposed on an oscillating hair bundle. (A) Experimental records, where constant deflections were imposed on the bundle via a glass probe of stiffness 100 μN/m. (B) The corresponding numerical simulation. For offsets in the positive direction, the oscillations are faster and smaller and the quiescent intervals disappear. In the negative direction, however, the quiescent intervals occur more frequently and eventually become the dominant component of the oscillation profile.

Figure 9.

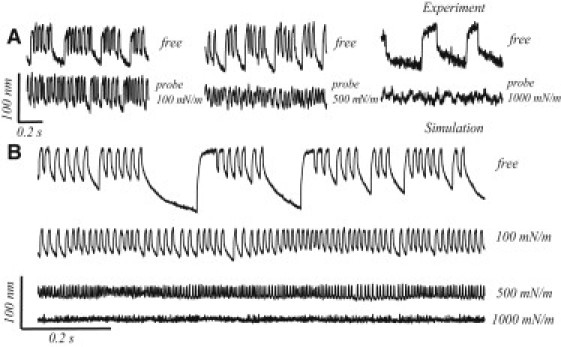
Effects of mechanical loading, obtained experimentally (A) and theoretically (B). The top traces in each of the panels in A represent the oscillation profiles of free bundles. Upon light loading, 100 μN/m, the quiescent intervals disappear (A, left); with an intermediate load, 500 μN/m, the oscillations become fast and small (A, middle); heavy loading, 1000 μN/m, finally suppresses the oscillation (A, right). The simulations of hair bundle oscillations under the same set of loading conditions captures the full range of behavior (B).

In Fig. 6, we plot the time evolution of key parameters (X, p_m, and p_gs) during a simulated multimode oscillation. We find that the transduction channel's opening probability varies through most of its full range during the fast component of the oscillation. Probability of calcium binding to the myosin motors (Fig. 6 B) likewise shows the full range of modulation. Binding probability to the variable gating spring, on the contrary, shows only partial modulation during the fast cycles (as seen in Fig. 6 C). Consistent with the imposed slow dynamics, modulation reaches its full extent only over the slower timescales that include the quiescent intervals.

Figure 6.

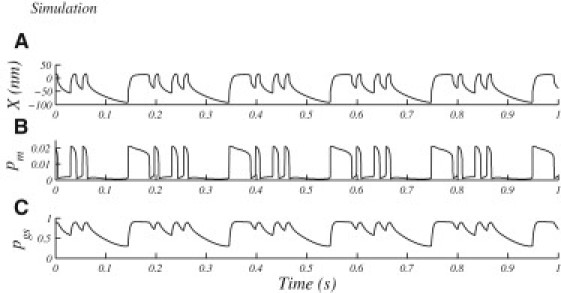
Plots of the parameter variation from the simulation of a noiseless oscillation shown in Fig. 2B. (A) The position of the hair bundle (X). (B) The probability of calcium binding to the myosin motors (p_m). (C) The probability of calcium binding to the variable gating spring (p_gs). Notice that the decay of p_gs during channel-closed state is significantly slower than that of p_m, illustrating the slow dynamics of calcium binding at the variable gating spring.

Effects of external calcium concentration

Previous experiments have shown calcium to have a strong effect on the active motility of hair bundles: increasing its concentration in endolymph causes a reduction in the amplitude and an increase in the frequency of spontaneous oscillation (6,26). We measured the effects of this ionic manipulation on motile hair bundles that displayed multimode oscillatory pattern. The faster component of the oscillation showed an increase in the characteristic frequency. Notably, the duration of the open channel state was more strongly affected than that of the closed state, resulting in a spikelike profile. The duration of the quiescent intervals were, on the contrary, only slightly shortened by the increase in calcium. Fig. 7 A shows an example of measurements in which the concentration of calcium in endolymph solution was incrementally raised; Fig. 7 B shows numerical simulations under the same conditions. As can be seen from the traces, the model captures the impact of the ionic manipulation on both the fast and slow components of the oscillation profile.

Figure 7.

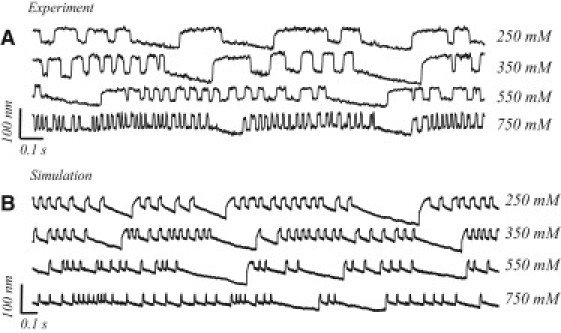
Effects of calcium concentration in the endolymph upon characteristics of the oscillation. (A) Experimental records of spontaneous motility obtained from the same hair bundle under four different calcium concentrations: 250, 350, 550, and 750 μM. (B) Numerical simulations under the same calcium concentrations as in the experiment. Both display similar effects: at higher concentration, the fast component of the oscillation becomes faster and smaller in amplitude, whereas the slow component does not show a significant change.

Steady-state offsets imposed on the bundle position

Mechanical offsets imposed on the resting position of the bundle were seen to strongly affect its oscillatory behavior. In a recent study (L. Fredrickson-Hemsing, S. Ji, R. Bruinsma, and D. Bozovic, unpublished), we showed that a slow ramp in the offset position can serve as a dynamic parameter that tunes the frequency of spontaneous oscillation and induces a bifurcation crossing from oscillatory to the quiescent state. Fig. 8 A shows the results of an experiment in which steady-state offsets was imposed on a bundle with a flexible glass fiber, and Fig. 8 B shows the accompanying numerical simulation. Consistent with the experimental observations, deflections in the negative direction reduce the number of oscillations during each burst and extend the duration of the quiescent intervals. Deflections in the positive direction, on the contrary, eliminate the quiescent intervals and result in single-mode oscillations. This behavior is also illustrated in Fig. 5 which examines numerically effects analogous to the imposed offsets. Positive steady-state deflections shift the system from the multimode oscillation to single-mode oscillation regime. Moderate negative offsets maintain bursting-type behavior while increasing the duration of the quiescent interval. Further offsets eliminate the short-period component of the oscillations, leading to a single-mode oscillation with a spikelike pattern.

Stiffness of the mechanical load

Multimode oscillations are more often observed in unencumbered bundles than those under an external load. In Fig. 9 A, we illustrate three measurements of spontaneous bundle motility before and after the attachment of a glass probe. With light loading, the occurrence of quiescent intervals was reduced, whereas the higher-frequency components remained unchanged (Fig. 9 A, left). Stronger loading led to a reduction in the amplitude and an increase in the characteristic frequency of oscillation, and eliminated the occurrence of quiescent intervals (Fig. 9 A, middle). Further increase in the stiffness of the load (Fig. 9 A, right) led to a near-suppression of innate oscillations. Fig. 9 B displays the numerical simulations corresponding to these experiments. The stiffness of the attached load (K_f in Eq. 1) was incrementally increased in the calculation to capture the full range of effects. The numerical simulations reproduce all the main features of the experimental data: quiescent pauses are suppressed, the oscillation frequency increases, and the amplitude decreases. This is analogous to an increase in the parameter K_sp, leading to a crossing from multi- to single-mode oscillatory regimes, shown in Fig. 5.

Discussion

Direct gating of transduction channels in the stereocilia has been established as the fundamental mechanism behind mechanosensation in hair cells. Tip links connecting neighboring stereocilia were proposed to comprise the gating spring and introduced into numerical models to explain the nonlinear mechanical response (27,28). Recent molecular dynamic simulations indicated, however, that the tip link itself is far too stiff to constitute the putative gating spring (29). Because the structural integrity of the tip link and its connection to the transduction channel is crucial for the proper detection of sound (1), it must constitute one of the elements of the full mechanoelectrical transduction complex. An elastic element in series with the tip link would be consistent with both sets of results.

The numerical model presented here incorporates a variable gating spring, composed of a spring of constant stiffness in parallel with one of calcium-dependent compliance. Because there are 30–50 stereocilia in a hair bundle, each with a gating spring, and potentially multiple calcium-binding sites on each element, the linear term constitutes the simplest mean-field approximation for the calcium-dependent stiffness of the gating spring. Possible cooperativity of calcium binding to multiple sites on the variable gating spring is not considered in this model. Also note that the variable gating spring might be interpreted as any spring element within a bundle that regulates the degree of nonlinearity of the system.

The dynamics of calcium association and dissociation from the proposed variable gating spring are assumed to be slow with respect to other timescales in the system, most notably that of the myosin motor activity. Introduction of a slow dynamic into our model allowed us to reproduce the complex temporal patterns, observed in hundreds of spontaneous oscillations recorded in the course of these experiments.

To characterize the factors determining the temporal profiles of spontaneous motility, we explored the space of key parameters in the model and classified the resultant oscillations. We found a strong dependence on calcium sensitivity of the variable gating stiffness and on the rate of myosin-based adaptation. Hence, any cellular mechanism that would fine-tune the internal calcium concentration would affect the steady-state gating spring stiffness and thus have a strong impact on the oscillation dynamics. Ion channels found in the hair cell soma were shown to form an electronic circuit that can exhibit resonance, tuning, and spontaneous voltage oscillations (30,31). In a previous publication (32), we showed that inhibiting or modulating the activity of the somatic system qualitatively changed the temporal profiles of the spontaneous mechanical oscillations of the bundle. Somatic ion channels comprise a possible control system via the membrane potential that could modulate internal calcium levels and thus affect the variable gating stiffness (20).

Offsets imposed on the resting position of the bundle or of the adaptation motors were seen to profoundly influence oscillation characteristics in the simulations. This is consistent with our experimental findings that steady-state deflections can regularize, modulate, or entirely suppress spontaneous oscillations (L. Fredrickson-Hemsing, S. Ji, R. Bruinsma, and D. Bozovic, unpublished). The effects of calcium and steady-state mechanics may be interlinked in the hair cell, with offsets in the bundle position introduced by stiffening or softening of internal gating elements, modulated in turn by calcium binding.

Conclusion

We propose what we believe to be a new element in the numerical model of hair cell mechanics to account for the occurrence of bursting-type behavior in spontaneously oscillating bundles. The gating spring is stipulated to contain a variable-stiffness element, dependent upon calcium binding. Importantly, the dynamics of calcium association and dissociation to and from the variable element are assumed to be slow with respect to those modulating the slipping rate of the myosin motor complex. The model reproduces the complex temporal patterns observed in spontaneously oscillating hair bundles, including the occurrence of multimode oscillations.

Calcium concentration in the endolymph solution bathing the apical side of the preparation was seen to strongly affect the frequency and amplitude of the fast component of the oscillation, but only weakly modulate the duration of the quiescent intervals. Steady-state offsets on the bundle position induced a crossing from multi- to single-mode oscillations with positive and negative deflections affecting the bundle asymmetrically. Finally, an imposed mechanical load was seen to reduce the occurrence of quiescent intervals, leading to a more regular oscillation pattern, eventually fully suppressing the oscillation. The full set of experimental findings were reproduced by the numerical model with the single addition of a slowly-varying, calcium-dependent variable gating spring.