Figure 3.

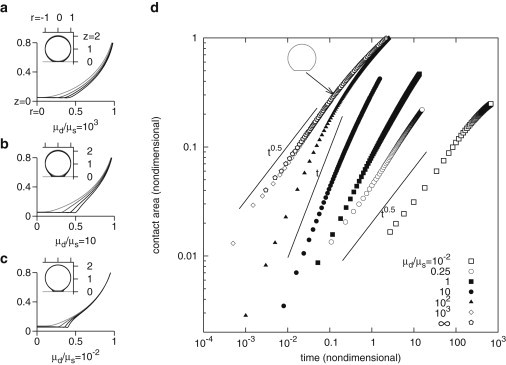
Initial drop spreading obeys power-laws that depend on viscosity contrast. (a–c) Shape evolution for different viscosity contrasts ${\mu }_d/{\mu }_s$, in $\left(r,z\right)$ coordinates. Insets, global view (negative values of r are drawn by symmetry), main plots, close-up next to substrate. Gray levels correspond to regularly spaced time intervals, from light to dark. (a), for ${\mu }_d/{\mu }_s={10}^3$ the drop deformation is minimized, this is also the case for higher viscosity contrasts and corresponds to a spreading profile $A\propto t^{0.5}$. Identical evolution is obtained for any ratio ${\mu }_d/{\mu }_s\ge 500$. (b), for ${\mu }_d/{\mu }_s=10$ the drop deforms to allow efficient drainage of the medium, this corresponds to a spreading profile $A\propto t$. Identical evolution is obtained for any ratio $2\le {\mu }_d/{\mu }_s\le 20$. (c), for ${\mu }_d/{\mu }_s={10}^{-2}$ the drag on the drop is very high and spreading occurs through local deformations only, the top part of the drop is nearly immobile (inset). Identical evolution is obtained for any ratio ${\mu }_d/{\mu }_s\le 0.5$. (d) Growth of aligned area of drops is shown as a function of time for different viscosity contrasts. Power-law initial spreading rates are clearly identified, behaving as t or $t^{0.5}$ depending on the viscosity contrast. For area $A\gtrsim A_{drop}^{\ast }=0.3A_0$, the rate is lower. Inset shows the shape of a viscous drop in the void (viscosity contrast infinite) for $A_{drop}^{\ast }=0.3A_0$ (arrow).