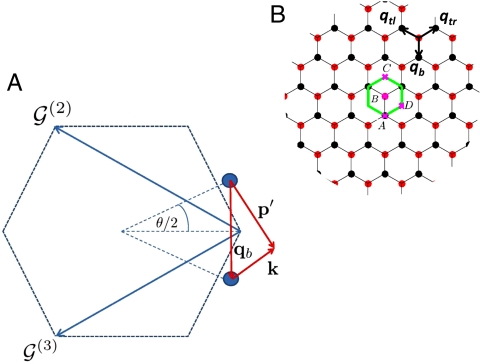
Fig. 1.

Momentum-space geometry of a twisted bilayer. (A) Dashed line marks the first Brillouin zone of an unrotated layer. The three equivalent Dirac points are connected by 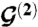and 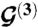. The circles represent Dirac points of the rotated graphene layers, separated by k_θ = 2k_D sin(θ/2), where k_D is the magnitude of the Brillouin-zone corner wave vector for a single layer. Conservation of crystal momentum implies that p^′ = k + q_b for a tunneling process in the vicinity of the plotted Dirac points. (B) The three equivalent Dirac points in the first Brillouin zone result in three distinct hopping processes. Interference between hopping processes with different wave vectors captures the spatial variation of interlayer coordination that defines the moiré pattern. For all the three processes |q_j| = k_θ; however, the hopping directions are (0,-1) for j = 1, 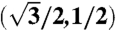for j = 2, and 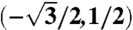for j = 3. We interchangeably use 1, 2, 3, b, tr, and tl as subscripts for the three momentum transfers q_j. Repeated hopping generates a k-space honeycomb lattice. The green solid line marks the moiré band Wigner–Seitz cell. In a repeated zone scheme the red and black circles mark the Dirac points of the two layers.