Table 2.

BSA and FFT results from simulated harmonic data with noise and background trends

No.	ω	ea (%)	ep (%)	b		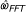σFFT		σBSA		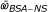σBSA-NS	s-n
1	0.5	1	-	-	0.49	0.06	0.5	0	0.5	0.0002	70
2	0.5	10	-	-	0.49	0.20	0.5	0.0002	0.5	0.0004	6.5
3	0.5	40	-	-	0.49	0.54	0.5	0.0005	0.5	0.0011	1.9
4	0.5	10	10	-	0.49	0.27	0.5	0	0.5	0.0003	4.2
5	0.5	10	40	-	0.49	0.57	0.5	0.0002	0.5	0.0007	2.2
6	0.5	100	40	-	0.49	0.89	0.5	0.0006	0.5	0.0020	0.7
7	0.3, 0.5	10	10	-	0.29, 0.51	0.14	0.3, 0.5	0.0003	0.34	0.0832	1
8	0.5	10	-	-t	0	0.15	0.5	0.0002	0.5	0.0002	110
9	0.5	10	-	-t2	0	0.19	0.5	0.0002	0.5	0.0002	90
10	0.5	10	-	-t3	0.02	0.24	0.5	0.0003	0.5	0.0002	35

Each time series was generated with a sine function of angular frequency, ω, of 0.5 rad/s with a level of noise in amplitude, e_a, and phase, e_p. In some time series a background trend (b) was included, and in case number 7 an additional sine function of 0.3 rad/s is present. The resulting function was sampled 200 times at an interval of 1 s. Results from FFT are presented in the form of the angular frequency with the highest power, 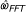, and the estimated standard deviation, σ_FFT. The Bayesian frequency estimate at the maximum posterior point is denoted by and its standard deviation by σ_BSA. For comparison, the expectation value of ω and its standard deviation computed using BSA and Nested Sampling (BSA-NS) are denoted by 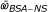and σ_BSA-NS. Values of σ below 10^-8 are listed as 0. The estimated signal-to-noise ratio (s-n) from the Bayesian analysis is given in the last column. The BSA and BSA-NS approaches deliver the same results, apart from the case of multiple frequencies in a 1D search of ω (case No. 7), which for BSA-NS leads an intermediate estimate between the frequencies with a higher standard deviation.