Disaccharide Binding to Galectin-1: Free Energy Calculations and Molecular Recognition Mechanism

Abstract

Galectin-1, a member of the conserved family of carbohydrate-binding proteins with affinity for β-galactosides, is a key modulator of diverse cell functions such as immune response and regulation. The binding affinity and specificity of galectin-1 for eight different β-galactosyl terminal disaccharides was studied using molecular-dynamics simulations in which the ligand was pulled away from the binding site using a mechanical force. We present what we believe to be a novel procedure, based on combinations of multistep trajectories, that was used to estimate the binding free energy (ΔG) of each disaccharide. The computed binding free energy differences show excellent correlation with experimental values determined previously. The small differences in affinity among the disaccharides are the result of an exquisite balance between the strengths of the galectin-sugar H-bonds and the H-bonds the protein and the disaccharides make with the solvent. Analysis of the free energies along the reaction coordinate shows that disaccharide unbinding/binding presents no energetic barrier and, therefore, is diffusion-limited. In addition, the calculations revealed that as the ligand is undocked from the binding site, breaking of protein-disaccharide H-bonds takes place in stages with intermediate states in which the interactions are bridged by water molecules.

Introduction

Protein-carbohydrate interactions are key to biological processes including cellular and molecular recognition, innate immunity, adhesion, and migration (1). Thus, it is of fundamental importance to understand, in molecular detail, the mechanisms determining the affinity and the specificity of these interactions. The structural complexity of glycans that results from differences in their chemistry and their sequences, as well as from their ability to form branched polymers (2), creates a highly diverse set of information encoding molecules (3,4).

Galectins are an important family of carbohydrate recognition proteins characterized by a conserved sequence in the carbohydrate recognition domain (CRD) and by a high affinity for β-galactosides (5). They are soluble proteins that play a key role in intra- and extracellular processes such as cell-cell and cell-matrix interactions, apoptosis, growth control, tumor spread, innate immunity, immune response, host pathogen recognition, cytokine, and mediator secretion and chemoattraction (5). To regulate these cellular functions, galectins act by binding to glycan ligands of glycoprotein receptors on the cell surface. Thus, as key modulators of a variety of cell functions, galectins have emerged as an important drug target, particularly in cancer therapy (6,7). Galectins have been identified in species ranging from nematodes to mammals (for reviews, see (1,8)). So far, 16 members of the galectin family have been identified in mammals. Galectins 1–16 exhibit structural differences that led to further classification into three groups:

• 1.Galectins-1, -2, -5, -7, -10, -11, -13, and -14 have one CRD and can exist as monomers or noncovalent dimers.
• 2.Galectins-4, -6, -8, -9, and -12 have two CRDs in each domain.
• 3.Galectins-3 are chimeric proteins composed by a CRD domain and a nongalectin domain.

Galectin-1, a ubiquitous member of the galectin family, binds preferentially N-acetyllactosamine but can also accommodate a variety of β-galactosamides with modifications in the nonreducing end, the glycosidic linkage, or even longer oligosaccharides (9–12). Galectin-1 functions as a noncovalent homodimer (10) in which each monomer is formed by 11 antiparallel β-strands forming a β-sandwich, with one CRD per monomer. The galectin-1 CRDs contain the following residues: His-44, Asn-46, Arg-48, His-52, Asn-61, Trp-68, Glu-71, and Arg-73 (Fig. 1). Galectin-1 is one of the master regulators of different stages of the immune response including T-cell survival and cytokine secretion in autoimmune diseases, transplantation, and parasitic infections (1). Elevated expression of galectin-1 has been observed in certain types of cancers in which an immunosuppressive environment is created by the negative regulatory action of galectin-1 over activated T-cells (6,13). Participation of galectins in these and other key physiological processes points to these proteins as potential therapeutic targets.

Figure 1.

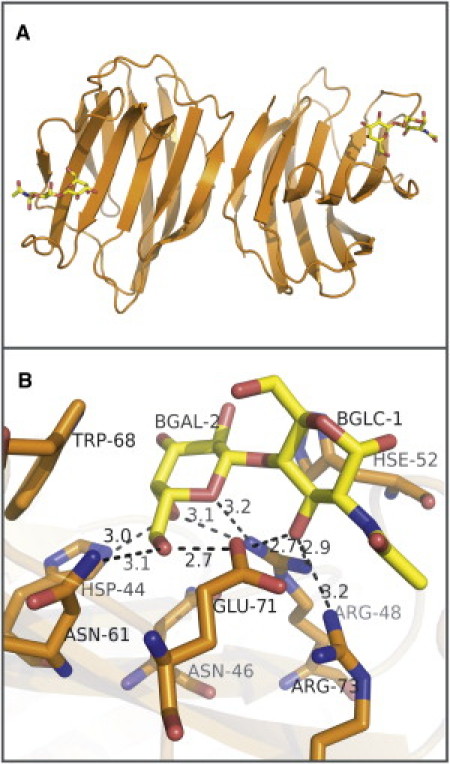
Crystal structure of bovine galectin-1/Gal(β1-4)GlcNAc complex. (A) Representation of the galectin-1 homodimer bound to Gal(β1-4)GlcNAc (PDB ID 1SLT). (B) Galectin-1 binding site representation. (Sticks) Residues of the CRD and disaccharide. (Dashed lines) H-bonds. One water molecule, conserved in the binding site, participates in a bridged interaction between the protein and the ligand.

Thermodynamic studies have shown that galectin-disaccharide binding reactions are primarily enthalpically driven but exhibit enthalpy-entropy compensation (14). Isothermal titration calorimetry (ITC) data on galectin-1/sugar complexes suggests that a large percentage of the observed binding enthalpy arises from dynamic reorganization of water molecules, including transfer of protein-bound water molecules to bulk solvent (15–17). Structured water molecules play a fundamental role at the binding site of galectins: x-ray diffraction studies of complexed and uncomplexed galectins show that H-bonds between the protein and water molecules are exactly replaced after binding by those formed by the carbohydrate hydroxyl groups (18).

Consistent with these data, molecular-dynamics (MD) studies have identified water sites in the galectin-1 CRD that correlate with the position of the carbohydrate hydroxyl groups in the bound state (19,20). Upon unbinding the sugars, substantial water reorganization takes place in the binding site, with exchange of protein-ligand interactions by ligand-solvent and protein-solvent interactions. NMR studies have shown that binding of a lactose-derived disaccharide to galectin-1 results in substantial water reorganization, changing the polar environment of Trp-68 (21). Even though no major conformational change occurs, it has been reported that, upon lactose binding, galectin-1 flexibility increases—resulting in access to a larger number of conformations (22).

In this article, we report an investigation of the binding of eight different disaccharides to bovine spleen galectin-1, using the multistep computational process introduced by Echeverria and Amzel (23). In this protocol, to undock the ligand from the binding pocket and estimate the free energy of binding, the system is driven from a bound state A to an unbound state B in a series of steps along a reaction coordinate. During these steps, the system can sample nonequilibrium conformations, but at discrete intervals the system is allowed to equilibrate. Exchange of trajectories between these equilibrated states is used in a combinatorial way to build a work-probability distribution. This distribution, in conjunction with Jarzynski's equation (24,25), is used to compute the free energy of the process. The computed free energies we obtained are in excellent agreement with experimental data for binding of the disaccharides (14). The trajectories computed to calculate these free-energies reveal molecular details of the unbinding process that provide mechanistic insight into the affinity and specificity of carbohydrate binding.

Methods

System setup and initial conditions

We analyzed the complexes of galectin-1 with each of the following disaccharides: N-acetyllactosamine (Gal(β1-4)glcNAc), lactose (Gal(β1-4)Glc), methyl β-lactoside (Gal(β1-4)Glcβ-OMe), 2′-O-methyllactose (MeO-2Gal(β1-4)Glc), 4-O-β-D-galactopyranosyl-D-mannopyranoside (Gal(β1-4)Man), lactulose (Gal(β1-4)Frp), 3-O-β-D-galactopyranosyl-D-arabinose (Gal(β1-3)Arp), and lacto-N-biose (Gal(β1-3)GlcNAc) (see Fig. S1 in the Supporting Material). A crystallographic structure is available for only one of these complexes: the bovine spleen galectin-1 (also called “S-lectin”) in complex with the disaccharide N-acetyllactosamine (Gal(β1-4)glcNAc) determined at 1.9 Å resolution (PDB accession code 1SLT) (10) (Fig. 1).

Models of the other seven complexes were built using the crystallographic structure of the galecin-1/Gal(β1-4)glcNAc complex and the internal coordinates of the sugars obtained from the geometry defined in the carbohydrate force field (26). The galactose ring of each disaccharide was placed by overlapping it with the equivalent ring in the x-ray structure. The orientation of the second hexose was determined by defining the same dihedral glycosidic angles as Gal(β1-4)GlcNAc and allowing the structure to relax by minimization and equilibration dynamics.

All simulations were performed using the program CHARMM with the CHARMM27/CMAP force field for proteins (27), and the CHARMM35 parameters for carbohydrates (26). In the MD simulations, only one of the two equivalent crystallographic monomers with its disaccharide ligand was used. The model includes 133 protein residues, one disaccharide, the crystallographic water molecules, and a box of TIP3 water molecules of dimensions 49.67 × 52.77 × 43.46 Å (∼3808 TIP3 water molecules). Periodic boundary conditions were used in all calculations and long-range electrostatics were treated with particle-mesh Ewald summation. All calculations were carried out using an integration step of 1 fs. The SHAKE algorithm was applied to all hydrogen-containing bonds. Simulations were performed in a microcanonical ensemble, for which the energy of the system is kept constant.

The initial system was first minimized for 4000 steps using steepest-descent and conjugate gradient methods. After minimization, the system was heated gradually to 298 K (30 ps) and equilibrated for 70 ps.

Simulation protocol

Starting from the minimized and preequilibrated model, individual trajectories were initiated by assigning random velocities with a Maxwell distribution at 298 K to all atoms. These systems were further equilibrated for 40 ps before starting the unbinding simulation in which the disaccharide was mechanically pulled away from the protein. To apply the pulling force, a dummy atom was introduced at the center of mass of the ligand. Three atoms of the disaccharide were simultaneously tethered to the dummy atom—the two carbons involved in the glycosidic linkage and the glycosidic oxygen. The force constant for each tether was set to 10 kcal/Ų mol (dummy atom to carbon atom distance: 1.5 Å; dummy atom to oxygen atom distance: 1.2 Å). The dummy atom was used during simulations to pull the disaccharide from the binding site. To avoid rotations and tilting of the disaccharide while unbinding, the pulling axis was defined as the second axis of inertia of the disaccharide molecule (Fig. S3). Using the largest axis of inertia would have resulted in clashes between the protein and the ligand during the pulling process.

Each of the three tethers between the disaccharide and the dummy atom was treated as a harmonic constraint such that the force is given by

$$\overrightarrow{F}=-k\left({\overrightarrow{r}}_X-{\overrightarrow{r}}_{ref}\right),$$

where ${\overrightarrow{r}}_X$ is the position of the atom attached to the dummy atom and ${\overrightarrow{r}}_{ref}$ corresponds to the position of the target at the equilibrium point of the each harmonic constraint (i.e., 1.5 Å from the dummy atom for carbons and 1.2 Å for the oxygen). The force on the disaccharide was calculated by considering the deformation of each tether. The effective force constant, when projecting the contribution of each spring onto the direction of the pulling axis, is ∼7 kcal/Ų mol. The work contribution of each of the three atoms attached to the mobile dummy atom at step N is given by

$$W={\int }_{r_{X,N}}^{r_{X,N+1}}\overrightarrow{F}\cdot d{\overrightarrow{r}}_X,$$

where $\overrightarrow{F}$ is the force projected onto the pulling axis and $d{\overrightarrow{r}}_X$ is the differential along the pulling direction. The total work is the sum of the contributions of the three tethers. The deformations of the disaccharide covalent bonds are equivalent to those in the simulations of the free disaccharide in water (see below) and have no net component in the direction of movement.

The sugar was pulled away from the protein's binding site using a combination of translations of the dummy atom followed by equilibrations of the system as described before (23). The dummy atom was pulled in steps of 0.1 Å. After each step, the system was allowed to equilibrate for 2.5 ps. Hereafter these are referred to as “small-steps”. When 10 small-steps were completed, equivalent to a 1 Å extension, the system was equilibrated for 50 ps. This will be referred to as a “long-step”. Each set of eight long-steps, equivalent to translating the disaccharide 8 Å from the binding site, constitutes a trajectory.

MD simulations (3 ns) of free disaccharides were performed in a TIP3 water box to gauge the flexibility of the disaccharide in solution. These pulling simulations of the disaccharide in the absence of the protein were performed for different tether force constants and pulling velocities. These control simulations were used to select the strength of the harmonic-constraint force-constant of the tethers between the dummy atom and the disaccharide such that geometry of the sugar was not distorted during the pulling process. In addition, the pulling velocity was adjusted so that the average work done to pull the disaccharide in water was zero.

Free energy calculations

For each galectin/disaccharide complex, 28 trajectories were computed. The number of trajectories needed was selected so that the free energy estimates for each of the disaccharides converged with an error of <0.3 kcal/mol (28,29). Free energies were estimated with the multistep trajectory combination (MSTC) method (23). The method is based on recognizing that for different trajectories, equilibrium microstates at the end of each long-step belong to the same ensemble, and therefore new trajectories can be built by combining long-steps of different trajectories at the equilibration points. Two equivalent approaches were used to estimate the ΔG of the transition. In the first approach, individual and ordered 1 Å steps (1– 8) were randomly selected from each of the 28 trajectories until a new trajectory was built. For each disaccharide/galectin-1 system, 10⁷ trajectories were generated that were used to generate the work probability distributions P(W). With these probability distributions, Jarzynski's equality was used to calculate the free energy as

$$\Delta G=-{\beta }^{-1}\ln \left(\langle e^{-\beta W}\rangle \right),$$

(with β = 1/kT) (24,25). This exponential average of the work heavily weights low energy values (Fig. S3). The values of ΔG can also be calculated for the n^m (28⁸; n = 28 and m = 8) trajectories using the expression

$$\Delta G=-{\beta }^{-1}\sum _{i_s=1}^m\ln \frac{1}{n}\sum _{i_t}^n{e}^{-\beta W_{i_t,i_s}},$$

where i_t is the trajectory number and i_s is the long-step number (23). This expression is equivalent to the sum of the Jarzynski averages carried out for each long-step over all trajectories,

$$\Delta G=\sum _{j=1}^8\Delta G_j,$$

where ΔG_j is the Jarzynski average of each long step.

The exponential average over many trajectories of the work needed to move the ligand from the binding site to the bulk solvent corresponds to the ratio of the partition functions of the hydrated complex and the separately hydrated protein and ligand (24,25). This is

$$\langle e^{-\beta W}\rangle =\frac{Z_1}{Z_0}=\frac{Z_{P+L}}{Z_{P\cdot L}},$$

where Z_P·L is the partition function for the system with the ligand bound, whereas Z_P+L is the partition function of the system when the ligand is unbound. Because

$$\Delta G=-{\beta }^{-1}\ln \left(\frac{Z_1}{Z_0}\right),$$

the free energy is determined by a dimensionless ratio of partition functions. As a result, no dimensional correction is needed for the free energies values reported.

MD trajectory analysis

Different aspects of each trajectory were monitored during the disaccharide pulling simulations. Total energy and potential energy were analyzed every 0.25 ps to evaluate how well equilibrated the system was at the end of each long-step. The van der Waals and electrostatic interaction energies were monitored between ligand and protein and between ligand and solvent. Direct H-bonds and those bridged by one TIP3 water molecule were identified using a 3.0 Å distance cutoff. In addition, glycosidic torsion angles ϕ and ψ for the 1-n linkage, defined as

$$\varphi ={\mathrm{O}}_5–{\mathrm{C}}_1–{\mathrm{O}}_{\mathrm{n}}–{\mathrm{C}}_{\mathrm{n}}\mathrm{and}\psi ={\mathrm{C}}_1–{\mathrm{O}}_{\mathrm{n}}–{\mathrm{C}}_{\mathrm{n}}–{\mathrm{C}}_{\mathrm{n}-1},$$

were analyzed during the pulling simulations.

Results and Discussion

Disaccharide flexibility: MD of free disaccharide

During the undocking simulations, it is expected that combining soft tethers to the dummy atom with long equilibration periods at the end of each long-step allows the system to relax, and so avoid deformations caused by stress in the disaccharide glycosidic bond. To verify that the presence of the tethers does not introduce a conformational bias, different aspects of the glycosidic bond flexibility with the free and the tethered disaccharides were analyzed.

Ramachandran-like plots for the glycosidic angles ϕ and ψ similar to those reported before (30) were calculated for the eight disaccharides. Fig. 2 shows that, for the disaccharide Gal(β1-4)glcNAc, there are three favorable ϕ and ψ combinations. The ϕ- and ψ-angles sampled by free Gal(β1-4)glcNAc during the MD simulation (in a box of TIP3 water) correspond to only one of these minima (Fig. 2 B, dots), which is ∼2 kcal/mol lower in energy than the other minima. This minimum, which contains most of the low energy states of the Gal(β1-4)glcNAc, has mean values of ϕ and ψ of 131° and −84°, with RMS deviations of 5° and 8°, respectively.

Figure 2.

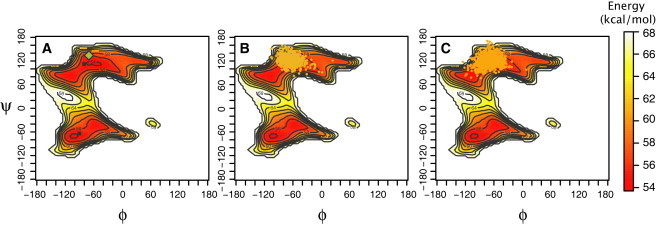
Gal(β1-4)GlcNAc ϕ- and ψ-dihedral angles distributions. (A) Ramachandran plot for glycosidic torsion angles ϕ and ψ. Maps present the energy as a function of the given angles. (Diamond) The ϕ and ψ combination of the crystal structure conformation. (B) Same as panel A, but showing ϕ and ψ combinations sampled by the free disaccharide in solution (dots). (C) Same as panel A, but showing the ϕ and ψ combinations sampled by the disaccharide when attached to a dummy atom and pulled in a water box (dots).

The dummy atom does not restrict the flexibility of the glycosidic bond: when it is bound to the free disaccharide, the average ϕ- and ψ-angles are 130° and −85°, with RMS deviations of 7° and 8°, respectively. Furthermore, the ϕ- and ψ-angles sampled as the disaccharide is pulled in water (no protein) (Fig. 2 C, dots) show that the conformational sampling is restricted to the same region of the Ramachandran plot observed for the free disaccharide, with mean values of the ϕ- and ψ-angles of 115° and −72° and RMS deviations of 11° and 12°. Thus, the presence of the dummy atom and the pulling protocol do not affect the glycosidic angle conformation or flexibility.

Multistep MD simulations energetics

The evolution of the van der Waals and electrostatic interaction energies of the protein and the ligand along the path of the unbinding simulations (Fig. 3, top; data for the Gal(β1-4)glcNAc/galectin-1 complex) shows that the van der Waals and electrostatic protein-ligand interaction energies start with negative favorable values (∼−65 and −10 (kcal/mol), respectively), and become more positive until step 4 (after pulling 4 Å) when they start to plateau, indicating that there is no longer a significant interaction between the disaccharide and the protein.

Figure 3.

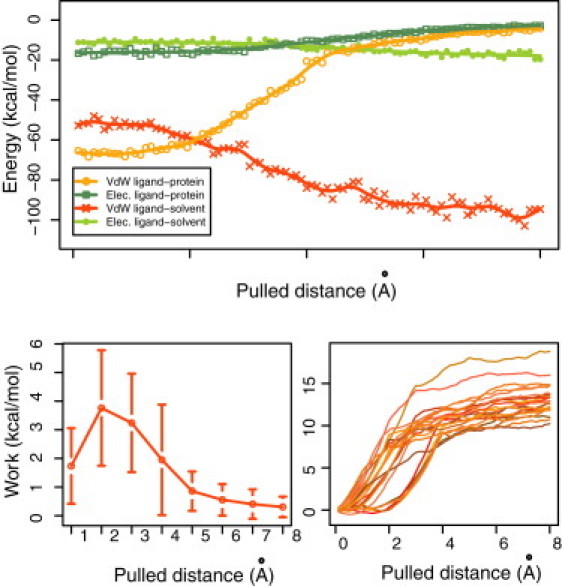
Energetics of binding along the reaction coordinate for unbinding simulations. (Top) Electrostatic and van de Waals interaction energies during a trajectory of an unbinding simulation for the galectin-1/Gal(β1-4)GlcNAc complex (bars represent one standard deviation). (Bottom left) Work done per long-step for different trajectories. (Bottom right) Cumulative work done over different unbinding trajectories.

As expected, ligand-solvent interaction energies show the opposite behavior. As the ligand is pulled away from the binding site and ligand-protein interactions are broken, they are replaced by ligand-solvent interactions. In this case, both electrostatic and van der Waals interaction energies with the solvent increase (become more negative) as the ligand becomes unbound from the binding site. No significant differences in behavior are observed among the eight disaccharides.

For every step, the force and work exerted on the disaccharide were calculated. The total force is the sum of the contributions of each of the three forces of the atoms harmonically restrained to the dummy atom, projected in the direction of the pulling axis. The work of each step averaged over all trajectories of Gal(β1-4)glcNAc (Fig. 3, bottom left) shows that the work needed to pull the ligand from 1 Å away from the initial position to 2 Å away represents the region in the reaction coordinate where most ligand protein interactions are broken and replaced by interactions to solvent. Cumulative work values for all 28 trajectories plateau at ∼4 Å (Fig. 3, bottom right), consistent with the distance at which the protein-ligand interaction energy goes to zero.

Binding free energy calculations

Free energies of unbinding (ΔG_ub^sim) were calculated with the MSTC method (23). Binding free energies (ΔG_b^sim = −ΔG_ub^sim) for the eight disaccharides and for a galactose monosaccharide are presented in Table 1, together with experimental ITC measurements for the same ligands (interpolated to a temperature of 298 K) from the data of Schwarz et al. (14).

Table 1.

Free energy (ΔG) of binding for different galectin-1/disaccharide complexes

	ΔGexp(kcal/mol) (1)	ΔGsim(kcal/mol)
Galβ1,4GlcNAc	−5.66	−5.72
MeO-2Galβ1,4Glc	−5.84	−6.50
Galβ1,3GlcNAc	−5.79	−6.45
Galβ1,4Man	−5.39	−6.10
Galβ1,4Fruc	−5.41	−5.21
Galβ1,4Glc	−5.17	−5.62
Galβ1,3Arp	−5.15	−4.14
Galb1,4Glcβ-OMe	−5.00	−5.20

Free energy differences comparison between experimental ITC measurements (ΔG_exp) and computationally estimated with the MSTC method (ΔG_est).

The computed free energy for the galactose monosaccharide is an important control for the method, and allows the estimation of its sensitivity. Experimental measurements showed that the galactose moiety is necessary for binding to galectin-1 but the presence of at least one additional sugar is essential to increase the affinity (31). Given the low affinity of galactose to galectin-1, no calorimetric free energy is available for galactose binding. The free energy of unbinding computed here is 3.0 kcal/mol, ∼2.5 kcal/mol lower, on average, than for most of the disaccharides consistent with the contributions of both monomers to the binding free energy of the disaccharide.

Computed ΔG_b^sim for different disaccharides are in good agreement with the experimentally measured free energies ΔG_b^exp—within a 0.7 kcal/ mol range (with one exception). This agreement is not a consequence of the small differences among the experimental values. The experimental and simulated free energies are linearly related with a slope of 1.1 (Fig. 4, top panel). Error bars calculated using the bootstrap method (32) show that errors are <0.3 kcal/mol. In contrast, the slope of the line between the experimental enthalpy ΔH and the simulation estimated free energy is only 0.7 (Fig. S4), indicating that simulations captured both the enthalpic and entropic contribution to binding. The difference in slopes (1.1 vs. 0.7) and the high correlation (R² = 0.99 for ΔG_b^sim versus ΔG_b^exp and R² = 0.93 for ΔG_b^sim versus ΔH_b^exp) suggests that the free energies of binding of the disaccharides to galectin-1 involve enthalpy-entropy compensation.

Figure 4.

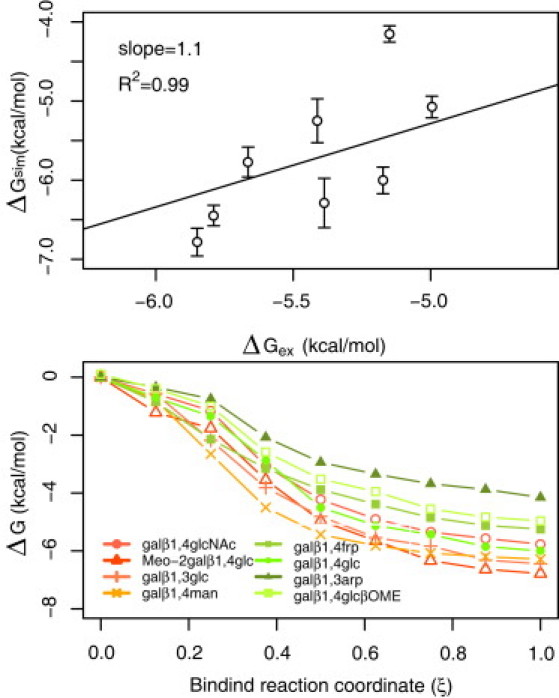
Free energy of binding from unbinding simulations. (Top) Correlation between experimental ΔG_exp and simulations estimated ΔG_sim for all disaccharides. The slope and R² of the linear fit are presented in the plot. (Bottom) Binding free energy profile per step. In the x axis, 0 represents the unbound conformation, and 1 the unbound conformation. Different curves correspond to different disaccharides.

In addition, ΔG_b^sim and ΔG_b^exp rank mainly in the same order for different disaccharides. The largest discrepancy between ΔG_b^sim and ΔG_b^exp is observed for Gal(β1-3)Arp, the disaccharide with the lowest affinity obtained in the computations. The H-bond network of all the disaccharides includes direct interaction of the reducing end sugar unit O3 with residues Arg-48 and Glu-71, where the O3 is in equatorial position. In Gal(β1-3)Arp, the O4 of arabinose is in the axial position, forming H-bonds only with Arg-48. It should be noted that the bound conformations for all disaccharides were modeled, except for Gal(β1-4)GlcNAc. It is possible that the modeled conformation for Gal(β1-3)Arp does not capture the proper set of binding interactions and, as a consequence, underestimates the binding affinity. Another possible source of error in the free energy estimations may be a consequence of the approximate nature of the force-field parameters.

The values of the free energy differences between the bound state and states along the reaction coordinate were computed taking advantage of the multitrajectory characteristic of the MSTC protocol. For this, the free energy of unbinding (ΔG_ub) at each long-step was calculated using Jarzynski's equation. These values (reversed in sign) were used as the cumulative binding free energy as a function of the binding reaction coordinate (zero at 8 Å from the binding site and 1.0 when bound) (Fig. 4). No free energy barriers are observed along the reaction coordinate, suggesting that binding of these disaccharides to the galectin is a diffusion-controlled process. These results reflect the fact that the structure of the binding site is very shallow and no significant conformational change takes place upon disaccharide binding. Because of the absence of large conformational changes, equilibration after each long-step was achieved using fairly short MD runs.

To quantify the improvement in the estimation of ΔG_b obtained using the MSTC method, we compared three estimates of the unbinding free energy: the average work for all 28 unbinding trajectories (〈W_ub〉), the Jarzynski free energy of the 28 trajectories taken as one 8 Å step (ΔG_J), and the MSTC free energy estimate (ΔG_MSTC). In the case of Gal(β1-4)GlcNAc, we obtained 〈W_ub〉 = 12.8 kcal/mol, ΔG_J = 9.8 kcal/mol, and ΔG_MSTC = 5.7 kcal/mol. For all disaccharides, the average ΔG_J − ΔG_MSTC is 4.9 kcal/mol. This difference provides an estimate of the improvement in the estimation of ΔG the results from an improved sampling of the work probability distribution afforded by the MSTC method.

During the unbinding simulations, the dummy atom attached to the disaccharide is always a fixed point. As already discussed, the conformational flexibility of both the protein and the ligand is not affected by the presence of the dummy atom or the simulation protocol. Having the fixed dummy atom restricts the translational degrees of freedom of the ligand and constitutes an unfavorable contribution to the free energy of binding, given the entropy loss. Several ad hoc corrections have been developed to estimate the translational entropy (see for example (33–37)). For a solute, the translational movement depends mostly on the interactions of the molecule with its neighbors. For carbohydrates, the high density of hydroxyl groups results in an extensive H-bond network with the water molecules, which hampers the translation of the solute by requiring a coordinated movement of different groups of the carbohydrate. Thus, in this case, the additional restriction introduced by the tether should result in a minimal effect.

Disaccharide recognition and the role of solvent in the unbinding process

The stereochemical properties of the disaccharides that dictate their interaction with proteins include the nonpolar surface formed by aliphatic CH groups regions and the high density of hydroxyl groups. The aliphatic groups in this surface stabilize binding by participating in nonpolar contacts, including ring-stacking (CH-π) against aromatic residues of the protein (38). Conserved sequences in galectins include aromatic residues as part of the CRD. Mutations of these aromatic residues have significant effect on the binding affinity (39,40). The CRD of galectin-1 has a conserved tryptophan residue. Computational studies (41) showed a significant decrease in the interaction energy when the Trp residue is replaced by Ala. In addition, almost all H-bonds are less stable in the mutant, suggesting that the H-bond network is not sufficient to maintain the disaccharide in the binding site and that stacking interactions are necessary (41).

To evaluate the persistence of this interaction, we calculated for the galectin-1/Gal(β1-4)GlcNAc complex the angle between the normal to a least-square plane adjusted to the galactose ring and the normal to the ring of the Trp-68 residue (Fig. 5). During the initial equilibration, the angle between the plane normals is 47 ± 17°, comparable to the crystallographic angle of 50°. This stacking conformation is preserved during the initial equilibrations, the first long-step and a fraction of the second long-step. For all trajectories, a conformational change occurs at ∼1.5 Å from the initial bound conformation, with change in the angle of ∼30°. In most cases, the angle between the plane normals increases; the space between the rings opens first on one side, allowing solvent molecules to enter the interface. This result agrees with previous studies where, using Raman spectroscopy and MD simulations, Di Lella et al. (21) showed that, upon ligand binding, no major conformational change takes place, but substantial solvent reorganization occurs in the proximity of Trp-68.

Figure 5.

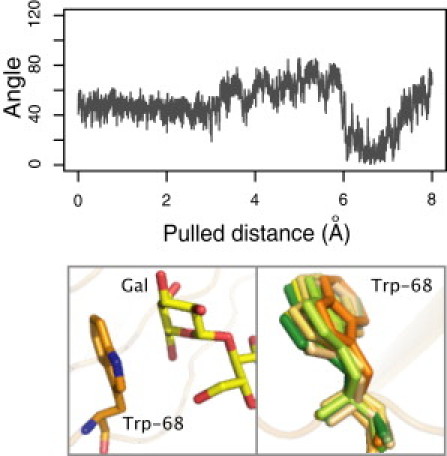
Trp-68 stacking conformation during the unbinding simulations. (Top) Angle between the normal to a least-squares plane adjusted to the galactose ring and the normal to the ring of the Trp-68 residue during one unbinding trajectory of the galectin-1/Gal(β1-4)GlcNAc complex. (Bottom left) Initial stacking conformation between the galactose unit and Trp-68. (Bottom right) Overlap of different Trp-68 conformations during the unbinding simulation. (Orange tones) Initial structures; (yellow) intermediate structures; and (green) final structures.

The specificity and affinity of galectin-1 for different β-galactosides are in part determined by H-bonds formed between the carbohydrate hydroxyl groups and different residues in the protein, resulting in an intricate cooperative H-bond network. The initial H-bond network for every galectin-1/disaccharide complex was characterized. Table S1 (Supporting Material) shows the occupancies of different H-bonds during the initial equilibration of the system. In a previous study, Schwarz et al. (14) showed that there is no correlation between the binding enthalpy and the number of H-bonds formed in the bound conformations.

This observation is consistent with results obtained by MD in this work. Table S1 also shows that the galactose units of all the disaccharides present the same H-bond pattern and similar occupancies, except for Gal(β1-3) Arp, for which some occupancies are lower. For the nonreducing end sugar unit, the H-bond network and the relative occupancies vary among different disaccharides, but the average occupancies are comparable. Comparison of the initial configurations shows no particular structural differences that can be identified as determinants of a higher or lower binding affinity. In the case of Gal(β1-3)Arp, the lower number of H-bonds and occupancies in the initial conformation are compensated by water-bridged H-bonds (data not shown). This behavior is common in other carbohydrate-lectins complexes, in which different side-chain rotamers mediate interactions either by direct or water-mediated H-bonds to give rise to a locked conformation (42).

From the galectin-1 perspective, breakage of H-bonds can be quantified as a function of the pulled distance by evaluating two parameters:

• 1.The number of disaccharide-protein H-bonds present at each step.
• 2.The fraction of the time each of the CRD's donors/acceptors makes an H-bond to the disaccharide.

This analysis shows that each complex has a different initial set of H-bonds and each evolves differently as the ligand is pulled from the binding site (Fig. 6). For all disaccharides, as they are pulled from the binding site, direct and bridged H-bonds are formed with residue Trp-68 that were not present in the bound conformation. These observations suggest that Trp-68 not only plays a role in positioning the galactose ring in the binding site, but also in the initial recognition of the sugar during binding (the reversal of the process computed in the pulling simulations). A similar behavior is observed for disaccharides with β1-4 glycosidic bonds, which, as they become unbound, form contacts with His-52. If the overall occupancy of H-bonds during unbinding is considered, Gal(β1-4)GlcNAc has the highest occupancy of both direct and bridged H-bonds. In contrast, Gal(β1-3)Arp has the lowest occupancy of direct H-bonds, but has an ∼40% higher frequency of water-bridged H-bond occupancy compared with the other disaccharides.

Figure 6.

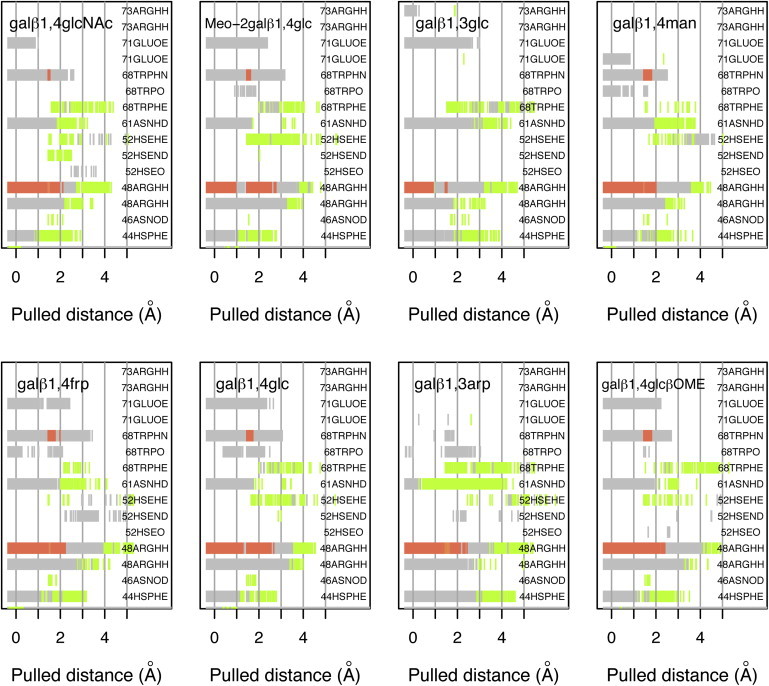
H-bonds for different galectin-1/disaccharide complexes along the reaction coordinate. H-bond network between galectin-1 and the different ligands as a function of the pulled distance. (Gray) 1 H-bond; (red) >1 H-bond; and (green) H-bond bridged by a water molecule.

As disaccharides become unbound from the binding site, H-bonds can be broken by two different mechanisms (Fig. 6). The first mechanism involves direct elongation and breakage of the bond; in the second mechanism, the bond is elongated while a water molecule makes H-bonds with both the donor and the acceptor. In Fig. 7, the distance between the galactose O6 of the disaccharide Gal(β1-4)GlcNAc and the nitrogen from Asn-61 is plotted for a single trajectory. The H-bond is broken in a stepwise manner by bridging the interaction first by one water molecule and later by two water molecules. Note that, when two water molecules are bridging the protein-disaccharide interaction, it involves the galactose O4 (not O6), yet still restrains the distance. This stepwise distance elongation between donor acceptor pairs is observed in all H-bonds that break by water bridging. The shallow binding site makes it possible for water molecules to access the binding interface and exchange protein-ligand H-bonds to protein-water-ligand H-bonds whenever the first H-bond becomes elongated (i.e., destabilized with respect to the H-bonds to water).

Figure 7.

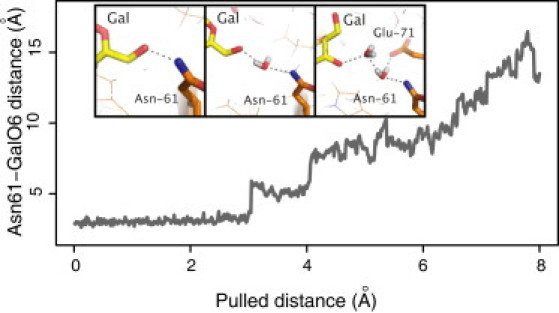
Water molecule H-bond bridging: Donor-acceptor distance of the galactose-O6·Asn-61 H-bond during one unbinding trajectory. A stepwise elongation is observed. Snapshots represent structures at distances where a water molecule is bridging the interaction between the protein and the disaccharide.

Summary and Conclusions

The interaction between galectin-1 and eight β-galactosamide-derived disaccharides was studied using MD simulations. Binding free energies were estimated using a multistep trajectory combination (MSTC) method developed by us and used previously to estimate helix propensities (23). This is the first time, to our knowledge, that the MSTC method has been used to calculate binding free energies and the results of the calculations show that the procedure is a powerful and robust tool. Calculated binding free energies show excellent agreement with experimental ITC measurements and the method is sensitive enough to discriminate among different disaccharides.

The simulations provide mechanistic insight into the thermodynamic and structural basis of disaccharide recognition by galectin-1. Analysis of the cumulative free energy of unbinding along the reaction coordinate shows that no energy barriers need to be crossed (Fig. 4), suggesting that binding is diffusion limited. This observation is further validated by the fact that no major conformational changes are observed upon unbinding. In particular, Trp-68, which participates in a stacking interaction with the galactose ring and is necessary to position the sugar in the binding site, only experiences a small side-chain conformational change as the ligand unbinds, allowing water molecules to reorganize in the interface. In addition, simulations suggested that His-52 and Trp-68 are necessary for sugar recognition before binding.

Analysis of the structures along the reaction coordinate, in particular with regard to H-bond formation and occupancies, revealed additional details about the mechanism of disaccharide binding to galectin-1. In the initial structures and the initial equilibrations, H-bond formation and occupancies are comparable among the eight complexes, and compensation between direct and water-bridged H-bond is observed (Fig. 6). The mechanism of unbinding is best described in terms of H-bond weakening by elongation as water molecules bridge the donor-acceptor atoms, resulting in a stepwise separation of the donor-acceptor pairs. This observation agrees with previous studies showing that solvent reorganization plays an important role in the carbohydrate-binding process (16,19,43).

Galectin-1 binds different β-galactosamides with similar affinities because of a combination of different factors including the use of direct or water-bridged H-bonds, depending on the configuration of the hydroxyl groups. This ligand promiscuity allows galectin-1 to recognize N-acetylglucosamine units of N- and O-linked sugars on the surface of immune and tumor cells and facilitate phenomena such as cell migration, cell adhesion, and immunosuppression. In addition, this ligand promiscuity will place restrictions on the design of inhibitors for galectin-1. Detailed knowledge of the structure and the binding energetics of the complexes such as the ones presented here is key to designing novel glycomimetics for therapeutic interventions. For example, our results suggest that the galectin-1 inhibitor should balance ligand-protein and ligand-solvent interactions in a way that achieves high affinity and specificity.

In this article, the agreement of the calculated free energies with the experimental data validates the procedures used and provides strong support for the observations of the mechanistic details underlying molecular association. Computation of free energies of binding such as those presented here can provide new insight into two different and complementary situations. They can be used to obtain estimates of the binding free energies when experimental data are not available. When experimental data are available, the computed values of the free energy can be compared to the experimental values to validate the computations. If the computed values prove to be accurate, analysis of the trajectories provides mechanistic insight about the details of binding and unbinding.