Abstract
In spite of the advantages associated with the molecular specificity of fluorescence imaging, there is still a significant need to augment these approaches with label-free imaging. Therefore, we have implemented a form of interference microscopy based upon phase-shifted, laser-feedback interferometry and developed an algorithm that can be used to separate the contribution of the elastically scattered light by sub-cellular structures from the reflection at the coverslip-buffer interface. The method offers an opportunity to probe protein aggregation, index of refraction variations and structure. We measure the topography and reflection from calibration spheres and from stress fibers and adhesions in both fixed and motile cells. Unlike the data acquired with reflection interference contrast microscopy, where the reflection from adhesions can appear dark, our approach demonstrates that these regions have high reflectivity. The data acquired from fixed and live cells show the presence of a dense actin layer located ≈ 100 nm above the coverslip interface. Finally, the measured dynamics of filopodia and the lamella in a live cell supports retrograde flow as the dominate mechanism responsible for filopodia retraction.
OCIS codes: (180.3170) Interference microscopy, (170.1530) Cell analysis
1. Introduction
Since its inception to measure the adhesion of cells to a transparent substratum, [1–3], interference reflection microscopy (IRM) and reflection interference contrast microscopy (RICM) have yielded significant insights about the location and size of adhesion complexes and “focal contacts” (a name coined from an early application [4]). Although RICM can yield quantitative results when applied to imaging spheres [5] and vesicle adhesion [6,7], the method, which is applicable to live cell imaging [8], has unfortunately not realized the potential for high precision measurements when applied to cells. One significant impediment is that analysis of the intensity variations in a set of interference fringes can lead to ambiguities because it is difficult to separate changes in topography from local variations in protein concentration near the ventral plasma membrane [9, 10]. Alternatively, the application of fluorescence interference contrast microscopy [9, 11, 12] has demonstrated that it is possible to use specific fluorescent labeling to quantitatively probe the dynamics of membranes and the position of the ventral plasma membrane with nanometer precision. Indeed the molecular specificity of fluorescence based methods have enabled the imaging of the morphology of adhesions with resolution below the diffraction limit [13–15]. In spite of the advantages associated with fluorescent imaging, there is still a need to augment these approaches with label-free, interference imaging that can probe protein aggregation, index of refraction variations and structure [16, 17].
An approach based upon phase-shifting interferometry would mitigate these inherent limitations, but the potential impediments have appeared daunting because of the low reflectivity and complexity associated with elastic light scattering from sub-cellular features. Recent work, however, has demonstrated the power of using elastic light scattering methods [18] to probe actin dynamics [19, 20], cell structure [21, 22] and surface membrane waves [23, 24] in live cells.
In this paper, we present a form of reflective confocal interference microscopy [25] based upon laser-feedback interferometry [26–30] combined with phase-shifting techniques which yields the phase and amplitude of the reflected field [29–31]. After presenting the basis of the method, we apply the technique to measure integrin adhesions in both a fixed and a motile cell. Although the morphology of these adhesions has been characterized, the mechanisms that govern the formation and lifetime of these adhesions remains a hot topic of research [32, 33].
In order to relate the phase and amplitude of the reflected field that we measure to the topography and reflectivity of cellular features near the ventral plasma membrane, we have developed an algorithm that can be used to separate the contribution of the elastically scattered light by sub-cellular structures (or a calibration sphere) from the reflection at the coverslip-buffer interface. In essence, we solve this inverse problem [34] so that we can find the local topography and reflectivity of the sample from a set of interference measurements. We also address the forward problem such that, given a priori information about the shape and index of refraction (e.g. of a calibration sphere), we can predict the experimentally observed phase and reflectivity [35, 36].
Although we are predominately interested in the solution to the inverse problem because the majority of applications lack a priori information regarding the object’s reflectivity and shape, the solution to the forward problem is useful for interpreting data for calibration. As an application of the forward problem, the results of two closely related experiments are analyzed: (1) linear translation of a planar coverslip-buffer interface away from the focal plane of a microscope objective and (2) reflection from the surface of a polystyrene sphere < 100 nm above the coverslip-buffer interface. These two experiments provide a calibration of the profile of the focused light from the objective and they lay the foundation for a comparison with results of our inverse method.
Subsequently, we demonstrate that the inverse method as applied to phase data collected from the sphere is consistent with the solution of the forward problem. Finally, we apply our inverse method to phase data acquired from light that was reflected from stress fibers and focal adhesions on the ventral plasma membrane, which lies in apposition to the coverslip-buffer interface. In contrast to the application of RICM, where a high concentration of protein in focal adhesions may appear black [37], phase-shifted laser feedback interferometry combined with our solution of the relevant inverse problem clearly demonstrate that these regions provide a strong, bright signal indicating that they have higher reflectivity than the surrounding areas.
2. Methods
2.1. Instrument
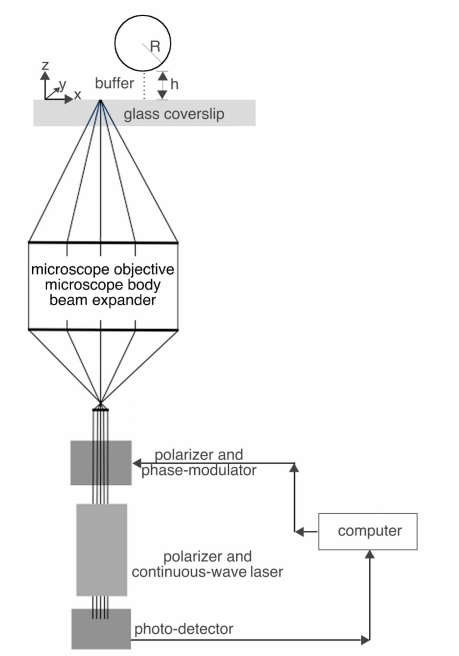
As illustrated in the schematic in Fig. 1, the scanning laser feedback interference microscope consists of a custom-designed interferometer coupled to an inverted microscope (TE2000U, Nikon). The interferometer is based upon a low power, continuous-wave (CW) helium-neon laser (1107P, Uniphase) whose output light passes through a linear polarizer (5524, New Focus) and a broadband electro-optic phase-modulator (4002, New Focus); the polarization is aligned such that only pure phase modulation is achieved. After passage through a subsequent linear polarizer, the laser beam is expanded with a beam expander so that the TEM00 mode slightly under-fills the back aperture of a microscope objective (CFI60 100x, NA =1.45 or a 60x, NA =1.3, Nikon). The light enters the microscope via the left-side port and illuminates the sample without passing through a tube-lens, a dichroic mirror or a filter. The modulated intensity of the laser is monitored with a photodetector (1201, New Focus) that collects the small percentage of light that is transmitted through the back laser mirror; the voltage from the detector was sampled using an analog-to-digital convertor (DAS1802, Keithley).
Fig. 1.
Schematic diagram of experimental configuration of the laser feedback interference microscope. Linearly polarized light from a low power continuous-wave helium-neon laser passes through a broadband electro-optic phase-modulator and is subsequently expanded so that the TEM00 mode fills the back aperture of a high numerical microscope objective. The modulated intensity due to laser feedback of light from the sample is monitored with a photodetector at the back mirror. A single computer controls the phase shifts to the modulator, reads the photodetector signal and controls the piezoelectric stage that moves the sample.
In order to implement the phase shifting algorithms, five discrete voltages were sequentially superimposed upon the modulator using an analog-to-digital convertor (DAS1802, Keithley) and high-voltage function generator (3211, New Focus). In order to build up an image from a series of discrete measurements, the sample was translated using a closed-loop piezoelectric stage that can move independently along three orthogonal axes (LP100, Mad City Labs); x,y are in the transverse plane and z is along the optical or axial axis. Both the spacing between pixels (pixel step size) and the direction of the scan were variable. For the axial scans (Section 4.1), the step-size along the optical (“z” axis) was set to 20 nm; ten scans were acquired and averaged. When imaging either an interface or spheres, the step-size along either of the two transverse axes was set to 100 nm between pixels. When imaging cells, we used a small step-size of 50 nm between pixels. The pixel dwell time, which includes the time to acquire the raw data with on-the-fly presentation of the raw phase and visibility to the computer monitor is ≈ 0.01 seconds; this does not include the post-processing time to implement the algorithms. Therefore, the 400 pixel x 600 pixel image covering 20μm x 30μm in Figs. 6(C) and 6(D) with 50 nm/pixel, required approximately 40 minutes to acquire.
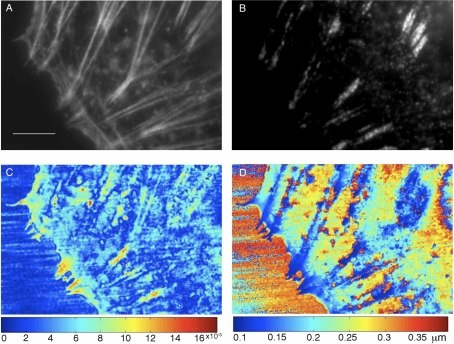
Fig. 6.
Fluorescence and interference images obtained near the ventral plasma membrane of fixed cells. (A) Immunofluorescence image showing F-actin localization near the periphery of the cell. (scale bar: 5μm). (B) Immunofluorescence image of the density of paxillin. (C) Fringe visibility and (D) height of the reflective features above the coverslip-buffer interface at discrete scan points that cover the same region as the fluorescence images calculated using the inverse method (Eqs. (8) and (9)). The height, z, was determined from the phase, θ, as: with λ = 0.6328 μm, nb = 1.333 and f = 1.2. Using this method, the height map represents the distance above the coverslip.
All samples (in 35 mm microwell glass-bottom dishes (MatTek Corporation)) were held in a custom designed tip-tilt insert that fit into the piezoelectric stage. In order to correlate the pixels in the interference image with those pixels in the fluorescence image collected with a CCD (Coolsnap, Princeton Instruments), a single affine transformation (consisting of a scaling and a rotation) was applied to the scan region and the edges of the transformed images were subsequently cropped by a few pixels to produce rectangular regions. Custom written software (Labview, National Instruments) was used to control the equipment. Data analysis was performed with either Matlab (Mathworks) or Mathematica (Wolfram Research).
2.2. Assays
We imaged the coverslip-buffer interface above an unmodified #1.5 coverglass of 35 mm microwell glass bottom dishes (MatTek Corporation) filled with α-MEM media (Invitrogen). We used immersion oil (Cargille type DF; Cargille Laboratories) between the objective and the glass coverslip. Based upon data supplied by the manufacturer, we calculated the index of refraction at the imaging wavelength (λ = 0.6328μm) to be n = 1.515. We performed calibration experiments using polystyrene spheres that had 15μm nominal diameter (FocalCheck, Molecular Probes). These spheres were placed in a 35 mm microwell plate that contained water and a Poly-L-lysine coated (P8920, Sigma, diluted to 0.01%) coverslip. The majority of spheres settled at a small unknown distance, ho above the coverslip such that Brownian motion was essentially undetectable. From the Cauchy dispersion relation, we determined the index of refraction for the polystyrene sphere at the imaging wavelength (λ = 0.6328μm) to be n = 1.582 [38].
2.3. Cell Culture
We imaged both fixed and live non-metastatic rat mammary adenocarcinoma MTC cells. Cells were cultured in α-MEM media supplemented with 5% FBS and pen/strep (Invitrogen) [39,40]. Cells were trypsinized and plated onto the microwell dishes 24 hours prior to fixation and staining. The cells were starved for one hour using bovine serum albumin and then stimulated by epidermal growth factor for one minute. Finally, cells were rinsed two times with PBS and fixed with 4% paraformaldehyde diluted in PBS before being permeabilized with 0.1% triton X-100/PBS for 10 minutes. Focal adhesions were identified using indirect immunofluorescence with a primary antibody against paxillin (clone 349) (BD Biosciences) and a goat-anti-mouse IgG secondary antibody conjugated with Alexa Fluor 488 (Invitrogen). F-actin was stained using rhodamine-phalloidin. These probes were easily excited and spectrally separated using readily available filter cubes (e.g. FITC and TRITC).
2.4. Phase Shifting Interferometry
The basis of phase shifting interferometry is to use an over-determined set of independent intensity measurements, so that it is possible to solve for V and Φ and to eliminate the variable Io in Eq. (1):
| (1) |
We employed a popular algorithm that uses five discrete phase shifts in order to reduce the sensitivity to random errors in the phase shift, [41]: ψi = {–π, , 0, , π}. The visibility and phase can then be determined from the measured intensities using Eqs. (2) and (3):
| (2) |
and
| (3) |
The phase, Φ, in Eq. (3) is determined from the inverse tangent function such that . In order to map the phase to a range 0 ≤ Φ ≤ 2π, the sign of the numerator and denominator in Eq. (3) are examined separately and a factor of π is either added or subtracted to the phase [42, 43]; the closely related, two argument function “atan2” defined between −π ≤ Φ ≤ π automatically accounts for the quadrant for the phase and accomplishes the same result. Because the phase is determined modulo 2π, visible 2π discontinuities between pixels may occur which may be removed using unwrapping algorithms that, depending upon the sign of the phase discontinuity between adjacent pixels, either add or subtract an integer multiple of 2π.
3. Modeling the Visibility and Optical Path Length
As indicated in Section 2.1, the basis of our phase-shifted laser feedback interference (LFI) imaging is an inverted microscope where sample illumination is provided by a low-power, continuous-wave, linearly polarized laser. Using a piezoelectric stage that translates the sample, we produce an image by collecting data line-by-line in a two-dimensional raster format with a scan line that begins in a “sample-free” region that contains only buffer above the coverslip and proceeds pixel-by-pixel into a “sample” region that contains either cells or a calibration sphere. At the end of the scan-line, the scan position is returned to the “sample-free” region and is incremented along the orthogonal direction. Unless we specifically want to characterize the effect of defocus, the coverslip-buffer interface is held fixed at the focus of the objective and an axial scan is not performed.
Using phase-shifted LFI microscopy (psLFIM), the steady-state change in the intensity of the laser caused by weak feedback of elastically scattered light may be written in a form that is commonly used to represent the interference of two coherent waves [27, 29]: Ii(x⃗) = Io(x⃗){1 +V(x⃗)cos(Φ(x⃗) +ψi)} where Io(x⃗), V(x⃗) and Φ(x⃗) represent: a background intensity; the Michelson fringe visibility and the optical phase difference between the two fields, respectively. After introducing a discrete, experimentally controlled phase shift, ψi, the corresponding intensity measurement, Ii, is measured (henceforth, we will suppress the notation that represents the spatial variation of the parameters). The phase shifting algorithm can be applied to the measured intensities, Ii, in order to determine the visibility and phase independently of one another and independently of the background intensity, Io.
In LFI, the fringe visibility, V, is proportional to the electric field that is reflected by the sample; because the coupling efficiency of the laser feedback interferometer is less than 100%, the fringe visibility is always less than the maximal value that would be calculated purely on the basis of the Fresnel reflection coefficients (previous work indicates a coupling efficiency of about 40% [27–29]). Because the fringe visibility is intimately related to the reflection coefficient, we will now use the terms “fringe visibility” and “reflectivity” interchangeably.
As with other forms of interferometry, the change in optical phase is related to the optical path length, OPL, between the points p1 and p2, as: [44]. Near the focal plane of a high numerical aperture objective, however, the phase changes nonlinearly with defocus [45, 47, 48] and accumulates a phase shift of for positive defocus. When the sample is imaged close to the focal plane, the effect of the nonuniform spacing of the interference fringes may be approximated with a constant factor, f (> 1), so that the optical path length is related to the phase as: [45, 47].
Regardless of the location of the scan position, we can interpret the measurement as containing a contribution from “signal” and “background”. In the “sample-free” region, the reflected light that re-enters the laser consists of a reflection from the coverslip-buffer interface (“signal term”) and a considerably weaker reflection from the optical elements along the path (“background term”); because of the index-matching oil, the reflection from the bottom of the coverslip is negligible. These two reflected fields give rise to an observable interference signal. After translating the scan position to the “sample” region, we interpret the “signal term” as consisting of light reflected from the sample (cell or calibration sphere) which interferes with the “background term” that arises from the field reflected from the coverslip-buffer interface and the reflections from the optical elements.
In either the “sample-free” or “sample” region, we model the interference from the multiple reflections as arising from two discrete fields that interfere inside the laser cavity. These multiple reflections may be modeled as a change in the effective reflectivity of the laser mirror such that the measured intensity may be written as Eq. (4) [26, 28, 29]:
| (4) |
In the “sample-free” region, the parameters {A, ϕ} in Eq. (4) represent the visibility and accumulated phase associated with the weak reflections from the optics along the path (“background term”) and the parameters {B, θ} represent the subsequent reflection that occurs after the partially transmitted field is reflected from the coverslip-buffer interface (“signal term”). By contrast, when the scan position has been translated into the “sample” region, the visibility A represents a “background term” which consists of the reflection from the coverslip-buffer interface (and the weaker reflection from the optical elements) and B represents the “signal term” that arises from light that is reflected from the sample. Accordingly, in either region, ϕ and θ represent the phases that have accumulated following the reflection from the primary interface (optical elements or coverslip-buffer) and the secondary interface (coverslip-buffer or sample), respectively.
A little algebra allows Eq. (4) to be represented as Eq. (5) which is then amenable to the application of the phase-shifting algorithm:
| (5) |
where the visibility, m, and phase, γ, are related to the variables in Eq. (4) as:
| (6) |
and
| (7) |
In the “sample-free” region, determining the parameters {B, θ} associated with the reflection from the coverslip-buffer interface is primarily relevant. Once the scan position has been translated to the “sample” region, however, we wish to determine the parameters {B, θ} which are associated with the reflection from the sample.
3.1. Predicting the Visibility and Optical Path Length Using A Priori Information: the Forward Problem
We formulate the forward problem: given estimates of the fringe visibility and phase {A, ϕ} and {B, θ}, predict the measured values m and γ. Using Eqs. (6) and (7) and a priori information so as to estimate {A, ϕ} and {B, θ}, we make an initial prediction of the visibility and phase, m and γ, and refine the estimate after comparison with the measured values.
3.2. Determining the Topography and Index of Refraction of a Sample Without A Priori Information: the Inverse Problem
As an alternative to the forward problem, it is possible to formulate the inverse problem: given measurements of the visibility and phase {m, γ}, find the unknowns {B, θ} associated with the reflection from the sample. The approach to the inverse problem as applied to reflections from multiple interfaces begins with a direct solution of Eqs. (4) and (5) for the reflectivity, B, and phase, θ:
| (8) |
and
| (9) |
Therefore, provided that the values {A, ϕ} have been measured, Eqs. (8) and (9) may be combined with a measurement of {m, γ} in order to determine the value of the visibility and phase, {B, θ}, associated with the reflection from the sample.
4. Results
4.1. Application of the Forward Problem: Change in the Visibility and Optical Path Length Following Defocus of the Coverslip-Buffer Interface
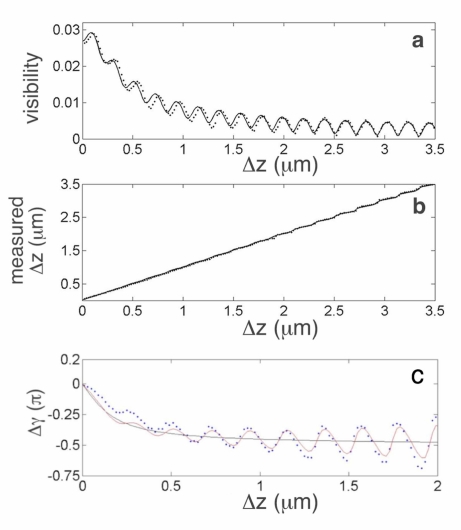
Figure 2(a) and 2(b) (dotted lines) shows the visibility, m, and measured position of the interface, Δzm (obtained from with λ = 0.6328μm and n = 1.515) measured in the “sample-free” region as a function of the imposed displacement, Δz, of the coverslip-buffer interface. The data in Fig. 2(a) show that as the defocus increases, the visibility oscillates with a superposed decay envelope. The measured stage position, Fig. 2(b), appears to increase linearly and there are superposed weak oscillations that become increasingly pronounced with defocus. Although a departure from linear phase variation with a small amount of defocus is not readily evident in Fig. 2(b), this effect is clearly observed after a line with slope 4πn/λ is subtracted from the data. Fig. 2(c) (dotted lines) shows Δγ = γ – (4πn/λ)Δz as the coverslip-buffer interface was translated away from focus by Δz = 2μm.
Fig. 2.
Effect of defocus on visibility of the interference fringes from a coverslip-buffer interface. (a) Change in the measured visibility, m, (dotted lines) as the coverslip-buffer interface was translated by Δz; solid line is based upon a solution to the forward problem (Eq. (6)). (b) Position of the interface, Δzm = λγ/(4πn), as a function of defocus (dotted); solid line is based upon Eq. (7). (c) Difference between measured and predicted phase, Δγ = γ – (4πn/λ)Δz, near focus (dotted). Plot of ΔγG = – tan−1(2Δz/zo) (solid black line) where zo = 0.3μm. Predicted variation (solid red line) on the basis of Eq. (7) with θ = (4πn/λ)Δz – tan−1(2Δz/zo) + π.
In order to predict the observed visibility and phase data using Eqs. (6) and (7), we need initial estimates for A, B and θ; without loss of generality, the overall phase factor, ϕ, may set to zero. Initially, we estimate the maximum reflection from the interface as B = κ|r|, where κ = 44% is the expected coupling efficiency and r is the Fresnel coefficient at normal incidence; using the index of refraction for glass and buffer as 1.515 and 1.333, respectively, we have B ≈ 0.44×0.064 ≈ 0.028. It is more challenging to determine an initial estimate for A, however, if we assume that 2% of the incident field is reflected from the optical elements (i.e. a reflection that is consistent with the anti-reflecting coating at the back of the objective), then we can estimate A ≈ 0.44 × 0.02 × 0.20 ≈ 0.0018.
We model the observed envelope of the visibility in Fig. 2(a) by assuming that the reflection from the coverslip-buffer interface falls off with defocus as the square-root of a Lorentzian function; this functional form is a good approximation to the axial profile of the electric field of our Gaussian-Lorentzian TEM00 laser beam focused by the microscope objective [45, 46]. Therefore, we have where is the half-width at half-maximum, Bo = 0.028, σ ≈ 0.3μm for our microscope objective [45] and Δz is measured in microns.
The linear phase change in Fig. 2(b) is proportional to the imposed linear translation, Δz, of the coverslip-buffer interface as θ = (2π/λ)n2Δz where n = 1.515 and λ = 0.6328μm. Therefore, the analysis of the forward problem may be used to predict the measured visibility and the change in phase using Eqs. (6) and (7), respectively. Figures 2(a) and 2(b) (solid lines) show the result of a non-linear least squares fit with parameters A, B and σ (with initial estimates of A =0.0018, B = 0.028 and σ = 0.3, respectively) such that A = 0.0019 and with θ = 30.00 radμm−1 Δz.
Theory predicts that the observed phase also depends upon the numerical aperture of the microscope objective [45]. Because of the nonlinear variation with defocus (Fig. 2(c)) there is an accumulated phase difference –π/2 at large defocus which is known as the Gouy phase shift [48]. Figure 2(c) (solid black line) shows this predicted phase anomaly, ΔγG = –tan−1(2Δz/zo), where zo = 0.3μm. Therefore, it is appropriate to refine our predicted linear phase variation, θ = (4πn/λ)Δz, by including a nonlinear term −tan−1(2Δz/zo). Figure 2(c) (solid red line) shows Δγ based upon Eq. (7) using θ = (4πn/λ)Δz − tan−1(2Δz/zo) + π and the parameters that resulted from the fit to the data in Fig. 2(b) (i.e. A = 0.0019; ; n = 1.515 and λ = 0.6328μm). Following convention, we express the variation of phase near the focal plane for small values of defocus as θ ≈ (4πn/λ) f−1Δz where f−1 is a constant factor [47]. Using a linear expansion of tan−1(2Δz/zo), we obtain f−1 ≈ 0.8. Conversely, given a phase measurement near focus, θ, the interface is at height above the focal plane, where f = 1.2.
4.2. Application of the Forward Problem: Reconstruction of the Visibility and Optical Path Length to the Surface of a Sphere at a Small Distance from the Coverslip-Buffer Interface
In a second closely related demonstration of the application of the forward problem, we imaged polystyrene spheres and measured the interference between light reflected from the sphere and light reflected from the coverslip-buffer interface. This relatively large sphere was imaged with the focus of the objective held fixed at the coverslip-buffer interface; this approach assured that the reflection from the (bottom) surface of the sphere closest to the coverslip-buffer interface was greater than the (top) reflection from the surface of the sphere that was furthest from the interface.
By analogy with the analysis of the planar interface, we address the forward problem: given the fringe visibility and phase associated with the reflection from the coverslip-buffer interface {A, ϕ} and the sphere {B, θ}, find m and γ on the basis of Eqs. (6) and (7). From the initial experiment with a planar interface, we are able to estimate the reflectivity, A, from the value of the fringe visibility when the interface is in focus, i.e. Δz = 0 in Fig. 4(a), as A = 0.035. In addition to representing the dominant reflection from the coverslip-buffer interface, the term A also accounts for the constant, considerably weaker reflections from the optical elements.
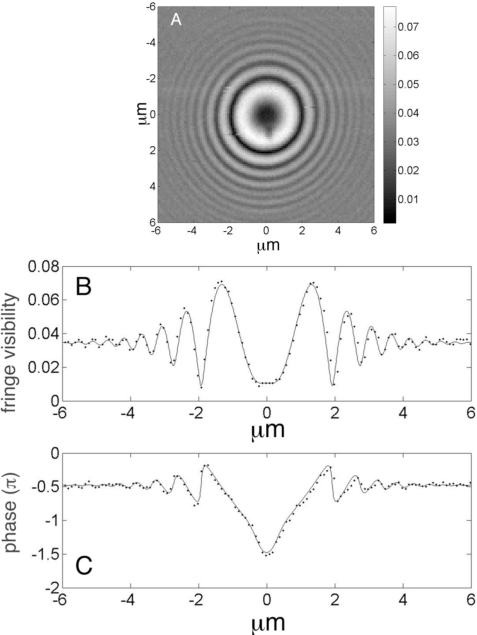
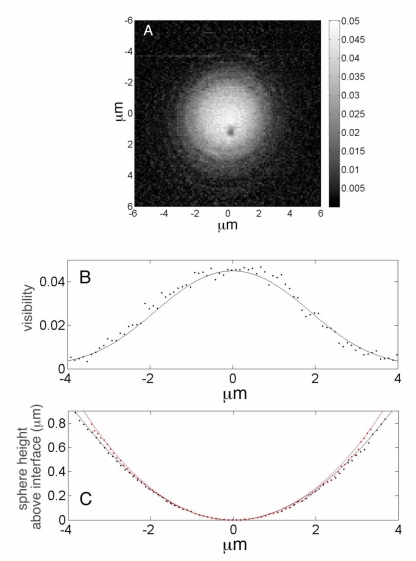
Fig. 4.
(A) Visibility of the fringes from the surface of a 7.7μm radius polystyrene sphere in water. (B) Fringe visibility and (C) phase from a single row of pixels; the analytical fits (solid lines) are based upon analysis of the forward problem and dotted lines are experiment.
When imaging the reflection from a tilt-free, planar reflector at the focus of a high numerical microscope objective, all of the incident rays will be collected by the objective, however, for a sphere the angle of reflection of an incident ray at the sphere’s surface depends upon the transverse scan position. Therefore, unlike the reflection from the planar interface, the angle of reflection of an incident ray at the sphere’s surface depends upon the transverse scan position and the visibility, B, and OPL depend upon the angle of incidence. Because we do not have an analytical description for the bidirectional reflectance distribution function (BRDF) that describes the reflection from the sphere [49], we approach the fit to the data by invoking a “tangent-plane approximation” which assumes that light is reflected from a diffraction-limited patch on a local tangent plane at the sphere’s surface [50]. Therefore, when the scan position is directly beneath the center of the sphere, light is reflected from a tangent plane that is parallel to the plane of the coverslip-buffer interface, and consequently the optical path will be parallel to the optical (z) axis.
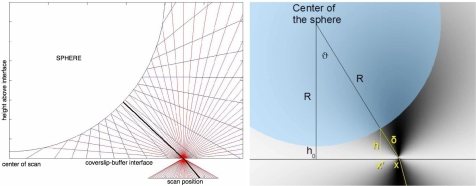
As shown in Fig. 3, when the scan position is not at the center of the sphere, the majority of incident rays that reflect from the sphere’s surface (blue lines) are reflected at an angle such that they do not re-enter the objective (red lines). Instead, only those rays that are reflected from a diffraction-limited patch on a local tangent plane at the sphere’s surface (shown in black) are collected by the objective. Therefore, as the scan position moves outward from the center of the sphere, the optical path can be determined by tracing the path of the ray between the focus and the point where the tangent plane intersects the sphere [51]. Therefore the retro-reflected ray follows a path which forms an angle, ϑ, with respect to the optical axis.
Fig. 3.
Imaging geometry when scanning a sphere. When the scan position is directly beneath the center of the sphere, light is reflected from a tangent plane that is parallel to the plane of the coverslip-buffer interface, consequently the optical path will be parallel to the optical (z) axis. As the scan position moves outward from the center of the sphere, the optical path can be determined by tracing the path of the ray from the microscope objective that intersects the sphere normal to the tangent plane and reflects back into the objective. Therefore, the optical path, δ = OPL/(2n), at the scan position, x and the perpendicular distance, h, from the interface (at x′) to the tangent plane.
We define the center of the scan as the unique position where light is reflected from a tangent plane that contains the coverslip-buffer interface such that the optical path will be parallel to the optical (z) axis (Fig. 3). At this location, OPL = n2ho where ho is the height of the sphere above the coverslip-buffer interface and n is the index of refraction of the buffer. Therefore, at the transverse scan position (x, 0), the retro-reflected ray from a sphere of radius R follows a path which forms an angle, ϑ, with respect to the optical axis given by Eq. (10):
| (10) |
The retro-reflected ray that follows a path that makes an angle ϑ with respect to the optical axis, travels a distance 2δ given by Eq. (11):
| (11) |
Correspondingly, the OPL = n2δ and the phase is given by:
| (12) |
Figure 4(A) shows the measured fringe visibility, m, obtained using the phase shifting algorithm (Eqs. (2) and (3)) applied at a series of discrete scan positions covering a square; the scans positions were spaced at and we used a 60x, NA =1.3 (Nikon) objective for imaging. Figure 4(B) (dotted line) shows the visibility along a single row of pixels corresponding to y = 0 and −6μm ≤ x ≤ 6μm. Correspondingly, the measured phase, γ, (via Eq. (3)) is shown in Fig. 4(C) (dotted line). Although the microscope focus is held fixed on the coverslip-buffer interface, the visibility and phase data show oscillations with a superposed envelope that decays as the scan position moves outward from the center of the sphere.
In order to fit the experimental data, we account for the variation in the density of rays with scan position because at the center of the scan, all of the incident rays contribute to the interference, but as the scan location moves off-center, fewer of the paraxial rays reflect from the sphere and re-enter the microscope objective. We introduce an angular dependent term and express the reflectivity from the sphere’s surface as: , where Bo is the fringe visibility at the center of the scan (i.e. ϑ = 0) and ϑo is a fitting parameter.
Using an initial estimate Bo = 0.038, based upon the index of refraction of the sphere and buffer as ns = 1.582 and n = 1.333, respectively and a coupling efficiency, κ = 44%, we fit the data in Figs. 4(A) and 4(B) with Eqs. (6) and (7). The fits to these data are shown in Figs. 4(A) and 4(B) (solid lines) using: A = 0.0345; ; ϑo = 25o; σ = 0.3μm; R = 7.7μm; ho = 0.005μm; n = 1.333 and λ = 0.633μm; the values for the index of refraction, n, and the wavelength, λ, were held fixed. Consequently, we can now use the values A = 0.0345 and Bo = 0.045 to refine the initial estimate of the index of refraction of the sphere. If we assume that the reflected field from the coverslip-buffer interface couples back into the laser with the same efficiency, κ, as the field that is reflected from the buffer-sphere interface, we can eliminate the dependence upon κ and we can use the ratio Bo/A to determine nsphere = 1.58.
4.3. Application of the Inverse Problem: Reconstruction of the Shape of a 15μm Diameter Sphere Using the Inverse Method
We now demonstrate the feasibility of approaching the inverse problem such that we are able to recover the shape and height of the polystyrene sphere held at a fixed distance above the coverslip-buffer interface without a priori information that we are imaging a sphere. Specifically, we wish to find the visibility and phase {B, θ} and reconstruct the shape and height of the surface above the interface from measurements of the visibility and phase {m, γ}.
Equations (8) and (9) relate the visibility and phase {B, θ} associated with the reflection from the unknown object to the measured visibility and phase {m, γ} and {A, ϕ} associated with the reflection from the coverslip-buffer interface. These two parameters may be determined by collecting visibility and phase data from the coverslip-buffer interface in the “sample-free” region where B equals zero. In this region, Eqs. (6) and (7) combined with a measurement of {m, γ} yield {A, ϕ}. With A and ϕ determined in the “sample-free” regions at the beginning and end of each scan-line, the values of {A, ϕ} in the “sample” region may be determined by interpolation.
Figure 5(A) shows the visibility, B, obtained by applying the inverse method to the raw visibility, m, and phase data, γ. Unlike the data in Fig. 4(A), however, reconstruction of the visibility using the inverse method eliminates the series of interference fringes. Because the inverse method reconstructs the visibility and phase associated with the reflection from the sample, the “sample-free” regions are shown as black. From Fig. 4(A), the measured reflectivity is highest in the center of the bead and lower towards the periphery of the scan region; this result is a consequence of the combined effect of the axial profile of the incident illumination and the curvature of the surface of the sphere. The visibility data taken from a single row of pixels corresponding to y = 0 and −6μm ≤ x ≤ 6μm in Fig. 5(A) (which corresponds to the same pixels as Fig. 4(B)) are shown in Fig. 5(B) (dotted lines). The measured OPL, calculated from Eq. (12), as a function of scan position, x, is shown in Fig. 5(C) (black squares). From the data, the height of the center of the sphere above the interface, ho, was determined to be ho = 0.005μm. The OPL data were compared to the predicted value using Eq. (11) (solid black line) and R = 7.7μm.
Fig. 5.
Inverse method used to determine the visibility and height of the surface of a sphere above an interface. (A & B) visibility and (C) δ (black squares) and height (red squares) as a function of the virtual scan position, x′ (h = h(x′)). The fit to δ (black line) and predicted height of sphere, h = h(x′) (red line) is also shown based upon a sphere with radius R = 7.7μm and ho = 0.005μm above the interface. Fit to visibility using Eq. (8) (solid line in B).
After the application of this inverse method, the phase data, θ, showed discrete phase jumps and conventional phase unwrapping algorithms were sufficient to unwrap the phase yielding the data shown in Fig. 5(B). Therefore, it was possible to reconstruct the OPL from the unwrapped phase, θ as: .
In order to verify that the inverse method reproduces the expected relationship between the height h and OPL, we compared the measured height of the sphere above the coverslip-medium interface, h, as a function of the distance from the center of the sphere, x′ with the expected value (i.e. h = h(x′)). From the geometry of Fig. 3, at the scan position, x, the shortest distance between the local tangent plane to the sphere’s surface and the coverslip-buffer interface, h, is given by Eq. (13) which is measured at a virtual location, x′, given by Eq. (14):
| (13) |
| (14) |
where ϑ and δ are given by Eqs. (10) and (11), respectively.
Figure 5(C) (red squares) shows the height of the sphere above the coverslip-medium interface, h, as a function of the distance from the center of the sphere, x′ determined using Eqs. (10)–(14). The re-mapped data were then compared to the predicted value (solid red line) for a sphere with radius, R = 7.7μm. Using h = h(x′), we compared the visibility data, m, to a prediction using Eq. (8) with with ϑo = 25o; σ = 0.3 μm (Fig. 5(B), solid line).
5. Imaging the Reflectivity and Topography of the Ventral Surface of the Cell
5.1. Reconstruction of the Visibility and Optical Path Length of Stress Fibers and Focal Adhesions
We now apply the inverse method to phase data that was acquired from a fixed MTC cell plated on glass bottom dishes. This approach reconstructs the visibility and phase associated with reflective sites near the ventral plasma membrane which lies in apposition to the coverslip-buffer interface. In order to gain insight into the location of dense, clustered sub-cellular structures and their relationship to the interference images, we used indirect immunofluorescence to image both F-actin and paxillin in a single cell (Figs. 6(A) and 6(B), respectively); the 20μm x 30μm scan region also shows black portions of the coverslip to the left of the periphery of the cell. The bright, dense sites of the adhesion-associated protein paxillin in Fig. 6(B) indicate the presence of focal adhesions [52] and the F-actin distribution in Fig. 6(A) may be interpreted as either ventral and/or dorsal stress fibers; these dense bundles of actin filaments attach to focal adhesions with the ventral fibers aligned nearly parallel to the ventral surface and the dorsal fibers aligned toward the dorsal surface with one of their ends tethered to the adhesions [53].
The application of the inverse method (Eqs. (8) and (9)) to data acquired in this 20μm x 30 μm region yields a map of the visibility (Fig. 6(C)) and the height (Fig. 6(D)), respectively. The color map in Fig. 6(C) shows that the visibilities range from 0.005 to less than 0.02 and that the majority of scan points have very low visibility. From the data in Fig. 6(C), it may be observed that in the “sample-free” region to the left of the cell, the application of Eq. (8) produces B essentially equal to zero. Ideally, Eq. (8) would yield B ≡ 0 when the scan region is on the “sample-free” region because the measured visibility, m, and phase, γ, are: m = A and γ = ϕ. It may be observed, however, that for some pixels, B ≈ 0. This deviation results from using a linear fit to the measured values of A and ϕ along an entire row of pixels rather than the precisely measured values of A and ϕ. Therefore, the small departure of B from zero in the “sample-free” region indicates that there is a small error resulting from the linear fit.
By comparison, under the cell, there are clusters of pixels with relatively high visibility and the location of these bright regions are observed to be correlated with either the regions of high F-actin density shown in Fig. 6(A) or the paxillin-dense regions shown in Fig. 6(B) or with both F-actin and paxillin.
From the visibility, it is possible to estimate the Fresnel coefficient at each scan location (assuming that the angular variations of these coefficients are negligible) and consequently the index of refraction at each pixel. Therefore, Fig. 6(C) may be interpreted as a map of the spatial variation of the index of refraction with scan position. The visibility, B, obtained from Eq. (8) is related to the coupling efficiency, κ, and the Fresnel coefficient at normal incidence, r, as B = κ|r|. In the region “sample-free” region outside the cell, Eq. (8) predicts that B = 0 at the coverslip-buffer interface. When the scan position is located beneath a region of the cell that is predominately cytoplasm (with index of refraction equal to 1.35), we expect the visibility . From the data, the majority of the pixels have an index of refraction 1.33 ≤ n ≤ 1.35, but the higher visibility pixels (those with yellow to red values on the visibility colormap), have an index of refraction such that 1.4 ≤ n ≤ 1.43.
The height map in Fig. 6(D) is determined, as explained in Section 4.1, by assuming that light propagates in a straight line from the objective through the buffer (i.e. see the geometry of Fig. S4 when the scan position is at the center of the sphere) until it was reflected from a discrete site near the ventral membrane. Therefore, the height, z, was determined from the phase, θ, as: with λ = 0.6328 μm, nb = 1.333 and f = 1.2. In the “sample-free” region, the value of θ is essentially meaningless because the visibility B should be identically zero in this region. Nevertheless, the application of Eq. (9) yields a value at each pixel in the field-of-view including the pixels in the “sample free” region. It may be observed from Fig. 6(D), that at the pixels close to the cell edge, the heights are essentially constant, but that some rows of data have a slight variation as the scan position moves to the edge of the “sample free” region. This variation results from the use of a linear fit to the measured values of A and ϕ in this region rather than the precisely measured values.
6. Visibility and Topography at the Trailing Edge of a Motile Cell
Figure 7 shows six scans of the visibility and topography (top row and bottom row, respectively) near the edge of a live cell. The data for each scan were acquired in approximately 25 seconds and the total elapsed time to acquire the six scans was approximately 40 minutes. As in Section 5.1, the data were reconstructed using the inverse method such that the visibility and topography represent the actual visibility of the cellular features and the topography represents the height of the reflective structures above the glass. Unlike the data obtained from fixed cells, however, neither paxillin nor F-actin were labeled in this cell.
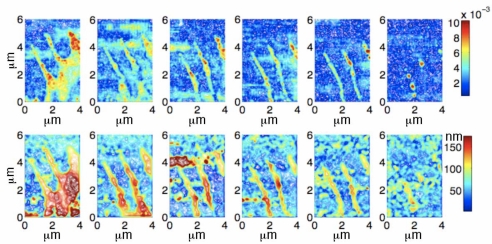
Fig. 7.
Visibility and topography reconstructed for a live cell using the inverse method. The cell may be observed to be moving towards the south-east (lower-right) of the image. Top row: six scans of the visibility. Bottom row: six scans of the topography. Each of the scans contains 60 x 40 pixels and was acquired in approximately 25 seconds. The temporal separation between scans was about 6 minutes and the total time elapsed time was approximately 40 minutes.
In each of the six data sets, the dark blue regions (essentially zero visibility) represent the glass substrate. Examination of either the visibility data (top panel) or topography, indicate that the bulk motion of the cell is toward the south-east (bottom-right) corner. The live cell data clearly demonstrate dynamic remodeling of the cytoskeleton and the dynamics of the trailing edge. In each of the first five scans, three filopodia may be observed. By the sixth scan, essentially all of the cell has disappeared from the field-of-view.
In the first scan, two filopodia appear to have approximately uniform diameter (≈ 0.5μm) and a third considerably thicker and nonuniform filopodium may be observed. Between the three filopodia of the first two scans, the edge of the cell is visible. This region has a visibility ≈ 0.006. By comparison with the fluorescence and visibility data shown in Fig. 6(A) and 6(C), the data from this edge is consistent with the thin dendritic actin network of the lamella. The visibility data from the first scan also clearly indicate the presence of highly reflective material in the filopodia (with B ≈ 0.01). In two of the three filopodia, this reflective material is most densely located at the mid-section of the shaft of the filopodia and at the base (the region where the filopodium meets the lamella), whereas the thick filopodium has very densely packed, highly reflective material throughout. Because this material has the same reflectivity as the focal adhesions in Fig. 6(C), it suggests that these regions represent the dense aggregation of actin and paxillin. The height data in these regions, ≈ 100nm above the extracellular matrix, is also consistent with the data from focal adhesions in Fig. 6(D). Therefore, on the basis of both the reflectivity and the height data, it may be concluded that these dense regions represent adhesions. Compared with the filopodia, the lamella in the first scan appears to be situated ≈ 160 nm above the matrix which is ≈ 60nm higher than the adjacent filopodia.
From the data in the first two scans, it may be observed that the transverse speed of the tips of the filopodia ( ) is much slower than the speed of the retracting lamella ( ).Although the slow retraction of the tips of the filopodia may be observed throughout the first five scans, between the fifth and sixth scan, the filopodia disappear completely from the field-of-view. By the sixth scan, only three dense, reflective regions remain; two of these regions correlate with the leftmost filopodium and the third blob correlates with the central filopodium. Comparing the location of these adhesions with the earlier scans, it may be observed that these adhesions were present at the base of the filopodia (a hint of the adhesion from the base of the third, thick filopodium may also be observed in the sixth scan).
7. Discussion
We have coupled phase-shifted laser feedback interferometry with an inverted microscope so as to measure the change in phase and amplitude of the electric field upon reflection from discrete sites near the ventral plasma membrane when the cell was imaged through a glass coverslip. Combined with the experimental implementation, we have applied a solution to the forward problem appropriate to our imaging geometry so that we were able to compare model predictions with the measured phase change near focus and with the reflectivity and phase of the field reflected from a calibration sphere. In addition, we have developed an algorithm that addresses the inverse problem so that we can separate the contribution of the reflection from the coverslip-buffer interface from the field that has been elastically scattered by sub-cellular structures.
Using this approach, we have reconstructed the topography and reflectivity of regions of the ventral membrane at focal adhesions. As expected, there is a strong correlation between the presence of paxillin and actin in stress fibers (as identified with fluorescence imaging) and the interference images. Unlike the data obtained with RICM, which show dark regions at focal adhesions [1–4], using psLFIM we are able to demonstrate that these optically dense regions on the cytoplasmic face have high reflectivity and we are able to measure the topography of the regions independently of the reflectivity. The data clearly demonstrate that the majority of the highly reflective regions are closer to the coverslip than the less reflective regions.
Although psLFIM offers a high precision measurement of the phase and reflectivity (limited by photon counting statistics), an accurate determination of sample topography and index of refraction depends upon several model assumptions. In order to interpret our interference data, we have assumed that the electric field collected by the microscope objective consists of a reflection of the incident electric field from the coverslip-buffer interface and an additional, single reflection from a discrete, protein dense, site near the ventral plasma membrane. Alternatively, it is possible to incorporate a model that stipulates reflection from a series of discrete layers of known index of refraction [54].
Because we have assumed reflection from a single discrete layer, we are able to apply this model to the measured fringe visibility and phase and determine the index of refraction and the optical path length (topography) at each pixel. From the measured data, we are able to determine the distance between the coverslip-buffer interface and the adhesion. This interpretation relies on an assumption that actin filaments and the protein plaque are quite dense such that the backscattered photons reflect from the surface of the adhesion.
Assuming a homogeneous index of refraction for the cytoplasm that is essentially equal to the index of refraction of the buffer, the reflectivity data indicate that the majority of pixels near the ventral plasma membrane have an index of refraction that is close to the index of the cytoplasm, but that the index of refraction of sub-cellular sites in focal adhesions have an index greater than 1.4. Although this is a precise estimate and the higher index of refraction is consistent with measured values from lipid and organelles like mitochondria [55], the accuracy of this measurement depends upon knowledge of the index of refraction of the cytoplasm (generally assumed to be ≈ 1.35 [54]) and the validity of the model.
Furthermore, in order to interpret the reflectivity data at each pixel, we have assumed that the incident, linearly polarized light is not significantly depolarized as it undergoes a single reflection from discrete sites within the focal adhesions. This assumption is consistent with observations of scattering from cells which demonstrated that the dominate sub-cellular features that backscatter light, organelles with sizes between ≈ λ/4–λ/2 (e.g. peroxisomes, lysosomes and mitochondria), do not depolarize the linearly polarized incident light [55–57]. Our data suggest that this assumption is justified.
Recently, the fluorescence based, super-resolution technique ”interferometric photoactivated localization microscopy (iPALM) [58]” has been applied to determine the stratification of protein topography within a focal adhesion [59]; this technique offers transverse resolution below the diffraction limit [13] and the axial position of the fluorescence protein is determined interferometrically. Based upon images obtained from fixed human osteosarcoma (U2OS) and mouse embryonic fibroblast (MEF) cells on fibronectin-coated glass, the data suggest that the adapter proteins within the adhesion (e.g. paxillin and vinculin) reside in a thin layer that is ≈ 40 nm above the coverslip. By contrast, this method demonstrates that within the focal adhesion actin is located within a relatively thick layer of width ≈ 15 nm at a mean height of ≈ 96nm above the coverslip. The data from these experiments suggest that the topography that we have measured within the focal adhesion, Fig. 6(D), predominately represents the height of the actin layer (≈ 100 nm) above the coverslip. Therefore, we conclude that the majority of the elastically scattered photons that contribute to the most reflective structures in Fig. 6(C) are reflected from F-actin rather than from a thin layer of paxillin.
As shown in Fig. 7, the technique may be used to image live, motile cells. The data demonstrate that both the visibility and topography may be determined as the cell rapidly remodels. As with other imaging techniques, the speed of the measurements (pixel dwell time) is limited by the desired signal-to-noise ratio and by the Nyquist sampling criterion. Because the precision of a phase measurement increases as the number of collected photons increases, increasing the pixel dwell time will increase the precision. Conversely, rapid motion may lead to blur and decrease in signal-to-noise caused by reduce fringe visibility. Previously, we have demonstrated that the precision of a phase measurement decreases as the fringe visibility decreases and that when the fringe visibility is 0.01, the random error in the height measurement was measured to be approximately 1 nm, but the error increases to 10 nm when the visibility equals 0.001 [30].
Currently, all of the phase calculations are done on-the-fly and written to screen and plotted. There is considerable computational overhead associated with this approach, but it allows the user to monitor aspects of the scan. Alternatively, it is possible to implement code that does not plot any data as it is acquired. This is approach, coupled with optimal memory management of the acquired data, would be faster. Because the total scan time depends upon both the pixel dwell and the number of pixels in the scan, there is always a compromise in choosing the pixel step size. In order to avoid aliasing, the step size is chosen so as match the effective point spread function. Because of experimental noise, however, it is important to sample even faster than the Nyquist sampling frequency. The chosen step size therefore depends upon the nature of the rate of change of the measured phase, the signal-to-noise ratio and the requisite dwell-time. One approach is to implement a coarse scan in order to determine gross changes and then a finer scan with smaller step-sizes.
Applying psLFIM to a live cell can yield data that is extremely difficult to obtain using fluorescent imaging methods such as total internal fluorescence microscopy. In particular, the data obtained from the motile cell in Fig. 7 may be used to gain insight into the physiological mechanisms that govern the retraction of filopodia. Both the reflectivity and topography data (Figs. 7 top and bottom rows, respectively) suggest that there are adhesions at the tip, shaft and base of the two uniform filopodia and this conclusion is consistent with the observations of three distinct type of adhesions that have been found in the filopodium of sensory growth cones [60]. These three adhesions types have unique functions in filopodium dynamics. In particular, it has been shown that: (1) tip adhesions provide guidance cues that govern filopodium movements; (2) shaft adhesions control the dynamics of the dendritic actin network that constitutes the lamella (termed a veil) and (3) basal adhesions affect filopodium dynamics. In the retracting filopodia observed in Fig. 7, the tip adhesions appear quite weak whereas the basal adhesions appear firmly anchored to the extracellular matrix such that they are ultimately left behind (in the sixth scan) as the cell leaves the field-of-view. The extended lifetime of these basal adhesions is completely consistent with previous observations [60]. The reflectivity and topography data associated with the thick filopodium is consistent with previous observations in growth cones that suggest that thickened filopodia support strong adhesions, while the uniform and even margins associated with the other two filopodia are consistent with previous observations associated with moving filopodia. The rapid retraction of the veil region observed between the first and second scan indicate that the veil clearly does not adhere to the extracellular matrix. This observation is consistent with both the reflectivity and topography data obtained from the veil region; the reflectivity data demonstrate the reduced optical density of the dendritic network as compared with adhesive regions and the topography data indicate that the veil is nearly 50 nm above the adhesive regions. Finally, the data obtained from these dynamic filopodia suggest that retrograde flow is the dominate mechanism responsible for retraction although disassembly at the tip likely contributes [61–64].
Live cells can exhibit a range of motion, from extremely rapid to essentially stationary in the field-of-view. Therefore, the applicability of this method depends both upon the rate of change of the phase at a given pixel and the rate of change of the phase between adjacent pixels. As with other forms of interferometry, for large changes in optical path length, if the phase is under-sampled, it will not be possible to successfully unwrap the 2π phase changes should these occur. Because the laser feedback interferometer has been demonstrated to respond linearly and without distortion to dynamic changes in the optical path length until about 1 MHz [30], it should be possible to use this approach to measure thermally and actively driven membrane fluctuations and dynamic changes in cell shape and organelles, an area where the application of RICM has been used extensively; it has been observed that these thermally driven membrane fluctuations at physiological temperatures are of order 10 nm rms with a wavelength ≤ 0.5 μm [65].
Alternatively, rather than image large changes in optical path length, psLFIM should be an ideal method for studying the earliest phases in the birth of integrin adhesions. In particular, we plan to apply the method in order to verify the predictions of a model that we have developed that provides a mechanistic understanding of the processes that govern the earliest integrin adhesions [66]. In analogy with the cellular measurements presented in Ref. [67] and the measurements on vesicles decorated with receptor and/or repeller molecules [68–72], the sensitivity of psLFIM to static and dynamic changes in the actin network should permit its applicability to the measurement of the nucleation, dissolution and merging of integrin adhesions at the ventral surface of cells on glass substrates.
8. Conclusion
We have coupled phase-shifted laser feedback interferometry with an inverted microscope and developed and verified the accuracy of an algorithm that addresses the inverse problem so that we can separate the contribution of the reflection from the coverslip-buffer interface from the field that has been elastically scattered by sub-cellular structures. Using this approach, we have reconstructed the topography and reflectivity of regions of the ventral membrane at focal adhesions. As expected, there is a strong correlation between the presence of paxillin and actin in stress fibers as identified with fluorescence imaging) and the interference images. Unlike the data obtained with RICM, which show dark regions at focal adhesions, using psLFIM we are able to demonstrate that these optically dense regions on the cytoplasmic face have high reflectivity and we are able to measure the topography of the regions independently of the reflectivity. The data acquired from fixed and live cells show the presence of a dense actin layer located ≈ 100 nm above the coverslip interface. Additionally, the measured dynamics of filopodia and the lamella in a live cell supports retrograde flow as the dominate mechanism responsible for filopodia retraction.
Acknowledgments
We thank Amber L. Wells for help with the tissue culture. This work was supported by a grant from the National Institutes of Health: R01GM076293 (B.O.).
References and links
- 1.Curtis A. S. G., “The mechanism of adhesion of cells to glass. A study by interference reflection microscopy,” J. Cell Biol. 20(2), 199–215 (1964). 10.1083/jcb.20.2.199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Verschueren H., “Interference reflection microscopy in cell biology: Methodology and applications,” J. Cell Sci. 75(1), 279–301 (1985). [DOI] [PubMed] [Google Scholar]
- 3.Weber I., “Reflection interference contrast microscopy,” Meth. Enzymol. 361, 34–47 (2003). 10.1016/S0076-6879(03)61004-9 [DOI] [PubMed] [Google Scholar]
- 4.Izzard C., Lochner L., “Cell-to-substrate contacts in living fibroblasts: an interference reflexion study with an evaluation of the technique,” J. Cell Sci. 21, 129–159 (1976). [DOI] [PubMed] [Google Scholar]
- 5.Radler J., Sackmann E., “On the measurement of weak repulsive and frictional colloidal forces by reflection interference contrast microscopy,” Langmuir 8(3), 848–853 (1992). 10.1021/la00039a019 [DOI] [Google Scholar]
- 6.Smith A. S., Sackmann E., “Progress in mimetic studies of cell adhesion and the mechanosensing,” ChemPhysChem 10(1), 66–78 (2009). 10.1002/cphc.200800683 [DOI] [PubMed] [Google Scholar]
- 7.Limozin L., Sengupta K., “Quantitative reflection interference contrast microscopy (RICM) in soft matter and cell adhesion,” ChemPhysChem 10(16), 2752–2768 (2009). 10.1002/cphc.200900601 [DOI] [PubMed] [Google Scholar]
- 8.Salaita K., Nair P. M., Petit R. S., Neve R. M., Das D., Gray J. W., Groves J. T., “Restriction of receptor movement alters cellular response: physical force sensing by EphA2,” Science 327(5971), 1380–1385 (2010). 10.1126/science.1181729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Iwanaga Y., Braun Y. D., Fromherz P., “No correlation of focal contacts and close adhesion by comparing GFP-vinculin and fluorescence interference of DiI,” Eur. Biophys. J. 30(1), 17–26 (2001). 10.1007/s002490000119 [DOI] [PubMed] [Google Scholar]
- 10.Parthasarathy R., Groves J. T., “Optical techniques for imaging membrane topography,” Cell. Biochem. Biophys. 1(3), 391–414 (2004). 10.1385/CBB:41:3:391 [DOI] [PubMed] [Google Scholar]
- 11.Groves J. T., Parthasarathy R., Forstner M. B., “Fluorescence imaging of membrane dynamics,” Annu. Rev. Biomed. Eng. 10, 311–338 (2008). 10.1146/annurev.bioeng.10.061807.160431 [DOI] [PubMed] [Google Scholar]
- 12.Ganesan P. V., Boxer S. G., “A membrane interferometer,” Proc. Nat. Acad. Sci. U.S.A. 106(14), 5627–5632 (2009). 10.1073/pnas.0901770106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313(5793), 1642–1645 (2006). 10.1126/science.1127344 [DOI] [PubMed] [Google Scholar]
- 14.Shroff H., Galbraith C. G., Galbraith J. A., White H., Gillette J., Olenych S., Davidson M. W., Betzig E., “Dual-color superresolution imaging of genetically expressed probes within individual adhesion complexes,” Proc. Nat. Acad. Sci. U.S.A. 104(51), 20308–20313 (2007). 10.1073/pnas.0710517105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shroff G., Hari C. G, Betzig E., “Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics,” Nat. Meth. 5, 417–423 (2008). 10.1038/nmeth.1202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gauglitz G., Proll G., “Strategies for label-free optical detection,” Adv. Biochem. Eng. Biotech. 109, 395–432 (2008). [DOI] [PubMed] [Google Scholar]
- 17.Bornhop D. J., Latham J. C., Kussrow A., Markov D. A., Jones R. D., Sorensen H. S., “Free-solution, label-free molecular interactions studied by back-scattering interferometry,” Science 317(5845), 1732 (2007). 10.1126/science.1146559 [DOI] [PubMed] [Google Scholar]
- 18.Ovryn B., “Three-dimensional forward scattering particle image velocimetry applied to a microscopic field-of-view,” Exp. Fluids 29(1), S175–S184 (2000). 10.1007/s003480070019 [DOI] [Google Scholar]
- 19.Ding H., Millet L. J., Gillette M. U., Popescu G., “Actin-driven cell dynamics probed by Fourier transform light scattering,” Biomed. Opt. Express 1(1), 260–267 (2010). 10.1364/BOE.1.000260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ding H. F., Wang Z., Nguyen F., Boppart S. A., Popescu G., “Fourier transform light scattering of inhomogeneous and dynamic structures,” Phys. Rev. Lett. 101(23), 238102 (2008). 10.1103/PhysRevLett.101.238102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shaked N. T., Zhu Y., Rinehart M. T., Wax A., “Two-step-only phase-shifting interferometry with optimized detector bandwidth for microscopy of live cells,” Opt. Express 17(18), 15585–15591 (2009) 10.1364/OE.17.015585 [DOI] [PubMed] [Google Scholar]
- 22.Shaked N. T., Satterwhite L. L., Bursac N., Wax A, “Whole-cell-analysis of live cardiomyocytes using wide-field interferometric phase microscopy,” Biomed. Opt. Express 1(2), 706–719 (2010) 10.1364/BOE.1.000706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang C. H., Lin J. Y., Lee C. H., “Membrane ripples of a living cell measured by non-interferometric wide-field optical profilometry,” Opt. Express 13(26), 10665–10672 (2005). 10.1364/OPEX.13.010665 [DOI] [PubMed] [Google Scholar]
- 24.Chen C. H., Tsai F. C., Wang C. C., Lee C. H., “Three-dimensional characterization of active membrane waves on living cells,” Phys. Rev. Lett. 103 238101 (2009). 10.1103/PhysRevLett.103.238101 [DOI] [PubMed] [Google Scholar]
- 25.Sheppard C. J. R., Roy M., Sharma M. D., “Image formation in low-coherence and confocal interference microscopes,” Appl. Opt. 43(7), 1493–1502 (2004). 10.1364/AO.43.001493 [DOI] [PubMed] [Google Scholar]
- 26.Peek T. H., Bolwijn P. T., Alkemade C. T. J., “Axial mode number of gas lasers from moving-mirror experiments,” Am. J. Phys. 35(9), 820–831 (1967). 10.1119/1.1974260 [DOI] [Google Scholar]
- 27.Bearden A., O’Neill M. P., Osborne L. C., Wong T. L., “Imaging and vibrational analysis with laser-feedback interferometry,” Opt. Lett. 18(3), 238–240 (1993). 10.1364/OL.18.000238 [DOI] [PubMed] [Google Scholar]
- 28.Juskaitis R., Rea N., Wilson T., “Fibre-optic based confocal microscopy using laser detection,” Opt. Commun. 99(1), 105–113 (1993). 10.1016/0030-4018(93)90713-F [DOI] [Google Scholar]
- 29.Ovryn B., Andrews J. H., “Phase-shifted laser feedback interferometry,” Opt. Lett. 23(14), 1078–1080 (1998). 10.1364/OL.23.001078 [DOI] [PubMed] [Google Scholar]
- 30.Ovryn B., Andrews J. H., “Measurement of changes in optical path length and reflectivity with phase-shifting laser feedback interferometry,” Appl. Opt. 38(10), 1959–1967 (1999). 10.1364/AO.38.001959 [DOI] [PubMed] [Google Scholar]
- 31.Atilgan E., Ovryn B., “Membrane deformation at integrin adhesions,” Curr. Pharma. Biotechnol. 10(5), 508–514 (2009). 10.2174/138920109788922146 [DOI] [PubMed] [Google Scholar]
- 32.Wolfenson H., Henis Y. I., Geiger B., Bershadsky A. D., “The heel and toe of the cells foot: a multifaceted approach for understanding the structure and dynamics of focal adhesions,” Cell Motil. Cytoskeleton. 66(11), 1017–1029 (2009). 10.1002/cm.20410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dubash A. D., Menold M. M., Samson T., Boulter E., Garcia-Mata R., Doughman R., Burridge K., “Focal adhesions: new angles on an old structure,” Int. Rev. Cell Mol. Biol. 277, 1–65 (2009). 10.1016/S1937-6448(09)77001-7 [DOI] [PubMed] [Google Scholar]
- 34.Keller J. B., “Inverse problems,” A. Math. Mon. 83(2), 107–118 (1976). 10.2307/2976988 [DOI] [Google Scholar]
- 35.Radler J J., Sackmann E., “Imaging optical thicknesses and separation distances of phospholipid vesicles at solid surfaces,” J. Phys. II France 3(5), 727–748 (1993). 10.1051/jp2:1993163 [DOI] [Google Scholar]
- 36.Clack N. G., Groves J. T., “Many-particle tracking with nanometer resolution in three dimensions by reflection interference contrast microscopy,” Langmuir 21(14), 6430–6435 (2005). 10.1021/la050372r [DOI] [PubMed] [Google Scholar]
- 37.Singer I. I., Scott S., Kawka D. W., Kazazis D. M., Gailit J., Ruoslahti E., “Cell surface distribution of fibronectin and vitronectin receptors depends on substrate composition and extracellular matrix accumulation.” J. Cell Biol. 106(6), 2171–2182 (1988). 10.1083/jcb.106.6.2171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ma X., Lu J.Q., Brock R. S., Jacobs K. M., Hu X.H., “Determination of complex refractive index of polystyrene microspheres from 370 to 1610 nm,” Phys. Med. Biol. 48(24), 4165–4172 (2003). 10.1088/0031-9155/48/24/013 [DOI] [PubMed] [Google Scholar]
- 39.Wang W., Wycko J. B., Frohlich V. C., Oleynikov Y., Huttelmaier S., Zavadil J., Cermak L., Bottinger E. P., Singer R. H., White J. G., Segall J. E., Condeelis J. S., “Single cell behavior in metastatic primary mammary tumors correlated with gene expression patterns revealed by molecular profiling,” Cancer Res. 62, 6278–6288 (2002). [PubMed] [Google Scholar]
- 40.Nicolson G. L., “Differential organ tissue adhesion, invasion, and growth properties of metastatic rat mammary adenocarcinoma cells,” Breast Cancer Res. Treat. 12(2), 167–176 (1988). 10.1007/BF01805938 [DOI] [PubMed] [Google Scholar]
- 41.Hariharan P., Oreb B. F., Eiju T., “Digital phase-shifting interferometry: a simple error-compensating phase calculation algorithm,” Appl. Opt. 26(13), 2504–2506 (1987). 10.1364/AO.26.002504 [DOI] [PubMed] [Google Scholar]
- 42.Creath K., “Phase measurement interferometry techniques,” in Progress in Optics, Wolf E. eds. (North-Holland, 1988) XXVI 349–393 10.1016/S0079-6638(08)70178-1 [DOI] [Google Scholar]
- 43.Cheng Y. Y., Wyant J. C., “Two-wavelength phase shifting interferometry,” Appl. Oct. 23(24), 4539–4543 (1984). 10.1364/AO.23.004539 [DOI] [PubMed] [Google Scholar]
- 44.Born M., Wolf E., Principles of Optics (Cambridge University Press, 1998). [Google Scholar]
- 45.Sheppard G. J. R., Matthews H. J., “Imaging in high-aperture optical systems,” J. Opt. Soc. Am. A 4(8), 1354–1360 (1987). 10.1364/JOSAA.4.001354 [DOI] [Google Scholar]
- 46.Hess S. T., Webb W. W., “Focal volume optics and experimental artifacts in confocal fluorescence correlation spectroscopy,” Biophys. J. 83(4), 2300–2317 (2002). 10.1016/S0006-3495(02)73990-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sheppard C. J. R., Larkin K. G., “Effect of numerical aperture on interference fringe spacing,” Appl. Opt. 34(22), 4731–4734 (1995). 10.1364/AO.34.004731 [DOI] [PubMed] [Google Scholar]
- 48.Hwang J., Moerner W., “Interferometry of a single nanoparticle using the Gouy phase of a focused laser beam,” Opt. Commun. 280(2), 487–491 (2007). 10.1016/j.optcom.2007.08.032 [DOI] [Google Scholar]
- 49.Renhorn I. G. E., Boreman G. D., “Analytical fitting model for rough-surface BRDF,” Opt. Express 16(17), 12892–12898 (2008). 10.1364/OE.16.012892 [DOI] [PubMed] [Google Scholar]
- 50.He X. D., Torrance K. E., Sillion F. X., Greenberg D. P., “A comprehensive physical model for light reflection,” SIGGRAPH Comput. Graph. 25(4), 175–186 (1991). 10.1145/127719.122738 [DOI] [Google Scholar]
- 51.Fischer D. G., Ovryn B., “Interfacial shape and contact-angle measurement of transparent samples with confocal interference microscopy,” Opt. Lett. 25(7), 478–480 (2000). 10.1364/OL.25.000478 [DOI] [PubMed] [Google Scholar]
- 52.Mitra S. K., Hanson D. A., Schlaepfer D. D., “Focal adhesion kinase: in command and control of cell motility,” Nat. Rev. Mol. Cell Biol. 6(1), 56–68 (2005). 10.1038/nrm1549 [DOI] [PubMed] [Google Scholar]
- 53.Pellegrin S., Mellor H., “Actin stress fibres,” J. Cell Sci. 120(20), 3491–3499 (2007). 10.1242/jcs.018473 [DOI] [PubMed] [Google Scholar]
- 54.Bailey J., Gingell D., “Contacts of chick fibroblasts on glass: results and limitations of quantitative interferometry,” J. Cell Sci. 90(2), 215–224 (1988). [DOI] [PubMed] [Google Scholar]
- 55.Mourant J. R., Johnson T. M., Freyer J. P., “Characterizing mammalian cells and cell phantoms by polarized backscattering fiber-optic measurements,” Appl. Opt. 40(28), 5114–5123 (2001). 10.1364/AO.40.005114 [DOI] [PubMed] [Google Scholar]
- 56.Schmitt J. M., Kumar G. , “Optical scattering properties of soft tissue: a discrete particle model,” Appl. Opt. 37(13), 2788–2797 (1998). 10.1364/AO.37.002788 [DOI] [PubMed] [Google Scholar]
- 57.Rueckel M., Denk W., “Properties of coherence-gated wavefront sensing,” J. Opt. Soc. Am. A 24(11), 3517–3529 (2007). 10.1364/JOSAA.24.003517 [DOI] [PubMed] [Google Scholar]
- 58.Shtengel G., Galbraith J. A., Galbraith C. G., Lippincott-Schwartz J., Gillette J. M., Manley S., Sougrat R., Waterman C. M., Kanchanawong P., Davidson M. W., Fetter R. D., Hess H. F., “Interferometric fluorescent super-resolution microscopy resolves 3D cellular ultrastructure,” Proc. Nat. Acad. Sci. U.S.A. 106(9), 3125–3130 (2009). 10.1073/pnas.0813131106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kanchanawong P., Shtengel G., Pasapera A. M. G., Ramko E. B, Davidson M. W., Hess H. F., Waterman C. M., “Nanoscale architecture of integrin-based cell adhesions,” Nature 468(7323), 580–584 (2010). 10.1038/nature09621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Steketee M. B., Tosney K. W., “Three functionally distinct adhesions in filopodia: shaft adhesions control Lamellar extension,” J. Neurol. 22(18), 8071–8083 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mallavarapu A., Mitchison T. J., “Regulated actin cytoskeleton assembly at filopodium tips controls their extension and retraction,” Cell Biol. 146(5), 1097–1106 (1999). 10.1083/jcb.146.5.1097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Le Clainche C., Carlier M. F., “Regulation of actin assembly associated with protrusion and adhesion in cell migration,” Physiol. Rev. 88(2), 489–513 (2008). 10.1152/physrev.00021.2007 [DOI] [PubMed] [Google Scholar]
- 63.Geiger B., Spatz J. P., Bershadsky A. D., “Environmental sensing through focal adhesions,” Nat. Rev. Mol. Cell Biol. 10(1), 21–33 (2009). 10.1038/nrm2593 [DOI] [PubMed] [Google Scholar]
- 64.Mattila P. K., Lappalainen P., “Filopodia: molecular architecture and cellular functions,” Nat. Rev. Mol. Cell Biol. 9, 446–454 (2008). 10.1038/nrm2406 [DOI] [PubMed] [Google Scholar]
- 65.Zidovska A., Sackmann E., “Brownian Motion of nucleated cell envelopes impedes adhesion,” Phys. Rev. Lett. 96, 048103 (2006). 10.1103/PhysRevLett.96.048103 [DOI] [PubMed] [Google Scholar]
- 66.Atilgan E., Ovryn B., “Nucleation and growth of integrin adhesions,” Biophys. J. 96, 3555–3572 (2009). 10.1016/j.bpj.2009.02.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Pierres A. A. M., Benoliel D., Touchard D., Bongrand P., “How cells tiptoe on adhesive surfaces before sticking,” Biophys. J. 94, 4114–4122 (2008). 10.1529/biophysj.107.125278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Limozin L., Sengupta K., “Modulation of vesicle adhesion and spreading kinetics by Hyaluronan cushions,” Biophys. J. 93, 3300–3313 (2007). 10.1529/biophysj.107.105544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Boulbitch A., Guttenberg Z., Sackmann E., “Kinetics of membrane adhesion mediated by Ligand-receptor interaction studied with a biomimetic system,” Biophys. J. 81, 2743–2751 (2007). 10.1016/S0006-3495(01)75917-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Radler J. O., Feder T. J., Strey H. H., Sackmann E., “Fluctuation analysis of tension-controlled undulation forces between giant vesicles and solid substrates,” Phys. Rev. E 51, 4526–4536 (1995). 10.1103/PhysRevE.51.4526 [DOI] [PubMed] [Google Scholar]
- 71.Zuckerman D., Bruinsma R., “Vesicle-vesicle adhesion by mobile lock-and-key molecules: Debye-Huckel theory and Monte Carlo simulation,” Phys. Rev. E 57, 964–977 (1998). 10.1103/PhysRevE.57.964 [DOI] [Google Scholar]
- 72.Smith A. S., Sengupta K., Goennenwein S., Seifert U., Sackmann E., “Force-induced growth of adhesion domains is controlled by receptor mobility,” Proc. Nat. Acad. Sci. U.S.A. 105, 6906–6911 (2008). 10.1073/pnas.0801706105 [DOI] [PMC free article] [PubMed] [Google Scholar]